数据结构与算法 - B树
一、概述
1. 历史
B树(B-Tree)结构是一种高效存储和查询数据的方法,它的历史可以追溯到1970年代早期。B树的发明人Rudolf Bayer和Edward M. McCreight分别发表了一篇论文介绍了B树。这篇论文是1972年发表于《ACM Transactions on Database Systems》中的,题目为“Organization and Maintenance of Large Ordered Indexes”。
这篇论文提出了一种能够高效地维护大型有序索引的方法,这种方法的主要思想是将每个节点扩展成多个子节点,以减少查找所需的次数。B树结构非常适合应用于磁盘等大型存储器的高效操作,被广泛应用于关系数据库和文件系统中。
B树结构有很多变种和升级版,例如B+树、B*树和SB树等。这些变种和升级版本都基于B树的核心思想,通过调整B树的参数和结构,提高了B树在不同场景下的性能表现。
总的来说,B树结构是一个非常重要的数据结构,为高效存储和查询大量数据提供了可靠的方法。它的历史可以追溯到上个世纪70年代,而且在今天仍然被广泛应用于各种场景。
2. B的含义
B树的名称是由其发明者Rudolf Bayer提出的。Bayer和McCreight从未解释B代表什么,人们提出了许多可能的解释,比如Boeing、balance、between、broad、bushy和Bayer等。但McCreight表示,越是思考B-trees中的B代表什么,就越能更好地理解B-trees。
3. 特性
一棵B-树具有以下性质
特性1:每个节点x具有
- 属性n,表示节点x中key的个数
- 属性leaf,表示节点是否是叶子节点
- 节点key可以有多个,以升序存储
特性2:每个非叶子节点中的孩子数是n + 1、叶子节点没有孩子
特性3:最小度数t(节点的孩子数称为度)和节点中键数量的关系如下:
| 最小度数t | 键数量范围 |
|---|---|
| 2 | 1 ~ 3 |
| 3 | 2 ~ 5 |
| 4 | 3 ~ 7 |
| ... | ... |
| n | (n-1) ~ (2n-1) |
其中,当节点中键数量达到其最大值时,即3、5、7··· 2n - 1,需要分裂
特性4:叶子节点的深度都相同
问题1:B-树为什么有最小度数的限制?
答:B树种有最小度数的限制是为了保证B树的平衡特性。
在B树中,每个节点都可以有多个子节点,这使得B树可以存储大量的键值,但也带来了一些问题。如果节点的子节点数量太少,那么就可能导致B树的高度过高,从而降低了B树的效率。此外,如果节点的子节点数量太多,那么就可能导致节点的搜索、插入和删除操作变得复杂和低效。
最小度数的限制通过限制节点的子节点数量,来平衡这些问题。在B树种,每个节点的子节点数量都必须在一定的范围内,即t到2t之间(其中t为最小度数)
4. B-树与2-3树、2-3-4树的关系
可以这样总计它们之间的关系:
- 2-3树是最小度数为2的B树,其中每个节点可以包含2个或3个子节点
- 2-3-4树是最小度数为2的B树的一种特殊情况,其中每个节点可以包含2个、3个或4个子节点
- B树是一种更加一般化的平衡树,可以适应不同的应用场景,其节点可以包含任意数量的键值,节点的度数取决于最小度数t的设定。
二、实现
1. 定义节点
static class Node {boolean leaf = true;int keyNumber;int t;int[] keys;Node[] children; public Node(int t) {this.t = t;this.keys = new int[2 * t - 1];this.children = new Node[2 * t];}@Overridepublic String toString() {return Arrays.toString(Arrays.copyOfRange(keys, 0, keyNumber));}
}- leaf表示是否是叶子节点
- keyNumber为keys中有效key数目
- t为最小度数,它决定了节点中key的最小、最大数目,分别是t - 1 和 2t - 1
- keys存储此节点的key
- children存储此节点的child
- toString只是为了方便调试和测试,非必须
- 实际keys应当改为entries以便同时保存key和value,刚开始简化实现
2. 多路查找
为上面节点添加get方法
/*** 多路查找* @param key* @return*/public Node get(int key) {int i = 0;while(i < keyNumber) {if(keys[i] == key) {return this;}if(keys[i] > key) {break;}i++;}// 执行到此时,keys[i] > key 或 i==keyNumberif(leaf) {return null;}// 非叶子节点情况return children[i].get(key);}3. 插入key和child
为上面节点类添加insertKey和insertChild方法
/*** 向keys指定索引处插入key* @param key* @param index*/public void insertKey(int key, int index) {System.arraycopy(keys, index, keys, index + 1, keyNumber - index);keys[index] = key;keyNumber++;}/*** 向children指定索引处插入child* @param child* @param index*/public void insertChild(Node child, int index) {System.arraycopy(children, index, children, index + 1, keyNumber - index);children[index] = child;}作用是向keys数组或children数组指定index处插入新数据,注意
①由于使用了静态数组,并且不会在新增或删除时改变它的大小,因此需要额外的keyNumber来指定数组内有效key的数目
- 插入时keyNumber++
- 删除时减少keyNumber的值即可
②children不会单独维护数目,它比keys多一个
③如果这两个方法同时调用,注意它们的先后顺序,insertChild后调用,因为它计算复制元素时用到了keyNumber
4. 定义树
public class BTree {final int t;final int MIN_KEY_NUMBER;final int MAX_KEY_NUMBER;Node root;public BTree() {this(2);}public BTree(int t) {this.t = t;MIN_KEY_NUMBER = t - 1;MAX_KEY_NUMBER = 2 * t - 1;root = new Node(t);}
}5. 插入
/*** 新增* @param key*/public void put(int key) {doPut(root, key, null, 0);}private void doPut(Node node, int key, Node parent, int index) {// 1. 查找本节点的插入位置iint i = 0;while(i < node.keyNumber) {if(node.keys[i] == key) {// 更新return;}if(node.keys[i] > key) {break; // 找到插入位置,即为此时的i}i++;}// 2. 如果节点是叶子节点,可以直接插入了if(node.leaf) {node.insertKey(key, i);// 上限}// 3. 如果节点是非叶子节点,需要在children[i]处继续递归插入else {doPut(node.children[i], key, node, i);// 上限}if(isFull(node)) {split(node, parent, index);}}boolean isFull(Node node) {return node.keyNumber == MAX_KEY_NUMBER;}首先查找本节点中的插入位置i,如果没有空位(key被找到),应该走更新的逻辑,目前什么没做
接下来分两种情况:
- 如果节点是叶子节点,可以直接插入了
- 如果节点是非叶子节点,需要在children[i]处继续递归插入
无论哪种情况,插入完成后都可能超过节点keys数目限制,此时应当执行节点分裂
- 参数中的parent和index都是给分裂方法用的,代表当前节点父节点,和分裂节点都是第几个孩子
判断依据为:
boolean isFull(Node node) {return node.keyNumber == MAX_KEY_NUMBER;
}6. 分裂
/*** 分裂* @param left 要分裂的节点* @param parent 分裂节点的父节点* @param index 分裂节点是第几个孩子*/private void split(Node left, Node parent, int index) {// 分裂节点为根节点if(parent == null) {Node newRoot = new Node(t);newRoot.leaf = false;newRoot.insertChild(left, 0);this.root = newRoot;parent = newRoot;}// 1. 创建right节点,把left节点中t之后的key和child移动过去Node right = new Node(t);// 新增节点是否是叶子节点与待分裂节点一致right.leaf = left.leaf;System.arraycopy(left.keys, t, right.keys, 0, t - 1);// 如果分裂节点为非叶子节点if(!left.leaf) {System.arraycopy(left.children, t, right.children, 0, t);}right.keyNumber = t - 1;left.keyNumber = t - 1;// 2. 中间的key(t - 1处)插入到父节点int mid = left.keys[t - 1];parent.insertKey(mid, index);// 3. right节点作为父节点的孩子parent.insertChild(right, index + 1);}分为两种情况:
①如果parent == null,表示要分裂的是根节点,此时需要创建新根,原来的根节点作为新根的0孩子
②否则
- 创建right节点(分裂后大于当前left节点的)把t以后的key和child都拷贝过去
- t - 1处的key插入到parent的index处,index指left作为孩子时的索引
- right节点作为parent的孩子插入到index+1处
7. 删除
case 1:当前节点是叶子节点,没找到
case 2:当前节点是叶子节点,找到了
case 3:当前节点是非叶子节点,没找到
case 4:当前节点是非叶子节点,找到了
case 5:删除后key数目 < 下限(不平衡)
case 6:根节点
Node节点类添加一些方法:
/*** 向keys指定索引处插入key* @param key* @param index*/public void insertKey(int key, int index) {System.arraycopy(keys, index, keys, index + 1, keyNumber - index);keys[index] = key;keyNumber++;}/*** 向children指定索引处插入child* @param child* @param index*/public void insertChild(Node child, int index) {System.arraycopy(children, index, children, index + 1, keyNumber - index);children[index] = child;}/*** 移除指定index处的key* @param index* @return*/int removeKey(int index) {int t = keys[index];System.arraycopy(keys, index + 1, keys, index, --keyNumber - index);return t;}/*** 移除最左边的key* @return*/public int removeLeftmostKey() {return removeKey(0);}/*** 移除最右边的key* @return*/public int removeRightmostKey() {return removeKey(keyNumber - 1);}/*** 移除指定index处的child* @param index* @return*/public Node removeChild(int index) {Node t = children[index];System.arraycopy(children, index + 1, children, index, keyNumber - index);children[keyNumber] = null; // help GCreturn t;}/*** 移除最左边的child* @return*/public Node removeLeftmostChild() {return removeChild(0);}/*** 移除最右边的child* @return*/public Node removeRightmostChild() {return removeChild(keyNumber);}/*** index 孩子处左边的兄弟* @param index* @return*/public Node childLeftSibling(int index) {return index > 0 ? children[index - 1] : null;}/*** index 孩子处右边的兄弟* @param index* @return*/public Node childRightSibling(int index) {return index == keyNumber ? null : children[index + 1];}/*** 复制当前节点的所有key和child到target* @param target*/public void moveToTarget(Node target) {int start = target.keyNumber;if(!leaf) {for (int i = 0; i <= keyNumber; i++) {target.children[start + i] = children[i];}}for (int i = 0; i < keyNumber; i++) {target.keys[target.keyNumber++] = keys[i];}}删除代码:
/*** 删除key* @param key*/public void remove(int key) {doRemove(null, root, 0, key);}private void doRemove(Node parent, Node node, int index, int key) {int i = 0;// 在有效范围内while(i < node.keyNumber) {if(node.keys[i] >= key) {break;}i++;}// 情况1:找到,i代表待删除key的索引// 情况2:没找到,i代表到第i个孩子继续查找if (node.leaf) { // 当前节点是叶子节点if(!found(node,key, i)) { // case 1 没找到return;} else { // case 2 找到了node.removeKey(i);}} else { // 当前节点不是叶子节点if(!found(node,key, i)) { // case 3 没找到// 到孩子节点继续查找doRemove(node, node.children[i], i, key);} else { // case 4 找到了// 1. 找后继keyNode s = node.children[i + 1]; // 当前节点的后一个孩子while(!s.leaf) {// 直到叶子节点,取最左边的s = s.children[0];}int skey = s.keys[0];// 2. 替换待删除keynode.keys[i] = skey;// 3. 删除后继keydoRemove(node, node.children[i + 1], i + 1, skey);}}// 删除后key数目小于下限if(node.keyNumber < MIN_KEY_NUMBER) {// 调整平衡 case 5 case 6balance(parent, node, index);}}/*** 是否找到key* @param node* @param key* @param i* @return*/private boolean found(Node node, int key, int i) {return i < node.keyNumber && node.keys[i] == key;}/*** 调整平衡* @param parent 父节点* @param x 待调整节点* @param i 索引*/private void balance(Node parent, Node x, int i) {// case 6 根节点if(x == root) {if(root.keyNumber == 0 && root.children[0] != null) {root = root.children[0];}return;}// 获取左右两边的兄弟Node left = parent.childLeftSibling(i);Node right = parent.childRightSibling(i);if(left != null && left.keyNumber > MIN_KEY_NUMBER) {// case 5-1 左边富裕,右旋// a) 父节点中前驱key旋转下来x.insertKey(parent.keys[i - 1], 0);if(!left.leaf) {// b) 左边的兄弟不是叶子节点,把最右侧的孩子过继给被调整的节点x.insertChild(left.removeRightmostChild(), 0);}// c) 删除左边兄弟的最右节点,移到父节点(旋转上去)parent.keys[i - 1] = left.removeRightmostKey();return;}if(right != null && right.keyNumber > MIN_KEY_NUMBER) {// case 5-2 右边富裕,左旋// a) 父节点中后去key旋转下来x.insertKey(parent.keys[i], x.keyNumber);if(!right.leaf) {// b) 右边的兄弟不是叶子节点,把最左侧的孩子过继给被调整的节点x.insertChild(right.removeLeftmostChild(), x.keyNumber + 1);}// c) 删除右边兄弟的最左节点,移到父节点(旋转上去)parent.keys[i] = right.removeLeftmostKey();return;}// case 5-3 两边都不富裕,向左合并if(left != null) {// 向左兄弟合并// 将待删除节点从父节点移除parent.removeChild(i);// 从父节点合并一个key到左兄弟left.insertKey(parent.removeKey(i - 1), left.keyNumber);// 将待删除节点的剩余节点和孩子移到到左边x.moveToTarget(left);} else {// 没有左兄弟,向自己合并// 把它的右兄弟移除parent.removeChild(i + 1);// 父节点移除一个key,插入到待删除节点x.insertKey(parent.removeKey(i), x.keyNumber);// 将右兄弟合并过来right.moveToTarget(x);}}8. 完整代码
package com.itheima.datastructure.BTree;import java.util.Arrays;public class BTree {static class Node {int[] keys; // 关键字Node[] children; // 孩子int keyNumber; // 有效关键字数目boolean leaf = true; // 是否是叶子节点int t; // 最小度数public Node(int t) { // t >= 2this.t = t;this.children = new Node[2 * t];this.keys = new int[2 * t - 1];}public Node(int[] keys) {this.keys = keys;}@Overridepublic String toString() {return Arrays.toString(Arrays.copyOfRange(keys, 0, keyNumber));}/*** 多路查找* @param key* @return*/public Node get(int key) {int i = 0;while(i < keyNumber) {if(keys[i] == key) {return this;}if(keys[i] > key) {break;}i++;}// 执行到此时,keys[i] > key 或 i==keyNumberif(leaf) {return null;}// 非叶子节点情况return children[i].get(key);}/*** 向keys指定索引处插入key* @param key* @param index*/public void insertKey(int key, int index) {System.arraycopy(keys, index, keys, index + 1, keyNumber - index);keys[index] = key;keyNumber++;}/*** 向children指定索引处插入child* @param child* @param index*/public void insertChild(Node child, int index) {System.arraycopy(children, index, children, index + 1, keyNumber - index);children[index] = child;}/*** 移除指定index处的key* @param index* @return*/int removeKey(int index) {int t = keys[index];System.arraycopy(keys, index + 1, keys, index, --keyNumber - index);return t;}/*** 移除最左边的key* @return*/public int removeLeftmostKey() {return removeKey(0);}/*** 移除最右边的key* @return*/public int removeRightmostKey() {return removeKey(keyNumber - 1);}/*** 移除指定index处的child* @param index* @return*/public Node removeChild(int index) {Node t = children[index];System.arraycopy(children, index + 1, children, index, keyNumber - index);children[keyNumber] = null; // help GCreturn t;}/*** 移除最左边的child* @return*/public Node removeLeftmostChild() {return removeChild(0);}/*** 移除最右边的child* @return*/public Node removeRightmostChild() {return removeChild(keyNumber);}/*** index 孩子处左边的兄弟* @param index* @return*/public Node childLeftSibling(int index) {return index > 0 ? children[index - 1] : null;}/*** index 孩子处右边的兄弟* @param index* @return*/public Node childRightSibling(int index) {return index == keyNumber ? null : children[index + 1];}/*** 复制当前节点的所有key和child到target* @param target*/public void moveToTarget(Node target) {int start = target.keyNumber;if(!leaf) {for (int i = 0; i <= keyNumber; i++) {target.children[start + i] = children[i];}}for (int i = 0; i < keyNumber; i++) {target.keys[target.keyNumber++] = keys[i];}}}Node root; // 根节点int t; // 树中节点最小度数final int MIN_KEY_NUMBER; // 最小key数目final int MAX_KEY_NUMBER; // 最大key数目public BTree() {this(2);}public BTree(int t) {this.t = t;root = new Node(t);MAX_KEY_NUMBER = 2 * t - 1;MIN_KEY_NUMBER = t - 1;}/*** key是否存在* @param key* @return*/public boolean contains(int key) {return root.get(key) != null;}/*** 新增* @param key*/public void put(int key) {doPut(root, key, null, 0);}private void doPut(Node node, int key, Node parent, int index) {// 1. 查找本节点的插入位置iint i = 0;while(i < node.keyNumber) {if(node.keys[i] == key) {// 更新return;}if(node.keys[i] > key) {break; // 找到插入位置,即为此时的i}i++;}// 2. 如果节点是叶子节点,可以直接插入了if(node.leaf) {node.insertKey(key, i);// 上限}// 3. 如果节点是非叶子节点,需要在children[i]处继续递归插入else {doPut(node.children[i], key, node, i);// 上限}if(isFull(node)) {split(node, parent, index);}}boolean isFull(Node node) {return node.keyNumber == MAX_KEY_NUMBER;}/*** 分裂* @param left 要分裂的节点* @param parent 分裂节点的父节点* @param index 分裂节点是第几个孩子*/private void split(Node left, Node parent, int index) {// 分裂节点为根节点if(parent == null) {Node newRoot = new Node(t);newRoot.leaf = false;newRoot.insertChild(left, 0);this.root = newRoot;parent = newRoot;}// 1. 创建right节点,把left节点中t之后的key和child移动过去Node right = new Node(t);// 新增节点是否是叶子节点与待分裂节点一致right.leaf = left.leaf;System.arraycopy(left.keys, t, right.keys, 0, t - 1);// 如果分裂节点为非叶子节点if(!left.leaf) {System.arraycopy(left.children, t, right.children, 0, t);}right.keyNumber = t - 1;left.keyNumber = t - 1;// 2. 中间的key(t - 1处)插入到父节点int mid = left.keys[t - 1];parent.insertKey(mid, index);// 3. right节点作为父节点的孩子parent.insertChild(right, index + 1);}/*** 删除key* @param key*/public void remove(int key) {doRemove(null, root, 0, key);}private void doRemove(Node parent, Node node, int index, int key) {int i = 0;// 在有效范围内while(i < node.keyNumber) {if(node.keys[i] >= key) {break;}i++;}// 情况1:找到,i代表待删除key的索引// 情况2:没找到,i代表到第i个孩子继续查找if (node.leaf) { // 当前节点是叶子节点if(!found(node,key, i)) { // case 1 没找到return;} else { // case 2 找到了node.removeKey(i);}} else { // 当前节点不是叶子节点if(!found(node,key, i)) { // case 3 没找到// 到孩子节点继续查找doRemove(node, node.children[i], i, key);} else { // case 4 找到了// 1. 找后继keyNode s = node.children[i + 1]; // 当前节点的后一个孩子while(!s.leaf) {// 直到叶子节点,取最左边的s = s.children[0];}int skey = s.keys[0];// 2. 替换待删除keynode.keys[i] = skey;// 3. 删除后继keydoRemove(node, node.children[i + 1], i + 1, skey);}}// 删除后key数目小于下限if(node.keyNumber < MIN_KEY_NUMBER) {// 调整平衡 case 5 case 6balance(parent, node, index);}}/*** 是否找到key* @param node* @param key* @param i* @return*/private boolean found(Node node, int key, int i) {return i < node.keyNumber && node.keys[i] == key;}/*** 调整平衡* @param parent 父节点* @param x 待调整节点* @param i 索引*/private void balance(Node parent, Node x, int i) {// case 6 根节点不平衡if(x == root) {if(root.keyNumber == 0 && root.children[0] != null) {root = root.children[0];}return;}// 获取左右两边的兄弟Node left = parent.childLeftSibling(i);Node right = parent.childRightSibling(i);if(left != null && left.keyNumber > MIN_KEY_NUMBER) {// case 5-1 左边富裕,右旋// a) 父节点中前驱key旋转下来x.insertKey(parent.keys[i - 1], 0);if(!left.leaf) {// b) 左边的兄弟不是叶子节点,把最右侧的孩子过继给被调整的节点x.insertChild(left.removeRightmostChild(), 0);}// c) 删除左边兄弟的最右节点,移到父节点(旋转上去)parent.keys[i - 1] = left.removeRightmostKey();return;}if(right != null && right.keyNumber > MIN_KEY_NUMBER) {// case 5-2 右边富裕,左旋// a) 父节点中后去key旋转下来x.insertKey(parent.keys[i], x.keyNumber);if(!right.leaf) {// b) 右边的兄弟不是叶子节点,把最左侧的孩子过继给被调整的节点x.insertChild(right.removeLeftmostChild(), x.keyNumber + 1);}// c) 删除右边兄弟的最左节点,移到父节点(旋转上去)parent.keys[i] = right.removeLeftmostKey();return;}// case 5-3 两边都不富裕,向左合并if(left != null) {// 向左兄弟合并// 将待删除节点从父节点移除parent.removeChild(i);// 从父节点合并一个key到左兄弟left.insertKey(parent.removeKey(i - 1), left.keyNumber);// 将待删除节点的剩余节点和孩子移到到左边x.moveToTarget(left);} else {// 没有左兄弟,向自己合并// 把它的右兄弟移除parent.removeChild(i + 1);// 父节点移除一个key,插入到待删除节点x.insertKey(parent.removeKey(i), x.keyNumber);// 将右兄弟合并过来right.moveToTarget(x);}}}
B站视频链接:基础算法-175-B树-remove-演示2_哔哩哔哩_bilibili
相关文章:

数据结构与算法 - B树
一、概述 1. 历史 B树(B-Tree)结构是一种高效存储和查询数据的方法,它的历史可以追溯到1970年代早期。B树的发明人Rudolf Bayer和Edward M. McCreight分别发表了一篇论文介绍了B树。这篇论文是1972年发表于《ACM Transactions on Database Systems》中的ÿ…...

Java二十三种设计模式-观察者模式(15/23)
观察者模式:实现对象间的松耦合通知机制 引言 在当今的软件开发领域,设计模式已成为创建可维护、可扩展和可重用代码的基石。在众多设计模式中,观察者模式以其独特的能力,实现对象间的松耦合通信而脱颖而出。本文将深入探讨观察…...

opencv-python图像增强二:图像去雾(暗通道去雾)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、简介:二、暗通道去雾方案简述:三、算法实现步骤3.1最小值滤波3.2 引导滤波3.3 计算图像全局光强 四:整体代码实现五…...

自研Vue3低代码海报制作平台第一步:基础拖拽组件开发
学习来源:稀土掘金 - 幽月之格大佬的技术专栏可拖拽、缩放、旋转组件 - 著作:可拖拽、缩放、旋转组件实现细节 非常感谢大佬!受益匪浅! 前面我们学习了很多vue3的知识,是时候把它们用起来做一个有意思的平台…...

QT 的 QSettings 读写 INI 文件的示例
在Qt中,QSettings 类提供了一种便捷的方式来存储和访问应用程序的设置,这些设置可以存储在多种格式的文件中,包括INI、Windows注册表(仅Windows平台)、XML和JSON等。以下是一些使用 QSettings 读写INI文件的示例。 写…...

【零基础学习CAPL语法】——testStep:测试结果输出函数
文章目录 1.函数介绍2.在报告中体现 1.函数介绍 testStep——测试结果输出函数 2.在报告中体现 //testStep() void PrintTxMsg() {testStep("Tx","[%x] [%.2x %.2x %.2x %.2x %.2x %.2x %.2x %.2x]",Diag_Req.id,Diag_Req.byte(0),Diag_Req.byte(1),Di…...

8.5.数据库基础技术-规范化
函数依赖 函数依赖:给定一个X,能唯一确定一个Y,就称X决定(确定)Y,或者说Y依赖于X。 例如:YX*X函数,此时X能确定Y的值,但是Y无法确定X的值,比如x2,y4,但是y4无法确定x2。函数依赖又可扩展以下两…...

于博士Cadence视频教程学习笔记备忘
标签:PCB教程 PCB设计步骤 cadence教程 Allegro教程 以下是我学习该视频教程的笔记,记录下备忘,欢迎大家在此基础上完善,能回传我一份是最好了,先谢过。 备注: 1、未掌握即未进行操作 2、操作软件是15.…...

8.3.数据库基础技术-关系代数
并:结果是两张表中所有记录数合并,相同记录只显示一次。交:结果是两张表中相同的记录。差:S1-S2,结果是S1表中有而S2表中没有的那些记录。 笛卡尔积:S1XS2,产生的结果包括S1和S2的所有属性列,并且S1中每条记…...
【Vue3】vue模板中如何使用enum枚举类型
简言 有的时候,我们想在vue模板中直接使用枚举类型的值,来做一些判断。 ts枚举 枚举允许开发人员定义一组命名常量。使用枚举可以更容易地记录意图,或创建一组不同的情况。TypeScript 提供了基于数字和字符串的枚举。 枚举的定义这里不说了…...

组合求和2
题目描述: Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sum to target. Each number in candidates may only be used once in the combinati…...
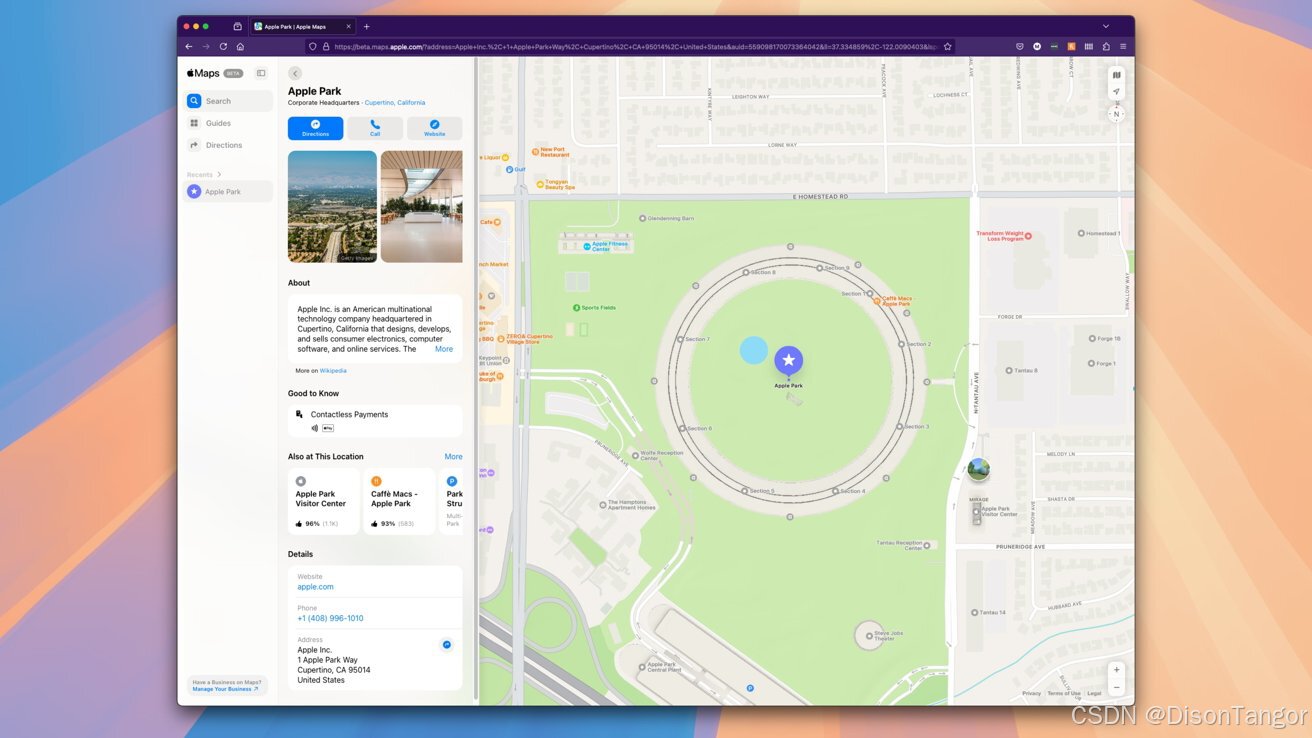
Apple Maps现在可在Firefox和Mac版Edge浏览器中使用
Apple Maps最初只能在 Windows 版 Safari、Chrome 浏览器和 Edge 浏览器上运行,现在已在其他浏览器上运行,包括 Mac 版 Firefox 和 Edge。经过十多年的等待,Apple Maps于今年 7 月推出了新版地图应用的测试版,但只能在有限的浏览器…...
基于嵌入式Linux的数据库
数据库 数据库是在数据库管理系统和控制之下,存放在存储 介质上的数据集合。 基于嵌入式的数据库 基于嵌入式linux的数据库主要有SQlite, Firebird,Berkeley DB,eXtremeDB Firebird是关系型数据库,功能强大,支持存储过 程&…...

C# 使用LINQ找出一个子字符串在另一个字符串中出现的所有位置
一、实现步骤 遍历主字符串,使用IndexOf方法查找子字符串的位置。如果找到了子字符串,记录其位置,并且从该位置的后面继续查找。重复上述步骤直到遍历完整个字符串。 二、简单代码示例 using System; using System.Collections.Generic; usi…...
)
YOLOv8添加MobileViTv3模块(代码+free)
目录 一、理由 二、方法 (1)导入MobileViTv3模块 (2)在ultralytics/nn/tasks.py的函数parse_model中修改 (3)在yaml配置文件中写入 (4)开始训练,先把其他梯度关闭&…...

从概念到落地:全面解析DApp项目开发的核心要素与未来趋势
随着区块链技术的迅猛发展,去中心化应用程序(DApp)逐渐成为Web3时代的重要组成部分。DApp通过智能合约和分布式账本技术,提供了无需信任中介的解决方案,这种去中心化的特性使其在金融、游戏、社交等多个领域得到了广泛…...
仓颉编程入门 -- 泛型概述 , 如何定义泛型函数
泛型概述 , 如何定义泛型函数 1 . 泛型的定义 在仓颉编程语言中,泛型机制允许我们定义参数化类型,这些类型在声明时不具体指定其操作的数据类型,而是作为类型形参保留,待使用时通过类型实参来明确。这种灵活性在函数和类型声明中…...

SOC估算方法之(OCV-SOC+安时积分法)
一、引言 此方法主要参考电动汽车用磷酸铁锂电池SOC估算方法这篇论文 总结: 开路电压的测量需要将电池静止相当长的一段时间才能达到平衡状态进行测量。 安时积分法存在初始SOC的估算和累积的误差。 所以上述两种方法都存在一定的缺陷,因此下面主要讲…...
)
指针(下)
文章目录 指针(下)野指针、空指针野指针空指针 二级指针**main**函数的原型说明 常量指针与指针常量常量指针指针常量常量指针常量 动态内存分配常用函数**malloc****calloc****realloc****free** **void**与**void***的区别扩展:形式参数和实际参数的对应关系 指针…...

C# 浅谈IEnumerable
一、IEnumerable 简介 IEnumerable 是一个接口,它定义了对集合进行迭代所需的方法。IEnumerable 接口主要用于允许开发者使用foreach循环来遍历集合中的元素。这个接口定义了一个名为 GetEnumerator 的方法,该方法返回一个实现了 IEnumerator 接口的对象…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
