【经典算法】BFS_最短路问题
目录
- 1. 最短路问题介绍
- 2. 算法原理和代码实现(含题目链接)
- 1926.迷宫中离入口最近的出口
- 433.最小基因变化
- 127.单词接龙
- 675.为高尔夫比赛砍树
- 3. 算法总结
1. 最短路问题介绍
最短路径问题是图论中的一类十分重要的问题。本篇文章只介绍边权为1(或边权相同)的最简单的最短路径问题。所谓边权,就是两点之间的距离。
这类问题通俗的说就是告诉你起点和终点,要你找出最短的路径或是最短路径是多少。
解决方法:从起点开始,来一次bfs即可。
A出队列后,向外扩展一层,B,C入队列,注意,此时出队列要B,C同时出(其实是写一个for循环,先B后C)。
那如何计算出最短路径是多少呢?
扩展的层数,就是最短路的长度。
2. 算法原理和代码实现(含题目链接)
1926.迷宫中离入口最近的出口



算法原理:
我们可以从起点开始层序遍历,并且在遍历的过程中记录当前遍历的层数。这样就能在找到出⼝的时候,得到起点到出⼝的最短距离。
把题目抽象为:从当前位置出发,到离边界上的那个点的最短路程是多少。
细节/技巧问题:
(1) 人当前所在位置不能当做出口。
(2) 出口:与边界相邻的空格就是出口。
(3) 人在移动时仅需走到出口位置即可,不需要走出迷宫。
代码实现:
class Solution
{int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};public:int nearestExit(vector<vector<char>>& maze, vector<int>& e) {int m = maze.size(), n = maze[0].size();bool vis[m][n];memset(vis, 0, sizeof(vis));queue<pair<int, int>> q;q.push({e[0], e[1]});vis[e[0]][e[1]] = true;int step = 0; // 记录步数while(q.size()){step++;int sz = q.size();// 假设进去sz个,要同时出for(int i = 0; i < sz; i++){auto[a,b] = q.front();q.pop();for(int j = 0; j < 4; j++){int x = a+dx[j], y = b+dy[j];if(x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == '.' && !vis[x][y]){// 判断是否到达出口了if(x == 0 || x == m-1 || y == 0 || y == n-1)return step;else{q.push({x, y});vis[x][y] = true;}}}}}return -1;}
};
433.最小基因变化


算法原理:
如果将每次字符串的变换抽象成图中的两个点和⼀条边的话,问题就变成了边权为1的最短路题。
其他细节/技巧问题:
(1) 原字符串每个字符变化后一定存在相同的,此时要用哈希表来标记搜索的状态,每次变化后都扔进哈希表中。
(2) 如何枚举出所有的变化情况呢?直接两层for循环。
(3) 变化成哪种字符串才能入队列呢?变化后的字符串在基因库中存在时,才队列。所以把基因库里的字符串扔进哈希表中,每次变化后都要判断是否在基因库中。
代码实现:
class Solution
{
public:int minMutation(string startGene, string endGene, vector<string>& bank) {unordered_set<string> vis; // 记录字符串是否搜索过 unordered_set<string> hash(bank.begin(), bank.end()); // 判断变化后的字符串是否在库中//处理特殊情况if(startGene == endGene) return 0;if(!hash.count(endGene)) return -1;queue<string> q;q.push(startGene);vis.insert(startGene);string change = "AGCT";int ret = 0; //记录变化次数while(q.size()){ret++; // 就是往外扩展了一层int sz = q.size();// 每次都要同时出队列while(sz--){string t = q.front();q.pop();// 变化过程for(int i = 0; i < 8; i++){string tmp = t; //每次只变化一个字符for(int j = 0; j < 4; j++){tmp[i] = change[j];// 在基因库中并且没有被搜索过if(hash.count(tmp) && !vis.count(tmp)){// 判断是否已经结束if(tmp == endGene) return ret;q.push(tmp);vis.insert(tmp);}}}}}return -1;}
};
127.单词接龙


算法原理:
这道题和第二题基本一模一样,都是把一个字符串变化成目标字符串,唯一不同的是本题统计的是整个过程中单词的个数,其实就是上一题的最小次数+1。
细节/技巧问题:
参考前两题
代码实现:
class Solution
{
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {unordered_set<string> hash(wordList.begin(), wordList.end());unordered_set<string> vis; // 标记已经搜索过的//if(beginWord == endWord) return 1;if(!hash.count(endWord)) return 0;queue<string> q;q.push(beginWord);vis.insert(beginWord);int ret = 0;while(q.size()){ret++;int sz = q.size();while(sz--){string t = q.front();q.pop();for(int i = 0; i < 10; i++){string tmp = t;for(char ch = 'a'; ch <= 'z'; ch++){tmp[i] = ch; // 每次只修改一个字符// 存在列表中并且没有被访问过if(!vis.count(tmp) && hash.count(tmp)){if(tmp == endWord) return ret+1; q.push(tmp);vis.insert(tmp);}}}}}return 0;}
};
675.为高尔夫比赛砍树


算法原理:
这道题目确实很难。
这道题可以抽象成若干个迷宫问题。我们只要计算出从这一棵树到下一棵树的最少步数,再把所有的步数相加,就可以求出砍完所有树的最少步数。所以这里要多次使用bfs算法,写成函数,它的作用是统计两棵树之间的最少步数。
难点/细节/技巧问题:
(1) 树的坐标如何存储。使用vector容器。
(2) 由于要按照高度从低到高开始砍,所以先要把树的高度排升序。
(3) bfs的参数是传起点和终点。
代码实现:
class Solution
{int m, n;int dx[4] = {0,0,1,-1};int dy[4] = {1,-1,0,0};public:int cutOffTree(vector<vector<int>>& f) {m = f.size(), n = f[0].size();// 记录树的位置vector<pair<int, int>> trees;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(f[i][j] > 1) trees.push_back({i, j}); // 是树,才记录坐标// 从低到高开始砍sort(trees.begin(), trees.end(), [&](const pair<int, int>& p1,const pair<int, int>& p2){return f[p1.first][p1.second] < f[p2.first][p2.second];});int bx = 0, by = 0; // 起始位置int step = 0;for(auto& [a,b] : trees){// 使用bfs计算两树之间的最短路int ret = bfs(f, bx, by, a, b);if(ret == -1) return -1;step += ret;bx = a, by = b; // 更新下一个位置的坐标}return step;}bool vis[51][51];int bfs(vector<vector<int>>& f, int bx, int by, int ex, int ey){if(bx == ex && by == ey) return 0;memset(vis, 0, sizeof(vis)); // 每次计算都要把标记还原queue<pair<int ,int>> q;q.push({bx, by});vis[bx][by] = true;int ret = 0; // 记录每两颗树之间的最短步数while(q.size()){ret++;int sz = q.size();while(sz--){auto[a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = a+dx[k], y = b+dy[k];if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && f[x][y]){// 判断是否走到终点if(x == ex && y == ey) return ret;q.push({x, y});vis[x][y] = true;}}}}return -1;}
};
3. 算法总结
bfs算法是解决最短路问题的经典方法。我感觉解决最短路问题核心的关键是每一次出队列时都要把上一次入队列的数据全部出完(就要写for循环),而最短路程就是向外扩展的层数。
相关文章:

【经典算法】BFS_最短路问题
目录 1. 最短路问题介绍2. 算法原理和代码实现(含题目链接)1926.迷宫中离入口最近的出口433.最小基因变化127.单词接龙675.为高尔夫比赛砍树 3. 算法总结 1. 最短路问题介绍 最短路径问题是图论中的一类十分重要的问题。本篇文章只介绍边权为1(或边权相同)的最简单的最短路径问…...

【题目/训练】:双指针
引言 我们已经在这篇博客【算法/学习】双指针-CSDN博客里面讲了双指针、二分等的相关知识。 现在我们来做一些训练吧 经典例题 1. 移动零 思路: 使用 0 当做这个中间点,把不等于 0(注意题目没说不能有负数)的放到中间点的左边,等于 0 的…...

LLVM - 编译器后端-指令选择
一:概述 任何后端的核心都是指令选择。LLVM 实现了几种方法;在本篇文章中,我们将通过选择有向无环图(DAG)和全局指令选择来实现指令选择。 在本篇文章中,我们将学习以下主题: • 定义调…...
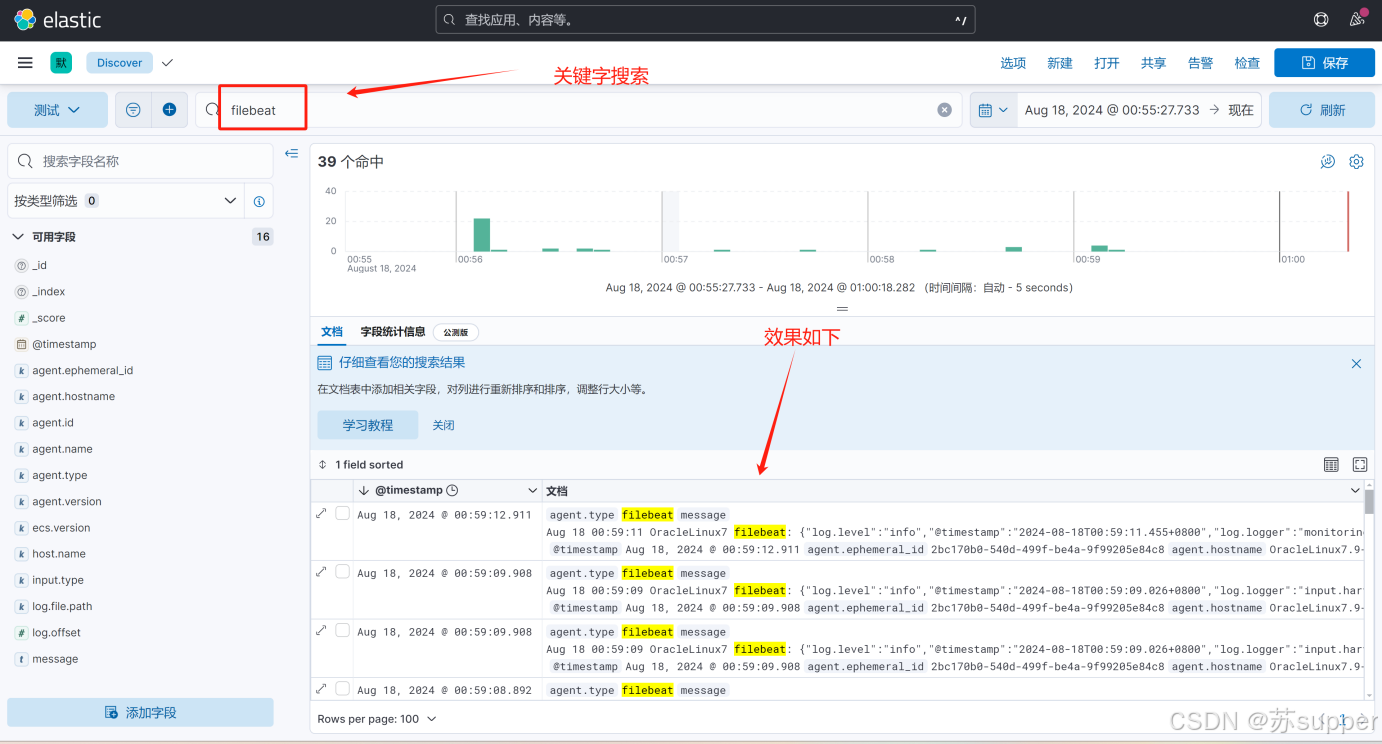
ES+FileBeat+Kibana日志采集搭建体验
1.环境准备 需要linux操作系统,并安装了docker环境 此处使用虚拟机演示。(虚拟机和docker看参考我之前写的文章) VirtualBox安装Oracle Linux 7.9全流程-CSDN博客 VirtualBox上的Oracle Linux虚拟机安装Docker全流程-CSDN博客 简单演示搭建ES…...

Dockerfile常用指令详解
Dockerfile 是一个用于定义 Docker 镜像构建过程的脚本文件,其中包含了一系列指令,用于指定如何构建和配置镜像。以下是一些常用的 Dockerfile 指令及其示例用法: 1. FROM 指定基础镜像,Dockerfile 必须以该指令开始。 示例&am…...

【vue】浏览器兼容相关
Vue.js 是一个流行的前端 JavaScript 框架,它支持构建单页应用和复杂的用户界面。Vue.js 的核心库本身对浏览器的支持情况如下: Vue.js 2.x 最低支持版本:IE9 及以上版本。特性支持:ES5。兼容性:Vue 2.x 在发布时就考…...

【区块链+金融服务】基于区块链的区域股权金融综合服务平台 | FISCO BCOS应用案例
区域性股权市场是我国资本市场的重要组成部分,是多层次资本市场体系的基石。区块链技术与区域性股权市场 分散特征天然匹配,从新型金融基础设施层面为场外参与各方提供公共的可信服务,以技术手段完善市场基础条 件,弥补区域性短板…...

string字符串和json对象相互转换问题
//响应体String responseStr EntityUtils.toString(response.getEntity());log.debug("下单响应码:{},响应体:{}",statusCode,responseStr);if(statusCode HttpStatus.OK.value()){JSONObject jsonObject JSONObject.parseObject(responseStr);if(jsonObject.cont…...

【生成式人工智能-十一一个不修改模型就能加速语言模型生成的方法】
一个加速语言模型生成的方法 现在语言模型的一个弊端speculative decoding预言家预测的问题 speculative decoding 模块的实现方法NAT Non-autoregressive模型压缩使用搜索引擎 一些更复杂些的speculative decoding 实现方式 speculative decoding 是一个适用于目前生成模型的加…...

Rust 错误处理
Rust 错误处理 Rust 是一种系统编程语言,以其内存安全、高并发和实用性而著称。在 Rust 中,错误处理是一个核心概念,它通过提供 Result 和 Option 类型来鼓励开发者显式地处理可能出现的错误,而不是依赖异常机制。本文将深入探讨 Rust 中的错误处理机制,包括 Result 和 O…...

程序与进程 linux系统
程序与进程 程序 ( program ): 通常为 binary program ,放置在储存媒体中(如硬盘、光盘、软盘、磁带等), 为实体文件的型态存在;二进制文件,比如静态 /bin/date…...

使用MongoDB构建AI:Story Tools Studio将生成式AI引入Myth Maker AI游戏
Story Tools Studio利用先进的生成式AI技术,打造沉浸式、个性化、无穷尽的情景体验。 Story Tools Studio创始人兼首席执行官Roy Altman表示:“我们的旗舰游戏Myth Maker AI采用的是我们自主研发的、以AI为驱动的专家指导型故事生成器MUSE,它…...
)
鸿蒙UIAbility组件概述(二)
鸿蒙UIAbility组件概述 UIAbility组件基本用法指定UIAbility的启动页面获取UIAbility的上下文信息 UIAbility组件与UI的数据同步使用EventHub进行数据通信使用AppStorage/LocalStorage进行数据同步 UIAbility组件间交互(设备内)启动应用内的UIAbility启动…...
如何优化SQL查询?)
Oracle(70)如何优化SQL查询?
优化SQL查询是数据库管理的重要部分,旨在提高查询性能,减少响应时间和资源消耗。以下是一些常见的SQL查询优化技术,结合代码示例详细说明。 1. 使用索引 索引是优化查询性能的最常见方法之一。索引可以显著减少数据检索的时间。 示例 假设…...

深度剖析:Jenkins构建任务无法中断的原因及解决方案
个人名片 🎓作者简介:java领域优质创作者 🌐个人主页:码农阿豪 📞工作室:新空间代码工作室(提供各种软件服务) 💌个人邮箱:[2435024119qq.com] 📱…...

【YOLO】常用脚本
目录 VOC转YOLO划分训练集、测试集与验证集 VOC转YOLO import os import xml.etree.ElementTree as ETdef convert(size, box):dw 1. / size[0]dh 1. / size[1]x (box[0] box[1]) / 2.0y (box[2] box[3]) / 2.0w box[1] - box[0]h box[3] - box[2]x x * dww w * dwy…...

Springboot IOC DI理解及实现+JUnit的引入+参数配置
一、JavaConfig 我们通常使用 Spring 都会使用 XML 配置,随着功能以及业务逻辑的日益复杂,应用伴随着大量的 XML 配置文件以及复杂的 bean 依赖关系,使用起来很不方便。 在 Spring 3.0 开始,Spring 官方就已经开始推荐使用 Java…...

CeresPCL 最小二乘插值(曲线拟合)
一、简介 在多项式插值时,当数据点个数较多时,插值会导致多项式曲线阶数过高,带来不稳定因素。因此我们可以通过固定幂基函数的最高次数 m(m < n),来对我们要拟合的曲线进行降阶。之前的函数形式就可以变为: 既然是最小二乘问题,那么就仍然可以使用Ceres来进行求解。 …...

【TCP/IP】自定义应用层协议,常见端口号
互联网中,主流的是 TCP/IP 五层协议 5G/4G 上网,是有自己的协议栈,要比 TCP/IP 更复杂(能够把 TCP/IP 的一部分内容给包含进去了) 应用层 可以代表我们所编写的应用程序,只要应用程序里面用到了网络通信…...

Frida 的下载和安装
首先要安装好 python 环境 安装 frida 和 工具包 pip install frida frida-tools 查看版本: frida --version 16.4.8 然后到 github 上下载对应 server ( 和frida 的版本一致 16.4.8) Releases frida/frida (github.com) 查看手机或…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...



