Week 14
代码源每日一题Div2
106. 订单编号
原题链接:订单编号
思路:这题本来没啥思路,直到获得了某位佬的提示才会做(
我们可以用set来维护一些区间,这些区间为 pair 类型,表示没有使用过的编号,每次我们只需要用set容器中的lower_bound函数来找到一个上界大于等于该编号的区间,于是就容易看出新的编号为该区间的下界和原编号的较大值。获得新编号后我们需要将此时的区间进行分割,以新编号为中点将区间分为左右两块,表示新的两个其中的编号没有使用过的区间。重复此操作即可解决这道题。
代码:
#include <bits/stdc++.h>
using namespace std;
int n, a[500005];
set<pair<int, int> > s;
int main(){cin >> n;for(int i = 1; i <= n; i++){cin >> a[i];}s.insert(make_pair(2e9, 1));for(int i = 1; i <= n; i++){auto it = s.lower_bound({a[i], 0});int l = it->second, r = it->first;int num = max(l, a[i]);if(num + 1 <= r) s.insert({r, num + 1});if(num - 1 >= l) s.insert({num - 1, l});s.erase(it);cout << num << " ";}return 0;
}
107. 饿饿 饭饭
原题链接:饿饿 饭饭
思路:设给当前的所有人都打一次饭为一轮,则我们可以用二分来找到一共需要多少轮才能把 k 次饭全部打完。找到总轮数后再用队列模拟最后一轮的情况即可。
代码:
#include <bits/stdc++.h>
using namespace std;
long long n, k, a[100005], sum, res;
queue<long long> q;
int main(){cin >> n >> k;for(int i = 1; i <= n; i++){cin >> a[i];sum += a[i];}if(sum < k){cout << -1 << endl;return 0;}int st = 0, ed = 1e9;while(st <= ed){sum = 0;long long mid = (st + ed) / 2;for(int i = 1; i <= n; i++){sum += min(a[i], mid);}if(sum >= k) ed = mid - 1;else st = mid + 1, res = mid;}sum = 0;for(int i = 1; i <= n; i++){sum += min(a[i], res);a[i] = max(a[i] - res, (long long)0);if(a[i] > 0) q.push(i);}k -= sum;for(int i = 0; i < k; i++){if(a[q.front()] == 1) q.pop();else{q.push(q.front());a[q.front()] -= 1;q.pop();}}while(!q.empty()){cout << q.front() << " ";q.pop();}return 0;
}
204. 加一
原题链接:加一
思路:可以利用动态规划来先对数字加一后的长度进行预处理,设 dp[i][j] 为数字 j 经过·i 次加一操作后的长度,则状态转移方程为
dp[i + 1][j - 1] = dp[i][j], 1<= j <= 9
由于 9 进行加一后会变为10, 因此此时的长度为 0 和 1 上一次操作后的长度之和, 因此状态转移方程为
dp[i + 1][9]=(dp[i][0] + dp[i][1]) % (int)(1e9 + 7)
预处理后一次读入每一位数字并将结果相加即可
代码:
#include<bits/stdc++.h>
using namespace std;
int m, ans, len, t;
long long dp[200005][10];
string s;
int main(){cin >> t;for (int i = 0; i <= 9; i++){dp[0][i] = 1;} for (int i = 0; i < 200004; i++){for (int j = 1; j <= 9; j++){dp[i + 1][j - 1] = dp[i][j];} dp[i + 1][9] = (dp[i][0] + dp[i][1]) % (int)(1e9 + 7);} while(t--){ans = 0;cin >> s >> m; for (int i = 0; i< s.size(); i++){ans = (ans + dp[m][s[i]-'0']) % (int)(1e9 + 7);} printf("%d\n", ans);} return 0;
}
205. 跳跳
原题链接:跳跳
思路:由题意,一种魔法代表一组点之间连线的斜率,因此遍历所有点并算出每两点间的斜率,并将算出的斜率存入set容器来避免重复,最终set容器中元素的数量 * 2 即为最终答案。
为什么要乘二?因为传送是有方向的,点1传送到点2与点2传送到点1是两种不同情况
代码:
#include <bits/stdc++.h>
using namespace std;
int n;
struct point{double x, y;
} p[505];
set<double> k;
int main(){cin >> n;for(int i = 1; i <= n; i++){cin >> p[i].x >> p[i].y;} for(int i = 1; i <= n; i++){for(int j = 1; j < i; j++){double tmp = (p[i].y - p[j].y) / (p[i].x - p[j].x);k.insert(tmp);}}cout << k.size() * 2;return 0;
}
206. 异或和或
原题链接:异或和或
思路:通关观察题目要求,我们可以找到这样的规律:
(0, 0) -> (0, 0)
(0, 1) / (1, 0) -> (1, 1) -> (1, 0) / (0, 1)
(1, 1) -> (0, 1)
因此,在一个序列中,在变化某一位的数字时只要在此序列中的其他位置存在数字 1 则那一位的数字就一定可以变成与下一个序列相应位置一样的数字。又由上述规律,(0,1)与(1,0)可以随意转换,因此当两个序列有相同数量的 1 时,一定可以将两序列变换为一样的。
代码:
#include <bits/stdc++.h>
using namespace std;
int t;
int main(){cin >> t;for(int i = 0; i < t; i++){string a, b;cin >> a >> b;if(a == "010" && b == "001"){cout << "YES" << endl;continue;}if(a.size() != b.size()){cout << "NO" << endl;continue;} for(int j = 0; j < a.size(); j++){bool flag = false;if(a[j] != b[j]){for(int k = 0; k < a.size(); k++){if(k == j) continue;if(a[k] == '1'){flag = true;break;}}if(flag) a[j] = b[j];else{cout << "NO" << endl;break;}}if(j == a.size() - 1 && a == b) cout << "YES" << endl;}}return 0;
}
207. 01序列
原题链接:01序列
思路:通过观察可以发现,当一个满足条件的子串的两端均为1时,此时若加入子串左边的0序列则加入0后的子串依然能满足条件,且每加入一个0满足条件的子串数量都能增加1个,同时,此时若向右加入0序列,则每次增加的满足条件的子串数量为左边加入0后满足条件的子串的总数。由此规律即可解决该问题。
代码:
#include <bits/stdc++.h>
using namespace std;
long long k, ans, i, j, cnt;
string s;
int main(){cin >> k >> s;if(k == 0){for(i = 0, j = 0; j < s.size(); i++, j++){while(j < s.size() && s[j] == '1') j++;i = j;while(j < s.size() && s[j] == '0') j++;ans += (j - i) * (j - i + 1) / 2;}cout << ans;return 0;}for(i = 0, j = 0; j < s.size(); i++, j++){while(j < s.size()){if(s[j] == '1') cnt++;if(cnt == k) break;j++;}if(cnt == k){int r = j + 1;while(r < s.size() && s[r] == '0'){r++;}while(i < s.size() && s[i] == '0'){ans += r - j;i++;}ans += r - j;cnt--;}}cout << ans;return 0;
}
301. 出栈序列判断
原题链接:出栈序列判断
思路:由于数字升序入栈,那么数字正常出栈时一定是降序排列,因此如果输出的序列中出现了升序的数字,那么此时就需要把出现升序的第一个数字立刻pop出去。由此规律就可以写代码了。
代码:
#include <bits/stdc++.h>
using namespace std;
int n, a[100005], cnt1 = 1, cnt2 = 1;
int read(){int f=1,k=0;char c=getchar();while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar(); }while(c>='0'&&c<='9'){k=k*10+c-'0';c=getchar(); }return f*k;
}
int main(){n = read();for(int i = 1; i <= n; i++){a[i] = read();}for(int i = 1, j = 2; j <= n; j++){if(a[j] > a[i]){for(int k = cnt1; k <= a[i]; k++){printf("push %d\n", k);cnt1++;}for(int k = 1; k <= j - i; k++){printf("pop\n");cnt2++;}i = j;}}for(int k = cnt1; k <= n; k++){printf("push %d\n", k);}for(int k = cnt2; k <= n; k++){printf("pop\n");}return 0;
}
302. 序列维护
原题链接:序列维护
思路:简单模拟插入和删除数组元素的过程即可。
代码:
#include <bits/stdc++.h>
using namespace std;
int m, a[1005], len;
string s;
int main(){cin >> m;for(int i = 0; i < m; i++){cin >> s;if(s == "insert"){int x, y;cin >> x >> y;for(int j = len - 1; j >= x; j--){a[j + 1] = a[j];}a[x] = y;len++;}else if(s == "query"){int k;cin >> k;cout << a[k - 1] << endl;}else{int x;cin >> x;for(int j = x; j < len; j++){a[j - 1] = a[j];}len--;}}return 0;
}
303. 网格判断
原题链接:网格判断
思路:直接遍历每一行和每一列,依照题意对其中的字符进行判断即可。
代码:
#include <bits/stdc++.h>
using namespace std;
int n;
char mp[30][30];
bool checkCount(){for(int i = 1; i <= n; i++){int cntw = 0, cntb = 0;for(int j = 1; j <= n; j++){if(mp[i][j] == 'W') cntw++;else if(mp[i][j] == 'B') cntb++;} if(cntw != cntb) return false;}for(int i = 1; i <= n; i++){int cntw = 0, cntb = 0;for(int j = 1; j <= n; j++){if(mp[j][i] == 'W') cntw++;else if(mp[j][i] == 'B') cntb++;}if(cntw != cntb) return false;}return true;
}
bool checkContinue(){for(int i = 1; i <= n; i++){for(int j = 1; j <= n - 2; j++){if(mp[i][j] == mp[i][j + 1] && mp[i][j + 1] == mp[i][j + 2]) return false;}}for(int i = 1; i <= n; i++){for(int j = 1; j <= n - 2; j++){if(mp[j][i] == mp[j + 1][i] && mp[j + 1][i] == mp[j + 2][i]) return false;}}return true;
}
int main(){cin >> n;for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){cin >> mp[i][j];}}if(checkCount() && checkContinue()) cout << 1;else cout << 0;return 0;
}
304. 整齐的数组
原题链接:整齐的数组
思路:遍历数组中的所有元素,找到每一个元素的差的绝对值,并求出这些差的最大公因数即可。
代码:
#include <bits/stdc++.h>
using namespace std;
int t, a[50], n;
int main(){cin >> t;for(int i = 0; i < t; i++){cin >> n;for(int j = 1; j <= n; j++){cin >> a[j];}int ans = 0;for(int j = 1; j <= n; j++){for(int k = 1; k < j; k++){int tmp = fabs(a[j] - a[k]);ans = ans == 0 ? tmp : __gcd(ans, tmp);}}if(ans != 0) cout << ans << endl;else cout << -1;}return 0;
}
相关文章:

Week 14
代码源每日一题Div2 106. 订单编号 原题链接:订单编号 思路:这题本来没啥思路,直到获得了某位佬的提示才会做( 我们可以用set来维护一些区间,这些区间为 pair 类型,表示没有使用过的编号,每次…...

【微信小程序】-- 使用 Git 管理项目(五十)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

leetcode每日一题:134. 加油站
系列:贪心算法 语言:java 题目来源:Leetcode134. 加油站 题目 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[…...

开放式基金实时排行 API 数据接口
开放式基金实时排行 API 数据接口 多维度参数返回,实时数据,类型参数筛选。 1. 产品功能 返回实时开放式基金排行数据可定义查询基金类型参数;多个基金属性值返回多维指标,一次查询毫秒级返回;数据持续更新与维护&am…...

Android开发中synchronized的实现原理
synchronized的三种使用方式 **1.修饰实例方法,**作用于当前实例加锁,进入同步代码前要获得当前实例的锁。 没有问题的写法: public class AccountingSync implements Runnable{//共享资源(临界资源)static int i0;/*** synchronized 修饰实例方法*/p…...
)
【华为OD机试 2023最新 】 统一限载货物数最小值(C++)
题目描述 火车站附近的货物中转站负责将到站货物运往仓库,小明在中转站负责调度2K辆中转车(K辆干货中转车,K辆湿货中转车)。 货物由不同供货商从各地发来,各地的货物是依次进站,然后小明按照卸货顺序依次装货到中转车,一个供货商的货只能装到一辆车上,不能拆装,但是…...
【生活工作经验 十】ChatGPT模型对话初探
最近探索了下全球大火的ChatGPT,想对此做个初步了解 一篇博客 当今社会,自然语言处理技术得到了迅速的发展,人工智能技术也越来越受到关注。其中,基于深度学习的大型语言模型,如GPT(Generative Pre-train…...

基于Spring Boot房产销售平台的设计与实现【源码+论文】分享
开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 摘要 信息技术的发展…...

不同类型的电机的工作原理和控制方法汇总
电机控制是指对电机的启动、调速(加速、减速)、运转方向和停止进行的控制,不同类型的电机有着不同的工作原理和控制方法。 一、无刷电机 无刷电机是由电机主体和电机驱动板组成的一种没有电刷和换向器的机电一体化产品。在无刷电机中…...

计算机网络管理 TCP三次握手的建立过程,Wireshark抓包分析并验证TCP三次握手建立连接的报文
⬜⬜⬜ ---🟧🟨🟩🟦🟪 (*^▽^*)欢迎光临 🟧🟨🟩🟦🟪---⬜⬜⬜ ✏️write in front✏️ 📝个人主页:陈丹宇jmu 🎁欢迎各位→…...
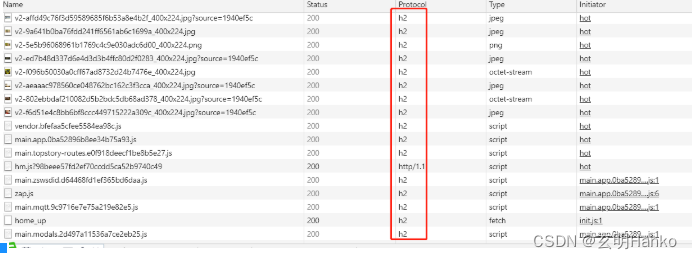
HTTP/2.x:最新的网页加载技术,快速提高您的SEO排名
2.1 http2概念HTTP/2.0(又称HTTP2)是HTTP协议的第二个版本。它是对HTTP/1.x的更新,旨在提高网络性能和安全性。HTTP/2.0是由互联网工程任务组(IETF)标准化的,并于2015年发布。2.2 http2.x与http1.x区别HTTP…...

机器学习----线性回归
第一关:简单线性回归与多元线性回归 1、下面属于多元线性回归的是? A、 求得正方形面积与对角线之间的关系。 B、 建立股票价格与成交量、换手率等因素之间的线性关系。 C、 建立西瓜价格与西瓜大小、西瓜产地、甜度等因素之间的线性关系。 D、 建立西瓜…...
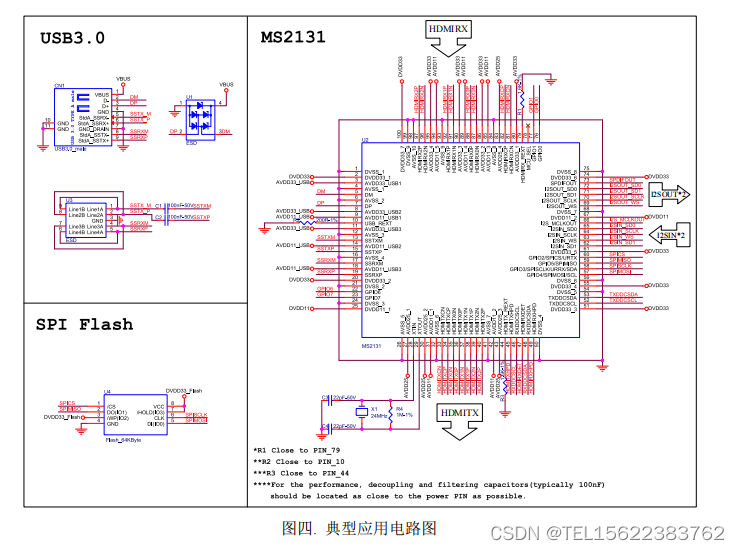
MS2131 USB 3.0 高清音视频采集+HDMI 环出+混音处理芯片 应用网络直播一体机
MS2131 是一款 USB 3.0 高清视频和音频采集处理芯片,内部集成 USB 3.0 Device 控制器、 数据收发模块、音视频处理模块。MS2131 可以通过 USB 3.0 接口将 HDMI 输入的音视频信号传 送到 PC、智能手机、平板电脑上预览或采集。MS2131 支持 HDMI 环出功能,…...

基于堆与AdjustDown的TOP-K问题
TIPSTOP-K问题TOP-K问题:就是说现在比如说有n个数据,然后需要从这n个数据里面找到最大的或最小的前k个。一般来讲思路的话就是:先把这n个数据给他建一个堆,建堆完成之后,然后就去调堆,然后大概只需要调k次&…...
在CentOS上安装Docker引擎
1,先决条件#### 1-1操作系统要求1-2 卸载旧版本 2,安装方法2-1使用存储库安装设置存储库安装 Docker 引擎 本文永久更新地址: 官方地址:https://docs.docker.com/engine/install/centos/ 1,先决条件 #### 1-1操作系统要求 要安装 Docker Engine,您需要…...

【10】核心易中期刊推荐——模式识别与机器学习
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...

【数据结构】并查集
目录 一:用途 二:实现 O(1) 三:例题 例题1:集合 例题2:连通图无向 例题3:acwing 240 食物链 一:用途 将两个集合合并询问两个元素是否在一个集合当中 二:实现 O(1) 每…...

软考--网络攻击分类
网络攻击的主要手段包括口令入侵、放置特洛伊木马程序、拒绝服务(DoS)攻击、端口扫描、网络监听、欺骗攻击和电子邮件攻击等。口令入侵是指使用某些合法用户的账号和口令登录到目的主机,然后再实施攻击活动。特洛伊木马(Trojans)程序常被伪装…...

蓝桥杯刷题冲刺 | 倒计时17天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.长草2.分考场1.长草 题目 链接: 长草 - 蓝桥云课 (lanqiao.cn) 题目描述 小明有一…...

冲击蓝桥杯-并查集,前缀和,字符串
目录 前言 一、并查集 1、并查集的合并(带路径压缩) 2、询问是否为同一个集合 3、例题 二、前缀和 1 、前缀和是什么 2、经典题目 三- 字符串处理 1、字符串的插入 2、字符串转化为int类型 3、字符反转 前言 并查集合前缀,字符串…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...
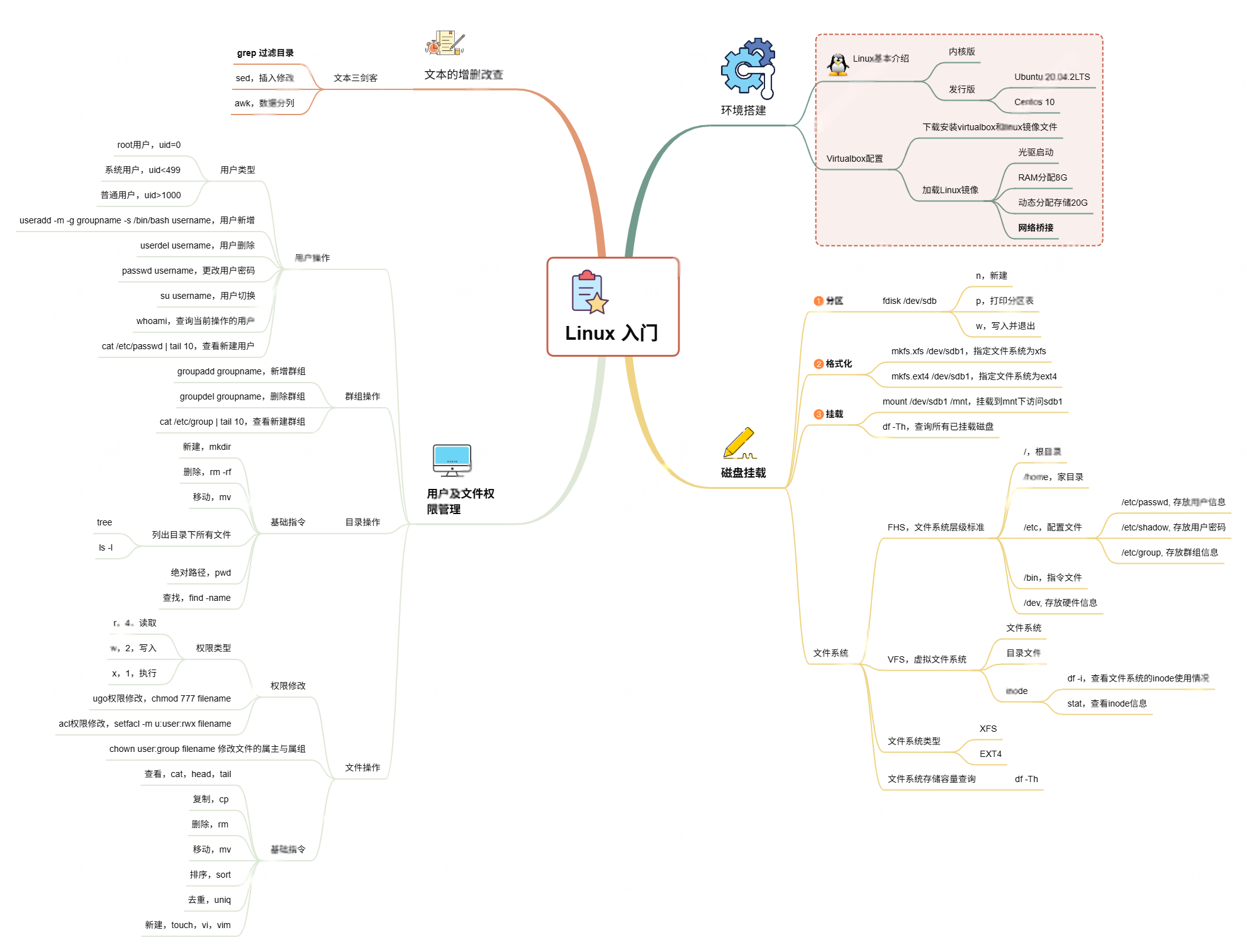
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...

作为点的对象CenterNet论文阅读
摘要 检测器将图像中的物体表示为轴对齐的边界框。大多数成功的目标检测方法都会枚举几乎完整的潜在目标位置列表,并对每一个位置进行分类。这种做法既浪费又低效,并且需要额外的后处理。在本文中,我们采取了不同的方法。我们将物体建模为单…...
