【数据结构】二叉树及相关习题详解
新年新气象! 祝大家兔年 财源滚滚! 万事胜意!
文章目录
- 前言
- 1. 树的一些基础概念
- 1.1 树的一些基本概念
- 1.2 树的一些重要概念
- 2. 二叉树的一些基本概念
- 2.1 二叉树的结构
- 2.2 两种特殊的二叉树
- 3. 二叉树的性质
- 4. 二叉树的存储
- 5. 二叉树的基本操作
- 5.1 构造一棵二叉树
- 5.2 二叉树的遍历
- 5.2.1 前序遍历
- 5.2.2 中序遍历
- 5.2.3 后序遍历
- 5.2.4 层序遍历
- 5.2.# 遍历顺序相关练习题
- 5.3 获取二叉树中节点个数
- 5.4 树中叶子节点个数
- 5.5 反转二叉树
- 5.6 判断树是不是完全二叉树
- 5.7 判断两棵树是否相同
- 5.8 判断一棵树是否为另一颗树的子树
- 5.9 查找值是否存在
前言
二叉树也是笔试中常考的知识点,大家要掌握及时回顾噢~
1. 树的一些基础概念
树是一种非线性的数据结构,它是由n个有限结点组成的一个具有层次关系的集合,像一棵倒挂的树,根在上,叶子在下.
1.1 树的一些基本概念

如上图,是一颗二叉树,因为每个结点最多有两个孩子结点.
以下介绍节点的基本情况
1.根节点: 根节点没有前驱节点
2.叶子节点: 没有孩子结点的节点
3.树中同一棵树的子树与子树之间不能有交集.
4.每棵树除了根节点都只能有一个父亲节点.
5.一棵树如果有N个节点,那么他就有N-1条边.
如下图
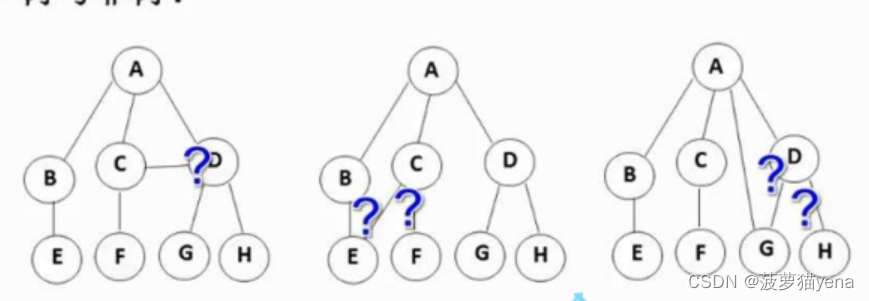
第一个,C与D同是A的子树,C与D之间不能有交集.
第二个,E只能有一个父亲节点,不能有B,C两个父亲节点.
第三个,也是G不能有A,D两个父亲节点.
1.2 树的一些重要概念
1.节点的度: 一个节点含有子树的个数.二叉树中,节点的度可以为0,1,2.叶子结点的度就是0.
2…树的度: 所有节点的度的最大值为树的度
3.结点的层次: 根节点为第一层,依次类推递增
4.树的高度或深度: 树中节点的最大层次为树的高度.
5.兄弟节点: 父亲节点相同的节点互为兄弟节点.
6.节点的子孙: 以该节点为根节点的子树中的任意节点都是该节点的子孙.树中所有节点都是根节点的子孙.
2. 二叉树的一些基本概念
2.1 二叉树的结构
二叉树是节点的有限结合.
二叉树可以为空,也可以只有一个根节点,每个结点最多可以有两个孩子节点.
所以二叉树有以下四种基本情况.
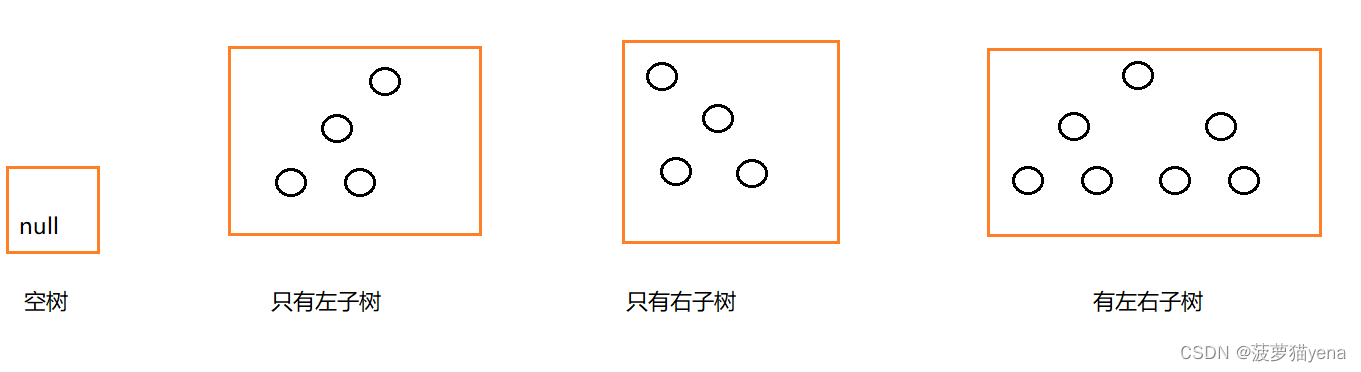
2.2 两种特殊的二叉树
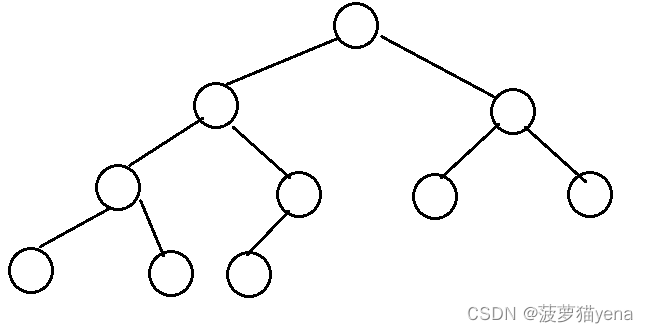
1.满二叉树,如下图,每层的节点都达到最大值.满满登登的.
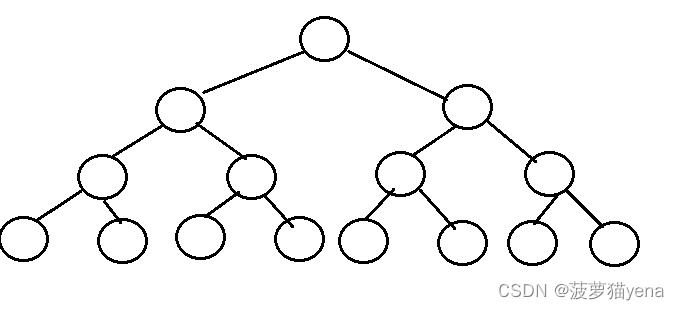
满二叉树,第K层的节点数目为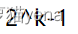
2.完全二叉树,如下图,树从左到右要连续的,从第一个节点到最后一个节点之间不能有为空的节点.
3. 二叉树的性质
1.一棵非空二叉树,以根节点为第一层,第N层节点最大数目为2的n-1次幂.
2.一颗深度为K的非空二叉树,总共节点最大数目为2的K次幂-1.
原理如下,一个深度为4的树,最大节点总数计算过程如下.
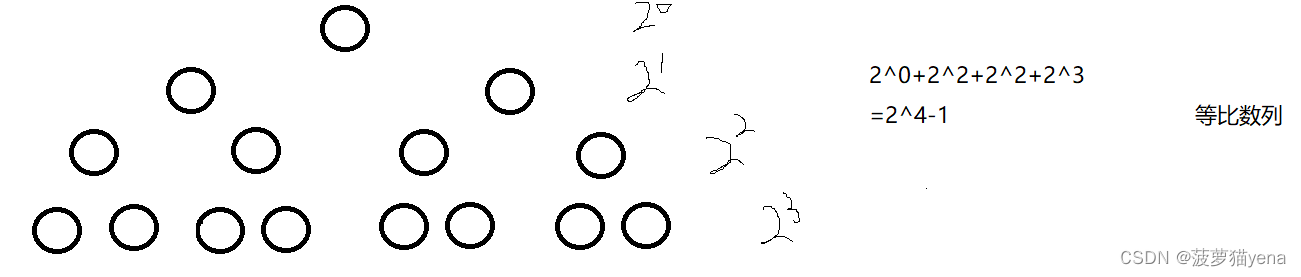
3.一棵二叉树,设其叶子节点个数为n0,度为2(有两个孩子节点)的节点个数为n2,则n0 = n2 + 1.
4.具有N个节点的完全二叉树的深度为log2(n+1)向上取整.
5.若第一个节点从0开始编号,第i个节点(除了根节点),他的父亲节点编号为(i-1)/2.
6.若第一个节点从0开始编号,第i个节点,若它有左右孩子节点,它的左孩子节点编号为2i+1,右孩子编号为2i+2.
例题

解析:
叶子节点为n0,n0 = n2 +1,n0 = 200.

解析:
完全二叉树有如下两种情况.

第一种,节点个数为偶数,只有一个度为1的节点,其余都是度为0和度为2的节点
第二种,节点个数为奇数,全都是度为2和度为0的节点.
本题节点个数为偶数,是第一种情况,只有一个度为1的节点.
节点总数 = n0 + n1 + n2


解析:
这道题与上道题类似,个数为奇数,只有度为0和度为2的节点.
767 = n0 + n2
767 = n0 + n0 -1
n0 = 384

k = log2^(531 +1)
k = 10
4. 二叉树的存储
二叉树可以有顺序存储和链式存储.我们这节先介绍链式存储.
二叉树是由结点和结点与结点之间的的引用构成.
链式存储有二叉三叉表示方法.
第一种是孩子表示法.
class TreeNode{public TreeNode left;//节点左孩子public TreeNode right;//节点右孩子public int value;//节点值
}
第二种是双亲(孩子和父亲)表示法.
class TreeNode{public TreeNode left;public TreeNode right;public TreeNode parent;//节点的父亲节点public int value;
}
本节介绍第一种表示方式.
5. 二叉树的基本操作
5.1 构造一棵二叉树
我们先用简单的方式构造一棵二叉树.
public void createTree(){TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');root = A;A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;}5.2 二叉树的遍历
遍历二叉树根据遍历顺序不同有三种遍历方式: 前序遍历,中序遍历,后序遍历.
5.2.1 前序遍历
前序遍历的顺序为: 根结点->左子树->右子树.
如下图,具体操作是
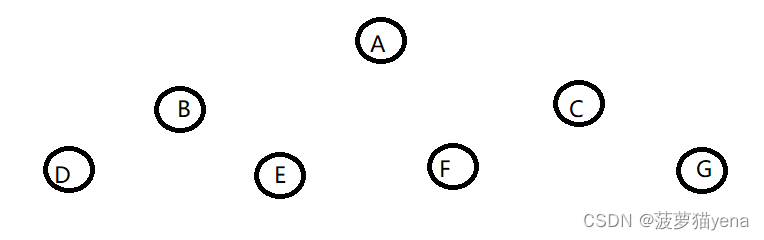
- 先遍历整棵树的根节点A
- 之后遍历根的左子树BDE,如下图,以BDE为一棵树,以根->左->右的顺序,先遍历树的根节点B,再遍历树的左子树D,再遍历树的右子树E.
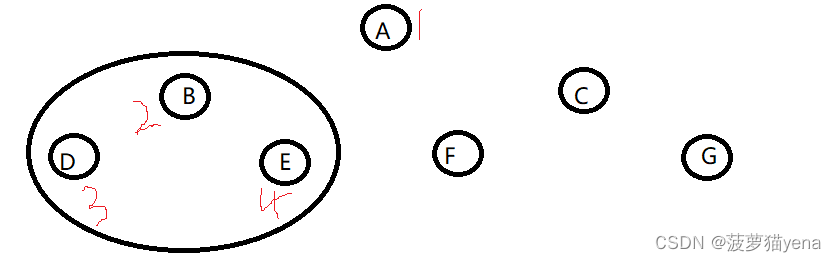
- 遍历根节点的右子树CFG,如下图,先遍历CFG的根节点C,再左子树F,再右子树G
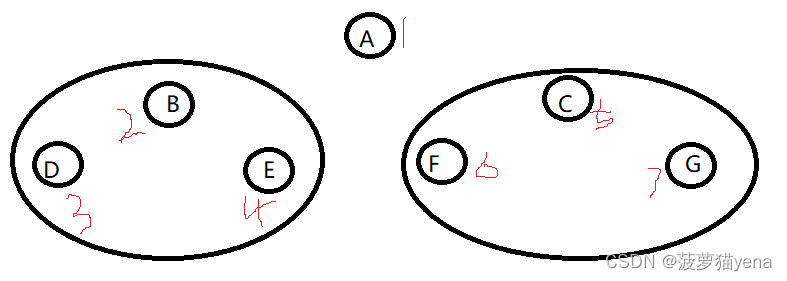
所以,这棵树的前序遍历顺序为ABDECFG.
代码实现
public void preOrder(TreeNode root){//根左右if(root == null){return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}
5.2.2 中序遍历
中序遍历的顺序是左子树->根节点->右子树
- 先找根节点A的左子树BDE,如下图,再根据左->根->右的顺序,以B为根,先遍历B的左子树D,之后是B,再B的右子树E.
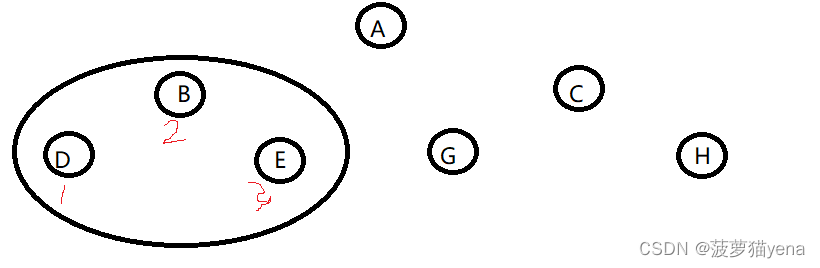
- 遍历完根节点的左子树之后遍历根节点A.
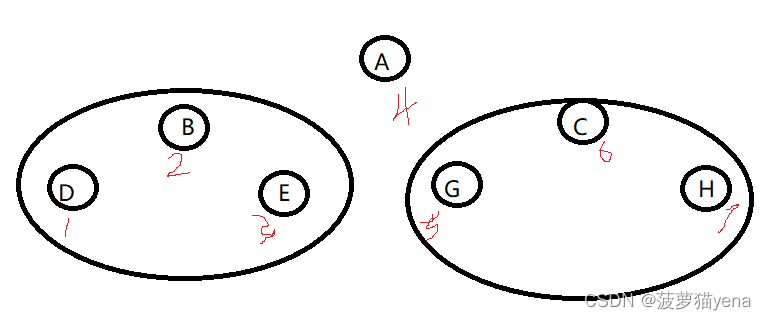
- 之后再以左->根->右的顺序遍历根节点A的右子树.
排好序如下图,这棵树中序遍历为DBEAGCH
代码实现
public void inOrder(TreeNode root){//左根右if(root == null){return;}inOrder(root.left);System.out.print(root.val);inOrder(root.right);}
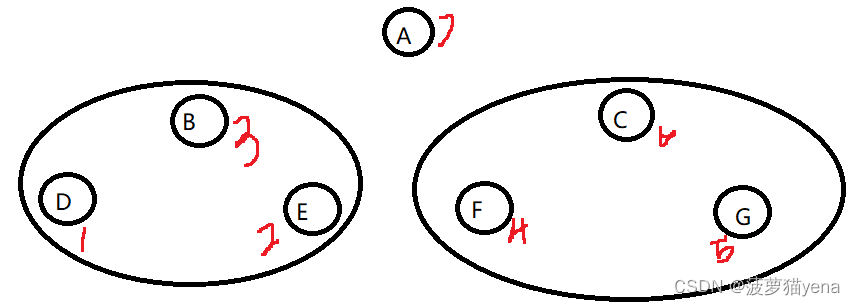
5.2.3 后序遍历
后序遍历的顺序是 左子树->右子树->根
如下图
1.先遍历根节点A的左子树BDE,以B为根节点,以左右根的顺序遍历,结果是DEB.
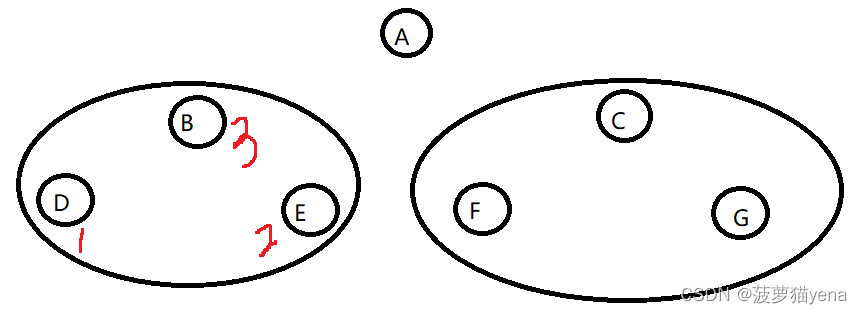
2.左子树遍历完了,再遍历根节点A的右子树CFG,以左右根的顺序,遍历结果为FGC
3.A的左右子树遍历完毕,最后遍历根节点A
如下图,后续遍历顺序为DEBFGCA
代码实现
public void postOrder(TreeNode root){//左右根if(root == null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}
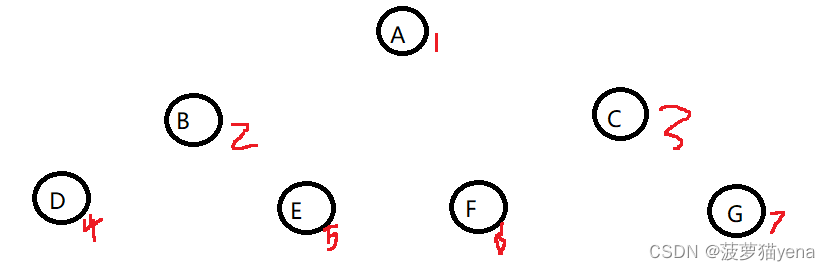
5.2.4 层序遍历
如下图,按照从左到右,从上到下的顺序遍历.遍历顺序为ABCDEFG
5.2.# 遍历顺序相关练习题

解答:树为完全二叉树,中间是没有空缺的树的.所以A是根节点,B是A的左孩子节点,C是A的右孩子节点.
DE分别为B的左右孩子.GH分别为C的左右孩子.所以这棵树前序遍为:ABDHECFG,选A.

解答:很简单哈,先序遍历的第一个节点就是根节点,选A

解答:
1.先看后续节点的倒数第一个节点A,这个节点为根节点.
2.根据中序遍历中根节点的位置,根节点左侧结点为根节点的左子树.根节点右侧结点为根节点的右子树.
3.再看后序遍历的倒数第二个节点C,这是右子树的根.(因为遍历完右子树才会轮到根节点,所以倒数第二节点就是右子树的根)
4.对应中序遍历中C的位置,C的左侧结点为C的左子树,C右侧节点的C的右子树.
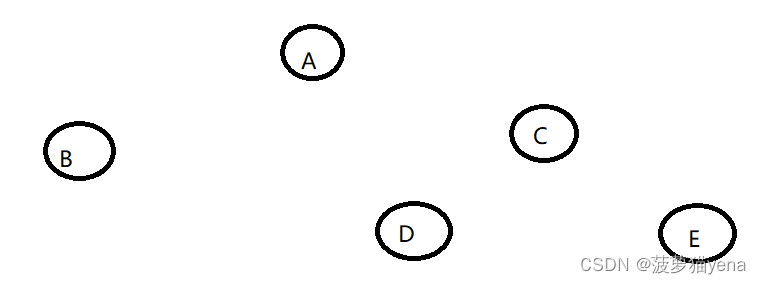
对应这题,后序遍历的最后一个结点是根节点,所以,这颗树的根节点是A.
中序遍历根节点左侧是左子树,根节点右侧是右子树.所以,B是根节点的左子树.
再看后序遍历倒数第二个节点C,它是右子树的根.
对应中序遍历,C的左侧节点是它的左子树.C的右侧节点是他的右子树.所以,D是C的左孩子,E是C的右孩子.
综上,画出二叉树,选D

解答:
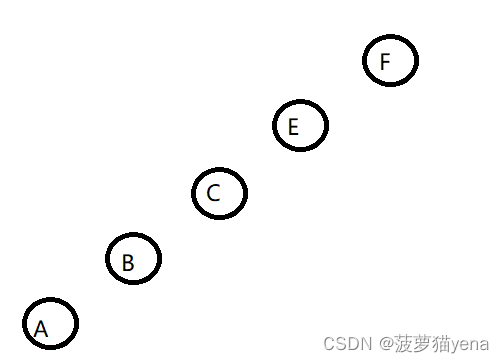
根节点为后序遍历最后一个节点F为根节点
对应中序遍历,F左侧为F的左子树,所以,F只有左子树,无右子树.
因为无右子树,后序遍历倒数第二个节点E为左子树的根节点
对应中序遍历,E的左侧为E的左子树.
以此类推,画出的树如下
层序遍历: FECBA,选A.
5.3 获取二叉树中节点个数
每次的返回值是这个节点左右孩子结点的数量再加上自己的节点,
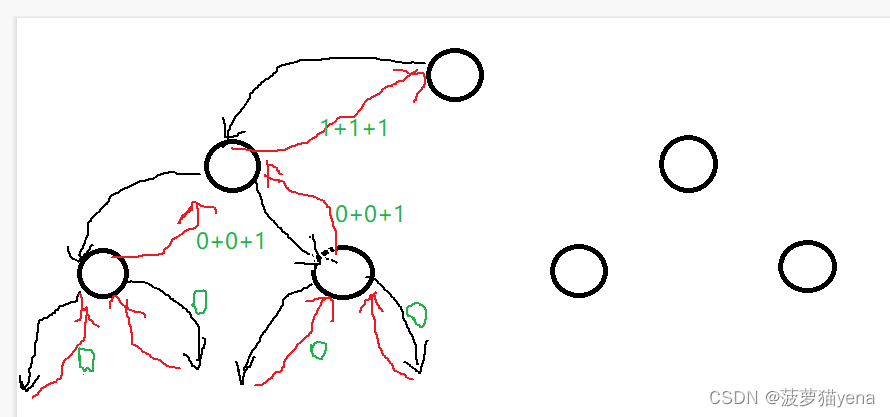
public int nodeCount(TreeNode root){if(root == null){return 0;}int tmp = nodeCount(root.left) + nodeCount(root.right) + 1;return tmp;}
5.4 树中叶子节点个数
树中叶子节点的特点是无左右孩子结点.
与上一题相似,这道题只有符合要求的节点就加1.
public static int LeafNum(TreeNode root){//看节点的左孩子是否为空,再看右孩子是否为空.全部符合则count++.if(root == null){return 0;}int count = 0;if(root.left == null && root.right == null){return 1;}return LeafNum(root.left) + LeafNum(root.right);}
5.5 反转二叉树
反转二叉树,需要将根的左子树与右子树交换,再将每颗小树的左孩子与右孩子交换.
public TreeNode reverseTree(TreeNode root){if(root == null){return null;}TreeNode tmp = root.left;root.left = root.right;root.right = root.left;reverseTree(root.left);reverseTree(root.right);return root;}
5.6 判断树是不是完全二叉树
//判断树是不是完全二叉树public static boolean completeBinaryTree(TreeNode root){if(root == null){return true;}if(root.left == null || root.right == null){return false;}boolean b1 = completeBinaryTree(root.left);boolean b2 = completeBinaryTree((root.right));return b1 && b2;}
5.7 判断两棵树是否相同
//判断两树相同,结构相同,数相同。时间复杂度O( min(r, s) )public static boolean sameTree(TreeNode root1, TreeNode root2){if(root1 == null && root2 != null){return false;}if(root1 != null && root2 == null){return false;}if(root1 == null && root2 == null){return true;}if(root1.val != root2.val){return false;}boolean b = sameTree(root1.left,root2.left);boolean b2 = sameTree(root1.right,root2.right);return b && b2;}
5.8 判断一棵树是否为另一颗树的子树
只要树2等于树1的任意子树就为真
//看树是不是别的树的子树,时间复杂度,O(r * s)public static boolean subtreeJudge(TreeNode root1, TreeNode root2){if(root1 == null || root2 == null){return false;}if(sameTree(root1,root2)){return true;}//注意这里,当root1为空的时候,取不到root1的left,造成空指针异常if(subtreeJudge(root1.left,root2)){return true;}if(subtreeJudge(root1.right,root2)){return true;}return false;}
5.9 查找值是否存在
//查找value是否存在public TreeNode lookupValue(TreeNode root,char val){if(root == null){return null;}if(root.val == val){return root;}TreeNode ret = lookupValue(root.left,val);if(ret != null){return ret;}TreeNode ret2 = lookupValue(root.right,val);if(ret2 != null) {return ret2;}//树的左右结点都走完了,都没找到,返回空return null;}多巩固,多复习.祝前程似锦!
相关文章:

【数据结构】二叉树及相关习题详解
新年新气象! 祝大家兔年 财源滚滚! 万事胜意! 文章目录前言1. 树的一些基础概念1.1 树的一些基本概念1.2 树的一些重要概念2. 二叉树的一些基本概念2.1 二叉树的结构2.2 两种特殊的二叉树3. 二叉树的性质4. 二叉树的存储5. 二叉树的基本操作5.1 构造一棵二叉树5.2 二叉树的遍历…...
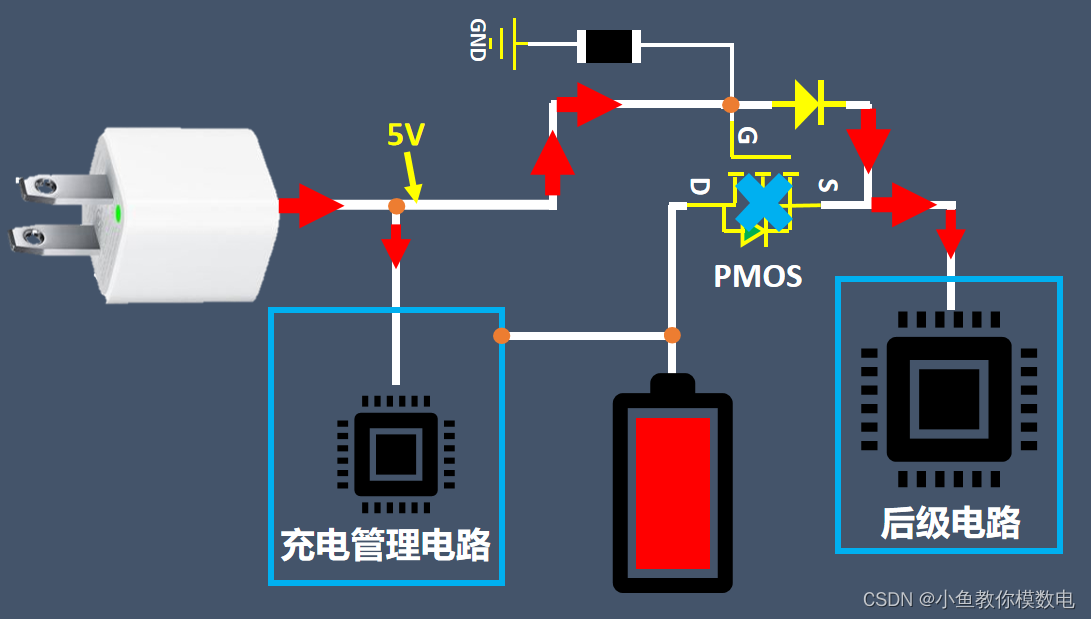
锂电池充电的同时也能放电吗?
大家应该都有这样经历,我们的手机在充电的同时也能边使用,有的同学就会说了,这是因为手机电池在充电的同时也在放电。如果这样想我们可能就把锂电池类比了一个蓄水池,以为它在进水的同时也能出水,其实这个比喻是错误的…...

通信工程考研英语复试专有名词翻译
中文英文频分多址Frequency Division Multiple Access码分多址Code Division Multiple Access时分多址Time Division Multiple Access移动通信mobile communication人工智能artificial intelligence水声通信Middle-Range Uwa Communication正交频分复用Orthogonal frequency di…...

注意力机制(四):多头注意力
专栏:神经网络复现目录 注意力机制 注意力机制(Attention Mechanism)是一种人工智能技术,它可以让神经网络在处理序列数据时,专注于关键信息的部分,同时忽略不重要的部分。在自然语言处理、计算机视觉、语…...

【2023Unity游戏开发教程】零基础带你从小白到超神19——射线检测
文章目录 射线检测从某点发射一条射线从摄像机发射一条射线射线检测 游戏中的红外线,默认肉眼是看不到的,从某个初始点开始,沿着特定的方向发射一条不可见且无限长的射线,通过此射线检测是否有任何模型添加了Collider碰撞器组件。一旦检测到碰撞,停止射线继续发射。 碰撞检…...
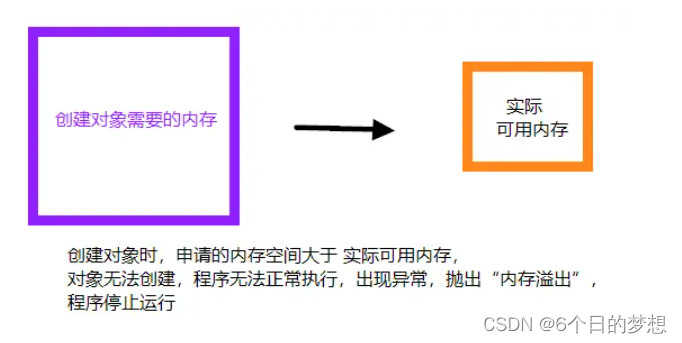
内存泄漏和内存溢出的区别
参考答案 内存溢出(out of memory):指程序在申请内存时,没有足够的内存空间供其使用,出现 out of memory。内存泄露(memory leak):指程序在申请内存后,无法释放已申请的内存空间,内存泄露堆积会导致内存被…...

文本三剑客之sed编辑器
文本三剑客:都是按行读取后处理。 grep 过滤行内容。awk 过滤字段。sed 过滤行内容;修改行内容。sed编辑器 sed是一种流编辑器,流编辑器会在编辑器处理数据之前基于预先提供的一组规则来编辑数据流。 sed编辑器可以根据命令来处理数据流中…...
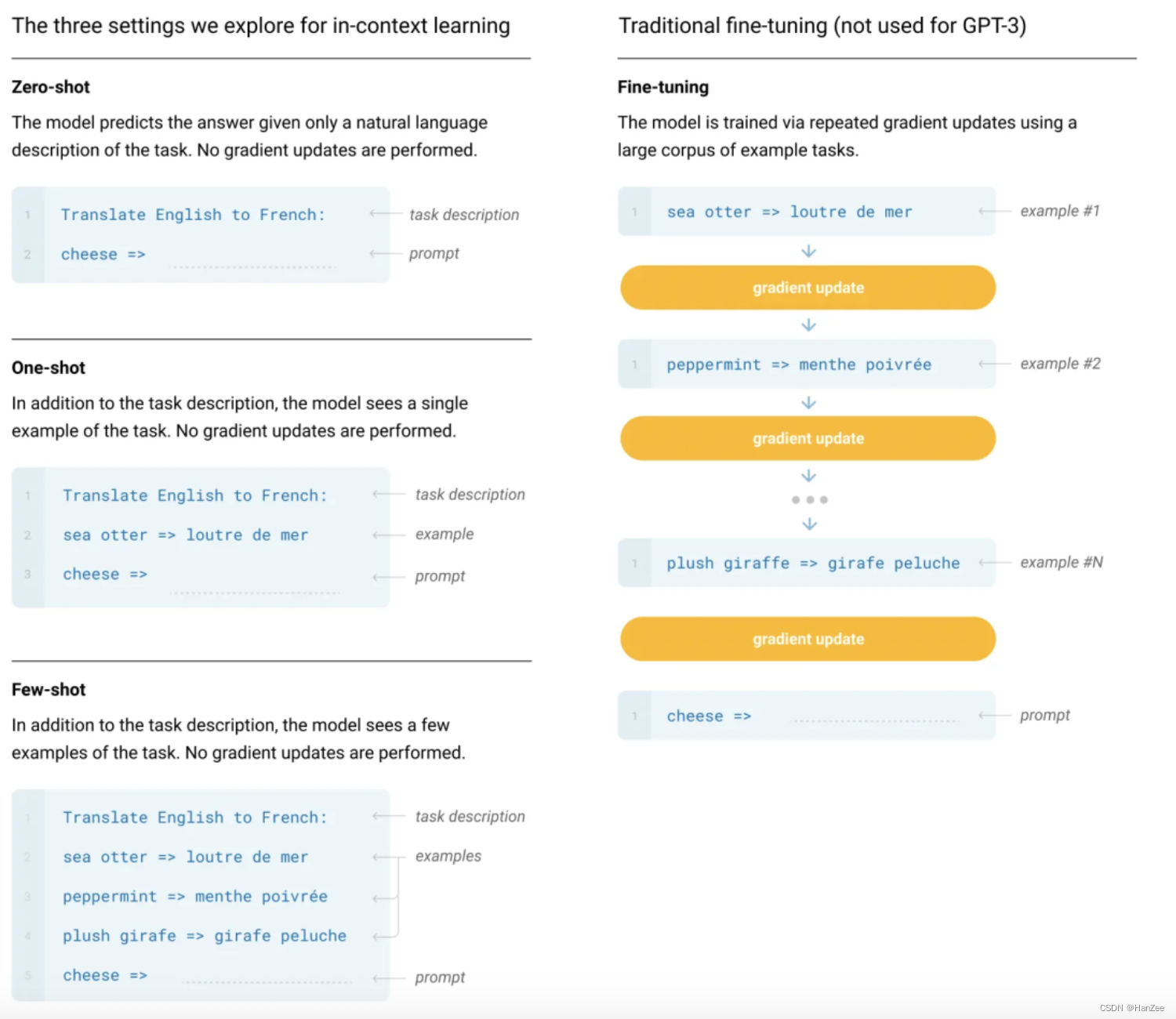
深度学习:GPT1、GPT2、GPT-3
深度学习:GPT1、GPT2、GPT3的原理与模型代码解读GPT-1IntroductionFramework自监督学习微调ExperimentGPT-2IntroductionApproachConclusionGPT-3GPT-1 Introduction GPT-1(Generative Pre-training Transformer-1)是由OpenAI于2018年发布的…...

使用Docker 一键部署SpringBoot和SpringCloud项目
使用Docker 一键部署SpringBoot和SpringCloud项目 1. 准备工作2. 创建Dockerfile3. 创建Docker Compose文件4. 构建和运行Docker镜像5. 验证部署6. 总结Docker是一个非常流行的容器化技术,可以方便地将应用程序和服务打包成容器并运行在不同的环境中。在本篇博客中,我将向您展…...

【数据结构】用栈实现队列
💯💯💯 本篇总结利用栈如何实现队列的相关操作,不难观察,栈和队列是可以相互转化的,需要好好总结它们的特性,构造出一个恰当的结构来实现即可,所以本篇难点不在代码思维,…...
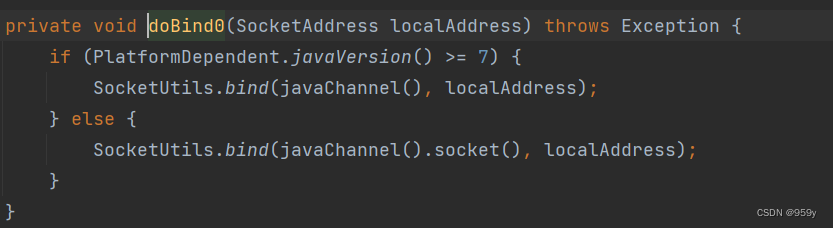
[Netty源码] 服务端启动过程 (二)
文章目录1.ServerBootstrap2.服务端启动过程3.具体步骤分析3.1 创建服务端Channel3.2 初始化服务端Channel3.3 注册selector3.4 端口绑定1.ServerBootstrap ServerBootstrap引导服务端启动流程: //主EventLoopGroup NioEventLoopGroup master new NioEventLoopGroup(); //从E…...

Week 14
代码源每日一题Div2 106. 订单编号 原题链接:订单编号 思路:这题本来没啥思路,直到获得了某位佬的提示才会做( 我们可以用set来维护一些区间,这些区间为 pair 类型,表示没有使用过的编号,每次…...

【微信小程序】-- 使用 Git 管理项目(五十)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

leetcode每日一题:134. 加油站
系列:贪心算法 语言:java 题目来源:Leetcode134. 加油站 题目 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[…...

开放式基金实时排行 API 数据接口
开放式基金实时排行 API 数据接口 多维度参数返回,实时数据,类型参数筛选。 1. 产品功能 返回实时开放式基金排行数据可定义查询基金类型参数;多个基金属性值返回多维指标,一次查询毫秒级返回;数据持续更新与维护&am…...

Android开发中synchronized的实现原理
synchronized的三种使用方式 **1.修饰实例方法,**作用于当前实例加锁,进入同步代码前要获得当前实例的锁。 没有问题的写法: public class AccountingSync implements Runnable{//共享资源(临界资源)static int i0;/*** synchronized 修饰实例方法*/p…...
)
【华为OD机试 2023最新 】 统一限载货物数最小值(C++)
题目描述 火车站附近的货物中转站负责将到站货物运往仓库,小明在中转站负责调度2K辆中转车(K辆干货中转车,K辆湿货中转车)。 货物由不同供货商从各地发来,各地的货物是依次进站,然后小明按照卸货顺序依次装货到中转车,一个供货商的货只能装到一辆车上,不能拆装,但是…...
【生活工作经验 十】ChatGPT模型对话初探
最近探索了下全球大火的ChatGPT,想对此做个初步了解 一篇博客 当今社会,自然语言处理技术得到了迅速的发展,人工智能技术也越来越受到关注。其中,基于深度学习的大型语言模型,如GPT(Generative Pre-train…...

基于Spring Boot房产销售平台的设计与实现【源码+论文】分享
开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 摘要 信息技术的发展…...

不同类型的电机的工作原理和控制方法汇总
电机控制是指对电机的启动、调速(加速、减速)、运转方向和停止进行的控制,不同类型的电机有着不同的工作原理和控制方法。 一、无刷电机 无刷电机是由电机主体和电机驱动板组成的一种没有电刷和换向器的机电一体化产品。在无刷电机中…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
