23.3.26总结
康托展开
是一个全排列与自然数的映射关系,康托展开的实质是计算当前序列在所有从小到大的全排列中的顺序,跟其逆序数有关。
例如:对于 1,2,3,4,5 来说,它的康托展开值为 0*4!+0*3!+0*2!+0*1!
对于 4,3,1,5,2 来说:
3 * 4!+2 * 3!+0 * 2!+1 * 1!+0 * 0!=85
c++中加快读入:
ios_base::sync_with_stdio(0);cin.tie(0); cout.tie(0);//加快读入
红黑树:
是一种高效的查找树,可以在 O(logN)时间内完成查找,增加和删除。
红黑树的平衡过程跟魔方复原非常像,大致过程就是:遇到什么样的节点排布,我们就对应怎么去调整。
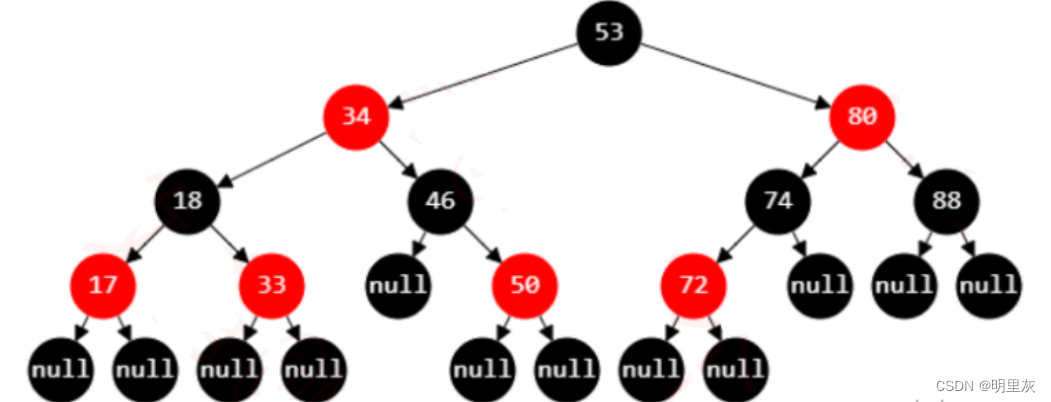
1.节点是红色或黑色,根是黑色
2.叶子节点(外部节点,空节点)都是黑色,这里的叶子节点指的是最底层的空节点(外部节点),下图中的那些null节点才是叶子节点,叶子节点不存储数据,null 节点的父节点在红黑树里不将其看作叶子节点
2.红色节点的子节点都是黑色,红色节点的父节点都是黑色
3.从根节点到叶子节点的所有路径上不能有 2 个连续的红色节点
5.从任一节点到叶子节点的所有路径都包含相同数目的黑色节点
简单搜索&&进阶搜索 - Virtual Judge (vjudge.net)
http://t.csdn.cn/xmPLc
简单搜索&&进阶搜索 - Virtual Judge (vjudge.net)
http://t.csdn.cn/zMf4v
cf补题:
Problem - G2 - Codeforces
http://t.csdn.cn/hWQx5
相关文章:

23.3.26总结
康托展开 是一个全排列与自然数的映射关系,康托展开的实质是计算当前序列在所有从小到大的全排列中的顺序,跟其逆序数有关。 例如:对于 1,2,3,4,5 来说,它的康托展开值为 0*4!0*3!0*2!0*1&…...

【Java学习笔记】37.Java 网络编程
Java 网络编程 网络编程是指编写运行在多个设备(计算机)的程序,这些设备都通过网络连接起来。 java.net 包中 J2SE 的 API 包含有类和接口,它们提供低层次的通信细节。你可以直接使用这些类和接口,来专注于解决问题&…...

Azure OpenAI 官方指南03|DALL-E 的图像生成功能与安全过滤机制
2021年1月,OpenAI 推出 DALL-E。这是 GPT 模型在图像生成方面的人工智能应用。其名称来源于著名画家、艺术家萨尔瓦多 • 达利(Dal)和机器人总动员(Wall-E)。DALL-E 图像生成器,能够直接根据文本描述生成多…...
【数据结构】堆
文章目录前言堆的概念及结构堆初始化堆的判空堆的销毁插入数据删除数据堆的数据个数获取堆顶数据用数组创建堆对数组堆排序有关topk问题整体代码展示写在最后前言 🚩前面了解了树(-> 传送门 <-)的概念后,本章带大家来实现一…...
电脑硬盘文件数据误删除/格式化为什么可以恢复? 怎么恢复?谈谈文件删除与恢复背后的原理
Hello 大家好, 我是元存储~ 主页:元存储的博客_CSDN博客 1. 硬盘数据丢失场景 我们在每天办公还是记录数据的时候,文件存储大多数都是通过硬盘进行存储的,因此,使用多了,各种问题就会出现,比如…...
Gateway服务网关
Spring Cloud Gateway为微服务架构提供一种简单有效的统一的 API 路由管理方式。Gateway网关是所有微服务的统一入口。网关的核心功能特性:请求路由和负载均衡:一切请求都必须先经过gateway,但网关不处理业务,而是根据某种规则&am…...
K8S + GitLab + Jenkins自动化发布项目实践(一)
K8S GitLab Jenkins自动化发布项目实践(一)发布流程设计安装Docker服务部署Harbor作为镜像仓库部署GitLab作为代码仓库常用Git命令发布流程设计 #mermaid-svg-pe9VmFytb9GmqMvG {font-family:"trebuchet ms",verdana,arial,sans-serif;font-…...

【数据结构篇C++实现】- 堆
文章目录🚀一、堆的原理精讲⛳(一)堆的概念⛳(二)看图识最大堆⛳(三)详解堆是用数组表示的树🚀二、堆的向下调整算法🚀三、堆的向上调整算法🚀四、将任意一棵…...

C++笔试题
作用域运算符(::)的作用:1.存在具有相同名称的局部变量时,访问全局变量。2.在类之外定义类相关函数。3.访问类的静态变量。4.在多重继承的情况下,如果两个基类中存在相同的变量名,可以使用作用域运算符来进行区分。5.限定成员函数…...

【Python】基本语法
数据类型 通过 print(type(x)) 可以输出 x 的数据类型,type() 函数可以获取数据类型 整数 a 10 print(type(a)) 浮点数 a 0.5 print(type(a)) 字符串 a hello print(type(a)) 获取字符串长度 a hello print(len(a))字符串拼接 a hello b world prin…...
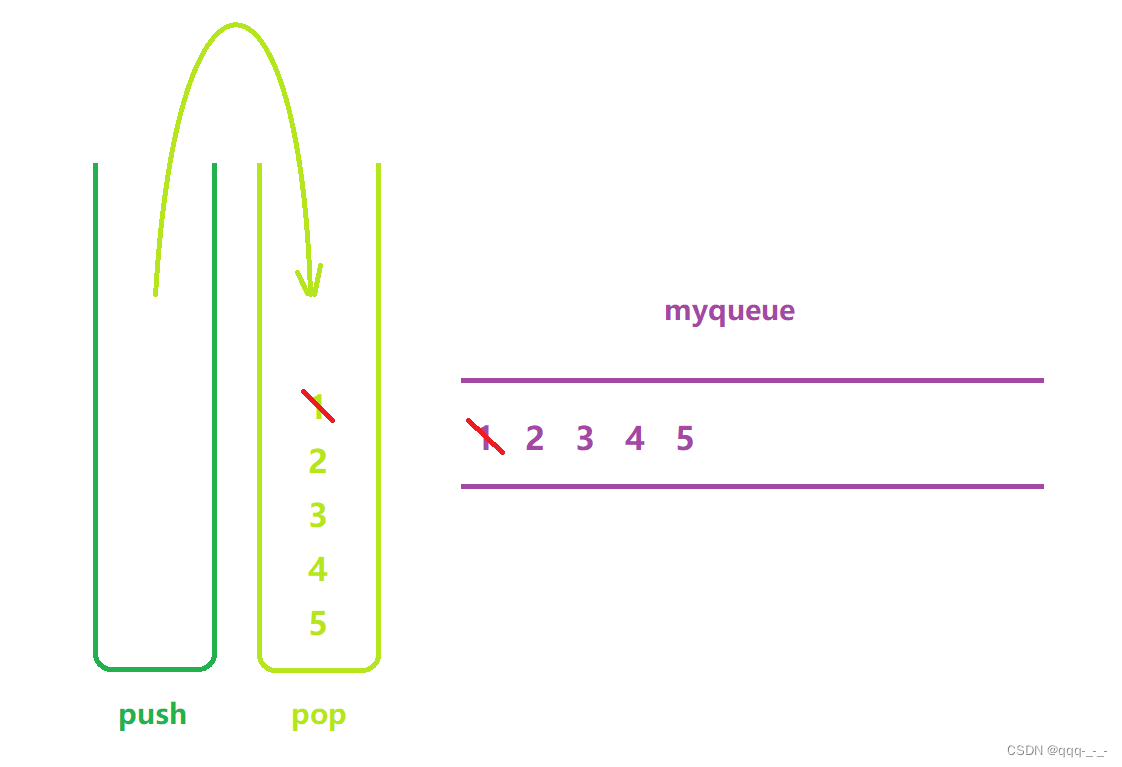
用栈实现队列(图示超详解哦)
全文目录引言用栈实现队列题目介绍思路简述实现栈的部分队列的部分创建队列判断队列是否为空在队列尾入在队列头出访问队头元素释放队列总结引言 在上一篇文章中,我们了解了用两个队列实现栈。在这篇问章中将继续介绍用两个栈实现队列的OJ练习: 用栈实现…...

Spring - Spring 注解相关面试题总结
文章目录01. Spring 配置方式有几种?02. Spring 如何实现基于xml的配置方式?03. Spring 如何实现基于注解的配置?04. Spring 如何基于注解配置bean的作用范围?05. Spring Component, Controller, Repository, Service 注解有何区别…...
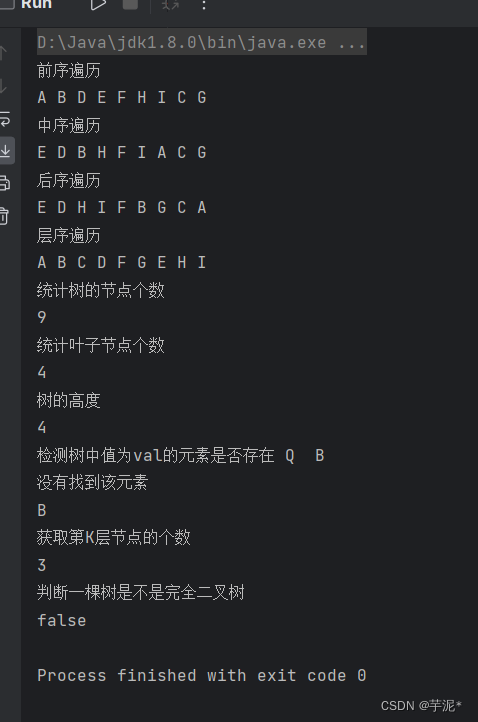
【数据结构】实现二叉树的基本操作
目录 1. 二叉树的基本操作 2. 具体实现 2.1 创建BinaryTree类以及简单创建一棵树 2.2 前序遍历 2.3 中序遍历 2.4 后序遍历 2.5 层序遍历 2.6 获取树中节点的个数 2.7 获取叶子节点的个数 2.8 获取第K层节点的个数 2.9 获取二叉树的高度 2.10 检测值为val的元素是否…...
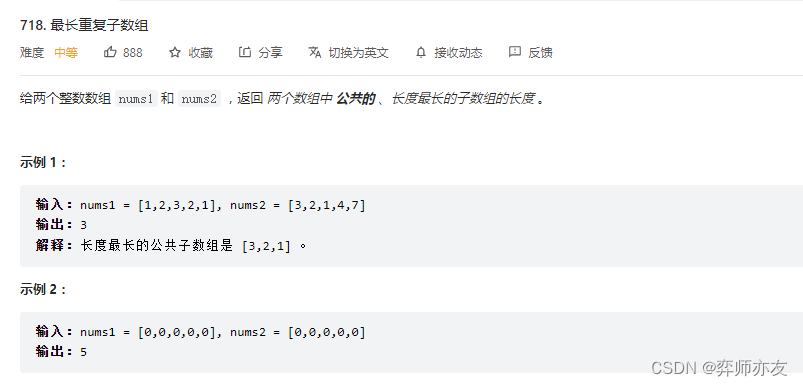
代码随想录算法训练营第五十二天| ● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
300.最长递增子序列 看完题后的思路 dp[i] [0,i]子数组中,以nums[i]结尾的子序列的长度 dp[i]dp[j]1 j从i-1向0遍历,在所有nums[j]<nums[i]中dp[j]最大 初始化 dp[0]1 代码 class Solution {public int lengthOfLIS(int[] nums) {if (nums.length0){return 0;}int[] dpne…...

手机验证发送及其验证(基于springboot+redis)保姆级
在Java开发中,发送手机验证码时需要考虑以下几个问题: 验证码的有效期:验证码应该有一定的有效期,一般设置为几分钟或者十几分钟。过期的验证码应该被认为是无效的,不能用于验证用户身份。手机号码格式的校验…...

【JavaScript 逆向】数美滑块逆向分析
声明本文章中所有内容仅供学习交流,相关链接做了脱敏处理,若有侵权,请联系我立即删除!案例目标验证码:aHR0cHM6Ly93d3cuaXNodW1laS5jb20vbmV3L3Byb2R1Y3QvdHcvY29kZQ以上均做了脱敏处理,Base64 编码及解码方…...

多任务之线程
文章目录一、多任务是什么?二、多任务-线程四、通过继承Tread类完成创建线程五、资源竞争六、同步与互斥锁七、对峙与避免死锁一、多任务是什么? 多个函数同时执行一件事情就是多任务,没有多任务的时候任务执行都是按照顺序的,而…...
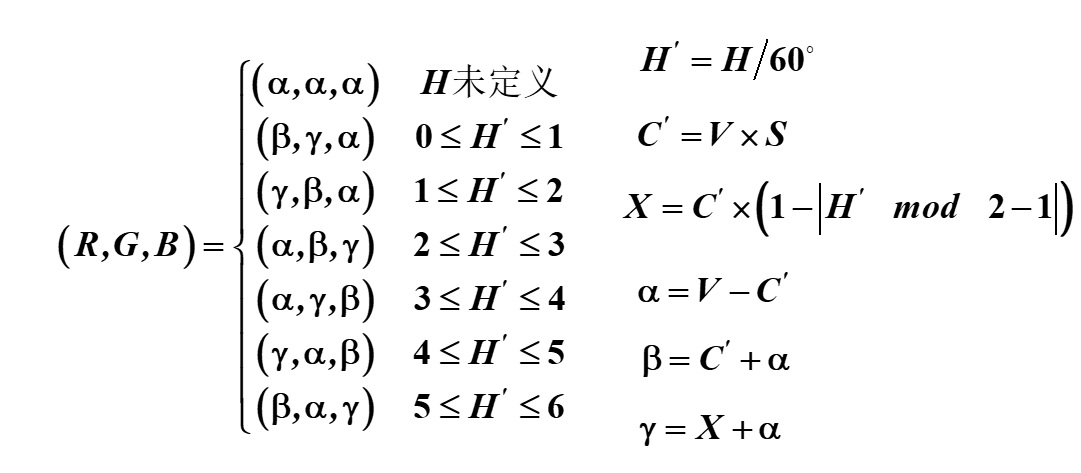
(数字图像处理MATLAB+Python)第二章数字图像处理基础-第二节:色度学基础与颜色模型
文章目录一:颜色匹配二:CIE 1931-RGB系统三:CIE 1931标准色度系统四:CIE 1976Lab均匀颜色空间五:孟塞尔表色系统(1)孟塞尔明度(Value,记为V)(2)孟塞尔彩度(Ch…...
)
【华为OD机试 2023最新 】 网上商城优惠活动(C++)
文章目录 题目描述输入描述输出描述备注用例题目解析C++题目描述 某网上商场举办优惠活动,发布了满减、打折、无门槛3种优惠券,分别为: 每满100元优惠10元,无使用数限制,如100199元可以使用1张减10元,200299可使用2张减20元,以此类推;92折券,1次限使用1张,如100元,…...

记一次CentOS 8 部署packstack部署OpenStack失败案例,请直接看最后
首先你需要一台安装好CentOS8 的虚拟机,相关参数如图。两块网卡,网卡1 NAT IP 192.168.100.100 GW192.168.100.2 网卡2 可不做配置。能ping通百度。创建完成虚拟机记得打好快照。 开机编辑基本配置环境变量 [rootlocalhost ~]# nmcli connection show NA…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...
