flume--数据从kafka到hdfs发生错误

解决:
#1.将flume自带的依赖删除
mv /opt/installs/flume1.9/lib/guava-11.0.2.jar /opt/installs/flume1.9/lib/guava-11.0.2.jar.bak
#2.将hadoop的依赖发送到flume下
cp /opt/installs/hadoop3.1.4/share/hadoop/common/lib/guava-27.0-jre.jar /opt/installs/flume1.9/lib/相关文章:

flume--数据从kafka到hdfs发生错误
解决: #1.将flume自带的依赖删除 mv /opt/installs/flume1.9/lib/guava-11.0.2.jar /opt/installs/flume1.9/lib/guava-11.0.2.jar.bak #2.将hadoop的依赖发送到flume下 cp /opt/installs/hadoop3.1.4/share/hadoop/common/lib/guava-27.0-jre.jar /opt/installs/f…...
)
Android笔试面试题AI答之Kotlin(14)
文章目录 64. Kotlin中定义函数还是属性场景?使用属性的场景使用函数的场景示例 65. 阐述Kotlin中变量初始化有几种?其中lateinit、by lazy、delegates.notNull有什么区别 ?Kotlin中变量初始化的几种方式lateinit、by lazy、Delegates.notNull的区别 66. Kotlin中…...

博弈论,CF 1600E - Array Game
目录 一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 二、解题报告 1、思路分析 2、复杂度 3、代码详解 一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 1600E - Array Game 二、解题报告 1、思路分析 记最长递增前缀长度为L&a…...

win10安装docker,打包python、java然后centos执行镜像
一、win10安装Docker Desktop docker官网(需要魔法)下载:https://www.docker.com/products/docker-desktop/ 安装方法参考:https://blog.csdn.net/beautifulmemory/article/details/137970794 下载完毕后界面安装,不勾…...

【数据结构入门】二叉树之堆的实现
文章目录 前言一、树1.1 树的概念1.2 树的相关概念 二、二叉树2.1 二叉树的概念2.2 特殊的二叉树2.3 二叉树的性质 三、堆3.1 堆的概念3.2 堆的性质3.3 堆的存储3.4 堆的实现3.4.1 堆的初始化3.4.2 堆的销毁3.4.1 堆向上调整算法3.4.2 堆向下调整算法3.4.3 堆的创建3.4.4 堆的插…...
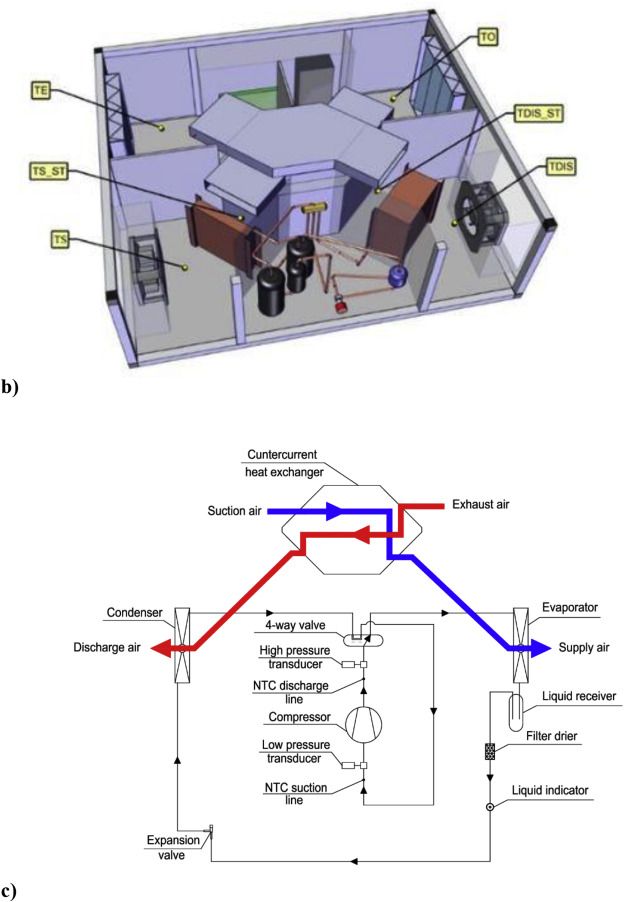
智能微气候:精准调控背后的算法革命
( 于景鑫 国家农业信息化工程技术研究中心)当人工智能遇见现代农业,会擦出怎样的火花?随着数字农业、智慧农业的蓬勃发展,人工智能技术正以前所未有的速度渗透到农业生产的方方面面。其中,以深度学习为代表的前沿算法,尤其是大语言模型(LLM),正在成为驱…...

eNSP 华为交换机链路聚合
华为交换机链路聚合 链路聚合好处: 1、提高带宽 2、链路冗余 SW_2: <Huawei>sys [Huawei]sys SW_2 [SW_2]vlan batch 10 20 [SW_2]int g0/0/4 [SW_2-GigabitEthernet0/0/4]port link-type access [SW_2-GigabitEthernet0/0/4]port default vl…...

编译器揭秘
从上世纪50年代开始,编程语言五花八门,编译器和解释器层出不穷。此处只列出常见编程语言的编译器和解释器信息,不常见的编程语言有单独文章介绍。 C/C cc 此处代表Unix C编译器,其他平台可能借用cc软链接到真正的C编译器。MSVC 微…...

ubuntu下qt连接mysql出现 QMYSQL driver not loaded
1、首先检查是否重新安装了MySQL的驱动,可以使用命令: sudo apt-get remove libqt5sql5-mysql sudo apt-get install libqt5sql5-mysql 2、重新安装ibmysqlclient-dev即可解决 sudo apt-get remove libmysqlclient-dev sudo apt-get install libmysq…...

html 首行缩进2字符
1. html 首行缩进2字符 1.1. 场景 在Html开发中让一段文字(富文本等)首行缩进两个文字,可能在前面加上8个“ ”,因为过去对CSS不熟悉,这种方法实现虽然比较直接,但是文字多的时候会有很多“ ”充斥在代码中…...

什么是IP?
目录 简介 IP IP协议 IP地址 发展历程 IP地址类型 公有地址 私有地址 IP地址编址方式 A类IP地址 B类IP地址 C类IP地址 D类IP地址 特殊的网址 子网 超网 无类间路由 IP地址的分配 IP地址管理 手工管理模式 DHCP分配IP地址的管理模式 通过交换机管理IP 地址…...

js拖拽交换元素位置
摘要:最近在做会议系统,9宫格小画面要支持拖拽调整顺序,需求已经实现了,简单记录下当时的逻辑处理。 /* 关于拖拽逻辑处理 start */ // 当前在拖动的下标 const curDragIndex useRef<number>(-1); /* 拖拽元素事件* onDragStart_开始* onDragend_结束 */ const handleD…...

在 C++ 中实现自定义容器的实用指南
在 C 中实现自定义容器的实用指南 在 C 编程中,容器是存储和管理数据的基本工具。标准库提供了多种容器,如 std::vector、std::list 和 std::map,但在某些情况下,开发者可能需要实现自定义容器以满足特定需求。本文将详细介绍如何…...

《深入浅出WPF》读书笔记.4名称空间详解
《深入浅出WPF》读书笔记.4名称空间详解 背景 主要讲明名称空间概念,可以理解为命名空间的引用。 xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml" 👆如x可以理解为一些列命名空间的引用。 不一一列举,只讲几个特殊的…...

电驱动总成
电驱动总成(Electric Drive Assembly)是电动汽车和混合动力汽车中关键的组成部分,主要负责将电能转化为机械能,以驱动汽车的轮胎。电驱动总成包括多个关键组件,通常可以分为以下几个主要部分: ### 主要组成…...

JavaScript class和正则
正则表达式练习 出生日期 年 月 日 ()表示一个整体 console.log(1909.match(^19\\d{2}$)); console.log(2024.match(^20(([01][0-9])|(2[0-4]))$)); //年 console.log(1909.match(^(19\\d{2})|(20(([01][0-9])|(2[0-4])))$)); // 月 console.log(12.match(^(0[1-9])|(1[0-2])…...
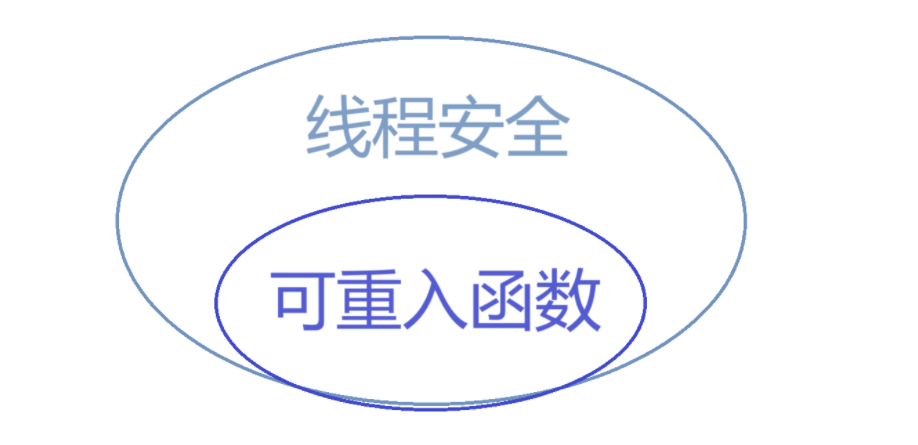
[Linux#42][线程] 锁的接口 | 原理 | 封装与运用 | 线程安全
互斥量 mutex • 大部分情况,线程使用的数据都是局部变量,变量的地址空间在线程栈空间 内,这种情况,变量归属单个线程,其他线程无法获得这种变量。 • 但有时候,很多变量都需要在线程间共享,这…...

奇异递归Template有啥奇的?
如果一个模版看起来很头痛,那么大概率这种模版是用来炫技,没啥用的,但是CRTP这个模版,虽然看起来头大,但是却经常被端上桌~ 奇异递归模板模式(Curiously Recurring Template Pattern, CRTP)是一…...

每天五分钟深度学习框架pytorch:神经网络工具箱nn的介绍
本文重点 我们前面一章学习了自动求导,这很有用,但是在实际使用中我们基本不会使用,因为这个技术过于底层,我们接下来将学习pytorch中的nn模块,它是构建于autograd之上的神经网络模块,也就是说我们使用pytorch封装好的神经网络层,它自动会具有求导的功能,也就是说这部…...

【办公软件】安全风险 Microsoft 已阻止宏运行,因为此文件的来源不受信任
Excel 2019版本,就出现安全风险 Microsoft 已阻止宏运行 因为此文件的来源不受信任的问题,宏直接就用不了了。 网上的解决方法,文件右键属性->取消安全锁。但存在没有安全锁这个选项。后查询到一个简单的解决方法。 打开Excel表格->文件…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
