数学生物学-2-离散时间模型(Discrete Time Models)
上一篇介绍了一个指数增长模型。然而,我们也看到,在现实情况下,细菌培养的增长是在离散的时间(在这种情况下是小时)进行测量的,种群并没有无限增长,而是趋于以S形曲线趋于平稳,称为“逻辑曲线”。
数学生物学-1-指数增长与衰退(Exponential Growth and Decay)-CSDN博客
这里发生的是,由于培养基中食物数量有限,细菌细胞由于竞争食物而生长减缓,因此,种群也开始以更慢的速度增长,越来越趋于稳定。
在本篇中,我们将提出一个描述这种增长的一般模型以及两个替代模型。 数学上,这个过程可以用所谓的“离散逻辑模型”来描述。这是一个类似于之前表达的方程式的形式:

其中r是繁殖率常数,K是模型的承载能力。如之前所示,指数增长模型在生物学上是不现实的,因为它显示了无限增长。正如我们将看到的,离散逻辑模型纳入了一个承载能力,防止了无限增长。带有N^2t的项代表了种群内的种内竞争。
这其实可以表示为一个微分方程:
我们假定r=1.5,N=100,使用R语言求解微分方程得:
# 加载所需的包
library(deSolve)# 定义逻辑斯蒂增长模型
logistic_growth <- function(time, state, parameters) {with(as.list(c(state, parameters)), {dN <- r * N * (1 - N/K)return(list(dN))})
}# 初始条件和参数
state <- c(N = 10) # 初始菌群数量
parameters <- c(r = 1.5, K = 100) # 增长率和承载能力# 时间向量
times <- seq(0, 50, by = 0.1)# 求解微分方程
out <- ode(y = state, times = times, func = logistic_growth, parms = parameters)# 绘制菌群增长曲线
library(ggplot2)
ggplot(data.frame(out), aes(x = time, y = N)) +geom_line() +labs(x = "Time", y = "Population Size", title = "Logistic Growth of Bacterial Population") +theme_minimal()
对离散逻辑函数的增强
我们应该注意到,离散逻辑方程的实现会遇到一个问题,即当N的值较大时,会给出一个负值。当然,也有其他形式的离散逻辑方程,如de Vries等人(2006)所建议的,可以解决这个问题。
方案一:Beverton-Holt模型
选项I 其中一个替代模型是所谓的Beverton-Holt模型(Beverton和Holt 1993;Geritz和Kisdi 2004),该模型是为渔业而推导出来的,用以下离散逻辑方程代替:

with r > 1 and (of course) K > 0. Note Nt+1 > 0 for all t.
方案二:Ricker模型
另一个模型是所谓的Ricker模型(Ricker 1954;Geritz和Kisdi 2004),也是为渔业而推导出来的,用以下离散逻辑方程代替:

with r > 1 and K > 0. Again, note that Nt+1 > 0 for all t.
我们分别可视化看一下:
library(ggplot2)# 参数设置
r <- 1.5
K <- 100
N <- seq(0, K, length.out = 100)# 离散逻辑模型(DLM)
g_DLM <- r * N * (1 - N/K)# Beverton-Holt模型(B-H)
g_BH <- N * (1 - N/K)^r# Ricker模型
g_Ricker <- N * exp(r * (1 - N/K))# 创建数据框
df <- data.frame(N = N, g_DLM = g_DLM, g_BH = g_BH, g_Ricker = g_Ricker)# 绘制图形
p <- ggplot(df, aes(x = N)) +geom_line(aes(y = g_DLM, color = "Discrete Logistic Model"), linewidth = 1) +geom_line(aes(y = g_BH, color = "Beverton-Holt Model"), linewidth = 1) +geom_line(aes(y = g_Ricker, color = "Ricker Model"), linewidth = 1) +scale_color_manual(name = "Model",values = c("Discrete Logistic Model" = "blue","Beverton-Holt Model" = "red","Ricker Model" = "green")) +labs(title = "Growth Functions for Discrete Models",x = "Population Size (N)",y = "Growth Rate",caption = "r = 1.5, K = 100") +theme_minimal() +theme(text = element_text(size = 12),plot.caption = element_text(hjust = 0.95))# 显示图形
print(p)
或者可以可视化为:

这三种模型都可以用一个生长函数来表达,形式如下:

如果我们观察生长函数 g(N) 依赖于 N 的方式,我们可以看到离散逻辑模型导致 Nt+1 为负的问题是如何产生的,而对于 Beverton-Holt 和 Ricker 模型则不会。请注意,图中所有三个函数都在 N = K(此图中为 100)处相交,此时生长函数等于 1.0。
总结
离散逻辑模型通过引入一个承载能力来解决第章中提出的简单指数增长模型的问题,该承载能力防止种群无限增长。另一方面,离散逻辑模型有一个弱点,即当 N 的值足够大时,下一个计算出的种群大小将为负。Beverton-Holt 和 Ricker 等替代模型通过使用不会变为负数的生长函数来解决这个弱点。
相关文章:

数学生物学-2-离散时间模型(Discrete Time Models)
上一篇介绍了一个指数增长模型。然而,我们也看到,在现实情况下,细菌培养的增长是在离散的时间(在这种情况下是小时)进行测量的,种群并没有无限增长,而是趋于以S形曲线趋于平稳,称为“…...
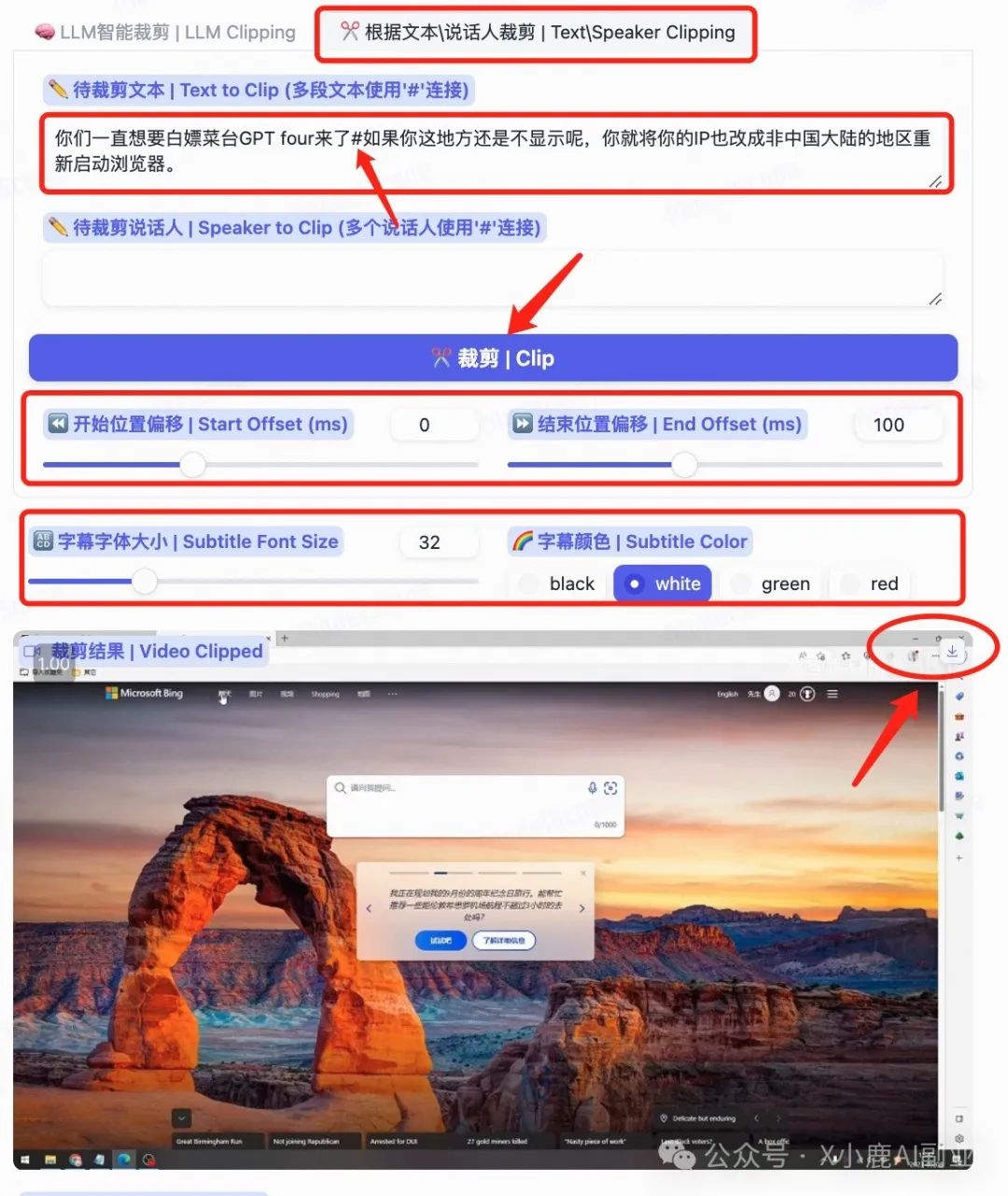
免费开源!AI视频自动剪辑已成现实!效率提升80%,打工人福音!(附详细教程)
大家好,我是程序员X小鹿,前互联网大厂程序员,自由职业2年,也一名 AIGC 爱好者,持续分享更多前沿的「AI 工具」和「AI副业玩法」,欢迎一起交流~ 想象一下,假设老板给你布置了一项任务:…...

NtripShare全站仪自动化监测之气象改正
最近有幸和自动化监测领域权威专家进行交流,讨论到全站仪气象改正的问题,因为有些观点与专家不太一致,所以再次温习了一下全站仪气象改正的技术细节。 气象改正的概念 全站仪一般利用光波进行测距,首先仪器会处理测距光波的相位漂…...

【人工智能】项目案例分析:使用自动编码器进行信用卡欺诈检测
一、项目背景 信用卡欺诈是金融行业面临的一个重要问题,快速且准确的欺诈检测对于保护消费者和金融机构的利益至关重要。本项目旨在通过利用自动编码器(Autoencoder)这一无监督学习算法,来检测信用卡交易中的欺诈行为,…...

【工控】线扫相机小结
背景简介 我目前接触到的线扫相机有两种形式: 无采集卡,数据通过网线传输。 配备采集卡,使用PCIe接口。 第一种形式的数据通过网线传输,速度较慢,因此扫描和生成图像的速度都较慢,参数设置主要集中在相机本身。第二种形式的相机配备采集卡,通常速度更快,但由于相机和…...

将Web应用部署到Tomcat根目录的三种方法
将应用部署到Tomcat根目录的三种方法 将应用部署到Tomcat根目录的目的是可以通过"http://[ip]:[port]"直接访问应用,而不是使用"http://[ip]:[port]/[appName]"上下文路径进行访问。 方法一:(最简单直接的方法࿰…...

工业和信息化部教育与考试中心计算机相关专业介绍
国家工信部的认证证书在行业内享有较高声誉。 此外,还设有专门的工业和信息化技术技能人才数据库查询服务,进一步方便了个人和企业对相关职业能力证书的查询需求。 序号 专业工种 级别 备注 1 JAVA程序员 初级 职业技术 2 电子…...

第二证券:生物天然气线上交易达成 创新探索互联互通、气证合一
8月20日,上海石油天然气生意中心在国内立异推出生物天然气线上生意。当日,绿气新动力(北京)有限公司(简称“绿气新动力”)挂单的1500万立方米生物天然气被百事食物(我国)有限公司&am…...

重磅!RISC-V+OpenHarmony平板电脑发布
仟江水商业电讯(8月18日 北京 委托发布)RISC-V作为历史上全球发展速度最快、创新最为活跃的开放指令架构,正在不断拓展高性能计算领域的边界。OpenHarmony是由开放原子开源基金会孵化并运营的开源项目,已成为发展速度最快的智能终…...
[DL]深度学习_扩散模型
扩散模型原理 深入浅出扩散模型 一、概念简介 1、Denoising Diffusion Probalistic Models,DDPM 1.1 扩散模型运行原理 首先sample一个都是噪声的图片向量,这个向量的shape和要生成的图像大小相同。通过Denoise过程来一步一步有规律的滤去噪声。Den…...

AI学习记录 - 如何快速构造一个简单的token词汇表
创作不易,有用的话点个赞 先直接贴代码,我们再慢慢分析,代码来自openai的图像分类模型的一小段 def bytes_to_unicode():"""Returns list of utf-8 byte and a corresponding list of unicode strings.The reversible bpe c…...

JAVA中的数组流ByteArrayOutputStream
Java 中的 ByteArrayOutputStream 是一个字节数组输出流,它允许应用程序以字节的形式写入数据到一个字节数组缓冲区中。以下是对 ByteArrayOutputStream 的详细介绍,包括其构造方法、方法、使用示例以及运行结果。 一、ByteArrayOutputStream 概述 Byt…...

S3C2440中断处理
一、中断处理机制概述 中断是CPU在执行程序过程中,遇到急需处理的事件时,暂时停止当前程序的执行,转而执行处理该事件的中断服务程序,并在处理完毕后返回原程序继续执行的过程。S3C2440提供了丰富的中断源,包括内部中…...

《数据分析与知识发现》
《数据分析与知识发现》介绍 1 期刊定位 《数据分析与知识发现》(Data Analysis and Knowledge Discovery)是由中国科学院主管、中国科学院文献情报中心主办的学术性专业期刊。期刊创刊于2017年,由《现代图书情报技术》(1985-20…...
IaaS,PaaS,aPaaS,SaaS,FaaS,如何区分?
IaaS, PaaS,SaaS,aPaaS 还有一种 FaaS ,这几个都是云服务中常见的 5 大类型: IaaS:基础架构即服务,Infrastructure as a Service PaaS:平台即服务,Platform as a Service aPaaS&…...

软件测试工具分享
要想在测试中旗开得胜,趁手的“武器”那是相当重要(说人话,要保证测试质量和效率,测试工具也很重要)。现在,小酋打算亮一亮自己的武器库,希望不要闪瞎你的眼(天上在打雷,…...
word翻译工具有哪些?5个工具助你快速翻译Word文件
无论是商业沟通还是文化交流,都需要跨越语言障碍。而文档翻译则是这一过程中的重要环节之一。 想象一下,当你需要将一份重要的Word文档从一种语言翻译成另一种语言时,如果手动逐句翻译不仅耗时耗力,还可能因为文化差异导致误解。…...

【51单片机】ds18b20驱动,11.0592MHZ,使用DS18b20
文章目录 ds18b20.h #include <reg52.h> #include <intrins.h> #include <math.h>// 管脚定义 sbit DS18B20_DATA_PIN = P1 ^ 0; // DS18B20数据口定义/******************************************************************************* * 函 数 名 …...

Vue 导航条+滑块效果
目录 前言代码效果展示导航实现代码导航实现代码导航应用代码前言 总结一个最近开发的需求。设计稿里面有一个置顶的导航条,要求在激活的项目下面展示个下划线。我最先开始尝试的是使用 after 的伪类选择器,直接效果一样,但是展示的时候就会闪现变化,感觉不够自然,参考了一…...

Android:使用Gson常见问题(包含解决将Long型转化为科学计数法的问题)
一、解决将Long型转化为科学计数法的问题 1.1 场景 将一个对象转为Map类型时,调用Gson.fromJson发现,原来对象中的long类型的personId字段,被解析成了科学计数法,导致请求接口失败,报参数错误。 解决结果图 1.2、Exa…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...

Selenium 查找页面元素的方式
Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素,以下是主要的定位方式: 基本定位方式 通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...
