第1节 线性回归模型
1. 模型概述
对于收集到的数据(xi,yi)(x_i,y_i)(xi,yi),建立线性回归模型yi=θTxi+εi(1)y_i=\theta^{^T} x_i +\varepsilon_i (1)yi=θTxi+εi(1)
需要估计的参数为θT\theta^{^T}θT,我们的目的是让估计的参数θT\theta^{^T}θT和xix_ixi组合后,得到的估计值y^i\hat{y}_iy^i与实际值yiy_iyi越接近越好,也就是随机误差项εi\varepsilon_iεi越小越好。
2. 模型求解
由于假设模型的误差项是服从独立同分布(独立:数据之间互相不影响,同分布:保证模型使用于某一类数据)的高斯分布(标准正态分布)1,即ϵ∼N(0,σ2)\epsilon \sim N(0, \sigma^2)ϵ∼N(0,σ2),则其概率密度函数为
p(ϵi)=12πσexp(−εi22σ2)(2)p(\epsilon_i)=\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{\varepsilon_i^2}{2\sigma^2})(2)p(ϵi)=2πσ1exp(−2σ2εi2)(2)
对(1)式进行变形,则有εi=yi−θTxi\varepsilon_i=y_i-\theta^{^T} x_iεi=yi−θTxi,将其带入(2)式,得
p(yi∣xi,θ)=12πσexp(−(yi−θTxi)22σ2)p(y_i|x_i,\theta)=\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\theta^{^T} x_i)^2}{2\sigma^2})p(yi∣xi,θ)=2πσ1exp(−2σ2(yi−θTxi)2)
因为我们的目的是让求解得出的参数θ\thetaθ和和xix_ixi组合后,得到的估计值y^i=θTxi\hat{y}_i=\theta^{^T} x_iy^i=θTxi是真实值yiy_iyi的概率越大越好,也就是让这个概率越大越好。
由于以上只是单个的样本数据,假设我们有mmm个样本数据,样本之间互相独立,则所有的样本的概率等于单个样本的概率的乘积,我们将所有样本的概率记为似然函数L(θ)L(\theta)L(θ),则
L(θ)=∏i=0m12πσexp(−(yi−θTxi)22σ2)L(\theta)=\prod \limits_{i=0}^m\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\theta^{^T} x_i)^2}{2\sigma^2})L(θ)=i=0∏m2πσ1exp(−2σ2(yi−θTxi)2)
由于多个式子相乘难以求解,我们可利用对数将其转化为加法。两边同时取对数,得到对数似然函数lnL(θ)lnL(\theta)lnL(θ),
lnL(θ)=ln∏i=0m12πσexp(−(yi−θTxi)22σ2)lnL(\theta)=ln\prod \limits_{i=0}^m\frac{1}{\sqrt{2\pi}\sigma }exp(-\frac{(y_i-\theta^{^T} x_i)^2}{2\sigma^2})lnL(θ)=lni=0∏m2πσ1exp(−2σ2(yi−θTxi)2)
即
lnL(θ)=mln12πσ−1σ212∑i=1m(yi−θTxi)2lnL(\theta)=mln\frac{1}{\sqrt{2\pi}\sigma }-\frac{1}{\sigma^2}\frac{1}{2}\sum_{i=1}^m(y_i-\theta^{^T} x_i)^2lnL(θ)=mln2πσ1−σ2121i=1∑m(yi−θTxi)2
要对上述式子求最大值,则相当于对12∑i=1m(yi−θTxi)2\frac{1}{2}\sum_{i=1}^m(y_i-\theta^{^T} x_i)^221∑i=1m(yi−θTxi)2求最小值,我们将其记为J(θ)J(\theta)J(θ),并取名为目标函数,则目标函数为
J(θ)=12∑i=1m(yi−θTxi)2J(\theta)=\frac{1}{2}\sum_{i=1}^m(y_i-\theta^{^T} x_i)^2J(θ)=21i=1∑m(yi−θTxi)2
那么,求解这个目标函数所使用的方法就是最小二乘法,最小二乘法的代数法解法就是对θi\theta_iθi求偏导数,令偏导数为0,再解方程组,得到θi\theta_iθi的估计值。矩阵法比代数法要简洁,下面主要讲解下矩阵法解法。
由于
J(θ)=12∑i=1m(yi−θTxi)2=12∑i=1m(θTxi−yi)2=12(Xθ−Y)T(Xθ−Y)J(\theta)=\frac{1}{2}\sum_{i=1}^m(y_i-\theta^{^T} x_i)^2=\frac{1}{2}\sum_{i=1}^m(\theta^{^T} x_i-y_i)^2=\frac{1}{2}(X\theta-Y)^{^T}(X\theta-Y)J(θ)=21i=1∑m(yi−θTxi)2=21i=1∑m(θTxi−yi)2=21(Xθ−Y)T(Xθ−Y)
我们需要对其求偏导,∂J(θ)∂θ=12∂(θTXTXθ−θTXTY−YTXθ+YTY)∂θ=12(2XTXθ−2XTY)\frac{\partial J(\theta)}{\partial \theta}=\frac{1}{2}\frac{\partial (\theta^{^T}X^{^T}X\theta-\theta^{^T}X^{^T}Y-Y^{^T}X\theta+Y^{^T}Y)}{\partial \theta}=\frac{1}{2}(2X^{^T}X\theta-2X^{^T}Y)∂θ∂J(θ)=21∂θ∂(θTXTXθ−θTXTY−YTXθ+YTY)=21(2XTXθ−2XTY),令其等于0,得θ^=(XTX)−1XTY\hat \theta=( X^{^T}X)^{-1}X^{^T}Yθ^=(XTX)−1XTY
这里,需要用到矩阵求导的公式2.
在了解正态分布之前,我们需要先了解一个概念——概率分布。概率分布是指:经过大量的重复试验,将随机事件的所有可能的出现结果的次数分布记录下来,并在坐标系中做出一条曲线,这条曲线就是数据的概率分布曲线,由概率分布曲线可以估算变量的概率。正态分布就是一种常见的概率分布,它的概率分布曲线是一个钟形曲线,生活中大量的变量都服从正态分布,例如:人群的身高、鞋码、学生成绩等。正态分布只依赖于数据的两个特征:均值和方差。标准正态分布的均值为0,方差为σ2\sigma^2σ2. ↩︎
∂XTA∂A=∂ATX∂X=A,∂XTAX∂X=AX+ATX\frac{\partial X^{^T} A }{\partial A}=\frac{\partial A^{^T} X }{\partial X}=A, \frac{\partial X^{^T} A X}{\partial X}=AX+ A^{^T} X∂A∂XTA=∂X∂ATX=A,∂X∂XTAX=AX+ATX ↩︎
相关文章:

第1节 线性回归模型
1. 模型概述 对于收集到的数据(xi,yi)(x_i,y_i)(xi,yi),建立线性回归模型yiθTxiεi(1)y_i\theta^{^T} x_i \varepsilon_i (1)yiθTxiεi(1) 需要估计的参数为θT\theta^{^T}θT,我们的目的是让估计的参数θT\theta^{^T}θT和xix_ixi…...
CodeGeeX 130亿参数大模型的调优笔记:比FasterTransformer更快的解决方案
0x0 背景 相信大家都使用或者听说过github copilot这个高效的代码生成工具。CodeGeeX类似于github copilot,是由清华大学,北京智源研究院,智谱AI等机构共同开发的一个拥有130亿参数的多编程语言代码生成预训练模型。它在vscode上也提供了插件…...

Linux驱动之并发与竞争
文章目录并发与竞争的概念原子操作原子整形操作 API 函数原子位操作 API 函数自旋锁自旋锁简介自旋锁结构体自旋锁 API 函数自旋锁的注意事项读写自旋锁读写自旋锁的API顺序锁顺序锁的APIRCU(Read-Copy-Update)RCU的API信号量信号量API互斥体互斥体的API完成量(Completion)完成…...

【密码学复习】第四讲分组密码(三)
AES算法的整体结构 AES算法的轮函数 1)字节代换(SubByte) 2)行移位(ShiftRow) 3)列混合(MixColumn) 4)密钥加(AddRoundKey)1-字节代换…...

JVM(内存划分,类加载,垃圾回收)
JVMJava程序,是一个名字为Java 的进程,这个进程就是所说的“JVM”1.内存区域划分JVM会先从操作系统这里申请一块内存空间,在这个基础上再把这个内存空间划分为几个小的区域在一个JVM进程中,堆和方法区只有一份;栈和程序…...

工作中遇到的问题 -- 你见过哪些写的特别好的代码
strPtr : uintptr((*(*stringStruct)(unsafe.Pointer(&str))).str)代码解析: 这是一段 Go 代码,它的作用是获取一个字符串变量 str 的底层指针,即字符串数据的起始地址。 这段代码涉及到了 Go 语言中的指针、类型转换和内存布局等概念&…...

基于chatGPT设计卷积神经网络
1. 简介 本文主要介绍基于chatGPT,设计一个针对骁龙855芯片设计的友好型神经网络。 提问->跑通总共花了5min左右,最终得到的网络在Cifar100数据集上与ResNet18的精度对比如下。 模型flopsparamstrain acc1/5test acc1/5ResNet18(timm)1.8211.18~98…...

java.sql.Date和java.util.Date的区别
参考答案 java.sql.Date 是 java.util.Date 的子类java.util.Date 是 JDK 中的日期类,精确到时、分、秒、毫秒java.sql.Date 与数据库 Date 相对应的一个类型,只有日期部分,时分秒都会设置为 0,如:2019-10-23 00:00:0…...
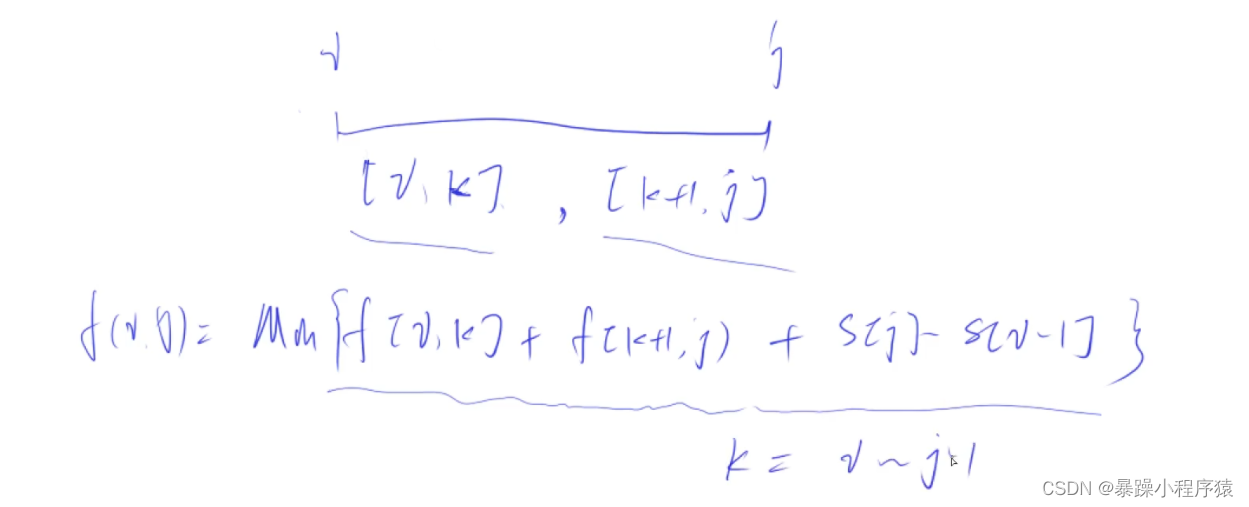
动态规划---线性dp和区间dp
动态规划(三) 目录动态规划(三)一:线性DP1.数字三角形1.1数字三角形题目1.2代码思路1.3代码实现(正序and倒序)2.最长上升子序列2.1最长上升子序列题目2.2代码思路2.3代码实现3.最长公共子序列3.1最长公共子序列题目3.2代码思路3.3代码实现4.石子合并4.1题目如下4.2代…...

常见的2D与3D碰撞检测算法
分离轴分离轴定理(Separating Axis Theorem)是用于解决2D或3D物体碰撞检测问题的一种方法。其基本思想是,如果两个物体未发生碰撞,那么可以找到一条分离轴(即一条直线或平面),两个物体在该轴上的…...

STM32 10个工程篇:1.IAP远程升级(二)
一直提醒自己要更新CSDN博客,但是确实这段时间到了一个项目的关键节点,杂七杂八的事情突然就一涌而至。STM32、FPGA下位机代码和对应Labview的IAP升级助手、波形设置助手上位机代码笔者已经调试通过,因为不想去水博客、凑数量,复制…...
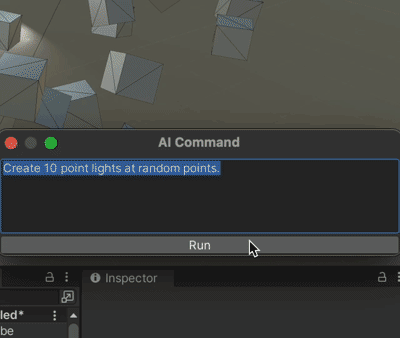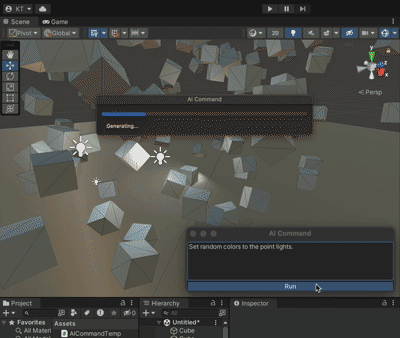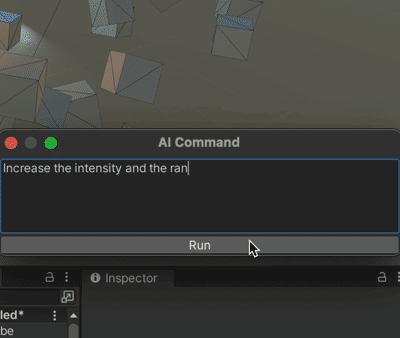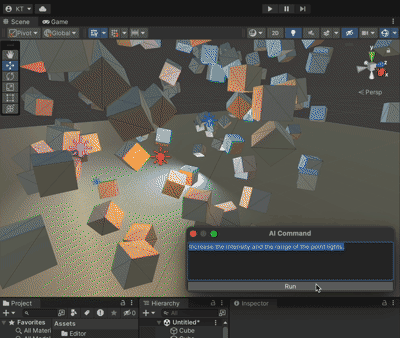
Unity+ChatGpt的联动 AICommand
果然爱是会消失的,对吗 chatGpt没出现之前起码还看人家的文章,现在都是随便你。 本着师夷长技以制夷的思路,既然打不过,那么我就加入 github地址:https://github.com/keijiro/AICommand 文档用chatGpt翻译如下&#…...
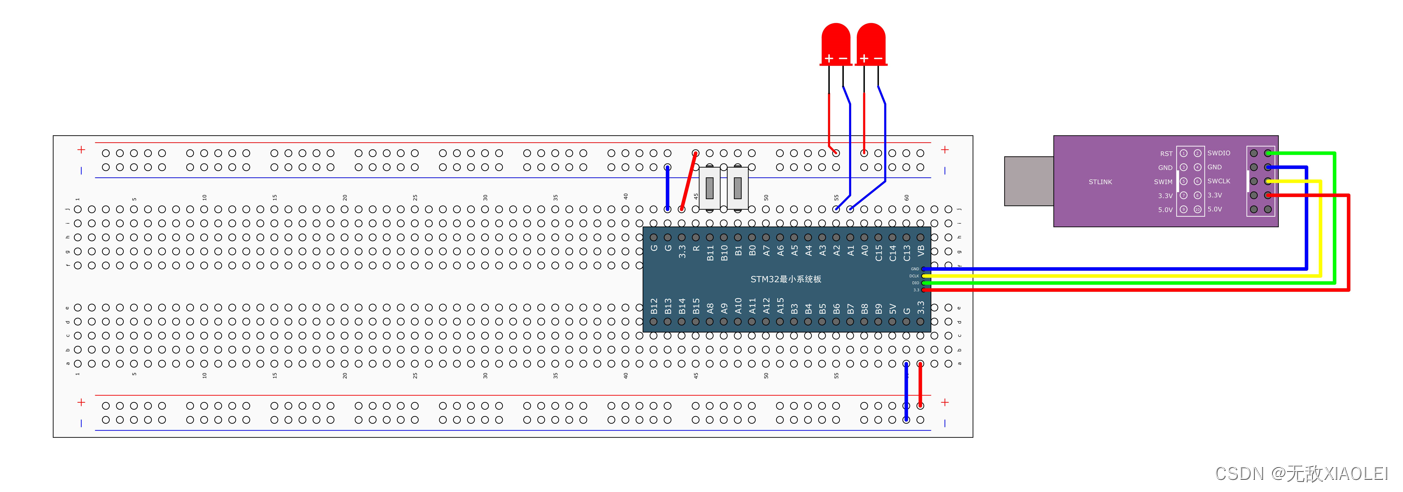
STM-32:按键控制LED灯 程序详解
目录一、基本原理二、接线图三、程序思路3.1库函数3.2程序代码注:一、基本原理 左边是STM322里电路每一个端口均可以配置的电路部分,右边部分是外接设备 电路图。 配置为 上拉输入模式的意思就是,VDD开关闭合,VSS开关断开。 浮空…...
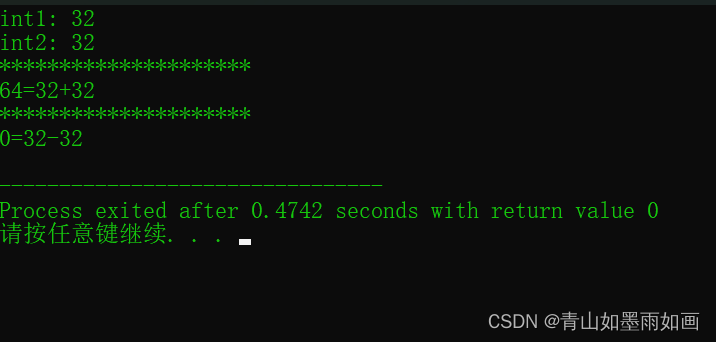
北邮22信通:(8)实验1 题目五:大整数加减法(搬运官方代码)
北邮22信通一枚~ 跟随课程进度每周更新数据结构与算法的代码和文章 持续关注作者 解锁更多邮苑信通专属代码~ 上一篇文章: 北邮22信通:(7)实验1 题目四:一元多项式(节省内存版)_青山如…...

Fiddler抓取https史上最强教程
有任何疑问建议观看下面视频 2023最新Fiddler抓包工具实战,2小时精通十年技术!!!对于想抓取HTTPS的测试初学者来说,常用的工具就是fiddler。 但是初学时,大家对于fiddler如何抓取HTTPS难免走歪路ÿ…...
STM32开发基础知识入门
C语言基础 位操作 对基本类型变量可以在位级别进行操作。 1) 不改变其他位的值的状况下,对某几个位进行设值。 先对需要设置的位用&操作符进行清零操作,然后用|操作符设值。 2) 移位操作提高代码的可读性。 3) ~取反操作使用技巧 可用于对某…...

学习操作系统的必备教科书《操作系统:原理与实现》| 文末赠书4本
使用了6年的实时操作系统,是时候梳理一下它的知识点了 摘要: 本文简单介绍了博主学习操作系统的心路历程,同时还给大家总结了一下当下流行的几种实时操作系统,以及在工程中OSAL应该如何设计。希望对大家有所启发和帮助。 文章目录…...
)
大数据的常用算法(分类、回归分析、聚类、关联规则、神经网络方法、web数据挖掘)
在大数据时代,数据挖掘是最关键的工作。大数据的挖掘是从海量、不完全的、有噪声的、模糊的、随机的大型数据库中发现隐含在其中有价值的、潜在有用的信息和知识的过程,也是一种决策支持过程。其主要基于人工智能,机器学习,模式学…...
【数据结构】详解二叉树与堆与堆排序的关系
🌇个人主页:平凡的小苏 📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情 🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html 🚀数据结构专栏ÿ…...
【Pandas】数据分析入门
文章目录前言一、Pandas简介1.1 什么是Pandas1.2 Pandas应用二、Series结构2.1 Series简介2.2 基本使用三、DataFrame结构3.1 DataFrame简介3.2 基本使用四、Pandas-CSV4.1 CSV简介4.2 读取CSV文件4.3 数据处理五、数据清洗5.1 数据清洗的方法5.2 清洗案例总结前言 大家好&…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
