Java算法之计数排序(Counting Sort)
简介
计数排序是一种线性时间复杂度的排序算法,它不依赖于元素之间的比较,而是通过统计数组中每个元素出现的次数,然后根据这些统计信息对元素进行排序。这种算法特别适用于整数且整数的范围不是非常大时。
算法步骤
- 找出数组中的最大值。
- 创建一个计数数组,长度为最大值加一。
- 遍历原数组,对每个元素在计数数组中对应的位置加一。
- 再次遍历计数数组,将每个非零元素按顺序累加到原数组。
//countingSort 方法接受数组和最大值作为参数,执行计数排序。
//首先创建一个计数数组,长度为最大值加一。
//遍历原数组,统计每个元素出现的次数。
//再次遍历计数数组,将非零元素累加到原数组。
//main 方法中,我们初始化一个数组,找出最大值,然后调用 countingSort 方法进行排序,并打印排序后的结果。
public class CountingSort {// 计数排序方法public static void countingSort(int[] arr, int maxVal) {int n = arr.length;int[] count = new int[maxVal + 1]; // 创建计数数组// 统计每个元素出现的次数for (int i = 0; i < n; i++) {count[arr[i]]++;}// 将计数数组中非零元素累加到原数组int index = 0;for (int i = 0; i < count.length; i++) {while (count[i] > 0) {arr[index++] = i;count[i]--;}}}public static void main(String[] args) {int[] arr = {4, 2, 2, 8, 3, 3, 1};int maxVal = getMaxVal(arr); // 找出数组中的最大值countingSort(arr, maxVal);// 打印排序后的数组for (int i = 0; i < arr.length; i++) {System.out.print(arr[i] + " ");}}// 辅助方法,找出数组中的最大值private static int getMaxVal(int[] arr) {int max = arr[0];for (int i = 1; i < arr.length; i++) {if (arr[i] > max) {max = arr[i];}}return max;}
}优点
- 时间效率:对于小范围整数排序,计数排序的时间复杂度是O(n+k),其中n是数组长度,k是整数的范围。
- 稳定性:计数排序是稳定的排序算法,相等元素的相对位置不会改变。
- 简单性:算法逻辑简单,容易实现。
缺点
- 空间复杂度:计数排序需要额外的存储空间,其大小取决于整数的范围,空间复杂度为O(k)。
- 适用范围:只适用于整数排序,对于非整数或整数范围非常大的情况,效率不高。
时间复杂度和空间复杂度分析
- 时间复杂度:O(n+k),其中n是数组长度,k是整数的范围。
- 空间复杂度:O(k),需要一个大小为k的计数数组。
使用场景
- 当整数的范围k远小于数组长度n时,计数排序非常高效。
- 适用于对固定范围的整数进行排序,如统计字符出现次数。
相关文章:
)
Java算法之计数排序(Counting Sort)
简介 计数排序是一种线性时间复杂度的排序算法,它不依赖于元素之间的比较,而是通过统计数组中每个元素出现的次数,然后根据这些统计信息对元素进行排序。这种算法特别适用于整数且整数的范围不是非常大时。 算法步骤 找出数组中的最大值。…...

【系统架构设计师-2012年】综合知识-答案及详解
更多内容请见: 备考系统架构设计师-核心总结索引 文章目录 【第1~2题】【第3~4题】【第5题】【第6题】【第7题】【第8题】【第9题】【第10~11题】【第12~13题】【第14~19题】【第20~21题】【第22~24题】【第25~26题】【第27~31题】【第32~33题】【第34~36题】【第37…...

webpack4手动搭建Vue项目
小满视频 很多解释使用通义灵码搜的,通义灵码的搜索结果也是有错误的全程使用pnpm包管理工具,和npm的用法基本一样 学习总结 1. 多看看webpack官网 2. webpack的作用:配置一堆东西,达到运行程序的目的 3. 无论什么东西都转成js,…...
)
Python爬虫所需的技术及其原理(简单易懂)
导言 随着互联网的发展,大量的数据被存储在网络上,而我们需要从中获取有用的信息。Python作为一种功能强大且易于学习的编程语言,被广泛用于网络爬虫的开发。本文将详细介绍Python爬虫所需的技术及其原理,并提供相关的代码案例。…...

FxFactory 8 for Mac 视觉特效插件包安装
Mac分享吧 文章目录 介绍页面效果一、下载软件二、开始安装1、Install安装2、显示软件页面,表示安装成功3、补丁安装 三、注意事项1、若已安装过其他版本,需要使用软件自带的卸载功能进行软件卸载,再安装此版本 安装完成!&#x…...

将语义分割的标签转换为实例分割(yolo)的标签
语义分割的标签(目标处为255,其余处为0) 实例分割的标签(yolo.txt),描述边界的多边形顶点的归一化位置 绘制在原图类似蓝色的边框所示。 废话不多说,直接贴代码; import os import cv2 imp…...

QT 遍历ini配置文件
在 Qt 中,处理 INI 配置文件是一项常见任务,通常使用 QSettings 类来读取和写入这些文件。QSettings 提供了一种方便的方式来操作 INI 文件中的配置数据。下面是如何使用 QSettings 遍历和处理 INI 配置文件的示例。 示例代码 假设有一个名为 config.i…...

ecmascript和javascript的区别详细讲解
大家好,我是程序员小羊! 前言: ECMAScript 和 JavaScript是紧密相关的术语,但它们有着各自明确的定义和用途。要理解它们的区别,首先需要从它们的起源、发展历史、技术架构以及具体应用领域来分析。以下是对它们的详…...

【Python报错已解决】“ModuleNotFoundError: No module named ‘timm‘”
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《C干货基地》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! 文章目录 引言:一、问题描述1.1 报错示例:当我们尝试导入timm库时,可能会看到以下错误信息。…...
)
「图::存储」链式邻接表|链式前向星(C++)
前置知识 上一节我们介绍了三种基本的存图结构: 「图」邻接矩阵|边集数组|邻接表(C) 概述 他们各有优劣,为了综合他们的性能, 这一节我们来介绍两种以这三种结构为基础实现的高级存储结构:链式邻接表|…...
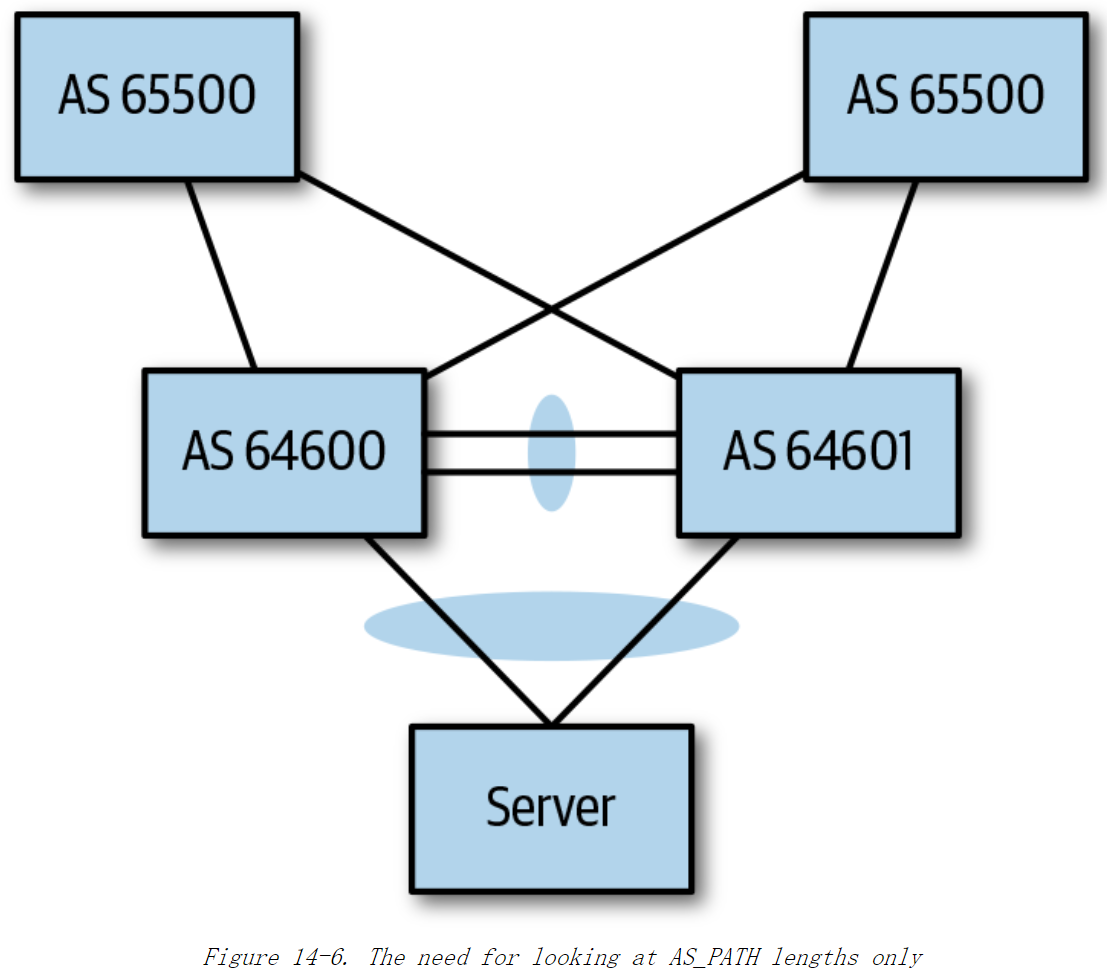
《Cloud Native Data Center Networking》(云原生数据中心网络设计)读书笔记 -- 10数据中心中的BGP
本章解答以下问题: ASN,团体(community),属性(attribute),最佳路径这些BGP术语是什么疑似?在数据中心中应该使用eBGP还是iBGP?在数据中心使用BGP时,应采用什…...

unity游戏开发——标记物体 一目了然
Unity游戏开发:标记物体,让开发变得一目了然 “好读书,不求甚解;每有会意,便欣然忘食。” 本文目录: Unity游戏开发 Unity游戏开发:标记物体,让开发变得一目了然前言1. 什么是Tag?2. Unity中如何添加和管理Tag步骤1&am…...

vue 项目打包图片没有打包进去问题解决
解决方法1.在导入图片的文件中通过 import 引入图片 这种方法只适合图片少的情况 <template> <img :srctestImg/> </template> <script> import testImg from /assets/img/testImg.png </script>2.封装公共方法,通过 new URL() 的方式…...

TCP的传输速度
如何确定TCP最大传输速度? TCP 的传输速度,受限于发送窗⼝,接收窗⼝以及⽹络设备传输能⼒。 其中,窗⼝⼤⼩由内核缓冲区⼤⼩决定。如果缓冲区与⽹络传输能⼒匹配,那么缓冲区的利⽤率就达到了最⼤化。 如何计算网络传…...
直播间的“骆驼”比沙漠还多?刀郎演唱会惊现“骆驼”
“送战友,踏征程,默默无语两行泪,耳边响起驼铃声……”8月30日,刀郎知交线上演唱会在微信视频号直播。一曲《驼铃》,勾起了无数人的回忆,离别的伤感、人性的关怀与温暖,通过悠然的旋律流入千万听…...

Android Studio gradle下载太慢了!怎么办?(已解决)
Android Studio!你到底干了什么?! 不能高速下载gradle,我等如何进行app编程?! 很简单,我修改gradle地址不就是了。 找到gradle-wrapper.properties文件 修改其中distributionUrl的地址。 将 ht…...
安卓版Infuse来了 打造自己的影视墙
如何让安卓设备上的视频播放更高效?AfuseKt 或许能给出答案 AfuseKt 是一款功能强大的安卓网络视频播放器,专为满足用户对多样化媒体播放需求而设计。它不仅支持多种流行的在线存储和媒体管理平台,如阿里云盘、Alist、WebDAV 和 Emby 等&…...
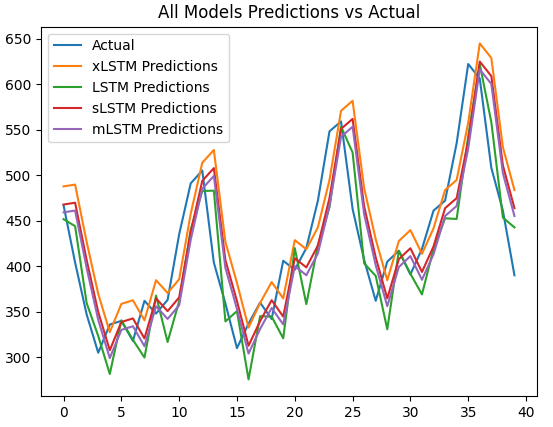
【Python时序预测系列】高创新模型:基于xlstm模型实现单变量时间序列预测(案例+源码)
这是我的第351篇原创文章。 一、引言 LSTM在1990年代被提出,用以解决循环神经网络(RNN)的梯度消失问题。LSTM在多种领域取得了成功,但随着Transformer技术的出现,其地位受到了挑战。如果将LSTM扩展到数十亿参数&#…...

Ubuntu 22.04 系统中 ROS2安装
Ubuntu 22.04 系统中 ROS2安装 ROS2安装 # 多窗口终端工具 sudo apt update sudo apt install tilix打开软件,点击右上角图标进入设置 -> General -> size120, columns:48Command -> 勾选第一个 Run command as login shellColor -> Theme Color 选择…...

Vue内置指令v-once、v-memo和v-pre提升性能?
前言 Vue的内置指令估计大家都用过不少,例如v-for、v-if之类的就是最常用的内置指令,但今天给大家介绍几个平时用的比较少的内置指令。毕竟这几个Vue内置指令可用可不用,不用的时候系统正常跑,但在对的地方用了却能提升系统性能&…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
