Leetcode3259. 超级饮料的最大强化能量
Every day a Leetcode
题目来源:3259. 超级饮料的最大强化能量
解法1:记忆化搜索
本题的状态定义 dfs(i,j)。其中 j=0,1,分别表示最后选的是 energyDrinkA[i] 还是 energyDrinkB[i]。
为方便实现,把 energyDrinkA 和 energyDrinkB 加到一个长为 2 的二维数组 c 中。
分类讨论:
-
继续选 c[j] 中的元素,那么下一个数选 c[j][i−1],需要解决的问题为:从下标 [0,i−1] 中选数字,且最后选的是 c[j] 中的元素的情况下,所选元素之和的最大值,即 dfs(i−1,j)。
-
改成选 c[j⊕1] 中的元素,那么下一个数选 c[j⊕1][i−2],需要解决的问题为:从下标 [0,i−2] 中选数字,且最后选的是 c[j⊕1] 中的元素的情况下,所选元素之和的最大值,即 dfs(i−2,j⊕1)。其中 ⊕ 为异或运算,通过异或 1,可以把 0 变成 1,把 1 变成 0。
代码:
#
# @lc app=leetcode.cn id=3259 lang=python3
#
# [3259] 超级饮料的最大强化能量
## @lc code=start
class Solution:def maxEnergyBoost(self, energyDrinkA: List[int], energyDrinkB: List[int]) -> int:n = len(energyDrinkA)energyDrink = (energyDrinkA, energyDrinkB)@cache # 缓存装饰器,避免重复计算 dfs 的结果(记忆化)def dfs(i: int, j: int) -> int:if i < 0:return 0res1 = dfs(i - 1, j) + energyDrink[j][i]res2 = dfs(i - 2, j ^ 1) + energyDrink[j][i]return max(res1, res2)return max(dfs(n - 1, 0), dfs(n - 1, 1))
# @lc code=end
结果:

复杂度分析:
时间复杂度:O(n),其中 n 为数组 energyDrinkA/energyDrinkB 的长度。由于每个状态只会计算一次,动态规划的时间复杂度 = 状态个数 × 单个状态的计算时间。本题状态个数等于 O(n),单个状态的计算时间为 O(1),所以总的时间复杂度为 O(n)。
空间复杂度:O(n),其中 n 为数组 energyDrinkA/energyDrinkB 的长度。保存多少状态,就需要多少空间。
解法2:动态规划
代码:
/** @lc app=leetcode.cn id=3259 lang=cpp** [3259] 超级饮料的最大强化能量*/// @lc code=start
class Solution
{
public:long long maxEnergyBoost(vector<int> &energyDrinkA, vector<int> &energyDrinkB){int n = energyDrinkA.size();vector<array<long long, 2>> dp(n + 2);// 状态转移for (int i = 0; i < n; i++){dp[i + 2][0] = max(dp[i + 1][0], dp[i][1]) + energyDrinkA[i];dp[i + 2][1] = max(dp[i + 1][1], dp[i][0]) + energyDrinkB[i];}return max(dp[n + 1][0], dp[n + 1][1]);}
};
// @lc code=end
结果:

复杂度分析:
时间复杂度:O(n),其中 n 为数组 energyDrinkA/energyDrinkB 的长度。
空间复杂度:O(n),其中 n 为数组 energyDrinkA/energyDrinkB 的长度。
相关文章:

Leetcode3259. 超级饮料的最大强化能量
Every day a Leetcode 题目来源:3259. 超级饮料的最大强化能量 解法1:记忆化搜索 本题的状态定义 dfs(i,j)。其中 j0,1,分别表示最后选的是 energyDrinkA[i] 还是 energyDrinkB[i]。 为方便实现,把 energyDrinkA 和 energyDri…...

Java题集(由入门到精通)03
此系列文章收录大量Java经典代码题(也可以算是leetcode刷题指南),希望可以与大家一起努力学好Java。3、2、1,请看! 目录 1.创建学生成绩表 2.冒泡排序 3.模拟彩票中奖 4.杨辉三角 1.创建学生成绩表 输入n个学生的…...
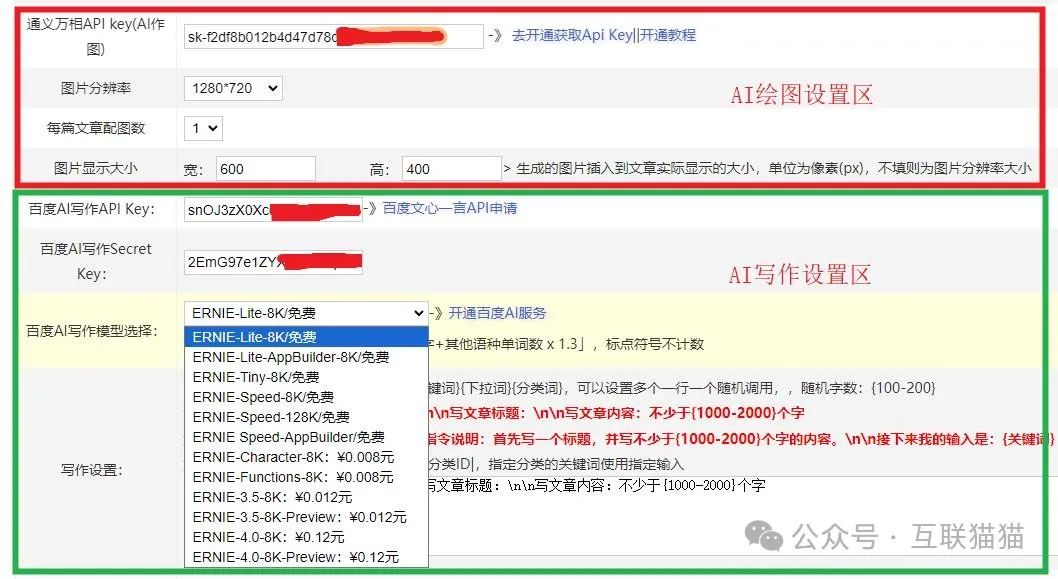
zblog自动生成文章插件(百度AI写作配图,图文并茂)
最近工作比较忙,导致自己的几个网站都无法手动更新,于是乎也想偷个懒把,让AI帮忙打理下自己的网站。我接触chatgpt等AI工具还是比较早了,从openai推出gpt3.5就一直在用,说实话,开始的时候用AI自动更新网站还…...

华为 HCIP-Datacom H12-821 题库 (4)
有需要题库的可以看主页置顶 V群仅进行学习交流 1.缺省情况下,广播型网络中运行 IS-IS 的路由器,DIS 发送 CSNP报文的周期为多少秒? A、10 B、3.3 C、30 D、40 答案:A 解析: 广播型网络中运行 IS-IS 的路由器&am…...

使用seq_file
在《使用procfs》一文的源码示例中有说到proc文件系统每次读取的数据只能是1个页,如果超过则需多次读取,这样的话会增加读取次数,增多系统调用次数,影响了整体的效率,故而才有seq file序列文件的出现,该项功能使得内核对于大文件的读取更加容易。 对于seq file,其结构…...
-ES 和 (μ+λ)-ES)
期货赫兹量化-种群优化算法:进化策略,(μ,λ)-ES 和 (μ+λ)-ES
进化策略(Evolution Strategies, ES)是一种启发式算法,旨在模仿自然选择的过程来解决复杂的优化问题,尤其在没有显式解、或搜索空间巨大的情况下表现良好。基于自然界的进化原理,进化策略通过突变、选择等遗传算子迭代…...

pytest实战演练
pytest实战演练 pycharm常见操作 创建项目使用虚拟环境 创建文件夹的时候建议使用的创建方式 这样创建是因为python3.0版本之后导包无区别,之前版本导包会报错的 _init_.py文件中建议为空不写内容 _all_[]的含义 是将列表中的方法或变量或类暴漏出去便于使用的生效…...

7、关于LoFTR
7、关于LoFTR LoFTR论文链接:LoFTR LoFTR的提出,是将Transformer模型的注意力机制在特征匹配方向的应用,Transformer的提取特征的机制,在自身进行,本文提出可以的两张图像之间进行特征计算,非常适合进行特…...

硬件工程师笔试面试知识器件篇——电感
目录 3、电感 3.1、基础 电感原理图 电感实物图 3.1.1、定义与单位 1)定义: 2) 单位: 3.1.2、物理原理 1)法拉第电磁感应定律: 2)楞次定律: 3.1.3、电感器的构造 3.1.4、类型 3.1.5、应用 3.1.6、特性 3.1.7、设计考虑 3.2、相关问题 3.…...

代码随想录八股训练营第三十六天| C++
前言 一、push_back()和emplace_back()的区别? 1.1.push_back(): 1.2.emplace_back(): 1.3.区别总结: 1.4.使用场景: 二、map dequeu list 的实现原理? 2.1.std::map: 2.2. std::deque: 2.3. std::list: 2.4. 区别总结: 总结 前言…...

学习计算机网络
a类0~127,b类128~191,c类192~223 网络地址:看子网掩码,分网络位和主机位,后面是主机位,主机位全部为0,网络地址。 直接广播地址:看子网掩码,分网络位和主机位ÿ…...

Django发送邮件
【图书介绍】《Django 5企业级Web应用开发实战(视频教学版)》_django 5企业级web应用开发实战(视频教学版)-CSDN博客 Django 5框架Web应用开发_夏天又到了的博客-CSDN博客 本文学习怎么使用Django发送邮件。 尽管使用Python的smtplib模块发送电子邮件…...

T7:咖啡豆识别
T7:咖啡豆识别 **一、前期工作**1.设置GPU,导入库2.导入数据3.查看数据 **二、数据预处理**1.加载数据2.可视化数据3.配置数据集 **三、构建CNN网络模型**1、手动搭建2、直接调用官方模型 **四、编译模型****五、训练模型****六、模型评估****七、预测**八、暂时总结…...

【MATLAB】FIR滤波器的MATLAB实现
FIR滤波器的MATLAB实现 FIR滤波器的设计fir1函数fir2函数 与IIR滤波器相比,FIR滤波器既有其优势也有其局限性。FIR滤波器的主要优点包括: 精确的线性相位响应;永远保持稳定性;设计方法通常是线性的;在硬件实现中具有更…...

【RabbitMQ之一:windows环境下安装RabbitMQ】
目录 一、下载并安装Erlang1、下载Erlang2、安装Erlang3、配置环境变量4、验证erlang是否安装成功 二、下载并安装RabbitMQ1、下载RabbitMQ2、安装RabbitMQ3、配置环境变量4、验证RabbitMQ是否安装成功5、启动RabbitMQ服务(安装后服务默认自启动) 三、安…...

ISO26262和Aspice之间的关联
ASPICE 介绍: ASPICE(Automotive Software Process Improvement and Capability dEtermination)是汽车软件过程改进及能力评定的模型,它侧重于汽车软件的开发过程。ASPICE 定义了一系列的过程和活动,包括需求管理、软…...

对极约束及其性质 —— 公式详细推导
Title: 对极约束及其性质 —— 公式详细推导 文章目录 前言1. 对极约束 (Epipolar Constraint)2. 坐标转换 (Coordinate Transformations)3. 像素坐标 (Pixel Coordinates)4. 像素坐标转换 (Transformations of Pixel Coordinates)5. 本质矩阵 (Essential Matrix)6. 线坐标 (Co…...

【论文精读】SCINet-基于降采样和交互学习的时序卷积模型
《SCINet: Time Series Modeling and Forecasting with Sample Convolution and Interaction》的作者团队来自香港中文大学,发表在NeurIPS 2022会议上。 动机 该论文的出发点是观察到时间序列数据具有独特的属性:即使在将时间序列下采样成两个子序列后,时间关系(例如数据…...
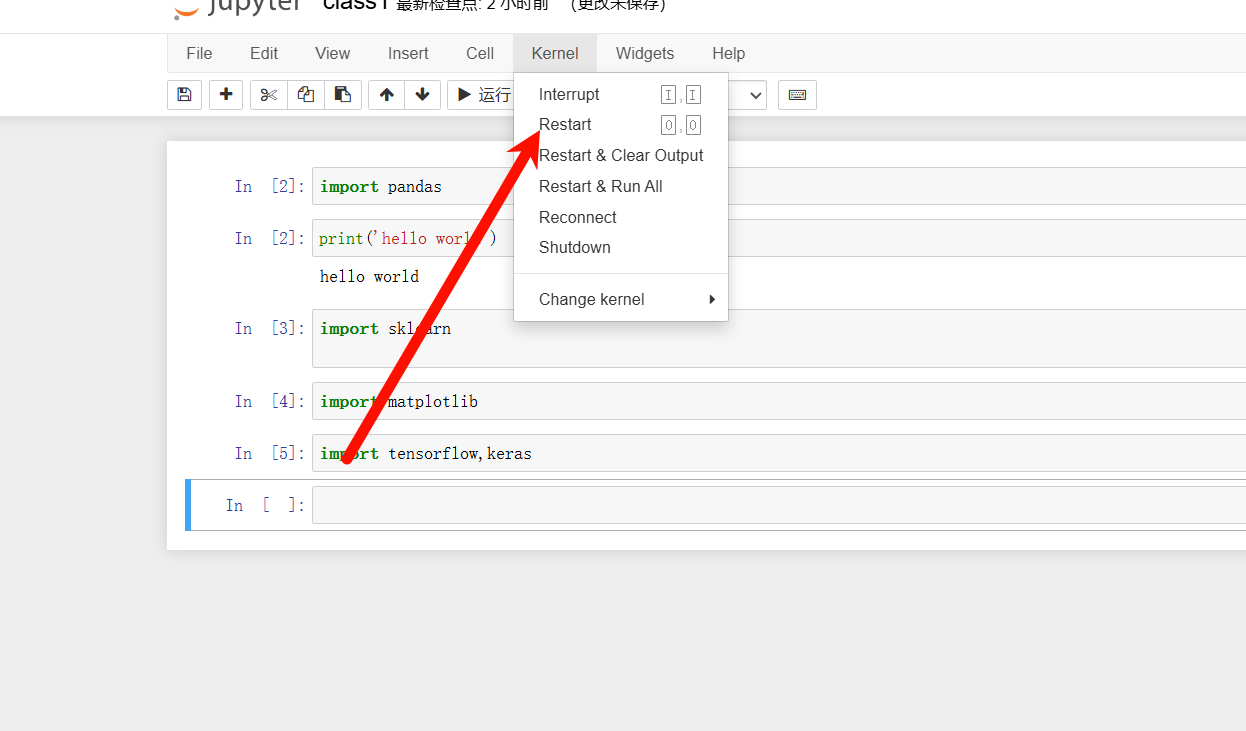
深度学习与大模型第1课环境搭建
文章目录 深度学习与大模型第1课环境搭建1. 安装 Anaconda2. 修改环境变量2.1 修改 .condarc 文件2.2 使用 Anaconda Prompt 修改环境变量 3. 新建 .ipynb 文件 机器学习基础编程:常见问题: 深度学习与大模型第1课 环境搭建 1. 安装 Anaconda 首先&am…...

JDK新特性
LTS Record jdk16 不是方法 是一个定 # Sealed Class/Interface jdk17 限制只能由某些类继承 CompletableFuture jkd8 PatternMatching of instanceOf jdk16 switch expressions jdk14 Stream.collect() Collector Collector API Collector.groupBy Collector实战 1. …...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
