【数据结构】你真的学会了二叉树了吗,来做一做二叉树的算法题及选择题

文章目录
- 1. 二叉树算法题
- 1.1 单值二叉树
- 1.2 相同的树
- 1.3 另一棵树的子树
- 1.4 二叉树的遍历
- 1.5 二叉树的构建及遍历
- 2. 二叉树选择题
- 3. 结语
1. 二叉树算法题
1.1 单值二叉树
https://leetcode.cn/problems/univalued-binary-tree/description/
1.2 相同的树
https://leetcode.cn/problems/same-tree/description/
基于上一道OJ题,拓展学习
对称二叉树:https://leetcode.cn/problems/symmetric-tree/description/
1.3 另一棵树的子树
https://leetcode.cn/problems/subtree-of-another-tree/description/
1.4 二叉树的遍历
前序遍历:
https://leetcode.cn/problems/binary-tree-preorder-traversal/description/
中序遍历:
https://leetcode.cn/problems/binary-tree-inorder-traversal/description/
后序遍历:
https://leetcode.cn/problems/binary-tree-postorder-traversal/description/
1.5 二叉树的构建及遍历
https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef
2. 二叉树选择题
💡 二叉树性质
对任何一棵二叉树, 如果度为 0 0 0其叶结点个数为 n 0 n_0 n0, 度为 2 2 2的分支结点个数为 n 2 n_2 n2 ,则有 n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1

证明上述性质:
假设一个二叉树有a个度为2的节点,b个度为1的节点,c个叶节点,则这个二叉树的边数是2a+b
另一方面,由于共有a+b+c个节点,所以边数等于a+b+c-1
结合上面两个公式:
2a+b = a+b+c-1 ,即:a = c-1
根据二叉树的性质,完成以下选择题:
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
3.一棵完全二叉树的结点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 124.一个具有767个结点的完全二叉树,其叶子结点个数为()
A 383
B 384
C 385
D 386
答案:
1.B
2.A
3.B
4.B
链式二叉树遍历选择题
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A E
B F
C G
D H
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为____。
A adbce
B decab
C debac
D abcde
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
答案:
1.A
2.A
3.D
4.A
3. 结语
今天的分享到这里就结束啦!如果觉得文章还不错的话,可以三连支持一下。
也可以点点关注,避免以后找不到我哦!
Crossoads主页还有很多有趣的文章,欢迎小伙伴们前去点评,您的支持就是作者前进的动力!

相关文章:

【数据结构】你真的学会了二叉树了吗,来做一做二叉树的算法题及选择题
文章目录 1. 二叉树算法题1.1 单值二叉树1.2 相同的树1.3 另一棵树的子树1.4 二叉树的遍历1.5 二叉树的构建及遍历 2. 二叉树选择题3. 结语 1. 二叉树算法题 1.1 单值二叉树 https://leetcode.cn/problems/univalued-binary-tree/description/ 1.2 相同的树 https://leetco…...

压力测试知识总结
压力测试知识总结 引言 随着信息技术的飞速发展,软件系统在各个行业中的应用越来越广泛,其稳定性和可靠性成为用户关注的焦点。压力测试作为软件测试中的一种重要方法,对于确保软件在高负载环境下的稳定性和可靠性具有重要意义。本文将从压…...

@import导入样式以及scss变量应用与static目录
import函数:使用import语句可以导入外联样式表,import后跟需要导入的外联样式表的相对路径,用;表示语句结束。 static目录:就是无论你有没有在这个目录里用过,它都会进行编译打包 import函数应用:先在在项目里创建一个common 目录, 目录里面分别创建css,…...
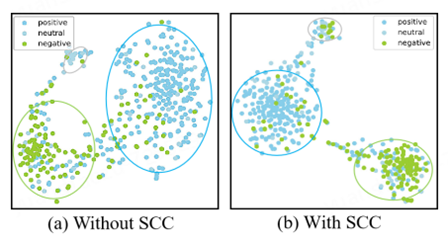
分类中的语义一致性约束:助力模型优化
前言 这里介绍一篇笔者在去年ACL上发表的一篇文章,使用了空间语义约束来提高多模态分类的效果,类似的思路笔者也在视频描述等方向进行了尝试,也都取得了不错的效果。这种建模时对特征进行有意义的划分和约束对模型还是很有帮助的,…...

前端框架介绍
前端框架是Web开发中不可或缺的工具,它们通过提供结构化的开发方式、模块化组件、响应式设计以及高效的性能优化,极大地简化了Web应用程序的开发过程。以下是对当前主流及新兴前端框架的详细介绍,这些框架不仅涵盖了广泛的功能,还…...

java基础知识-JVM知识详解
文章目录 一、JVM内存结构二、常见垃圾回收算法1. 标记-清除算法(Mark-Sweep Algorithm)2. 标记-整理算法(Mark-Compact Algorithm)3. 复制算法(Copying Algorithm)4. 分代收集算法(Generational Collection)5. 增量收集算法(Incremental Collection)6. 并行收集算法…...

流动会场:以声学专利为核心的完美移动场地—轻空间
流动会场作为一种全新的活动场所选择,凭借其便捷的移动性与先进的声学设计,正逐渐成为各类演出、会议和文化活动的热门场地。其独特之处不仅在于搭建速度快、灵活性高,还在于其核心技术——声学专利的强大支持。 专利声学设计,打造…...

深度学习(一)-感知机+神经网络+激活函数
深度学习概述 深度学习的特点 优点 性能更好 不需要特征工程 在大数据样本下有更好的性能 能解决某些传统机器学习无法解决的问题 缺点 小数据样本下性能不如机器学习 模型复杂 可解释性弱 深度学习与传统机器学习相同点 深度学习、机器学习是同一问题不同的解决方法 …...

目标检测-YOLOv4
YOLOv4介绍 YOLOv4 是 YOLO 系列的第四个版本,继承了 YOLOv3 的高效性,并通过大量优化和改进,在目标检测任务中实现了更高的精度和速度。相比 YOLOv3,YOLOv4 在框架设计、特征提取、训练策略等方面进行了全面升级。它在保持实时检…...

一台笔记本电脑的硬件都有哪些以及对应的功能
一台笔记本电脑的硬件通常包括多个关键组件,这些组件共同协作,确保电脑的正常运行。以下是笔记本电脑的主要硬件及其功能: 1. 中央处理器(CPU) 功能:CPU 是电脑的“大脑”,负责处理所有的计算…...

【程序分享1】第一性原理计算 + 数据处理程序
【1】第一性原理计算 数据处理程序 SMATool 程序:VASP QE 零温 有限温度 拉伸、剪切、双轴、维氏硬度的计算 ElasTool v3.0 程序:材料弹性和机械性能的高效计算和可视化工具包 VELAS 程序:用于弹性各向异性可视化和分析 Phasego 程序…...

【数据结构】栈与队列OJ题(用队列实现栈)(用栈实现队列)
目录 1.用队列实现栈oj题 对比 一、初始化 二、出栈 三、入栈 四、取队头元素: 2.用栈实现队列 一、定义 二、入队列 三、出队列 四、队头 五、判空 前言:如果想了解什么是栈和队列请参考上一篇文章进来一起把【数据结构】的【栈与队列】狠…...
element-ui打包之后图标不显示,woff、ttf加载404
1、bug 起因 昨天在 vue 项目中编写 element-ui 的树形结构的表格,发现项目中无法生效,定位问题之后发现项目使用的 element-ui 的版本是 2.4.11 。看了官方最新版本是 2.15.14,然后得知 2.4.11 版本是不支持表格树形结构的。于是决定升级 el…...

探究零工市场小程序如何改变传统兼职模式
近年来,零工市场小程序正逐渐改变传统的兼职模式,为求职者和雇主提供了一个更为高效、便捷的平台。本文将深入探讨零工市场小程序如何影响传统兼职模式,以及它带来的优势和挑战。 一、背景与挑战 传统的兼职市场往往存在信息不对称的问题&am…...
MySQL数据库安装(详细)—>Mariadb的安装(day21)
该网盘链接有效期为7天,有需要评论区扣我: 通过网盘分享的文件:mariadb-10.3.7-winx64.msi 链接: https://pan.baidu.com/s/1-r_w3NuP8amhIEedmTkWsQ?pwd2ua7 提取码: 2ua7 1 双击打开安装软件 本次安装的是mariaDB,双击打开mar…...
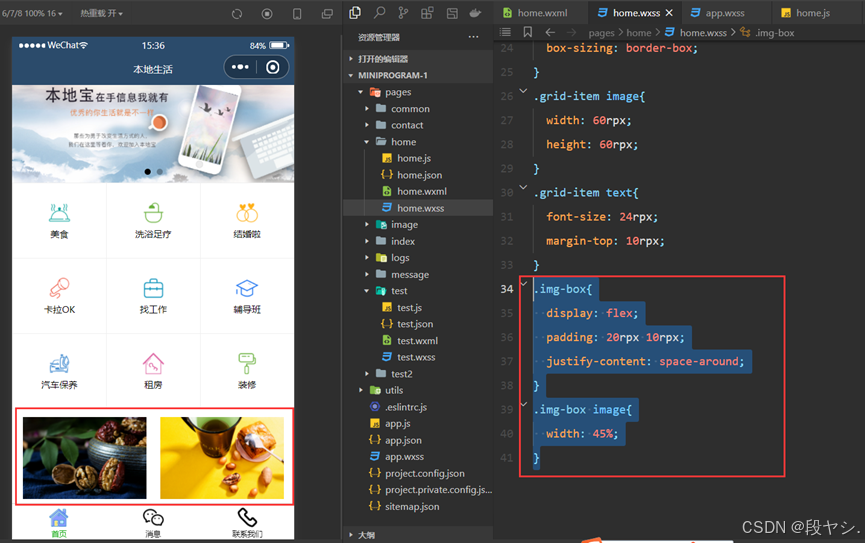
微信小程序实践案例
参考视频: https://www.bilibili.com/video/BV1834y1676P/?p36&spm_id_frompageDriver&vd_sourceb604c19516c17da30b6b1abb6c4e7ec0 前期准备 1、新建三个页面 "pages": ["pages/home/home","pages/message/message",&quo…...

DataLoader使用
文章目录 一、认识dataloader二、DataLoader整合数据集三、使用DataLoader展示图片方法四、去除结尾不满足batch_size设值图片的展示 一、认识dataloader DataLoader 用于封装数据集,并提供批量加载数据的迭代器。它支持自动打乱数据、多线程数据加载等功能。datas…...

CSS学习11--版心和布局流程以及几种分布的例子
版心和布局流程 一、版心二、布局流程三、一列固定宽度且居中四、两列左窄右宽五、通栏平均分布型 一、版心 版心:是指网页主题内容所在的区域。一般在浏览器窗口水平居中位置,常见的宽度值为960px、980px、1000px、1200px等。 二、布局流程 为了提高…...

NetSuite AI 图生代码
去年的ChatGPT热潮期间,我们写过一篇文章说GTP辅助编程的事。 NetSuite GPT的辅助编程实践_如何打开netsuite: html script notes的视图-CSDN博客文章浏览阅读2.2k次,点赞4次,收藏3次。作为GPT综合症的一种表现,我们今朝来探究下…...

Java - BigDecimal计算中位数
日常开发中,如果使用数据库来直接查询一组数据的中位数,就比较简单,直接使用对应的函数就可以了,例如: SUBSTRING_INDEX(SUBSTRING_INDEX(GROUP_CONCAT(目标列名 ORDER BY 目标列名),,,Count(1)/2),,,-1) AS 目标列名_…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
