[深度学习][LLM]:浮点数怎么表示,什么是混合精度训练?
混合精度训练
- 混合精度训练
- 1. 浮点表示法:[IEEE](https://zh.wikipedia.org/wiki/电气电子工程师协会)二进制浮点数算术标准(IEEE 754)
- 1.1 浮点数剖析
- 1.2 举例说明
- 例子 1:
- 例子 2:
- 1.3 浮点数比较
- 1.4 浮点数的舍入
- 2. 混合精度训练
- 2.1 为什么需要半精度
- 2.2 FP16带来的问题:[量化误差](https://zhida.zhihu.com/search?q=量化误差&zhida_source=entity&is_preview=1)
- 2.3 FP32 权重备份
- 2.4 Loss Scale
- 2.5 提高算数精度
在日常深度学习训练中,一般使用单精度浮点数(float:FP32) 来表示参数并进行相关训练任务。那么浮点数在内存中是如何存储的呢?
在正式开始介绍混合精度训练之前,让我们先对半精度(FP16)、单精度(FP32)、双精度(FP64) 相关基础知识进行介绍。
1. 浮点表示法:IEEE二进制浮点数算术标准(IEEE 754)
IEEE二进制浮点数算术标准(IEEE 754)是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用。这个标准定义了表示浮点数的格式(包括负零-0)与反常值(denormal number),一些特殊数值((无穷(Inf)与非数值(NaN)),以及这些数值的“浮点数运算符”;它也指明了四种数值舍入规则和五种例外状况(包括例外发生的时机与处理方式)。
1.1 浮点数剖析
一个浮点数 (Value) 的表示其实可以这样表示:
Value=sign × exponent × fraction 1. M . . . × 2 E , E = exponent ; M = fraction \text{Value=sign} \times \text{exponent} \times \text{fraction} \\ 1.M... \times2^E,E=\text{exponent};M=\text{fraction} Value=sign×exponent×fraction1.M...×2E,E=exponent;M=fraction
也就是浮点数的实际值,等于符号位(sign bit)乘以指数偏移值(exponent bias)再乘以分数值(fraction)。
二进制浮点数是以符号数值表示法的格式存储——最高有效位被指定为符号位(sign bit);“指数部分”,即次高有效的e个比特,存储指数部分;最后剩下的f个低有效位的比特,存储“有效数”(significand)的小数部分。

指数部分,也称为指数偏移值(exponent bias),即浮点数表示法中指数域的编码值,等于指数的实际值加上某个固定的值,IEEE 754标准规定该固定值为 2 e − 1 − 1 2^{e−1}−1 2e−1−1其中的 e e e 为存储指数的比特的长度。
以单精度浮点数为例,它的指数域是8个比特,固定偏移值是 2 8 − 1 − 1 = 128 − 1 = 127 2^{8−1}−1=128−1=127 28−1−1=128−1=127,单精度浮点数的指数部分 E E E,实际取值是从-126到127(-127和128被用作特殊值处理)
采用指数的实际值加上固定的偏移值的办法表示浮点数的指数,好处是可以用长度为 e e e 个比特的无符号整数来表示所有的指数取值,这使得两个浮点数的指数大小的比较更为容易,实际上可以按照字典次序比较两个浮点表示的大小。
这种移码表示的指数部分,中文称作阶码。
特殊值:
这里有三个特殊值需要指出:
- 如果指数是0并且尾数的小数部分是0,这个数±0(和符号位相关): s i g n × 0.0 × 2 − 127 sign \times0.0\times2^-{127} sign×0.0×2−127
- 如果指数 = 2 e − 1 = 2^{e−1} =2e−1 并且尾数的小数部分是0,这个数是±∞(同样和符号位相关): s i g n × 0.0 × 2 128 sign\times0.0\times2^{128} sign×0.0×2128
- 如果指数 = 2e−1并且尾数的小数部分非0,这个数表示为非数(NaN): s i g n × 0. x x . . . × 2 128 sign\times0.xx...\times2^{128} sign×0.xx...×2128
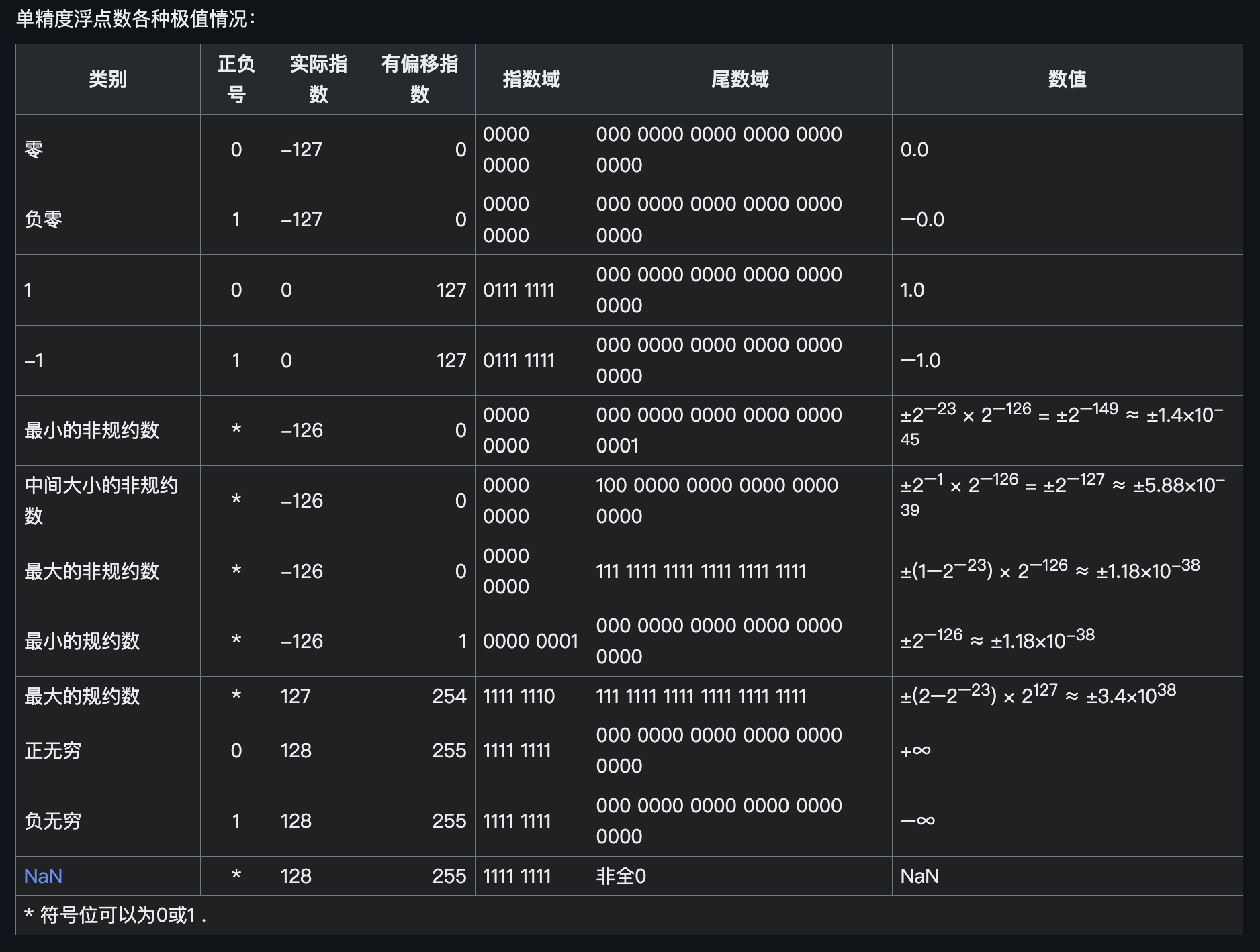
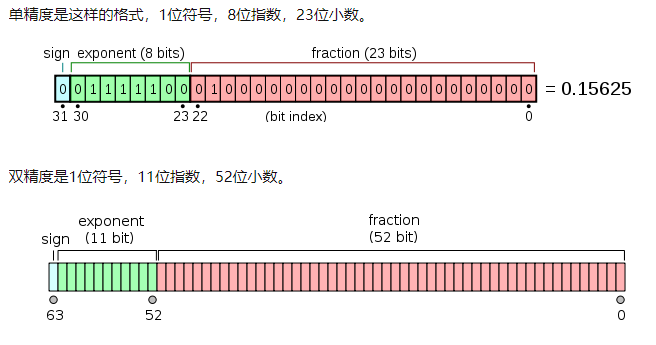
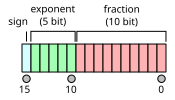
- 浮点数如何在计算机中储存,即**符号位,指数位,小数位(通常翻译为尾数)**取值范围取决于指数位,计算精度取决于小数位(尾数)。
- 小数位越多(比如双精度是52位),则能表示的数越大,那么计算精度则越高。单精度的小数位在计算机中只有23位(二进制),换算到十进制只能百分百保证6位十进制数字的精确度。不能百分百保证7位的精度运算。超过该精度(二进制23位,十进制6位)的小数运算将会被截取,造成精度损失和计算结果的不准确。同理,双精度,小数位是52位(二进制),换算为十进制则只能百分百能保证15位。
-
float16的精度是3-4位有效数字,取值范围为 [ − 65504 , 65504 ] [-65504,65504] [−65504,65504],占用2字节(8位)
-
float32的精度是6位有效数字,取值范围是 1 0 − 38 10^{-38} 10−38到 1 0 38 10^{38} 1038次方,float占用4字节空间(32位)
-
double的精度是15位有效数字,取值范围是 1 0 − 308 10^{-308} 10−308到 1 0 308 10^{308} 10308次方,double占用8字节空间(64位)。
1.2 举例说明
那一个小数到底要怎么换算成二进制呢?我们得拿实际例子来解释。
例子 1:
比如:把十进制小数0.875转换成二进制,具体怎么操作?
可以分几大步走:
1、以小数点为界,拆分
2、整数部分转换
整数转二进制我想大家应该都熟悉,使用:除2取余法 即可。而这里的0.875整数部分为0,无需操作。
3、小数部分转换
小数部分的转换不同于整数部分,采用的是 “乘2取整法” ,图示一下就明白了:
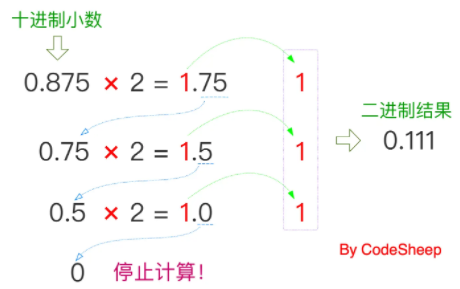
4、合并结果
整数部分 + 小数部分,最终得到二进制结果为0.111。
所以该结果按照上一节所述的尾数 + 阶码的计算机计数方式和上述公式对齐,小数点右移一位,则可以表示为:
1.11 × 2 − 1 1.11\times 2^{-1} 1.11×2−1
所以对应可得:
- 符号位:
0正数 - 阶码(E)部分:若以
float为例,固定偏移值为127,应为127 +(-1)= 126或者直接二进制相加,因此二进制表示为:01111110 - 尾数部分(M):若以
float为例,应为23位,因此尾部补齐后为11000000000000000000000。
因此最终的总结果为(以32位精度float表示):
00111111011000000000000000000000
例子 2:
再比如:把十进制小数6.36转换成二进制,具体怎么操作?
但凡能用图示,我就不想写文字,所以用一张图就可以解释得明明白白:

整数部分 + 小数部分,因此最终得到的结果二进制结果为110.01011100...。
还是按照上一节所述的尾数 + 阶码的计算机计数方式,小数点左移两位,则可以表示为:
1.1001011100... × 2 2 1.1001011100...\times2^{2} 1.1001011100...×22
所以对应可得:
- 符号位:
0 - 阶码(E)部分:若以
float为例,应为127 +(2)= 129,因此二进制表示为:10000001 - 尾数部分(M):
1001011100...,其实它本身无限不循环,但若以float型精度来截取23位,则可以表示为10010111000010100011111
因此最终的总结果为(以32位精度float表示):
01000000110010111000010100011111
所以像这种无限位数的尾数情况,用计算机存储产生截取是必然的,必定会有一定的精度损失!所以这也从根本上解释了为什么float或者double这种类型数据使用时的风险性,因此必须要结合实际业务理性考量。
1.3 浮点数比较
浮点数基本上可以按照符号位、指数域、尾数域的顺序作字典比较。显然,所有正数大于负数;正负号相同时,指数的二进制表示法更大的其浮点数值更大。
1.4 浮点数的舍入
任何有效数上的运算结果,通常都存放在较长的寄存器中,当结果被放回浮点格式时,必须将多出来的比特丢弃。 有多种方法可以用来执行舍入作业,实际上IEEE标准列出4种不同的方法:
- 舍入到最接近:舍入到最接近,在一样接近的情况下偶数优先(Ties To Even,这是默认的舍入方式):会将结果舍入为最接近且可以表示的值,但是当存在两个数一样接近的时候,则取其中的偶数(在二进制中是以0结尾的)。
- 朝+∞方向舍入:会将结果朝正无限大的方向舍入。
- 朝-∞方向舍入:会将结果朝负无限大的方向舍入。
- 朝0方向舍入:会将结果朝0的方向舍入。
2. 混合精度训练
该篇内容摘自:https://zhuanlan.zhihu.com/p/103685761
在这里的混合精度训练,指代的是单精度 float和半精度 float16 混合。比较经典的就是这篇ICLR2018,百度和Nvidia联合推出的论文 MIXED PRECISION TRAINING。 因此,这里也以这篇论文作为引子,对混合精度进行讲解。
2.1 为什么需要半精度
float16和float的优势,总结下来就是两个方面:内存占用更少,计算更快。
-
内存占用更少: 这个是显然可见的,通用的模型 fp16 占用的内存只需原来的一半。memory-bandwidth 减半所带来的好处:
-
- 模型占用的内存更小,训练的时候可以用更大的batchsize。
- 模型训练时,通信量(特别是多卡,或者多机多卡)大幅减少,大幅减少等待时间,加快数据的流通。
-
计算更快:
-
- 目前的不少GPU都有针对 fp16 的计算进行优化。论文指出:在近期的GPU中,半精度的计算吞吐量可以是单精度的 2-8 倍;
2.2 FP16带来的问题:量化误差
那么使用FP16的时候有没有什么问题呢?当然有。FP16带来的问题主要有两个:
- 溢出错误;
- 舍入误差。
- 溢出错误(Grad Overflow / Underflow) 由于FP16的动态范围( 6×10−8∼65504 )比FP32的动态范围( 1.4×10−45∼1.7×1038 )要狭窄很多,因此在计算过程中很容易出现上溢出(Overflow, g>65504 )和下溢出(Underflow, g<6×10−8 )的错误,溢出之后就会出现“Nan”的问题。在深度学习中,由于激活函数的的梯度往往要比权重梯度小,更易出现下溢出的情况。

2. 舍入误差(Rounding Error) 舍入误差指的是当梯度过小,小于当前区间内的最小间隔时,该次梯度更新可能会失败,用一张图清晰地表示:

这是因为FP16的最小间隔是一个比较玄乎的事,在wikipedia的引用上有这么一张图: 描述了 fp16 各个区间的最小gap。

2.3 FP32 权重备份
这种方法主要是用于解决舍入误差的问题。其主要思路,可以概括为:weights, activations, gradients 等数据在训练中都利用FP16来存储,同时拷贝一份FP32的weights,用于更新。 在这里,我直接贴一张论文[1]的图片来阐述:
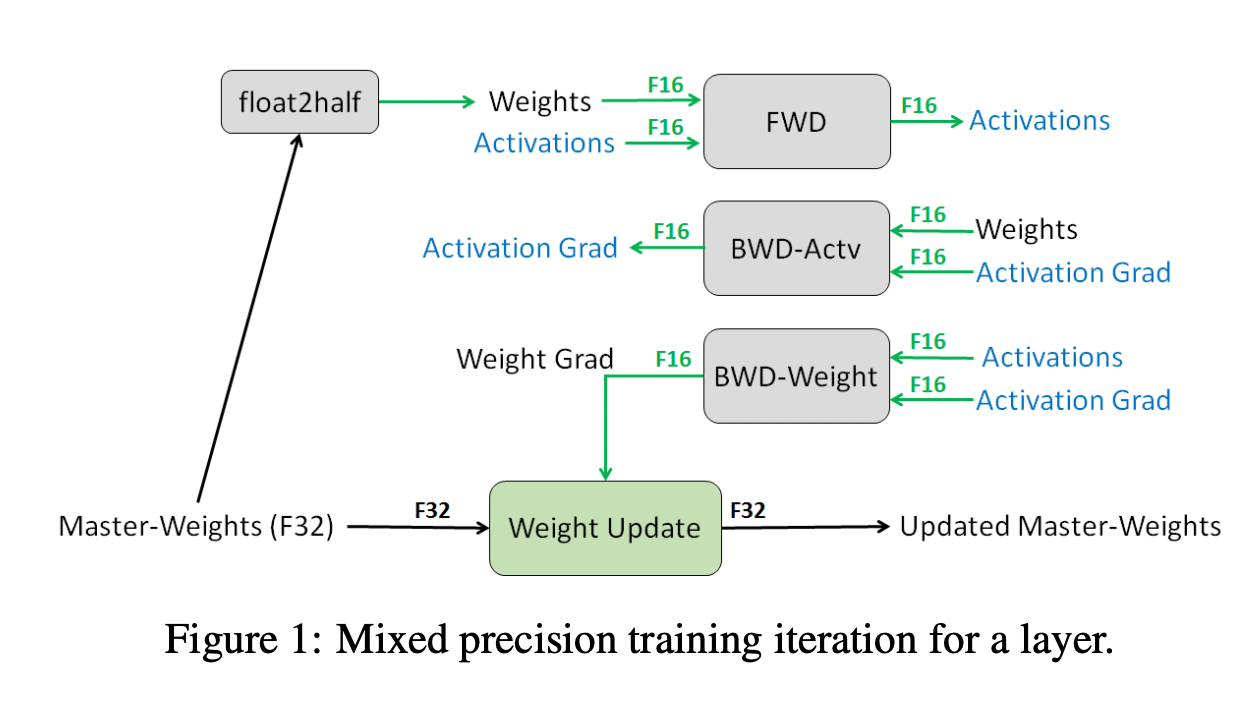
可以看到,其他所有值(weights,activations, gradients)均使用 fp16 来存储,而唯独权重weights需要用 fp32 的格式额外备份一次。 这主要是因为,在更新权重的时候,往往公式: 权重 = 旧权重 + lr * 梯度,而在深度模型中,lr * 梯度 这个值往往是非常小的,如果利用 fp16 来进行相加的话, 则很可能会出现上面所说的『舍入误差』的这个问题,导致更新无效。因此上图中,通过将weights拷贝成 fp32 格式,并且确保整个更新(update)过程是在 fp32 格式下进行的。
看到这里,可能有人提出这种 fp32 拷贝weight的方式,那岂不是使得内存占用反而更高了呢?是的, fp32 额外拷贝一份 weight 的确新增加了训练时候存储的占用。 但是实际上,在训练过程中,内存中占据大部分的基本都是 activations 的值。特别是在batchsize 很大的情况下, activations 更是特别占据空间。 保存 activiations 主要是为了在 back-propogation 的时候进行计算。因此,只要 activation 的值基本都是使用 fp16 来进行存储的话,则最终模型与 fp32 相比起来,内存占用也基本能够减半。
此时所存储的参数为;
FP16: weights,activations,gradients
FP32: weights,gradients
2.4 Loss Scale
Loss Scale 主要是为了解决 fp16 underflow 的问题。刚才提到,训练到了后期,梯度(特别是激活函数平滑段的梯度)会特别小,fp16 表示容易产生 underflow 现象。 下图展示了 SSD 模型在训练过程中,激活函数梯度的分布情况:可以看到,有67%的梯度小于 2−24 ,如果用 fp16 来表示,则这些梯度都会变成0。
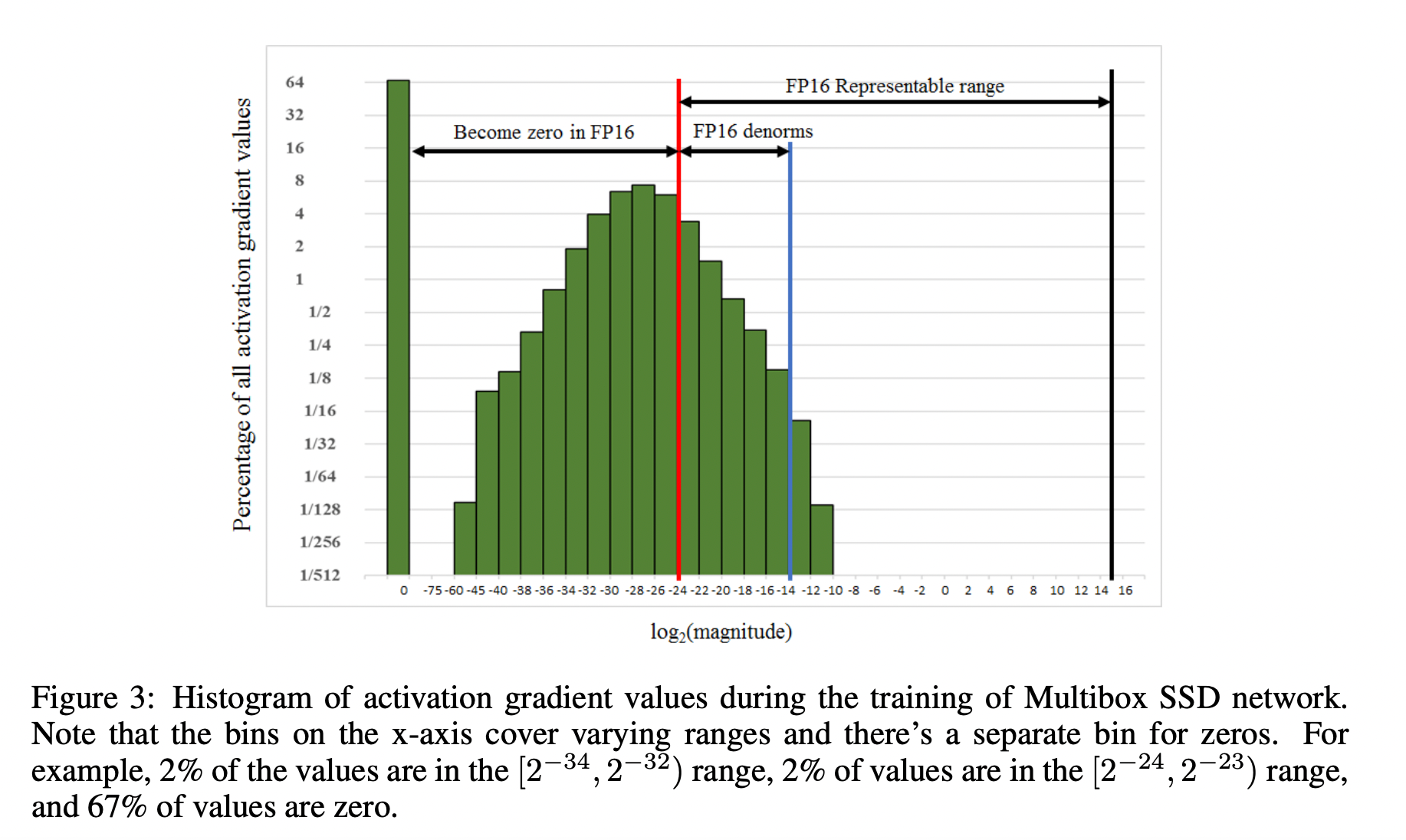
为了解决梯度过小的问题,论文中对计算出来的loss值进行scale,由于链式法则的存在,loss上的scale会作用也会作用在梯度上。这样比起对每个梯度进行scale更加划算。 scaled 过后的梯度,就会平移到 fp16 有效的展示范围内。
这样,scaled-gradient 就可以一直使用 fp16 进行存储了。只有在进行更新的时候,才会将 scaled-gradient 转化为 fp32,同时将scale抹去。论文指出, scale 并非对于所有网络而言都是必须的。而scale的取值为也会特别大,论文给出在 8 - 32k 之间皆可。
2.5 提高算数精度
在论文中还提到一个『计算精度』的问题:在某些模型中,fp16矩阵乘法的过程中,需要利用 fp32 来进行矩阵乘法中间的累加(accumulated),然后再将 fp32 的值转化为 fp16 进行存储。 换句不太严谨的话来说,也就是利用 利用fp16进行乘法和存储,利用fp32来进行加法计算。 这么做的原因主要是为了减少加法过程中的舍入误差,保证精度不损失。
在这里也就引出了,为什么网上大家都说,只有 Nvidia Volta 结构的 拥有 TensorCore 的CPU(例如V100),才能利用 fp16 混合精度来进行加速。 那是因为 TensorCore 能够保证 fp16 的矩阵相乘,利用 fp16 or fp32 来进行累加。在累加阶段能够使用 FP32 大幅减少混合精度训练的精度损失。而其他的GPU 只能支持 fp16 的 multiply-add operation。这里直接贴出原文句子:
Whereas previous GPUs supported only FP16 multiply-add operation, NVIDIA Volta GPUs introduce Tensor Cores that multiply FP16 input matrices andaccumulate products into either FP16 or FP32 outputs
相关文章:

[深度学习][LLM]:浮点数怎么表示,什么是混合精度训练?
混合精度训练 混合精度训练1. 浮点表示法:[IEEE](https://zh.wikipedia.org/wiki/电气电子工程师协会)二进制浮点数算术标准(IEEE 754)1.1 浮点数剖析1.2 举例说明例子 1:例子 2: 1.3 浮点数比较1.4 浮点数的舍入 2. 混合精度训练2.1 为什么需…...

openssl双向认证自签名证书生成
编写配置文件openssl.cnf [ req ] distinguished_name req_distinguished_name req_extensions req_ext[ req_distinguished_name ] countryName Country Name (2 letter code) countryName_default US stateOrProvinceName State or Province Name…...

如何使用 Python 读取 Excel 文件:从零开始的超详细教程
“日出东海落西山 愁也一天 喜也一天 遇事不钻牛角尖” 文章目录 前言文章有误敬请斧正 不胜感恩!||Day03为什么要用 Python 读取 Excel 文件?准备工作:安装所需工具安装 Python安装 Pandas安装 openpyxl 使用 Pandas 读取 Excel 文件什么是 …...

仕考网:公务员笔试和面试哪个难?
公务员笔试和面试哪个难?二者之间考察的方向不同,难度也是不同的。 笔试部分因其广泛的知识点和有限的考试时间显得难度更高一些,在笔试环节中,考生需在有限的时间内应对各种问题,而且同时还要面对激烈的竞争,在众多…...
:时间优化)
C++知识点总结(55):时间优化
时间优化 一、调试方法1. 输出调试2. 构造样例 二、时间优化1. 前缀和1.1 概念1.2 例题Ⅰ 区间最多数码Ⅱ 双字母字符串Ⅲ Wandering...Ⅳ 数对数目 2. 排序例题选择排序过程 一、调试方法 1. 输出调试 cout 是一个强大的调试工具,可以帮助我们查看程序的状态和变…...
)
GitHub每日最火火火项目(9.7)
项目名称:polarsource / polar 项目介绍:polar 是一个开源的项目,它是 Lemon Squeezy 的替代方案,具有更优惠的价格。该项目旨在让开发者能够凭借自己的热情进行编码并获得报酬。通过使用 polar,开发者可以更轻松地实现…...

11Python的Pandas:可视化
Pandas本身并没有直接的可视化功能,但它与其他Python库(如Matplotlib和Seaborn)无缝集成,允许你快速创建各种图表和可视化。这里是一些使用Pandas数据进行可视化的常见方法: 1. 使用Matplotlib Pandas中的plot()方法…...

【周易哲学】生辰八字入门讲解(二)
😊你好,我是小航,一个正在变秃、变强的文艺倾年。 🔔本文讲解【周易哲学】生辰八字入门讲解,期待与你一同探索、学习、进步,一起卷起来叭! 目录 十神十神判断十神类象十神与五行案例 地支藏干藏…...

传统CV算法——基于Opencv的多目标追踪算法
基于 OpenCV 的跟踪算法有多种,每种算法都有其特定的应用场景和优缺点。以下是一些常见的基于 OpenCV 的目标跟踪算法: 1. BOOSTING 跟踪器 描述:基于 AdaBoost 算法的跟踪器。它是一种早期的跟踪算法,使用的是基于弱分类器的强…...

人生苦短我用Python excel转csv
人生苦短我用Python excel转csv 前言准备工作pandas库主要类和方法ExcelFile 类DataFrame 类read_excel 函数to_csv 函数 示例 前言 Excel 文件和csv文件都是常用的电子表格文件格式,其中csv格式更便于用于数据交换和处理。本文使用pandas库将Excel文件转化为csv文…...

Web2和Web3笔记
KimiAI: Web2和Web3是互联网发展的不同阶段,它们代表了不同的技术、理念和用户交互方式。 Web2: Web2通常指的是第二代互联网,它始于2000年代中期,以用户生成内容和社交网络的兴起为标志。 在Web2中,用户不仅是内容的消…...

单元测试 Mock不Mock?
文章目录 前言单元测试没必要?Mock不Mock?什么是Mock?Mock的意义何在? 如何Mock?应该Mock什么?Mock 编写示例 总结 前言 前段时间,我们团队就单元测试是否采用 Mock 进行了一番交流,各有各的说法。本文就单元测试 Mock不Mock…...

常用排序算法(上)
目录 前言: 1.排序的概念及其运用 1.1排序的概念 1.2排序运用 1.3 常见的排序算法 2.常见排序算法的实现 2.1 堆排序 2.1 1 向下调整算法 2.1 2 建堆 2.1 3 排序 2.2 插入排序 2.1.1基本思想: 2.1.2直接插入排序: 2.1.3 插…...
(二十六))
【从问题中去学习k8s】k8s中的常见面试题(夯实理论基础)(二十六)
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...

小程序的页面跳转方式
102. 小程序的页面跳转方式 小程序是一种快速发展的应用形式,为用户提供了便捷的功能和交互体验。其中,页面跳转是小程序中常用的功能之一,本文将介绍小程序的页面跳转方式,并提供代码示例,帮助读者更好地理解和实现页…...

第 21 章 DOM 操作表格及样式
第 21 章 DOM 操作表格及样式 1.操作表格 2.操作样式 DOM 在操作生成 HTML 上,还是比较简明的。不过,由于浏览器总是存在兼容和陷阱,导致最终的操作就不是那么简单方便了。本章主要了解一下 DOM 操作表格和样式的一些知识。 一࿰…...

vc-align源码分析 -- ant-design-vue系列
vc-align源码分析 源码地址:https://github.com/vueComponent/ant-design-vue/tree/main/components/vc-align 1 基础代码 1.1 名词约定 需要对齐的节点叫source,对齐的目标叫target。 1.2 props 提供了两个参数: align:对…...

计算机网络(四) —— 简单Tcp网络程序
目录 一,服务器初始化 1.0 部分文件代码 1.1 关于Tcp协议 1.2 创建和绑定套接字 1.3 监听 二,服务器启动 2.1 获取连接 2.2 提供服务 2.3 客户端启动源文件 Main.cc 二,客户端编写 2.1 关于Tcp客户端 2.2 客户端代码 2.3 效果…...

简单的Linux Ftp服务搭建
简单的Linux FTP服务搭建 1.需求 公司有一个esb文件传输代理,其中我们程序有文件传输功能,需要将本地文件传输到esb文件代理服务器上,传输成功之后发送http请求,告知esb将固定文件进行传输到对应外围其他服务的文件目录中&#…...
SQL的高级查询练习知识点(day24)
目录 1 学习目标 2 基础查询 2.1 语法 2.2 例子 3 条件查询 3.1 含义 3.2 语法 3.3 条件表达式 3.3.1 条件运算符 3.3.2 例子 3.4 逻辑表达式 3.4.1 逻辑运算符 3.4.2 例子 3.5 模糊查询 3.5.1 概述 3.5.2 例子 4 DISTINCT关键字 4.1 含义 4.2 例子 5 总结…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
