常用排序算法(上)
目录
前言:
1.排序的概念及其运用
1.1排序的概念
1.2排序运用
1.3 常见的排序算法
2.常见排序算法的实现
2.1 堆排序
2.1 1 向下调整算法
2.1 2 建堆
2.1 3 排序
2.2 插入排序
2.1.1基本思想:
2.1.2直接插入排序:
2.1.3 插入排序实现
2.3 希尔排序
2.4 选择排序
2.4.1基本思想:
2.4.2 直接选择排序:
2 .4.3 选择排序实现
前言:
当我们学到数据结构时,就无法避开算法,排序是一类常见且常用的算法,在日常生活中,我们在网上购物,筛选价格时用到了排序,查看该商品销量的高低时用到了排序,而这些功能都是我们程序员使用排序算法将其转化成代码实现的。既然排序如此重要,我们当然要好好把排序学好了。
1.排序的概念及其运用
1.1排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不断地在内外存之间移动数据的排序。
1.2排序运用
排序的重要性在前面我们已经讲解,在这里就不再过多赘述。


1.3 常见的排序算法
在学习排序算法之前,我们应该了解常见的排序算法有哪些,排序一般分为插入排序,选择排序,交换排序,归并排序,而细分的话可以分成下面的样子:

2.常见排序算法的实现
2.1 堆排序
堆排序我们在学习二叉树堆时,已经讲过了,将它放在这里,一是复习一遍堆排序,二是将这些排序都总结在一起,方便我们查看。堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。

简单来说,堆排序的算法就是先建一个堆,如果我们要排升序就建大堆,将堆最大的那个数——也就是根节点中的那个数与堆尾交换,这样最大的数就排到最后一位了,此时的数组已经不是堆了,我们使用向下调整算法重新建堆,这样数组中第二大的数就在根结点中了,我们再将它和堆倒数第二个位置的数交换,这样第二大的数就在数组倒数第二的位置了,像这样一种走到根节点,我们也就完成了排序的操作。
2.1 1 向下调整算法
第一个双亲结点默认是数组中下标为0的位置,我们需要算出它的孩子结点,而公式也个很简单,双亲*2+1就是这个结点的左孩子,双亲*2+2就是这个结点的右孩子。假设我们建的是大堆,双亲结点比孩子结点小就交换,我们默认这棵树是完全二叉树,所以大多数结点都有两个孩子,我们需要选出两个孩子结点中大的那个与双亲结点交换位置,交换完就刷新双亲结点和子节点的下标,而前提是两个结点都在数组中,所以有:
int child = parent * 2 + 1;
//假设左孩子就是要交换的那个孩子
if (child + 1 < n && a[child + 1] > a[child])
{child++;
}
//如果某个结点比左孩子小,而右孩子比左孩子大,
//就让该节点的右孩子与自己交换位置我们设置一个循环,如果某个结点的孩子的下标大于等于n,说明我们已经完成了交换,就不进入循环,如果发现这是一个堆,就跳出循环:
void AdjustDown(int* a, size_t n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}}2.1 2 建堆
给我们一组无序的数字,我们采用从后往前向下调整的方法来建堆。如果我们将这组数据看成完全二叉树,除了叶子结点,其余的结点都有孩子,也就是说,有几个有孩子结点的结点,这组数据中就有几棵树,我们可以从最后一个有孩子结点的结点开始使用向下调整算法,当走到这棵树的根节点时,就将堆建好了:

例如这棵树,从9这个结点开始,往前都可以组成一棵树,而如何得到呢,这个也很简单,我们只需要反转计算孩子结点的公式,得到计算双亲结点的公式为(孩子-1)÷ 2 ,假设这棵树有n个结点,这棵树的尾结点为n-1,所以假设我们要得到9这个结点,公式为:(n-1-1)÷2。
得到代码:
for (int i = (size - 1 - 1) / 2; i >= 0; i--)
{AdjustDown(a, size, i);
}2.1 3 排序
建好堆之后,我们就可以排序了,按前面讲的排,得到代码:
//定义一个end方便交换,每次交换完往前走一步
int end = size - 1;
//size为数组大小
while (end > 0)
{Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;
}堆排序完整代码:
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustDown(int* a, size_t n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}}我们定义一个数组,给一些数测数一下:
int a[] = { 454,24,34,43543,676,67,676,23,1,0 };
size_t size = sizeof(a) / sizeof(int);
HeapSort(a, size);
for (int i = 0; i < size; i++)
{printf("%d ", a[i]);
}
可以看到,一个有序的数组就完成了。
2.2 插入排序
2.1.1基本思想:
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际中我们玩扑克牌时,就用了插入排序的思想

2.1.2直接插入排序:
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移:

直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
2.1.3 插入排序实现
我们定义一个end,在end下标及end之前下标的数都是有序的数,依次从end之后取数据来插入end之前,如果我们要排升序,我们从end+1开始取数据存起来,只要这个数小于end,就让end覆盖end+1,然后让end向前走一位,直到这个数比end下标的数大或者等于这个数,我们让end往前走一位,然后将这个数插入到end+1的位置。以上是一轮插入,要实现插入排序需要让end走遍整个数组,而每次插入都只插入一个数,假设某个数据为n,那么当执行完end=n-2时,这个数组也就有序了,代码展示:
void InsertSort(int* a, size_t n)
{int end;int tmp;for (int i = 0; i < n - 1; i++){end = i;tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}}我们准备一个无序数组,调用插入排序:
int a[] = { 9,8,7,6,5,4,3,2,4,5,98,43,67,879,4543,687686,676,1,0 };
size_t size = sizeof(a) / sizeof(a[0]);
InsertSort(a, size);来看结果:

调用插入排序后,这个数组就被排成了升序。
2.3 希尔排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。本质上,希尔排序是对插入排序的优化。

先对一组数进行预排序,再对这组数据进行插入排序,这就是希尔排序。而上面的操作就是对这组数据进行预排序,预排序可以让一个很大或者很小的数更快走到它排序之后的位置,假如gap=5,我们需要排升序,整个数组中最大的数只需要走两次就可以走到最后一个位置。事实上,插入排序就是希尔排序当gap为1时,一个数一次只能走1步。因此,我们得出:gap越大,大数越快走到后面,小数越快走到后面,越不接近有序。为什么呢?因为当gap=1时,执行这个程序,该组数据就有序了,所以:gap越小,大数越满走到后面,小数越慢走到前面,数组却越接近有序。
希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些书中给出的希尔排序的时间复杂度都不固定:

数据结构-用面相对象方法与C++描述》--- 殷人昆

4.稳定性:不稳定
2.4 选择排序
2.4.1基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
2.4.2 直接选择排序:
(1)在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
(2)若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
(3)在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素

2 .4.3 选择排序实现
在我们的介绍中,选择排序就是我们多次遍历一个数组,如果要排升序,那么第一次遍历出来最小的数放到第一位,第二次遍历出来最小的数放到第二位,依次遍历完整个数组就完成了排序。我们可以对其优化一下,定义一个max和min,也就是每一次遍历都选出最小的数和最大的数,最小的数放在最前面,最大的数放在最后面,依次执行,像这样优化的速度是普通选择排序的2倍。
定义一个起始位置的下标begin和末尾位置的下标end,接着是max和min,从begin+1的位置开始往前走,让max,min下标的数与整个数组的其他数比较,只要有比max大的数就让那个数成为max,只要有比min小的数就让这个数成为min,遍历完一遍后,让begin下标的数和min下标的数交换,接着让end下标的数和max下标的数交换,这样最大的数和最小的数都排好了,让begin往前走一步,end往后走一步,做完这些后,让max和min重新从begin们开始走,代码实现:
void SecletSort(int* a, size_t n)
{int begin = 0, end = n - 1;int maxi = begin;int mini = begin;while (begin < end){mini = begin;maxi = begin;for (int i = begin + 1; i <= end; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[mini], &a[begin]);if (begin == maxi)maxi = mini;Swap(&a[maxi], &a[end]);begin++;end--;}}依旧是一组无序的数,调用选择排序:
int a[] = { 9,8,7,6,5,4,3,2,4,5,98,43,67,879,4543,687686,676,1,0 };
size_t size = sizeof(a) / sizeof(a[0]);
SecletSort(a, size);来看结果:

选择排序也没有任何问题,将一组无序数排成升序。
未完待续。。。。。。
相关文章:

常用排序算法(上)
目录 前言: 1.排序的概念及其运用 1.1排序的概念 1.2排序运用 1.3 常见的排序算法 2.常见排序算法的实现 2.1 堆排序 2.1 1 向下调整算法 2.1 2 建堆 2.1 3 排序 2.2 插入排序 2.1.1基本思想: 2.1.2直接插入排序: 2.1.3 插…...
(二十六))
【从问题中去学习k8s】k8s中的常见面试题(夯实理论基础)(二十六)
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...

小程序的页面跳转方式
102. 小程序的页面跳转方式 小程序是一种快速发展的应用形式,为用户提供了便捷的功能和交互体验。其中,页面跳转是小程序中常用的功能之一,本文将介绍小程序的页面跳转方式,并提供代码示例,帮助读者更好地理解和实现页…...

第 21 章 DOM 操作表格及样式
第 21 章 DOM 操作表格及样式 1.操作表格 2.操作样式 DOM 在操作生成 HTML 上,还是比较简明的。不过,由于浏览器总是存在兼容和陷阱,导致最终的操作就不是那么简单方便了。本章主要了解一下 DOM 操作表格和样式的一些知识。 一࿰…...

vc-align源码分析 -- ant-design-vue系列
vc-align源码分析 源码地址:https://github.com/vueComponent/ant-design-vue/tree/main/components/vc-align 1 基础代码 1.1 名词约定 需要对齐的节点叫source,对齐的目标叫target。 1.2 props 提供了两个参数: align:对…...

计算机网络(四) —— 简单Tcp网络程序
目录 一,服务器初始化 1.0 部分文件代码 1.1 关于Tcp协议 1.2 创建和绑定套接字 1.3 监听 二,服务器启动 2.1 获取连接 2.2 提供服务 2.3 客户端启动源文件 Main.cc 二,客户端编写 2.1 关于Tcp客户端 2.2 客户端代码 2.3 效果…...

简单的Linux Ftp服务搭建
简单的Linux FTP服务搭建 1.需求 公司有一个esb文件传输代理,其中我们程序有文件传输功能,需要将本地文件传输到esb文件代理服务器上,传输成功之后发送http请求,告知esb将固定文件进行传输到对应外围其他服务的文件目录中&#…...
SQL的高级查询练习知识点(day24)
目录 1 学习目标 2 基础查询 2.1 语法 2.2 例子 3 条件查询 3.1 含义 3.2 语法 3.3 条件表达式 3.3.1 条件运算符 3.3.2 例子 3.4 逻辑表达式 3.4.1 逻辑运算符 3.4.2 例子 3.5 模糊查询 3.5.1 概述 3.5.2 例子 4 DISTINCT关键字 4.1 含义 4.2 例子 5 总结…...

Python条件表达式优化的10个实例
Python 中的条件表达式(也称为三元运算符)是一种简洁的语法,用于在单个表达式中执行 if-else 逻辑。虽然它们本身并不直接“优化”代码的执行速度,但它们可以使代码更加简洁、易读,并且有助于避免不必要的嵌套或复杂的…...

oatpp apiclient 客户端get,post请求python fastapi demo
最新用fastapi搞了个服务端,python功能太强了,就是环境不好弄,弄好后,不要轻易换python版本,不要装多个python版本 前面搞了个oatpp webapi服务端,现在要用客户端,为什么用opatpp客户端,因为他不再带其他库了 demo: 我的请求比较简单,就是向python 的 fastapi服务端…...
EMMC介绍)
RK3568平台(内存篇)EMMC介绍
一.eMMC是什么 eMMC (Embedded Multi Media Card)是MMC协会订立、主要针对手机或平板电脑等产品的内嵌式存储器标准规格。由一个嵌入式存储解决方案组成,带有MMC(多媒体卡)接口、快闪存储器设备及主控制器。所有都在一个小型的BGA 封装。接口速度高达每秒52MBytes,eMMC具…...
Python批量读取身份证信息录入系统和重命名
前言 大家好, 如果你对自动化处理身份证图片感兴趣,可以尝试以下操作:从身份证图片中快速提取信息,填入表格并提交到网页系统。如果你无法完成这个任务,我们将在“Python自动化办公2.0”课程中详细讲解实现整个过程。…...

IBM Storwize V7000存储控制器故障节点报错574
背景:由于客户机房搬迁,需要下电迁移设备。该存储自2016年投入生产使用后,从未关过机,已正常运行七八年时间,期间只更换过硬盘,无其他硬件故障。 在GUI界面点击关闭系统后,大概等了40分钟&…...

通信工程学习:什么是SSB单边带调制、VSB残留边带调制、DSB抑制载波双边带调制
SSB单边带调制、VSB残留边带调制、DSB抑制载波双边带调制 SSB单边带调制、VSB残留边带调制、DSB抑制载波双边带调制是三种不同的调制方式,它们在通信系统中各有其独特的应用和特点。以下是对这三种调制方式的详细解释: 一、SSB单边带调制 1、SSB单边带…...

MapSet之二叉搜索树
系列文章: 1. 先导片--Map&Set之二叉搜索树 2. Map&Set之相关概念 目录 前言 1.二叉搜索树 1.1 定义 1.2 操作-查找 1.3 操作-新增 1.4 操作-删除(难点) 1.5 总体实现代码 1.6 性能分析 前言 TreeMap 和 TreeSet 是 Java 中基于搜索树实现的 M…...

OpenCV图像分割教程
OpenCV 图像分割教程 OpenCV 是一个非常强大的计算机视觉库,支持各种图像处理任务。图像分割是 OpenCV 支持的一个重要功能,它用于将图像划分为不同的区域,识别感兴趣的部分。我们将通过介绍 OpenCV 中的图像分割方法,包括基础功…...

python科学计算:NumPy 线性代数与矩阵操作
1 NumPy 中的矩阵与数组 在 NumPy 中,矩阵实际上是一种特殊的二维数组,因此几乎所有数组的操作都可以应用到矩阵上。不过,矩阵运算与一般的数组运算存在一定的区别,尤其是在点积、乘法等操作中。 1.1 创建矩阵 矩阵可以通过 Nu…...

Unity面向对象补全计划 之 List<T>与class(非基础)
C# & Unity 面向对象补全计划 泛型-CSDN博客 关于List,其本质就是C#封装好的一个数组,是一个很好用的轮子,所以并不需要什么特别说明 问题描述 假设我们有一个表示学生的类 Student,每个学生有姓名和年龄两个属性。我们需要创…...

ant design vue+vue3+ts+xlsx实现表格导出问excel文件(带自定义表头)~
1、首先默认你已安装ant design vue、xlsx 库、及file-saver。 2、导入: import * as XLSX from xlsx; import { saveAs } from file-saver; 注:这里的xlsx导入不能这么写,否则会报错,原因是版本不一致,语法向上兼容…...
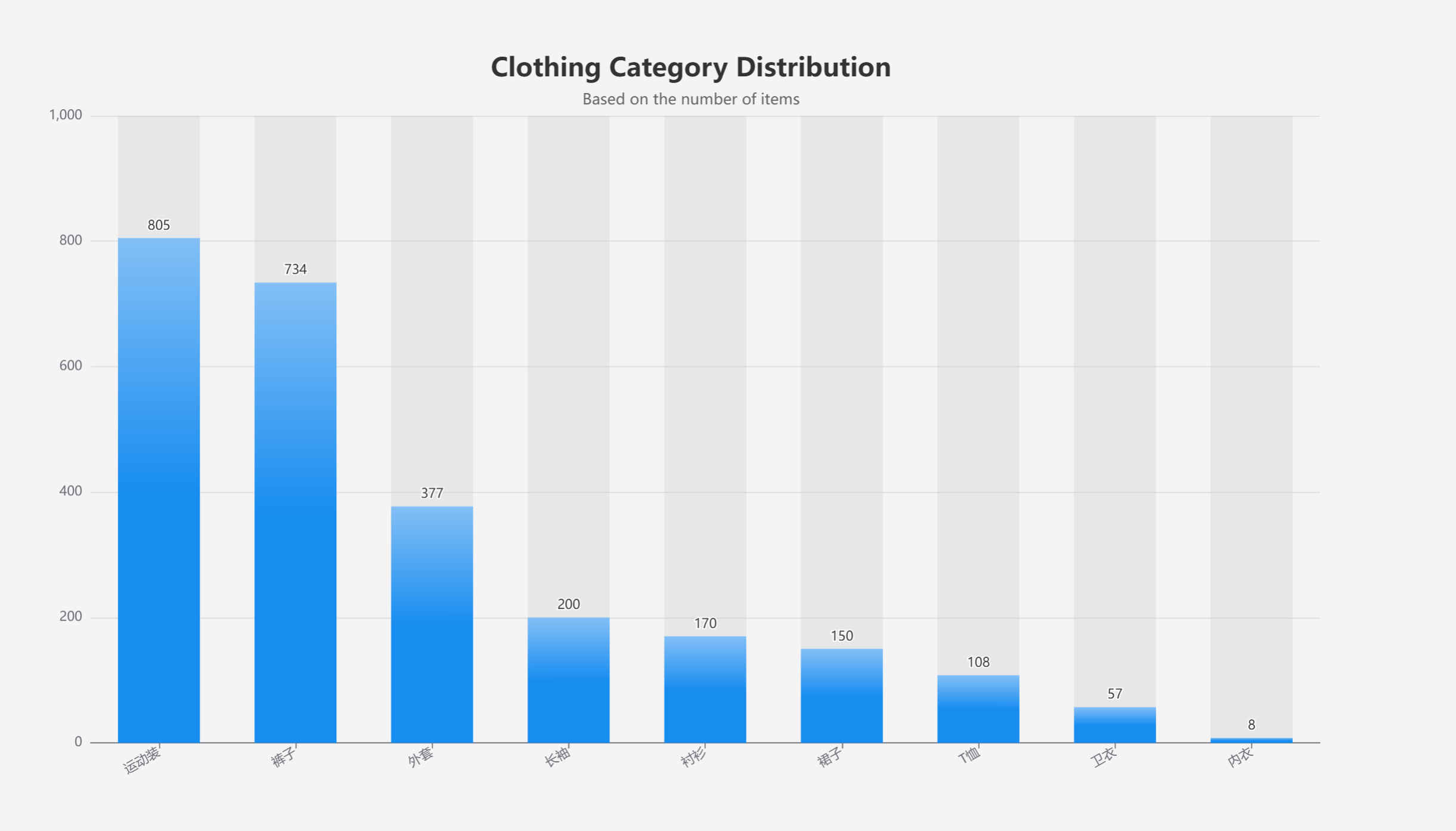
基于Python爬虫的淘宝服装数据分析项目
文章目录 一.项目介绍二.爬虫代码代码分析 三. 数据处理四. 数据可视化 一.项目介绍 该项目是基于Python爬虫的淘宝服装数据分析项目,以致于帮助商家了解当前服装市场的需求,制定更加精确的营销策略。首先,需要爬取淘宝中关于服装的大量数据…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
