AI学习指南深度学习篇-带动量的随机梯度下降法的基本原理
AI学习指南深度学习篇——带动量的随机梯度下降法的基本原理
引言
在深度学习中,优化算法被广泛应用于训练神经网络模型。随机梯度下降法(SGD)是最常用的优化算法之一,但单独使用SGD在收敛速度和稳定性方面存在一些问题。为了应对这些挑战,动量法应运而生。本文将详细介绍动量法的原理,包括动量的概念、指数加权移动平均、参数更新等内容,最后通过实际示例展示动量如何帮助SGD在参数更新过程中平稳地前进。
什么是动量?
动量最初是物理学中的一个概念,用于描述物体的运动。动量法在优化算法中引入了一个“动量”项,帮助在优化过程中加速以及平滑更新。动量可以看作是对过去梯度的“回忆”,这种技术使得优化算法能够在一定程度上克服SGD固有的震荡,并在某些方向上加速前进。
动量的基本想法
动量法利用了梯度的历史信息,通常通过对过去几次梯度更新的加权求和,来决定当前参数的更新方向。具体来说,当模型在某一方向上的梯度变化较小,而在另一个方向上的梯度变化较大时,动量法能够加快在有效方向上的更新,从而提高收敛速度。
在动量更新中,我们维护一个动量变量 (v),它根据历史梯度逐步更新。动量变量对当前梯度的影响越来越大,而对较久以前的梯度影响逐渐减小。
指数加权移动平均
动量法的核心在于指数加权移动平均(Exponential Moving Average,EMA)。通过对过去的梯度施加一个衰减因子,EMA 使得新的梯度对更新的影响更大,而较旧的梯度的影响逐渐减小。
公式表示
假设我们在第 (t) 次迭代中计算得到的梯度为 (g_t),动量变量 (v_t) 的更新公式为:
[ v t = β v t − 1 + ( 1 − β ) g t ] [ v_t = \beta v_{t-1} + (1 - \beta) g_t ] [vt=βvt−1+(1−β)gt]
其中, ( β ) (\beta) (β) 是动量系数,通常设置为接近于1(例如,0.9 或 0.99)。这样,动量变量 ( v t ) (v_t) (vt) 会逐渐地保留历史梯度信息,同时抑制噪声带来的干扰。参数的更新则通过以下公式完成:
[ θ t = θ t − 1 − α v t ] [ \theta_t = \theta_{t-1} - \alpha v_t ] [θt=θt−1−αvt]
这里, ( α ) (\alpha) (α) 是学习率。
动量在参数更新中的作用
在采用动量法后,参数更新的路径会更加平滑和稳定。具体来说,动量带来的优势主要体现在以下几个方面:
-
加速收敛:在深度的损失曲面中,有些方向会出现较大的梯度,而另一些方向的梯度可能会相对较小。动量方法通过对历史梯度的重置,能够在大的梯度方向上加速更新。
-
减小震荡:SGD 的震荡通常会导致模型难以在局部最优点附近平稳地收敛。动量法通过平滑的优化路径减少这种震荡,使得更新方向更加稳定。
-
逃离局部最优:通过保持较高的动量,有时候模型将能够逃离局部最优点,因为动量会推动参数在一定方向上继续移动。
实际示例
为了更好地理解和运用带动量的随机梯度下降法,我们将展示一个实际示例。假设我们要训练一个简单的线性回归模型,损失函数为均方误差(MSE)。
1. 线性回归模型
模型的预测公式为:
[ y ^ = w x + b ] [ \hat{y} = wx + b ] [y^=wx+b]
其中, ( w ) (w) (w) 是权重, ( b ) (b) (b) 是偏差。损失函数定义为:
[ L ( w , b ) = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 ] [ L(w, b) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 ] [L(w,b)=n1i=1∑n(yi−y^i)2]
2. 梯度计算
对于每个参数 (w) 和 (b),我们需要计算它们的梯度:
[ ∂ L ∂ w = − 2 n ∑ i = 1 n ( y i − y ^ i ) ⋅ x i ] [ \frac{\partial L}{\partial w} = -\frac{2}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i) \cdot x_i ] [∂w∂L=−n2i=1∑n(yi−y^i)⋅xi]
[ ∂ L ∂ b = − 2 n ∑ i = 1 n ( y i − y ^ i ) ] [ \frac{\partial L}{\partial b} = -\frac{2}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i) ] [∂b∂L=−n2i=1∑n(yi−y^i)]
3. 动量更新
在训练过程中,我们将使用动量方法更新权重和偏差。以下是代码示例(以 Python 和 NumPy 为例):
import numpy as np# 超参数
alpha = 0.01 # 学习率
beta = 0.9 # 动量系数
num_epochs = 1000 # 训练轮次# 模型参数
w = np.random.randn() # 权重初始化
b = np.random.randn() # 偏差初始化# 动量变量初始化
v_w = 0
v_b = 0# 训练数据(示例)
X = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 5, 7, 11])# 训练过程
for epoch in range(num_epochs):# 计算预测值y_pred = w * X + b# 计算损失loss = np.mean((y - y_pred) ** 2)# 计算梯度grad_w = -2 * np.mean((y - y_pred) * X)grad_b = -2 * np.mean(y - y_pred)# 更新动量v_w = beta * v_w + (1 - beta) * grad_wv_b = beta * v_b + (1 - beta) * grad_b# 更新参数w -= alpha * v_wb -= alpha * v_bif epoch % 100 == 0:print(f"Epoch {epoch}, Loss: {loss}, w: {w}, b: {b}")print(f"Final parameters: w: {w}, b: {b}")
4. 结果分析
通过上述代码,我们定义了一个简单的线性回归模型,在训练过程中应用动量法以进行参数更新。需要注意的是,我们在每个轮次中计算损失以及参数,通过调整学习率和动量系数,从而观察到模型如何逐步收敛。
在使用动量法后,我们会发现与普通SGD相比,损失下降得更快,参数更新更加平滑,最终得到的模型效果更好。
总结
动量法是优化算法中一个极其重要的概念,它通过对历史梯度的加权平均来稳定参数更新过程,提高收敛速度。通过引入动量,我们能够在训练过程中减少震荡,快速逃离局部最优,达到更好的收敛效果。
本文对动量法的原理、公式以及实践应用进行了详细的介绍,期望能够为你在深度学习的道路上提供有益的帮助。希望在未来的学习中,大家能够深入掌握动量法及其变种,为构建更为复杂和精确的模型奠定基础。
相关文章:

AI学习指南深度学习篇-带动量的随机梯度下降法的基本原理
AI学习指南深度学习篇——带动量的随机梯度下降法的基本原理 引言 在深度学习中,优化算法被广泛应用于训练神经网络模型。随机梯度下降法(SGD)是最常用的优化算法之一,但单独使用SGD在收敛速度和稳定性方面存在一些问题。为了应…...

点餐小程序实战教程03创建应用
目录 1 创建应用2 第一部分侧边栏3 第二部分页面功能区4 第三部分大纲树5 第四部分代码区6 第五部分模式切换7 第六部分编辑区域8 第七部分组件区域9 第八部分,发布区域10 第九部分开发调试和高阶配置总结 上一篇我们介绍了如何实现后端API,介绍了登录验…...

鸿蒙自动化发布测试版本app
创建API客户端 API客户端是AppGallery Connect用于管理用户访问AppGallery Connect API的身份凭据,您可以给不同角色创建不同的API客户端,使不同角色可以访问对应权限的AppGallery Connect API。在访问某个API前,必须创建有权访问该API的API…...

力扣9.7
115.不同的子序列 题目 给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 7 取模。 数据范围 1 < s.length, t.length < 1000s 和 t 由英文字母组成 分析 令dp[i][j]为s的前i个字符构成的子序列中为t的前j…...

GPU 带宽功耗优化
移动端GPU 的内存结构: 先简述移动端内存cache结构;上图的UMA结构 on-Chip memory 包括了 L1、L2 cache,非常关键的移动端的 Tiles 也是保存在 on-chip上还包括寄存器文件:提供给每个核心使用的极高速存储。 共享内存(…...

Linux Centos 7网络配置
本步骤基于Centos 7,使用的虚拟机是VMware Workstation Pro,最终可实现虚拟机与外网互通。如为其他发行版本的linux,可能会有差异。 1、检查外网访问状态 ping www.baidu.com 2、查看网卡配置信息 ip addr 3、配置网卡 cd /etc/sysconfig…...

第三天旅游线路规划
第三天:从贾登峪到禾木风景区,晚上住宿贾登峪; 从贾登峪到禾木风景区入口: 1、行程安排 根据上面的耗时情况,规划一天的行程安排如下: 1)早上9:00起床,吃完早饭&#…...

C++第四十七弹---深入理解异常机制:try, catch, throw全面解析
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】 目录 1.C语言传统的处理错误的方式 2.C异常概念 3. 异常的使用 3.1 异常的抛出和捕获 3.2 异常的重新抛出 3.3 异常安全 3.4 异常规范 4.自定义…...

go 和 java 技术选型思考
背景: go和java我这边自身都在使用,感受比较深,java使用了有7年多,go也就是今年开始的,公司需要所以就学了使用,发现这两个语言都很好,需要根据场景选择,我写下我这边的看法。 关于…...

传统CV算法——边缘算子与图像金字塔算法介绍
边缘算子 图像梯度算子 - Sobel Sobel算子是一种用于边缘检测的图像梯度算子,它通过计算图像亮度的空间梯度来突出显示图像中的边缘。Sobel算子主要识别图像中亮度变化快的区域,这些区域通常对应于边缘。它是通过对图像进行水平和垂直方向的差分运算来…...

图像去噪算法性能比较与分析
在数字图像处理领域,去噪是一个重要且常见的任务。本文将介绍一种实验,通过MATLAB实现多种去噪算法,并比较它们的性能。实验中使用了包括中值滤波(MF)、自适应加权中值滤波(ACWMF)、差分同态算法…...
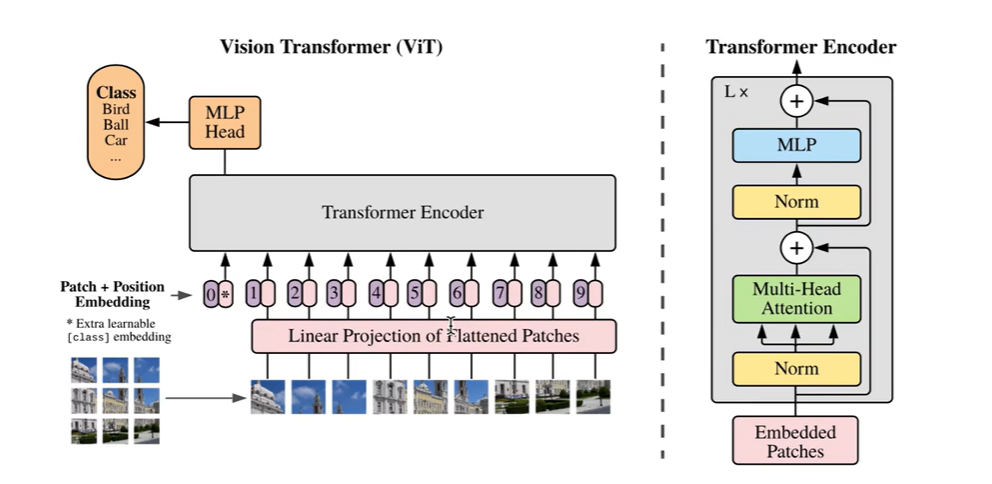
Vision Transformer(ViT)模型原理及PyTorch逐行实现
Vision Transformer(ViT)模型原理及PyTorch逐行实现 一、TRM模型结构 1.Encoder Position Embedding 注入位置信息Multi-head Self-attention 对各个位置的embedding融合(空间融合)LayerNorm & ResidualFeedforward Neural Network 对每个位置上单…...

828华为云征文 | Flexus X实例CPU、内存及磁盘性能实测与分析
引言 随着云计算的普及,企业对于云资源的需求日益增加,而选择一款性能强劲、稳定性高的云实例成为了关键。华为云Flexus X实例作为华为云最新推出的高性能实例,旨在为用户提供更强的计算能力和更高的网络带宽支持。最近华为云828 B2B企业节正…...
队列)
FreeRTOS学习笔记(六)队列
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、队列的基本内容1.1 队列的引入1.2 FreeRTOS 队列的功能与作用1.3 队列的结构体1.4 队列的使用流程 二、相关API详解2.1 xQueueCreate2.2 xQueueSend2.3 xQu…...

【Python篇】PyQt5 超详细教程——由入门到精通(中篇一)
文章目录 PyQt5入门级超详细教程前言第4部分:事件处理与信号槽机制4.1 什么是信号与槽?4.2 信号与槽的基本用法4.3 信号与槽的基础示例代码详解: 4.4 处理不同的信号代码详解: 4.5 自定义信号与槽代码详解: 4.6 信号槽…...

LinuxQt下的一些坑之一
我们在使用Qt开发时,经常会遇到Windows上应用正常,但到Linux嵌入式下就会出现莫名奇妙的问题。这篇文章就举例分析下: 1.QPushButton按钮外侧虚线框问题 Windows下QPushButton按钮设置样式正常,但到了Linux下就会有一个虚线边框。…...

Statement batch
我们可以看到 Statement 和 PreparedStatement 为我们提供的批次执行 sql 操作 JDBC 引入上述 batch 功能的主要目的,是加快对客户端SQL的执行和响应速度,并进而提高数据库整体并发度,而 jdbc batch 能够提高对客户端SQL的执行和响应速度,其…...

PPP 、PPPoE 浅析和配置示例
一、名词: PPP: Point to Point Protocol 点到点协议 LCP:Link Control Protocol 链路控制协议 NCP:Network Control Protocol 网络控制协议,对于上层协议的支持,N 可以为IPv4、IPv6…...

【Python机器学习】词向量推理——词向量
目录 面向向量的推理 使用词向量的更多原因 如何计算Word2vec表示 skip-gram方法 什么是softmax 神经网络如何学习向量表示 用线性代数检索词向量 连续词袋方法 skip-gram和CBOW:什么时候用哪种方法 word2vec计算技巧 高频2-gram 高频词条降采样 负采样…...
)
Python 语法糖:让编程更简单(续二)
Python 语法糖:让编程更简单(续) 10. Type hints Type hints 是 Python 中的一种语法糖,用于指定函数或变量的类型。例如: def greet(name: str) -> None:print(f"Hello, {name}!")这段代码将定义一个…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
