李宏毅机器学习笔记——反向传播算法
反向传播算法
反向传播(Backpropagation)是一种用于训练人工神经网络的算法,它通过计算损失函数相对于网络中每个参数的梯度来更新这些参数,从而最小化损失函数。反向传播是深度学习中最重要的算法之一,通常与梯度下降等优化算法结合使用。
反向传播的基本原理
反向传播的核心思想是利用链式法则(Chain Rule)来高效地计算损失函数相对于每个参数的梯度。以下是反向传播的基本步骤:
-
前向传播(Forward Pass):
- 输入数据通过神经网络进行传播,计算出每一层的输出,直到得到最终的预测结果。
- 计算损失函数,评估预测结果与真实标签之间的差异。
-
计算损失函数的梯度:
- 从输出层开始,计算损失函数相对于输出的梯度。
- 通过链式法则,将梯度逐层向后传播,计算每一层的梯度。
-
更新参数:
- 使用计算得到的梯度更新网络中的权重和偏置,通常使用梯度下降法或其变种(如 Adam、RMSprop 等)。
反向传播的数学细节
假设我们有一个简单的神经网络,包含输入层、隐藏层和输出层。设定损失函数为 L L L,网络的参数为 W W W 和 b b b(权重和偏置),反向传播的步骤如下:
-
前向传播:
- 计算输出:
y pred = f ( W ⋅ x + b ) y_{\text{pred}} = f(W \cdot x + b) ypred=f(W⋅x+b) - 计算损失:
L = Loss ( y true , y pred ) L = \text{Loss}(y_{\text{true}}, y_{\text{pred}}) L=Loss(ytrue,ypred)
- 计算输出:
-
反向传播:
- 计算输出层的梯度:
∂ L ∂ y pred \frac{\partial L}{\partial y_{\text{pred}}} ∂ypred∂L - 计算隐藏层的梯度:
∂ L ∂ W = ∂ L ∂ y pred ⋅ ∂ y pred ∂ W \frac{\partial L}{\partial W} = \frac{\partial L}{\partial y_{\text{pred}}} \cdot \frac{\partial y_{\text{pred}}}{\partial W} ∂W∂L=∂ypred∂L⋅∂W∂ypred - 继续向前传播,直到输入层。
- 计算输出层的梯度:
-
更新参数:
- 使用学习率 η \eta η 更新参数:
W = W − η ⋅ ∂ L ∂ W W = W - \eta \cdot \frac{\partial L}{\partial W} W=W−η⋅∂W∂L
b = b − η ⋅ ∂ L ∂ b b = b - \eta \cdot \frac{\partial L}{\partial b} b=b−η⋅∂b∂L
- 使用学习率 η \eta η 更新参数:
反向传播的优点
- 高效性:反向传播算法通过链式法则高效地计算梯度,避免了对每个参数单独计算梯度的高昂成本。
- 适应性:可以应用于各种类型的神经网络,包括全连接网络、卷积神经网络(CNN)、递归神经网络(RNN)等。
反向传播是训练神经网络的核心算法,通过计算损失函数的梯度并更新网络参数,使得模型能够逐步提高预测的准确性。它是深度学习的基础,使得复杂的神经网络能够有效地学习和优化。
链式法则
- 反向传播算法是一种利用链式法则计算微分的算法。
- 在一维的情况下,链式法则为: d z d x = d z d y × d y d x \frac{d z}{d x}=\frac{d z}{d y} \times \frac{d y}{d x} dxdz=dydz×dxdy 。
- 在多维情况下,设: x → ∈ R m , y → ∈ R n , g \overrightarrow{\mathbf{x}} \in \mathbb{R}^{m}, \overrightarrow{\mathbf{y}} \in \mathbb{R}^{n} , g x∈Rm,y∈Rn,g 为 R m \mathbb{R}^{m} Rm 到 R n \mathbb{R}^{n} Rn 的映射且满足 y → = g ( x → ) , f \overrightarrow{\mathbf{y}}=g(\overrightarrow{\mathbf{x}}) , f y=g(x),f 为 R n \mathbb{R}^{n} Rn 到 R \mathbb{R} R 的映射且满 足 z = f ( y → ) z=f(\overrightarrow{\mathbf{y}}) z=f(y) 。则有:
∂ z ∂ x i = ∑ j = 1 n ∂ z ∂ y j ∂ y j ∂ x i , i = 1 , 2 , ⋯ , m \frac{\partial z}{\partial x_{i}}=\sum_{j=1}^{n} \frac{\partial z}{\partial y_{j}} \frac{\partial y_{j}}{\partial x_{i}}, \quad i=1,2, \cdots, m ∂xi∂z=j=1∑n∂yj∂z∂xi∂yj,i=1,2,⋯,m
使用向量记法,可以等价地写作:
∇ x → z = ( ∂ y → ∂ x → ) T ∇ y → z \nabla_{\overrightarrow{\mathbf{x}}} z=\left(\frac{\partial \overrightarrow{\mathbf{y}}}{\partial \overrightarrow{\mathbf{x}}}\right)^{T} \nabla_{\overrightarrow{\mathbf{y}} z} ∇xz=(∂x∂y)T∇yz
其中: ∂ y → ∂ x → \frac{\partial \overrightarrow{\mathbf{y}}}{\partial \overrightarrow{\mathbf{x}}} ∂x∂y 为 g g g 的 n × m n \times m n×m 阶雅可比矩阵, ∇ x → z \nabla_{\overrightarrow{\mathbf{x}}} z ∇xz 为 z z z 对 x → \overrightarrow{\mathbf{x}} x 的梯度, ∇ y → z \nabla_{\overrightarrow{\mathbf{y}}} z ∇yz 为 z z z 对 y → \overrightarrow{\mathbf{y}} y 的梯度:
∇ x → z = [ ∂ z ∂ x 1 ∂ z ∂ x 2 ⋮ ∂ z ∂ x m ] ∇ y → z = [ ∂ z ∂ y 1 ∂ z ∂ y 2 ⋮ ∂ z ∂ y n ] ∂ y → ∂ x → = [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 ⋯ ∂ y 1 ∂ x n s ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 ⋯ ∂ y 2 ∂ x m ⋮ ⋮ ⋱ ⋮ ∂ y n ∂ x 1 ∂ y n ∂ x 2 ⋯ ∂ y n ∂ x m ] \nabla_{\overrightarrow{\mathbf{x}}} z=\left[\begin{array}{c} \frac{\partial z}{\partial x_{1}} \\ \frac{\partial z}{\partial x_{2}} \\ \vdots \\ \frac{\partial z}{\partial x_{m}} \end{array}\right] \quad \nabla_{\overrightarrow{\mathbf{y}}} z=\left[\begin{array}{c} \frac{\partial z}{\partial y_{1}} \\ \frac{\partial z}{\partial y_{2}} \\ \vdots \\ \frac{\partial z}{\partial y_{n}} \end{array}\right] \quad \frac{\partial \overrightarrow{\mathbf{y}}}{\partial \overrightarrow{\mathbf{x}}}=\left[\begin{array}{cccc} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} & \cdots & \frac{\partial y_{1}}{\partial x_{n s}} \\ \frac{\partial y_{2}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{2}} & \cdots & \frac{\partial y_{2}}{\partial x_{m}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_{n}}{\partial x_{1}} & \frac{\partial y_{n}}{\partial x_{2}} & \cdots & \frac{\partial y_{n}}{\partial x_{m}} \end{array}\right] ∇xz= ∂x1∂z∂x2∂z⋮∂xm∂z ∇yz= ∂y1∂z∂y2∂z⋮∂yn∂z ∂x∂y= ∂x1∂y1∂x1∂y2⋮∂x1∂yn∂x2∂y1∂x2∂y2⋮∂x2∂yn⋯⋯⋱⋯∂xns∂y1∂xm∂y2⋮∂xm∂yn
张量链式法则
- 链式法则仅可以作用于向量,也可以应用于张量:
- 首先将张量展平为一维向量。
- 然后计算该向量的梯度。
- 然后将该牱度重新构造为张量。
- 记 ∇ X z \nabla_{\mathbf{X}} z ∇Xz 为 z z z 对张量 X \mathbf{X} X 的梯度。 X \mathbf{X} X 现在有多个索引 (如:二维张量有两个索引),可以使用单个变量 i i i 来表 示 X \mathbf{X} X 的索引元组(如 i = 1 ∼ 9 i=1 \sim 9 i=1∼9 表示: 一个二维张量的系引,每个维度三个元素)。
这就与向量中的系引方式完全一致: ( ∇ X z ) i = θ z ∂ x i (\nabla \mathbf{X} z)_{i}=\frac{\theta z}{\partial x_{i}} (∇Xz)i=∂xiθz 。
奴:
X = [ x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 ] \mathbf{X}=\left[\begin{array}{lll} x_{1} & x_{2} & x_{3} \\ x_{4} & x_{5} & x_{6} \\ x_{7} & x_{8} & x_{9} \end{array}\right] X= x1x4x7x2x5x8x3x6x9
则有:
∇ X z = [ ∂ z ∂ x 1 ∂ z ∂ x 2 ∂ z ∂ x 3 ∂ z ∂ x 4 ∂ z ∂ x 5 ∂ z ∂ x 6 ∂ z ∂ x w q ∂ z ∂ z g ∂ z ∂ x 9 ] \nabla_{\mathbf{X}} z=\left[\begin{array}{ccc} \frac{\partial z}{\partial x_{1}} & \frac{\partial z}{\partial x_{2}} & \frac{\partial z}{\partial x_{3}} \\ \frac{\partial z}{\partial x_{4}} & \frac{\partial z}{\partial x_{5}} & \frac{\partial z}{\partial x_{6}} \\ \frac{\partial z}{\partial x_{w_{q}}} & \frac{\partial z}{\partial z_{g}} & \frac{\partial z}{\partial x_{9}} \end{array}\right] ∇Xz= ∂x1∂z∂x4∂z∂xwq∂z∂x2∂z∂x5∂z∂zg∂z∂x3∂z∂x6∂z∂x9∂z - 设 Y = g ( X ) , z = f ( Y ) \mathbf{Y}=g(\mathbf{X}), z=f(\mathbf{Y}) Y=g(X),z=f(Y) ,用单个变量 j j j 来表示 Y \mathbf{Y} Y 的索引元組。则张量的链式法则为:
∂ z ∂ x i = ∑ j ∂ z ∂ y j ∂ y j ∂ x i ⇒ ∇ X z = ∑ j ( ∇ X y j ) ∂ z ∂ y j \frac{\partial z}{\partial x_{i}}=\sum_{j} \frac{\partial z}{\partial y_{j}} \frac{\partial y_{j}}{\partial x_{i}} \Rightarrow \nabla_{\mathbf{X}} z=\sum_{j}\left(\nabla_{\mathbf{X}} y_{j}\right) \frac{\partial z}{\partial y_{j}} ∂xi∂z=j∑∂yj∂z∂xi∂yj⇒∇Xz=j∑(∇Xyj)∂yj∂z
如:
X = [ x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 ] \mathbf{X}=\left[\begin{array}{lll} x_{1} & x_{2} & x_{3} \\ x_{4} & x_{5} & x_{6} \\ x_{7} & x_{8} & x_{9} \end{array}\right] X= x1x4x7x2x5x8x3x6x9
则有:
∇ X z = [ ∑ j ∂ z ∂ y j ∂ y j ∂ x 1 ∑ j ∂ z ∂ y j ∂ y j ∂ x 2 ∑ j ∂ z ∂ y j ∂ y j ∂ x j ∑ j ∂ z ∂ y j ∂ y j ∂ x 4 ∑ j ∂ z ∂ y j ∂ y j ∂ x j ∑ j ∂ z ∂ y j ∂ y j ∂ x 0 ∑ j ∂ z ∂ y j ∂ y j ∂ x 7 ∑ j ∂ z ∂ y j ∂ y j ∂ x 8 ∑ j ∂ z ∂ y j ∂ y j ∂ x j ] \nabla_{\mathbf{X}} z=\left[\begin{array}{llll} \sum_{j} \frac{\partial z}{\partial y_{j}} & \frac{\partial y_{j}}{\partial x_{1}} & \sum_{j} \frac{\partial z}{\partial y_{j}} \frac{\partial y_{j}}{\partial x_{2}} & \sum_{j} \frac{\partial z}{\partial y_{j}} \frac{\partial y_{j}}{\partial x_{j}} \\ \sum_{j} \frac{\partial z}{\partial y_{j}} \frac{\partial y_{j}}{\partial x_{4}} & \sum_{j} \frac{\partial z}{\partial y_{j}} \frac{\partial y_{j}}{\partial x_{j}} & \sum_{j} \frac{\partial z}{\partial y_{j}} \frac{\partial y_{j}}{\partial x_{0}} \\ \sum_{j} \frac{\partial z}{\partial y_{j}} \frac{\partial y_{j}}{\partial x_{7}} & \sum_{j} \frac{\partial z}{\partial y_{j}} \frac{\partial y_{j}}{\partial x_{8}} & \sum_{j} \frac{\partial z}{\partial y_{j}} \frac{\partial y_{j}}{\partial x_{j}} \end{array}\right] ∇Xz= ∑j∂yj∂z∑j∂yj∂z∂x4∂yj∑j∂yj∂z∂x7∂yj∂x1∂yj∑j∂yj∂z∂xj∂yj∑j∂yj∂z∂x8∂yj∑j∂yj∂z∂x2∂yj∑j∂yj∂z∂x0∂yj∑j∂yj∂z∂xj∂yj∑j∂yj∂z∂xj∂yj
反向传播算法
- 反向传播算法:
- 输入:
- 计算图 G \mathcal{G} G
- 初始化参数向量 u ⃗ ∗ \vec{u}^{*} u∗
。 输出: ∂ u n ∂ u j , j = 1 , 2 , ⋯ , n i \frac{\partial u_{n}}{\partial u_{j}}, j=1,2, \cdots, n_{i} ∂uj∂un,j=1,2,⋯,ni - 运行计算 u n u_{n} un 的前向算法,获取每个节点的值。
- 给出一个 grad_table 表,它存储的是已经计算出来的偏导数。
u i u_{i} ui 对应的表项存储的是偏导数 ∂ u n ∂ u i \frac{\partial u_{n}}{\partial u_{i}} ∂ui∂un 。 - 初始化 grad_table [ u n ] = 1 \left[u_{n}\right]=1 [un]=1 。
- 沿着计算图 B \mathcal{B} B 计算偏导数。遍历 j j j 从 n − 1 n-1 n−1 到 1 :
- 计算 ∂ u u n ∂ u j = ∑ u i ∈ C j ∂ u n ∂ u i ∂ u i ∂ u j \frac{\partial u_{u_{n}}}{\partial u_{j}}=\sum_{u_{i} \in \mathbb{C}_{j}} \frac{\partial u_{n}}{\partial u_{i}} \frac{\partial u_{i}}{\partial u_{j}} ∂uj∂uun=∑ui∈Cj∂ui∂un∂uj∂ui 。其中: ∂ u n ∂ u i \frac{\partial u_{n}}{\partial u_{i}} ∂ui∂un 是已经存储的 grad_table[ui ] ] ], ∂ u i ∂ u j \frac{\partial u_{i}}{\partial u_{j}} ∂uj∂ui 为实时计算的。
图 G \mathcal{G} G 中的边 u j → u i u_{j} \rightarrow u_{i} uj→ui 定义了一个操作,而该操作的偏导只依赖于这两个变量,因此可以实时求 解 ∂ u i ∂ u j \frac{\partial u_{i}}{\partial u_{j}} ∂uj∂ui 。 - 存储 grad \operatorname{grad} grad _able [ u j ] 。 \left[u_{j}\right]_{\text {。 }} [uj]。
- 逅回 grad table [ u j ] , j = 1 , 2 , ⋯ , n j ^ \operatorname{grad} \operatorname{table}\left[u_{j}\right], j=1,2, \cdots, n_{\hat{j}} gradtable[uj],j=1,2,⋯,nj^ 。
- 反向传播算法计算所有的偏导数,计算量与 G \mathcal{G} G 中的边的数量成正比。
其中每条边的计算包括计算偏导数,以及执行一次向量点积。 - 上述反向传播算法为了减少公共子表达式的计算量,并没有考虑存储的开销。这避免了重复子表达式的指数 级的增长。
。 某些算法可以通过对计算图进行简化从而避免更多的子表达式。
。 有些算法会重新认算这些子表达式而不是存储它们,从而节省内存。
参考
DataWhale
http://www.huaxiaozhuan.com/
相关文章:

李宏毅机器学习笔记——反向传播算法
反向传播算法 反向传播(Backpropagation)是一种用于训练人工神经网络的算法,它通过计算损失函数相对于网络中每个参数的梯度来更新这些参数,从而最小化损失函数。反向传播是深度学习中最重要的算法之一,通常与梯度下降…...

内推|京东|后端开发|运维|算法...|北京 更多岗位扫内推码了解,直接投递,跟踪进度
热招岗位 更多岗位欢迎扫描末尾二维码,小程序直接提交简历等面试。实时帮你查询面试进程。 安全运营中心研发工程师 岗位要求 1、本科及以上学历,3年以上的安全相关工作经验; 2、熟悉c/c、go编程语言之一、熟悉linux网络编程和系统编程 3、…...

编写Dockerfile第二版
目标 更快的构建速度 更小的Docker镜像大小 更少的Docker镜像层 充分利用镜像缓存 增加Dockerfile可读性 让Docker容器使用起来更简单 总结 编写.dockerignore文件 容器只运行单个应用 将多个RUN指令合并为一个 基础镜像的标签不要用latest 每个RUN指令后删除多余文…...

校验码:奇偶校验,CRC循环冗余校验,海明校验码
文章目录 奇偶校验码CRC循环冗余校验码海明校验码 奇偶校验码 码距:任何一种编码都由许多码字构成,任意两个码字之间最少变化的二进制位数就称为数据检验码的码距。 奇偶校验码的编码方法是:由若干位有效信息(如一个字节),再加上…...

增维思考,减维问题,避免焦虑!
什么是嵌入式软件开发的核心技能? 1. 编程语言 熟练掌握C/C:C语言是嵌入式领域最重要也是最主要的编程语言,用于实现系统功能和性能优化。C在需要面向对象编程的场合也是重要的选择。了解汇编语言:在某些需要直接与硬件交互或优…...

自动化抢票 12306
自动化抢票 12306 1. 明确需求 明确采集的网站以及数据内容 网址: https://kyfw.12306.cn/otn/leftTicket/init数据: 车次相关信息 2. 抓包分析 通过浏览器开发者工具分析对应的数据位置 打开开发者工具 F12 或鼠标右键点击检查 刷新网页 点击下一页/下滑网页页面/点击搜…...

海外云服务器安装 MariaDB10.6.X (Ubuntu 18.04 记录篇二)
本文首发于 秋码记录 MariaDB 的由来(历史) 谈起新秀MariaDB,或许很多人都会感到陌生吧,但若聊起享誉开源界、业界知名的关系型数据库——Mysql,想必混迹于互联网的人们(coder)无不知晓。 其…...

Mybatis_基础
文章目录 第一章 Mybatis简介1.1 Mybatis特性1.2 和其它持久化层技术对比 第二章 Mybatis的增删改查第三章 Mybatis的增删改查 第一章 Mybatis简介 1.1 Mybatis特性 MyBatis 是支持定制化 SQL、存储过程以及高级映射的优秀的持久层框架。MyBatis 避免了几乎所有的 JDBC 代码和…...

8Manage采购申请管理:轻松实现手动采购流程自动化
您是否感受到通过手动采购申请流程管理成本的压力? 信息的不充分常常导致现金流的不透明,这已成为财务高管们的常见痛点。本文将展示采购申请管理软件如何帮助您减轻负担,使您能够简化流程。 没有采购申请软件会面临哪些挑战? …...

PADS Router 入门基础教程(一)
有将近三周没有更新过博客了,最近在整理PADS Router 入门基础教程,希望喜欢本系列教程的小伙伴可以点点关注和订阅!下面我们开始进入PADS Router课程的介绍。 一、PADS Router 快捷键 二、课程介绍 本教程主要介绍:PADS Rou…...

一台手机一个ip地址吗?手机ip地址泄露了怎么办
在数字化时代,手机作为我们日常生活中不可或缺的一部分,其网络安全性也日益受到关注。其中一个常见的疑问便是:“一台手机是否对应一个固定的IP地址?”实际上,情况并非如此简单。本文首先解答这一问题&a…...

【扇贝编程】使用Selenium模拟浏览器获取动态内容笔记
文章目录 selenium安装 selenium下载浏览器驱动 获取数据处理数据查找一个元素查找所有符合条件的元素 控制浏览器 selenium selenium是爬虫的好帮手, 可以控制你的浏览器,模仿人浏览网页,从而获取数据,自动操作等。 我们只要让…...

TCP Analysis Flags 之 TCP Port numbers reused
前言 默认情况下,Wireshark 的 TCP 解析器会跟踪每个 TCP 会话的状态,并在检测到问题或潜在问题时提供额外的信息。在第一次打开捕获文件时,会对每个 TCP 数据包进行一次分析,数据包按照它们在数据包列表中出现的顺序进行处理。可…...

【Python机器学习】核心数、进程、线程、超线程、L1、L2、L3级缓存
如何知道自己电脑的CPU是几核的,打开任务管理器(同时按下:Esc键、SHIFT键、CTRL键) 然后,点击任务管理器左上角的性能选项,观察右下角中的内核:后面的数字,就是你CPU的核心数,下图中我的是16个核心的。 需要注意的是,下面的逻辑处理器:32 表示支持 32 线程(即超线…...

JavaScript使用地理位置 API
前言 在JavaScript中,Geolocation API 是一种用于访问用户地理位置的接口。这个API允许网页应用程序获取用户的位置并提供基于位置的服务。 if (navigator.geolocation)navigator.geolocation.getCurrentPosition(function () {},function () {});这个函数中需要传…...

dockerfile部署fastapi项目
dockerfile部署fastapi项目 1、Dockerfile # 使用Python官方镜像作为基础镜像 FROM python:3.8-slim# 更新apt-get源并安装依赖 # RUN apt-get update -y && apt-get install -y git# 设置环境变量 ENV PYTHONDONTWRITEBYTECODE 1 ENV PYTHONUNBUFFERED 1# 创建工作目…...
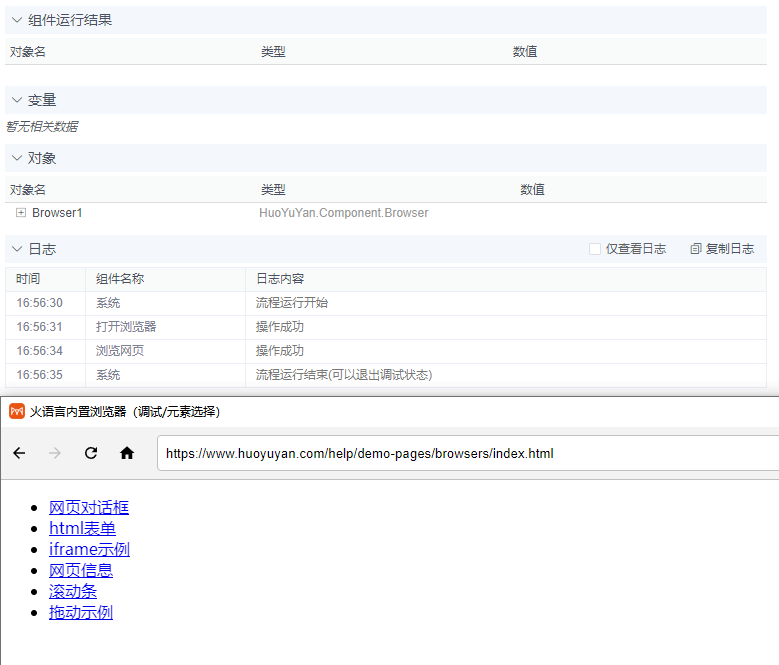
火语言RPA流程组件介绍--浏览网页
🚩【组件功能】:浏览器打开指定网址或本地html文件 配置预览 配置说明 网址URL 支持T或# 默认FLOW输入项 输入需要打开的网址URL 超时时间 支持T或# 打开网页超时时间 执行后后等待时间(ms) 支持T或# 当前组件执行完成后继续等待的时间 UserAgen…...

【Linux系统学习】2.Linux基础命令
Linux基础命令 Linux的目录结构 Linux命令入门 目录切换相关命令(cd/pwd) 相对路径、绝对路径和特殊路径符 创建目录命令(mkdir) 文件操作命令part1(touch、cat、more) 文件操作命令part2(cp、mv、rm) 查找命令(which、find) grep、wc和管道符…...

ABAP正则表达式 特殊字符处理
REPLACE ALL OCCURRENCES OF REGEX [[:space:]] IN <fs_purhdinfo>-cell_value WITH ."可去掉空格或回车键 REPLACE ALL OCCURRENCES OF : IN <fs_purhdinfo>-cell_value WITH ."可去掉空格或回车键 REPLACE ALL OCCURRENCES OF R…...

【2024高教社杯全国大学生数学建模竞赛】ABCDEF题 问题分析、模型建立、参考文献及实现代码
【2024高教社杯全国大学生数学建模竞赛】ABCDEF题 问题分析、模型建立、参考文献及实现代码 1 比赛时间 北京时间:2024年9月5日 18:00-2024年9月8日20:00 2 思路内容 2.1 往届比赛资料 【2022高教社杯数学建模】C题:古代玻璃制品的成分分析与鉴别方案…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
