2024第三届大学生算法大赛 真题训练一 解题报告 | 珂学家
前言

题解
这是第三届大学生算法大赛(第二届为清华社杯)的赛前练习赛一.
这是上界比赛的体验报告: 2023第二届“清华社杯”大学生算法大赛 解题报告(流水账版) | 珂学家,个人还是非常推荐这个比赛。
难度分布:4 easy/4 mid-hard/2 hard
赛前练习赛一,出自题库的每日一题,相对比较简单,又特别偏数学题。
所以这个练习赛一,感觉代表性不是那么强,但是又能代表官方的一种出题倾向吧。

A. 区间内的真素数

思路:质数筛/质数判定
因为数据范围不是很大,所以两类思路都可以
用欧拉筛的时候,需要注意范围(翻转会变大)
区间筛也可以试试
#include <bits/stdc++.h>using namespace std;const int SZ = (int)1e6;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int l, r;cin >> l >> r;// 欧拉筛vector<int> primes;vector<bool> vis(SZ + 1, true);vis[0] = vis[1] = false;for (int i = 2; i <= SZ; i++) {if (vis[i]) {primes.push_back(i);}for (int v: primes) {if (i > SZ / v) break;vis[i * v] = false;if (i % v == 0) break;}}function<bool(int)> checker = [&](int v) {int rv = 0;while (v > 0) {int r = v % 10;rv = rv * 10 + r;v /= 10;}return vis[rv];};vector<int> res;for (int v: primes) {if (v >= l && v <= r) {if (checker(v)) {res.push_back(v);}} else if (v > r) {break;}}if (res.empty()) {cout << "No" << '\n';} else {for (int i = 0; i < res.size(); i++) {cout << res[i] << ",\n"[i == res.size() - 1];}}return 0;
}B. 开关灯2

思路:调和级数/欧拉函数
属于思维题,但是背后还是数学
有两种思路
- 调和级数
其复杂度为 n l o g n nlogn nlogn
- 欧拉函数
就是求某个数的因子个数
x = ∏ a i p i = > p h i ( x ) = ∏ ( p i + 1 ) x = \prod a_i^{p_i} => phi(x)=\prod (p_i+1) x=∏aipi=>phi(x)=∏(pi+1)
这边采用调和级数做法
#include <bits/stdc++.h>using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int n;cin >> n;// 调和级数 nlognvector<int> arr(n + 1, 1);for (int i = 1; i <= n; i++) {for (int j = i; j <= n; j+=i) {arr[j] ^= 1;}}bool flag = false;for (int i = 1; i <= n; i++) {if (arr[i] == 0) {if (flag) cout << " ";cout << i;flag = true;}}cout << '\n';return 0;
}C. 判断一个数能否同时被3和5整除

题型:签到题
#include <bits/stdc++.h>using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int n;cin >> n;cout << ((n % 15 == 0) ? "Yes" : "No") << '\n';return 0;
}
D. 月份有几天

题型:模拟+签到
#include <bits/stdc++.h>using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int y, m;cin >> y >> m;function<bool(int)> isYean = [](int y) {return (y % 4 == 0 && y % 100 != 0) || (y % 400 == 0);};int days[2][12] = {{31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31},{31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31},};if (isYean(y)) {cout << days[1][m - 1] << endl;} else {cout << days[0][m - 1] << endl;}return 0;
}
E. 数字反转

题型:签到
保证不存在 -0这样的数据存在
#include <bits/stdc++.h>using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int n;cin >> n;int rn = 0;int sign = 1;if (n < 0) {sign = -1;n = -n;}while (n > 0) {rn = rn * 10 + (n % 10);n /= 10;}cout << sign * rn << endl;return 0;
}
写在最后

相关文章:

2024第三届大学生算法大赛 真题训练一 解题报告 | 珂学家
前言 题解 这是第三届大学生算法大赛(第二届为清华社杯)的赛前练习赛一. 这是上界比赛的体验报告: 2023第二届“清华社杯”大学生算法大赛 解题报告(流水账版) | 珂学家,个人还是非常推荐这个比赛。 难度分布:4 easy/4 mid-hard/2 hard 赛前练习赛一…...

IIS网站允许3D模型类型的文件
参与threejs项目的研发,本地开发完成后,发布后使用时发现模型文件不能正常获取资源,原因是IIS站点默认不支持模型类型。 一开始是通过直接在IIS网站管理中的类型添加来实现网站对类型的支持。 后来发现一段对于后端来说可以直接实现代码上添加…...

Linux 性能调优之CPU上下文切换
写在前面 博文内容为 Linux 性能指标 CPU 上下文切换认知内容涉及: 上下文认知,发生上下文切换的场景有哪些上下文指标信息查看,内核上下文切换事件跟踪,系统上下文切换统计上下文异常场景分析,CPU亲和性配置优化上下文…...

【无标题】符文价值的退化页
我们利用现有的符文体系建立了一个健全的符文扩展空间,可假若符文让我们感到十分困惑,我们不介意毁灭它们,让一切回到没有字迹的蛮荒纪。 如此,眼睛也失去了作用。我们的成GUO也会给后来者提供又是一DUI 令人眼花缭乱的无用符咒。…...

DFS 算法:洛谷B3625迷宫寻路
我的个人主页 {\large \mathsf{{\color{Red} 我的个人主页} } } 我的个人主页 往 {\color{Red} {\Huge 往} } 往 期 {\color{Green} {\Huge 期} } 期 文 {\color{Blue} {\Huge 文} } 文 章 {\color{Orange} {\Huge 章}} 章 DFS 算法:记忆化搜索DFS 算法…...

结构开发笔记(七):solidworks软件(六):装配摄像头、摄像头座以及螺丝,完成摄像头结构示意图
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/141931518 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...

Android 15 新特性快速解读指南
核心要点 16K 页面大小支持目前作为开发人员选项提供,并非强制要求。 引入多项提升开发体验、多语言支持、多媒体功能、交互体验和隐私安全的更新。 重点关注前台服务限制、Window Insets 行为变化、AndroidManifest 文件限制等适配要求。 开发体验 ApplicationS…...
】机器人工具箱Link类函数参数说明)
【机器人工具箱Robotics Toolbox开发笔记(十九)】机器人工具箱Link类函数参数说明
机器人工具箱中的Link对象保存于机器人连杆相关的所有信息,如运动学参数、刚体惯性参数、电机和传动参数等。 与Link对象有关参数如表1所示。 表1 Link对象参数 参 数 意 义 参 数 意 义 A 连杆变换矩阵 islimit 测试关节是否超过软限制 RP RP关节类型 isrevo…...

排查SQL Server中的内存不足及其他疑难问题
文章目录 引言I DMV 资源信号灯资源信号灯 DMV sys.dm_exec_query_resource_semaphores( 确定查询执行内存的等待)查询性能计数器什么是内存授予?II DBCC MEMORYSTATUS 查询内存对象III DBCC 命令释放多个 SQL Server 内存缓存 - 临时度量值IV 等待资源池 %ls (%ld)中的内存…...
输送线相机拍照信号触发(博途PLC高速计数器中断立即输出应用)
博途PLC相关中断应用请参考下面文章链接: T法测速功能块 T法测速功能块(博途PLC上升沿中断应用)-CSDN博客文章浏览阅读165次。本文介绍了博途PLC中T法测速的原理和应用,包括如何开启上升沿中断、配置中断以及T法测速功能块的使用。重点讲述了在中断事件发生后执行的功能块处…...
)
【数学分析笔记】第3章第1节 函数极限(6)
3. 函数极限与连续函数 3.1 函数极限 【例3.1.12】 f ( x ) a n x n a n − 1 x n − 1 ⋯ a k x k b m x m b m − 1 x m − 1 ⋯ b j x j , b m , b j ≠ 0 , a n , a k ≠ 0 f(x) \frac{a_{n} x^{n}a_{n-1} x^{n-1}\cdotsa_{k} x^{k}}{b_{m} x^{m}b_{m-1} x^{m-1}\…...

程序员如何写笔记?
word。没错,我也看了网上一大堆软件,还有git管理等等。个人认为如果笔记只是记录个人的经验积累,一个word就够了,那些notepad,laTex个人觉得不够简练。word。 1.word可以插入任何文件附件(目前最大的word 200MB也没出现…...

Linux网络——Socket编程函数
一.网络命令 1.ping ping命令用来检测网络是否连通,具体用法为: ping 任意网址 结果如下: 当出现上述字段时,证明网络是连通的,这里值得注意的是,ping命令执行之后会不断进行网络检测,不会停…...
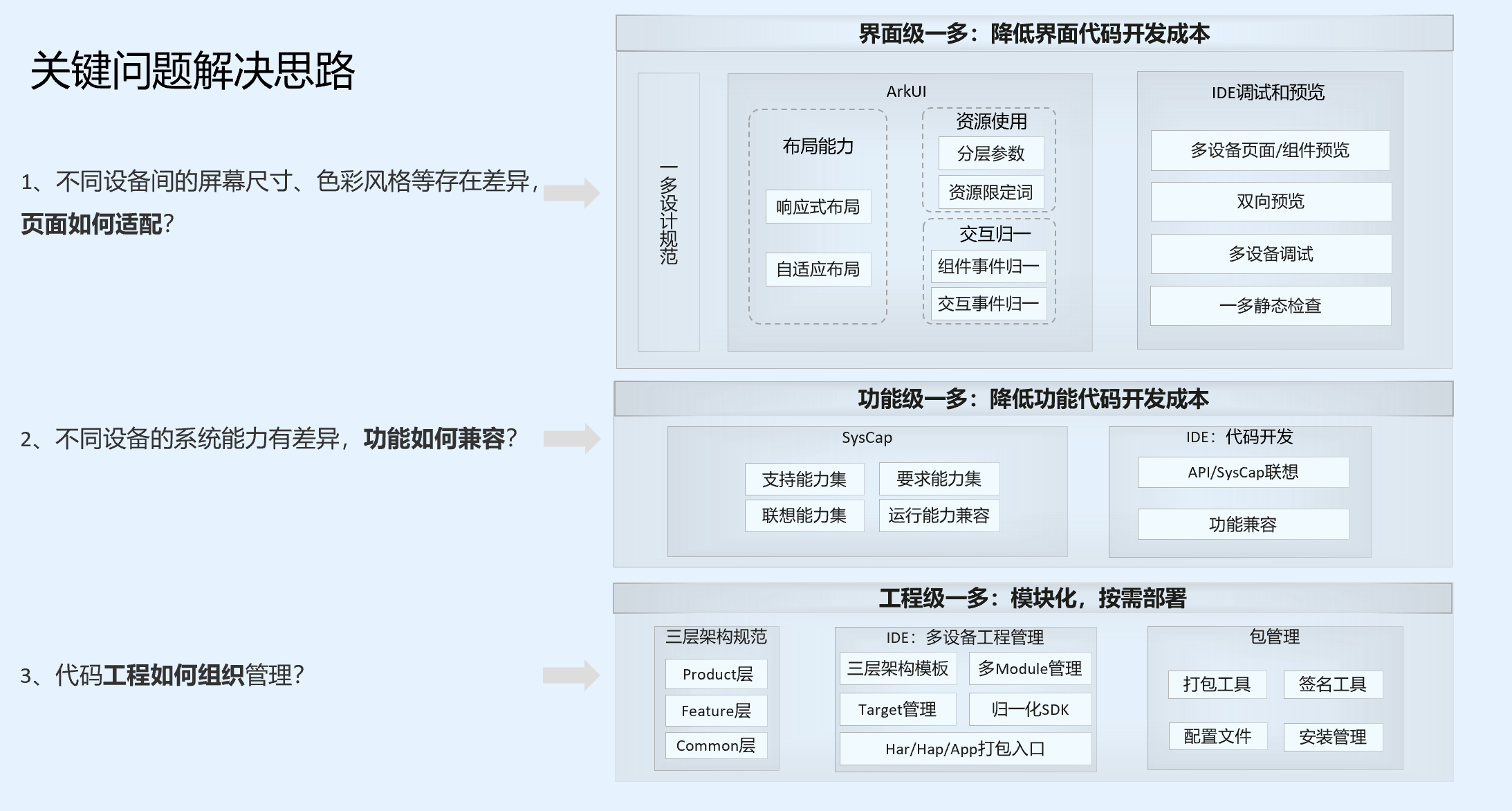
HarmonyOS 是如何实现一次开发多端部署 -- HarmonyOS自学1
一次开发多端部署遇到的几个关键问题 为了实现“一多”的目标,需要解决如下三个基础问题: 问题1:页面如何适配 不同设备间的屏幕尺寸、色彩风格等存在差异,页面如何适配。 问题2:功能如何兼容 不同设备的系统能力…...

嵌入式硬件-ARM处理器架构,CPU,SOC片上系统处理器
多进程空间内部分布图:注意:创建线程实际使用堆区空间,栈区独立 ARM处理器架构: 基于ARM920T架构的CPU:以下为哈佛结构 ALU:算数运算器 R0~R12:寄存器 PC:程序计数器,默认为0,做自加运算&#x…...

《JavaEE进阶》----12.<SpringIOCDI【扫描路径+DI详解+经典面试题+总结】>
本篇博客主要讲解 扫描路径 DI详解:三种注入方式及优缺点 经典面试题 总结 五、环境扫描路径 虽然我们没有告诉Spring扫描路径是什么,但是有一些注解已经告诉Spring扫描路径是什么了 如启动类注解SpringBootApplication。 里面有一个注解是componentS…...

Selenium 自动化测试:常用函数与实例代码
引言 Selenium 是一个强大的自动化测试工具,广泛用于网页应用的自动化测试。它支持多种编程语言,包括 Python。本文将介绍 Selenium 的常用函数,并提供参数解释和代码示例。 Selenium 简介 Selenium 是一个用于自动化 Web 应用测试的工具&…...
——爬取天气预报)
python网络爬虫(五)——爬取天气预报
1.注册高德天气key 点击高德天气,然后按照开发者文档完成key注册;作为爬虫练习项目之一。从高德地图json数据接口获取天气,可以获取某省的所有城市天气,高德地图的这个接口还能获取县城的天气。其天气查询API服务地址为https://re…...

四.海量数据实时分析-Doris数据导入导出
数据导入 1.概述 Apache Doris 提供多种数据导入方案,可以针对不同的数据源进行选择不同的数据导入方式。 数据源导入方式对象存储(s3),HDFS使用 Broker 导入数据本地文件Stream Load, MySQL LoadKafka订阅 Kafka 数据Mysql、PostgreSQL&a…...

一. 从Hive开始
1. 怎么理解Hive Hive不能理解成一个传统意义上的数据库,应该理解成一个解决方案。 是Hadoop在hdfs和mapreduce之后才出现的一个结构化数据处理的解决方案。 Hdfs解决了大数据的存储问题,mapreduce解决了数据的计算问题。 一切似乎很美好。 但是使用成本…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

Excel 怎么让透视表以正常Excel表格形式显示
目录 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总...
