【数学分析笔记】第3章第1节 函数极限(6)
3. 函数极限与连续函数
3.1 函数极限
【例3.1.12】 f ( x ) = a n x n + a n − 1 x n − 1 + ⋯ + a k x k b m x m + b m − 1 x m − 1 + ⋯ + b j x j , b m , b j ≠ 0 , a n , a k ≠ 0 f(x)= \frac{a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{k} x^{k}}{b_{m} x^{m}+b_{m-1} x^{m-1}+\cdots+b_{j} x^{j}},b_{m},b_{j}\ne 0,a_{n},a_{k}\ne 0 f(x)=bmxm+bm−1xm−1+⋯+bjxjanxn+an−1xn−1+⋯+akxk,bm,bj=0,an,ak=0,讨论极限 lim x → ∞ f ( x ) \lim\limits_{x \rightarrow \infty}f(x) x→∞limf(x)与 lim x → 0 f ( x ) \lim\limits_{x \rightarrow 0}f(x) x→0limf(x).
【解】 x → ∞ x\to\infty x→∞:
(1)若 n = m n=m n=m, lim x → ∞ f ( x ) = lim x → ∞ a n x n + a n − 1 x n − 1 + ⋯ + a k x k b m x m + b m − 1 x m − 1 + ⋯ + b j x j = lim x → ∞ a n + a n − 1 x + ⋯ + a k x n − k b n + b n − 1 x + ⋯ + b j x n − j = a n b n ; \lim\limits_{x \rightarrow \infty}f(x)=\lim\limits_{x \rightarrow \infty} \frac{a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{k} x^{k}}{b_{m} x^{m}+b_{m-1} x^{m-1}+\cdots+b_{j} x^{j}}=\lim\limits_{x \rightarrow \infty} \frac{a_{n}+\frac{a_{n-1}}{x}+\cdots+\frac{a_{k}}{x^{n-k}}}{b_{n}+\frac{b_{n-1}}{x}+\cdots+\frac{b_{j}}{x^{n-j}}}=\frac{a_{n}}{b_{n}} ; x→∞limf(x)=x→∞limbmxm+bm−1xm−1+⋯+bjxjanxn+an−1xn−1+⋯+akxk=x→∞limbn+xbn−1+⋯+xn−jbjan+xan−1+⋯+xn−kak=bnan;
(2)若 n > m n>m n>m, lim x → ∞ f ( x ) = lim x → ∞ x n ( a n + a n − 1 1 x + ⋯ + a k 1 x n − k x m ( b m + b m − 1 1 x + ⋯ + b j 1 x m − j ) = lim x → ∞ x n − m ( a n + a n − 1 1 x + ⋯ + a k 1 x n − k ( b m + b m − 1 1 x + ⋯ + b j 1 x m − j ) = ∞ \lim\limits_{x \rightarrow \infty}f(x)=\lim\limits_{x \rightarrow \infty} \frac{x^{n}(a_{n}+a_{n-1} \frac{1}{x}+\cdots+a_{k} \frac{1}{x^{n-k}}}{x^{m}(b_{m} +b_{m-1} \frac{1}{x}+\cdots+b_{j} \frac{1}{x^{m-j}})}=\lim\limits_{x \rightarrow \infty}x^{n-m} \frac{(a_{n}+a_{n-1} \frac{1}{x}+\cdots+a_{k} \frac{1}{x^{n-k}}}{(b_{m} +b_{m-1} \frac{1}{x}+\cdots+b_{j} \frac{1}{x^{m-j}})}=\infty x→∞limf(x)=x→∞limxm(bm+bm−1x1+⋯+bjxm−j1)xn(an+an−1x1+⋯+akxn−k1=x→∞limxn−m(bm+bm−1x1+⋯+bjxm−j1)(an+an−1x1+⋯+akxn−k1=∞
(3)若 n < m n<m n<m, lim x → ∞ f ( x ) = lim x → ∞ x n ( a n + a n − 1 1 x + ⋯ + a k 1 x n − k x m ( b m + b m − 1 1 x + ⋯ + b j 1 x m − j ) = lim x → ∞ x n − m ( a n + a n − 1 1 x + ⋯ + a k 1 x n − k ( b m + b m − 1 1 x + ⋯ + b j 1 x m − j ) = lim x → ∞ 1 x m − n ( a n + a n − 1 1 x + ⋯ + a k 1 x n − k ( b m + b m − 1 1 x + ⋯ + b j 1 x m − j ) = 0 \lim\limits_{x \rightarrow \infty}f(x)=\lim\limits_{x \rightarrow \infty} \frac{x^{n}(a_{n}+a_{n-1} \frac{1}{x}+\cdots+a_{k} \frac{1}{x^{n-k}}}{x^{m}(b_{m} +b_{m-1} \frac{1}{x}+\cdots+b_{j} \frac{1}{x^{m-j}})}=\lim\limits_{x \rightarrow \infty}x^{n-m} \frac{(a_{n}+a_{n-1} \frac{1}{x}+\cdots+a_{k} \frac{1}{x^{n-k}}}{(b_{m} +b_{m-1} \frac{1}{x}+\cdots+b_{j} \frac{1}{x^{m-j}})}=\lim\limits_{x \rightarrow \infty}\frac{1}{x^{m-n}} \frac{(a_{n}+a_{n-1} \frac{1}{x}+\cdots+a_{k} \frac{1}{x^{n-k}}}{(b_{m} +b_{m-1} \frac{1}{x}+\cdots+b_{j} \frac{1}{x^{m-j}})}=0 x→∞limf(x)=x→∞limxm(bm+bm−1x1+⋯+bjxm−j1)xn(an+an−1x1+⋯+akxn−k1=x→∞limxn−m(bm+bm−1x1+⋯+bjxm−j1)(an+an−1x1+⋯+akxn−k1=x→∞limxm−n1(bm+bm−1x1+⋯+bjxm−j1)(an+an−1x1+⋯+akxn−k1=0
x → 0 x\to 0 x→0:
(1)若 k = j k=j k=j, f ( x ) = a n x n + a n − 1 x n − 1 + ⋯ + a k x k b m x m + b m − 1 x m − 1 + ⋯ + b j x j = x k ( a n x n − k + a n − 1 x n − k − 1 + ⋯ + a k ) x j ( b m x m − j + b m − 1 x m − j − 1 + ⋯ + b j ) = a n x n − k + a n − 1 x n − k − 1 + ⋯ + a k b m x m − j + b m − 1 x m − j − 1 + ⋯ + b j ⇒ lim x → 0 f ( x ) = a k b j f(x)=\frac{a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{k} x^{k}}{b_{m} x^{m}+b_{m-1} x^{m-1}+\cdots+b_{j} x^{j}}=\frac{x^{k}(a_{n} x^{n-k}+a_{n-1} x^{n-k-1}+\cdots+a_{k} )}{x^{j}(b_{m} x^{m-j}+b_{m-1} x^{m-j-1}+\cdots+b_{j} )}=\frac{a_{n} x^{n-k}+a_{n-1} x^{n-k-1}+\cdots+a_{k} }{b_{m} x^{m-j}+b_{m-1} x^{m-j-1}+\cdots+b_{j} }\Rightarrow\lim\limits_{x \rightarrow 0}f(x)=\frac{a^{k}}{b^{j}} f(x)=bmxm+bm−1xm−1+⋯+bjxjanxn+an−1xn−1+⋯+akxk=xj(bmxm−j+bm−1xm−j−1+⋯+bj)xk(anxn−k+an−1xn−k−1+⋯+ak)=bmxm−j+bm−1xm−j−1+⋯+bjanxn−k+an−1xn−k−1+⋯+ak⇒x→0limf(x)=bjak;
(2)若 k > j k>j k>j, f ( x ) = a n x n + a n − 1 x n − 1 + ⋯ + a k x k b m x m + b m − 1 x m − 1 + ⋯ + b j x j = x k ( a n x n − k + a n − 1 x n − k − 1 + ⋯ + a k ) x j ( b m x m − j + b m − 1 x m − j − 1 + ⋯ + b j ) = x k − j ( a n x n − k + a n − 1 x n − k − 1 + ⋯ + a k ) ( b m x m − j + b m − 1 x m − j − 1 + ⋯ + b j ) ⇒ lim x → 0 f ( x ) = 0 f(x)=\frac{a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{k} x^{k}}{b_{m} x^{m}+b_{m-1} x^{m-1}+\cdots+b_{j} x^{j}}=\frac{x^{k}(a_{n} x^{n-k}+a_{n-1} x^{n-k-1}+\cdots+a_{k} )}{x^{j}(b_{m} x^{m-j}+b_{m-1} x^{m-j-1}+\cdots+b_{j} )}=x^{k-j}\frac{(a_{n} x^{n-k}+a_{n-1} x^{n-k-1}+\cdots+a_{k} )}{(b_{m} x^{m-j}+b_{m-1} x^{m-j-1}+\cdots+b_{j} )}\Rightarrow\lim\limits_{x \rightarrow 0}f(x)=0 f(x)=bmxm+bm−1xm−1+⋯+bjxjanxn+an−1xn−1+⋯+akxk=xj(bmxm−j+bm−1xm−j−1+⋯+bj)xk(anxn−k+an−1xn−k−1+⋯+ak)=xk−j(bmxm−j+bm−1xm−j−1+⋯+bj)(anxn−k+an−1xn−k−1+⋯+ak)⇒x→0limf(x)=0
(3)若 k < j k<j k<j, f ( x ) = a n x n + a n − 1 x n − 1 + ⋯ + a k x k b m x m + b m − 1 x m − 1 + ⋯ + b j x j = x k ( a n x n − k + a n − 1 x n − k − 1 + ⋯ + a k ) x j ( b m x m − j + b m − 1 x m − j − 1 + ⋯ + b j ) = 1 x j − k ( a n x n − k + a n − 1 x n − k − 1 + ⋯ + a k ) ( b m x m − j + b m − 1 x m − j − 1 + ⋯ + b j ) ⇒ lim x → 0 f ( x ) = ∞ f(x)=\frac{a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{k} x^{k}}{b_{m} x^{m}+b_{m-1} x^{m-1}+\cdots+b_{j} x^{j}}=\frac{x^{k}(a_{n} x^{n-k}+a_{n-1} x^{n-k-1}+\cdots+a_{k} )}{x^{j}(b_{m} x^{m-j}+b_{m-1} x^{m-j-1}+\cdots+b_{j} )}=\frac{1}{x^{j-k}}\frac{(a_{n} x^{n-k}+a_{n-1} x^{n-k-1}+\cdots+a_{k} )}{(b_{m} x^{m-j}+b_{m-1} x^{m-j-1}+\cdots+b_{j} )}\Rightarrow\lim\limits_{x \rightarrow 0}f(x)=\infty f(x)=bmxm+bm−1xm−1+⋯+bjxjanxn+an−1xn−1+⋯+akxk=xj(bmxm−j+bm−1xm−j−1+⋯+bj)xk(anxn−k+an−1xn−k−1+⋯+ak)=xj−k1(bmxm−j+bm−1xm−j−1+⋯+bj)(anxn−k+an−1xn−k−1+⋯+ak)⇒x→0limf(x)=∞
综上所述:
L = lim x → ∞ a n x n + a n − 1 x n − 1 + ⋯ + a k x k b m x m + b m − 1 x m − 1 + ⋯ + b j x j = { a n b n , n = m , 0 , n < m , ∞ , n > m ; l = lim x → 0 a n x n + a n − 1 x n − 1 + ⋯ + a k x k b m x m + b m − 1 x m − 1 + ⋯ + b j x j = { a k b k , k = j , 0 , k > j , ∞ , k < j . \begin{array}{l} L=\lim\limits_{x \rightarrow \infty} \frac{a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{k} x^{k}}{b_{m} x^{m}+b_{m-1} x^{m-1}+\cdots+b_{j} x^{j}}=\left\{\begin{array}{ll} \frac{a_{n}}{b_{n}}, & n=m, \\ 0, & n<m, \\ \infty, & n>m ; \end{array}\right. \\ l=\lim\limits_{x \rightarrow 0} \frac{a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{k} x^{k}}{b_{m} x^{m}+b_{m-1} x^{m-1}+\cdots+b_{j} x^{j}}=\left\{\begin{array}{ll} \frac{a_{k}}{b_{k}}, & k=j, \\ 0, & k>j, \\ \infty, & k<j . \end{array}\right. \end{array} L=x→∞limbmxm+bm−1xm−1+⋯+bjxjanxn+an−1xn−1+⋯+akxk=⎩ ⎨ ⎧bnan,0,∞,n=m,n<m,n>m;l=x→0limbmxm+bm−1xm−1+⋯+bjxjanxn+an−1xn−1+⋯+akxk=⎩ ⎨ ⎧bkak,0,∞,k=j,k>j,k<j.
【例3.1.13】证明 lim x → ∞ ( 1 + 1 x ) x = e \lim\limits_{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^{x}=\mathrm{e} x→∞lim(1+x1)x=e.
【证】先证 lim x → + ∞ ( 1 + 1 x ) x = e \lim\limits_{x \rightarrow+ \infty}\left(1+\frac{1}{x}\right)^{x}=\mathrm{e} x→+∞lim(1+x1)x=e, ∀ x ≥ 1 , [ x ] ≤ x < [ x ] + 1 \forall x\ge 1,[x]\le x <[x]+1 ∀x≥1,[x]≤x<[x]+1
( 1 + 1 [ x ] + 1 ) [ x ] < ( 1 + 1 x ) x < ( 1 + 1 [ x ] ) [ x ] + 1 (1+\frac{1}{[x]+1})^{[x]}<\left(1+\frac{1}{x}\right)^{x}<(1+\frac{1}{[x]})^{[x]+1} (1+[x]+11)[x]<(1+x1)x<(1+[x]1)[x]+1
由于 [ x ] [x] [x]是取整函数,则 [ x ] [x] [x]相当于数列的 n n n
lim n → ∞ ( 1 + 1 n + 1 ) n = lim n → ∞ ( 1 + 1 n + 1 ) n + 1 ⋅ 1 1 + 1 n + 1 = e \lim\limits_{n \rightarrow \infty}\left(1+\frac{1}{n+1}\right)^{n}=\lim\limits_{n \rightarrow \infty}(1+\frac{1}{n+1})^{n+1}\cdot\frac{1}{1+\frac{1}{n+1}}=\mathrm{e} n→∞lim(1+n+11)n=n→∞lim(1+n+11)n+1⋅1+n+111=e
lim n → ∞ ( 1 + 1 n ) n + 1 = lim n → ∞ ( 1 + 1 n ) n ( 1 + 1 n ) = e \lim \limits_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n+1}=\lim \limits_{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n}(1+\frac{1}{n})=\mathrm{e} n→∞lim(1+n1)n+1=n→∞lim(1+n1)n(1+n1)=e
由夹逼法可知 lim x → + ∞ ( 1 + 1 x ) x = e \lim\limits_{x \rightarrow+ \infty}\left(1+\frac{1}{x}\right)^{x}=\mathrm{e} x→+∞lim(1+x1)x=e
设 x → − ∞ x\to-\infty x→−∞,令 y = − x y=-x y=−x,则 y → + ∞ y\to+\infty y→+∞
lim x → − ∞ ( 1 + 1 x ) x = lim y → + ∞ ( 1 − 1 y ) − y = lim y → + ∞ ( y − 1 y ) − y = lim y → + ∞ ( y y − 1 ) y = lim y → + ∞ ( 1 + 1 y − 1 ) y = lim y → + ∞ ( 1 + 1 y − 1 ) y − 1 ( 1 + 1 y − 1 ) = e \lim\limits_{x \rightarrow- \infty}\left(1+\frac{1}{x}\right)^{x}=\lim\limits_{y \rightarrow+ \infty}\left(1-\frac{1}{y}\right)^{-y}=\lim\limits_{y \rightarrow+ \infty}\left(\frac{y-1}{y}\right)^{-y}=\lim\limits_{y \rightarrow+ \infty}(\frac{y}{y-1})^{y}=\lim\limits_{y \rightarrow+ \infty}(1+\frac{1}{y-1})^{y}=\lim\limits_{y \rightarrow+ \infty}(1+\frac{1}{y-1})^{y-1}(1+\frac{1}{y-1})=\mathrm{e} x→−∞lim(1+x1)x=y→+∞lim(1−y1)−y=y→+∞lim(yy−1)−y=y→+∞lim(y−1y)y=y→+∞lim(1+y−11)y=y→+∞lim(1+y−11)y−1(1+y−11)=e
综上所述 lim x → ∞ ( 1 + 1 x ) x = e \lim\limits_{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^{x}=\mathrm{e} x→∞lim(1+x1)x=e
【注】本题还能得到这个结果: lim x → ∞ ( 1 − 1 x ) x = 1 e \lim\limits_{x \rightarrow \infty}(1-\frac{1}{x})^{x}=\frac{1}{e} x→∞lim(1−x1)x=e1
3.1.5 函数极限的Cauchy(柯西)收敛原理
回忆数列极限的柯西收敛原理,数列 lim n → ∞ x n \lim\limits_{n\to\infty}x_{n} n→∞limxn收敛 ⇔ , ∀ ε > 0 , ∃ N , ∀ n , m > N : ∣ x m − x n ∣ < ε \Leftrightarrow,\forall \varepsilon>0,\exists N,\forall n,m>N:|x_{m}-x_{n}|<\varepsilon ⇔,∀ε>0,∃N,∀n,m>N:∣xm−xn∣<ε
对函数的柯西收敛原理(以 x → + ∞ x\to +\infty x→+∞为例)
lim x → + ∞ f ( x ) \lim\limits_{x\to +\infty}f(x) x→+∞limf(x)存在且有限(收敛) ⇔ ∀ ε > 0 , ∃ X , ∀ x ′ , x ′ ′ > X : ∣ f ( x ′ ) − f ( x ′ ′ ) ∣ < ε \Leftrightarrow\forall\varepsilon>0,\exists X,\forall x',x''> X:|f(x')-f(x'')|<\varepsilon ⇔∀ε>0,∃X,∀x′,x′′>X:∣f(x′)−f(x′′)∣<ε
【证】先证必要性,设 lim x → + ∞ f ( x ) = A \lim\limits_{x\to +\infty}f(x)=A x→+∞limf(x)=A,则 ∀ ε > 0 , ∃ X > 0 , ∀ x ′ , x ′ ′ > X : ∣ f ( x ′ ) − A ∣ < ε 2 , ∣ f ( x ′ ′ ) − A ∣ < ε 2 \forall \varepsilon>0,\exists X>0,\forall x',x''>X:|f(x')-A|<\frac{\varepsilon}{2},|f(x'')-A|<\frac{\varepsilon}{2} ∀ε>0,∃X>0,∀x′,x′′>X:∣f(x′)−A∣<2ε,∣f(x′′)−A∣<2ε
所以 ∣ f ( x ′ ) − f ( x ′ ′ ) ∣ = ∣ f ( x ′ ) − A + A − f ( x ′ ′ ) ∣ ≤ ∣ f ( x ′ ) − A ∣ + ∣ A − f ( x ′ ′ ) ∣ = ∣ f ( x ′ ) − A ∣ + ∣ f ( x ′ ′ ) − A ∣ < ε 2 + ε 2 = ε |f(x')-f(x'')|=|f(x')-A+A-f(x'')|\le|f(x')-A|+|A-f(x'')|=|f(x')-A|+|f(x'')-A|<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon ∣f(x′)−f(x′′)∣=∣f(x′)−A+A−f(x′′)∣≤∣f(x′)−A∣+∣A−f(x′′)∣=∣f(x′)−A∣+∣f(x′′)−A∣<2ε+2ε=ε
再证充分性, ∀ ε > 0 , ∃ X > 0 , ∀ x ′ , x ′ ′ > X : ∣ f ( x ′ ) − f ( x ′ ′ ) ∣ < ε \forall\varepsilon>0,\exists X>0,\forall x',x''>X:|f(x')-f(x'')|<\varepsilon ∀ε>0,∃X>0,∀x′,x′′>X:∣f(x′)−f(x′′)∣<ε
任取 { x n } , lim n → ∞ x n = + ∞ \{x_{n}\},\lim\limits_{n\to\infty}x_{n}=+\infty {xn},n→∞limxn=+∞,则对上述 X > 0 , ∃ N , ∀ m , n > N : x n > X , x m > X X>0, \exists N, \forall m,n>N: x_{n}>X,x_{m}>X X>0,∃N,∀m,n>N:xn>X,xm>X
则有 ∣ f ( x n ) − f ( x m ) ∣ < ε |f(x_{n})-f(x_{m})|<\varepsilon ∣f(xn)−f(xm)∣<ε
{ f ( x n ) } \{f(x_{n})\} {f(xn)}是基本数列,必定收敛
由对应的Heine(海涅)定理(任取的 { x n } \{x_{n}\} {xn})可知, lim x → + ∞ f ( x ) \lim\limits_{x\to +\infty}f(x) x→+∞limf(x)存在且有限。
今后,在建立反常积分的收敛性判别法则等方面,函数极限的Cauchy收敛原理将发挥重要的作用。
相关文章:
)
【数学分析笔记】第3章第1节 函数极限(6)
3. 函数极限与连续函数 3.1 函数极限 【例3.1.12】 f ( x ) a n x n a n − 1 x n − 1 ⋯ a k x k b m x m b m − 1 x m − 1 ⋯ b j x j , b m , b j ≠ 0 , a n , a k ≠ 0 f(x) \frac{a_{n} x^{n}a_{n-1} x^{n-1}\cdotsa_{k} x^{k}}{b_{m} x^{m}b_{m-1} x^{m-1}\…...

程序员如何写笔记?
word。没错,我也看了网上一大堆软件,还有git管理等等。个人认为如果笔记只是记录个人的经验积累,一个word就够了,那些notepad,laTex个人觉得不够简练。word。 1.word可以插入任何文件附件(目前最大的word 200MB也没出现…...

Linux网络——Socket编程函数
一.网络命令 1.ping ping命令用来检测网络是否连通,具体用法为: ping 任意网址 结果如下: 当出现上述字段时,证明网络是连通的,这里值得注意的是,ping命令执行之后会不断进行网络检测,不会停…...
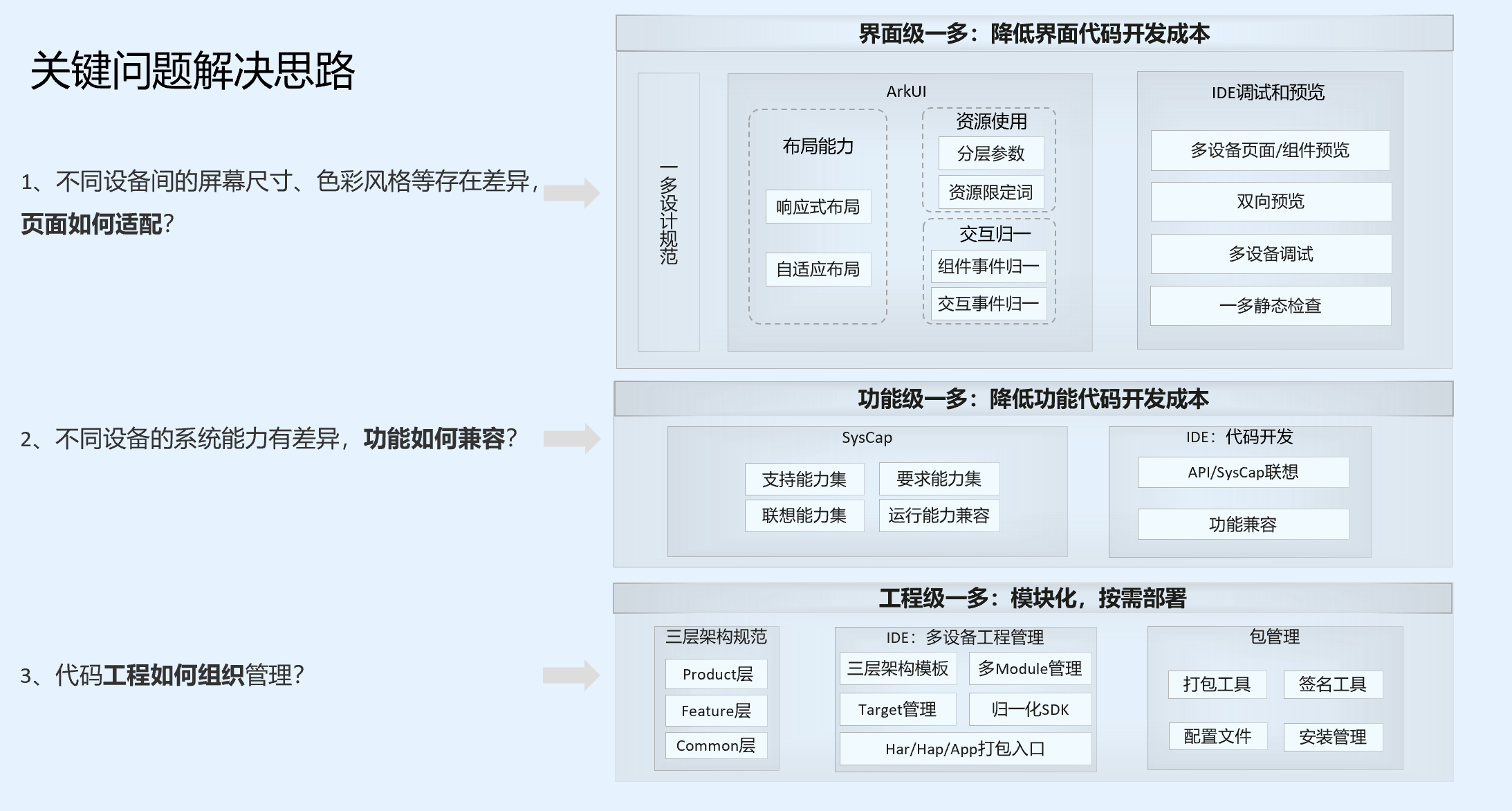
HarmonyOS 是如何实现一次开发多端部署 -- HarmonyOS自学1
一次开发多端部署遇到的几个关键问题 为了实现“一多”的目标,需要解决如下三个基础问题: 问题1:页面如何适配 不同设备间的屏幕尺寸、色彩风格等存在差异,页面如何适配。 问题2:功能如何兼容 不同设备的系统能力…...

嵌入式硬件-ARM处理器架构,CPU,SOC片上系统处理器
多进程空间内部分布图:注意:创建线程实际使用堆区空间,栈区独立 ARM处理器架构: 基于ARM920T架构的CPU:以下为哈佛结构 ALU:算数运算器 R0~R12:寄存器 PC:程序计数器,默认为0,做自加运算&#x…...

《JavaEE进阶》----12.<SpringIOCDI【扫描路径+DI详解+经典面试题+总结】>
本篇博客主要讲解 扫描路径 DI详解:三种注入方式及优缺点 经典面试题 总结 五、环境扫描路径 虽然我们没有告诉Spring扫描路径是什么,但是有一些注解已经告诉Spring扫描路径是什么了 如启动类注解SpringBootApplication。 里面有一个注解是componentS…...

Selenium 自动化测试:常用函数与实例代码
引言 Selenium 是一个强大的自动化测试工具,广泛用于网页应用的自动化测试。它支持多种编程语言,包括 Python。本文将介绍 Selenium 的常用函数,并提供参数解释和代码示例。 Selenium 简介 Selenium 是一个用于自动化 Web 应用测试的工具&…...
——爬取天气预报)
python网络爬虫(五)——爬取天气预报
1.注册高德天气key 点击高德天气,然后按照开发者文档完成key注册;作为爬虫练习项目之一。从高德地图json数据接口获取天气,可以获取某省的所有城市天气,高德地图的这个接口还能获取县城的天气。其天气查询API服务地址为https://re…...

四.海量数据实时分析-Doris数据导入导出
数据导入 1.概述 Apache Doris 提供多种数据导入方案,可以针对不同的数据源进行选择不同的数据导入方式。 数据源导入方式对象存储(s3),HDFS使用 Broker 导入数据本地文件Stream Load, MySQL LoadKafka订阅 Kafka 数据Mysql、PostgreSQL&a…...

一. 从Hive开始
1. 怎么理解Hive Hive不能理解成一个传统意义上的数据库,应该理解成一个解决方案。 是Hadoop在hdfs和mapreduce之后才出现的一个结构化数据处理的解决方案。 Hdfs解决了大数据的存储问题,mapreduce解决了数据的计算问题。 一切似乎很美好。 但是使用成本…...
Linux下的PWM驱动
PWM PWM简介⭕ **PWM(Pulse Width Modulation,脉冲宽度调制)**是一种利用微处理器的数字输出对模拟电路进行控制的技术。通过改变脉冲的占空比,可以控制模拟电路的输出电压或电流。PWM技术广泛应用于电机控制、灯光调节、音频信号…...

日语输入法平假名和片假名切换
在学日语输入法的时候,我们在使用罗马音输入的时候,在进行平假名和片假名切换: 1、使用电脑在打字,日语输入法切换的时候使用 Shift Alt 如果日语输入法显示为 A 需要切换为 あ的话可以按Caps Lock键 。(相当于中文…...

Oracle向量搜索及其应用场景
Oracle 向量搜索(AI Vector Search)是一个集成到 Oracle 数据库中的功能,旨在优化人工智能(AI)工作负载。它允许用户存储和查询非结构化数据的语义内容,如文档、图像等,形式为向量。 向量数据类…...

【排序算法】六、快速排序补充:三指针+随机数法
「前言」文章内容是对快速排序算法的补充,之前的算法流程细节多难处理,这里补充三指针随机数法(递归),这个容易理解,在时间复杂度上也更优秀。 快排:三指针随机数法 原理跟之前的一致ÿ…...

PyTorch torch.cdist函数介绍及示例代码
1. torch.cdist 函数介绍 torch.cdist 是 PyTorch 中用于计算两组向量之间成对距离的函数。它可以计算两个张量(矩阵)中的每对向量之间的距离,支持多种距离度量方式,如欧氏距离(默认)或 p 范数距离。 函数原型 torch.cdist(x1, x2, p=2.0, compute_mode=use_mm_for_eu…...

CTK框架(四): 插件编写
目录 1.生成插件 1.1.环境说明 1.2.服务类,纯虚类,提供接口 1.3.实现插件类,实现纯虚函数 1.4.激活插件,加入ctk框架的生命周期中 1.5.添加资源文件 1.6..pro文件 2.使用此插件 3.总结 1.生成插件 1.1.环境说明 编译ct…...

深入理解C代码中的条件编译
引言 条件编译是 C 编程中的一个重要特性,它允许开发人员根据不同的条件选择性地编译源代码的不同部分。这一特性对于编写跨平台的程序、优化代码性能或控制编译时资源消耗等方面非常重要。本文将深入探讨条件编译的工作原理、使用场景、高级应用以及注意事项&…...

Ubuntu16.04操作系统-内核优化
1. 概述 本文所用优化是生产环境中经过长期验证的内核优化策略,针对的服务器与POD主要用于高CPU、高内存、高IO的业务场景。 备注: OS: ubuntu16.04, 内核: 4.15.0-147-generic 主要涵盖以下内容优化: ulimit优化加强tcp参数其他内存参数 …...

Qt/C++编写的Onvif调试助手调试神器工具/支持云台控制/预置位设置等/有手机版本
一、功能特点 广播搜索设备,支持IPC和NVR,依次返回。可选择不同的网卡IP进行对应网段设备的搜索。依次获取Onvif地址、Media地址、Profile文件、Rtsp地址。可对指定的Profile获取视频流Rtsp地址,比如主码流地址、子码流地址。可对每个设备设…...

【原创】java+swing+mysql密码管理器系统设计与实现
个人主页:程序员杨工 个人简介:从事软件开发多年,前后端均有涉猎,具有丰富的开发经验 博客内容:全栈开发,分享Java、Python、Php、小程序、前后端、数据库经验和实战 文末有本人名片,希望和大家…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
