python进阶篇-day09-数据结构与算法(非线性结构与排序算法)
非线性结构(树状结构)
特点: 每个节点都可以有n个子节点(后继节点) 和 n个父节点(前驱节点)
代表: 树, 图......
概述
属于数据结构之 非线性结构的一种, 父节点可以有多个子节点(后续节点)
特点
-
有且只有1个根节点
-
每个节点都可以有1个父节点及任意个子节点, 前提: 根节点除外(没有父节点)
-
没有子节点的节点称之为: 叶子节点
二叉树概念和性质
每个节点最多只能有2个子节点
二叉树分类:
-
完全二叉树: 除了最后1层, 其他层的节点都是满的
-
满二叉树: 包括最后1层, 所有层的节点都是满的
-
不完全二叉树: 某层(不仅仅是最后1层)的节点数量不满
常用二叉树:
-
平衡二叉树: 防止树退化成链表, 指的是: 任意节点的两颗子树的高度差不超过1
-
排序二叉树: 主要是对元素排序的
存储方式
更推荐使用 链表的方式来存储, 每个节点有三部分组成, 分别是: 元素域(数值域), 左子树(地址域), 右子树(地址域)
针对于, 多叉树的情况, 可以将其转成二叉树, 然后再来存储
性质
-
在二叉树的第i层上至多有2i-1 个结点(i>0)eg:第3层最多结点个数2^((3-1))
-
深度为k的二叉树至多有2k - 1个结点(k>0)eg:层次2^((3))-1= 7
-
对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0 = N2+1
-
最多有n个结点的完全二叉树的深度必为log2(n+1)
-
对完全二叉树,若从上至下、从左至右编号,则编号为i的结点,其左孩子编号必为2i,其右孩子编号必为2i+1,其父节点的编号必为i//2(i=1时为根,除外)
二叉树的广度优先
广度优先可以找到最短路径:
相当于层次遍历,先把第层给遍历完,看有没有终点;再把第层遍历完,看有没有重点
插入节点
-
初始操作:
初始化队列、将根节点入队、准备加入到二叉树的新结点
-
重复执行:
获得并弹出队头元素
1、若当前结点的左右子结点不为空,则将其左右子节点入队列
2、若当前结点的左右子节点为空,则将新结点挂到为空的左子结点、或者右子节点
图示

二叉树的深度优先
深度优先往往可以很快找到搜索路径:
比如:先找一个结点看看是不是终点,若不是继续往深层去找,直到找到终点。、中序,先序,后序属于深度优先算法
示例
层次(广度)遍历: 0123456789
先序遍历: 0137849256 根 左 右
中序遍历: 7381940526 左 根 右
后序遍历: 7839415620 左 右 根
图示

二叉树代码演示
# 创建节点类 class Node(object):# 初始化属性def __init__(self, item):self.item = item # 数值域self.lchild = None # 左子树(地址域)self.rchild = None # 左子树(地址域) # 创建二叉树类 class BinaryTree(object):def __init__(self, root: Node = None):self.root = root # 根节点 # 添加元素函数(完全二叉树)def add(self, item):# 判断根节点是否为空if self.root is None:self.root = Node(item)return# 根节点不为空, 找到缺失节点# 创建队列, 用于记录已存在的节点queue = []# 把根节点添加到队列queue.append(self.root)# 循环遍历队列, 直至 把新元素添加到合适的位置while True:# 获取队列中的第一个元素node = queue.pop(0)# 左子树为空if node.lchild is None:node.lchild = Node(item)return # 结束添加动作else:# 左子树存在, 就将其添加到队列中queue.append(node.lchild)# 右子树为空if node.rchild is None:node.rchild = Node(item)return # 结束添加动作else:# 右子树存在, 就将其添加到队列中queue.append(node.rchild) # 广度优先def breadth_travel(self):# 判断根节点是否为空if self.root is None:return # 为空直接结束# 创建队列, 记录所有节点queue = []# 将根节点, 添加到队列中queue.append(self.root)# 只要队列长度大于0, 就说明还有节点, 循环遍历while len(queue) > 0:# 获取队列中的第一元素node = queue.pop(0)# 输出当前节点print(node.item, end='\t')# 判断当前节点的左子树是否为空if node.lchild is not None:# 不为空, 则将左子树入队queue.append(node.lchild)# 判断当前节点的右子树是否为空if node.rchild is not None:# 不为空, 则将左子树入队queue.append(node.rchild) # 深度优先: 先序(根左右)def preorder_travel(self, root):# 判断根节点是否不为空if root is not None:# 中序先输出根节点print(root.item, end='\t')# 递归左子树self.preorder_travel(root.lchild)# 递归右子树self.preorder_travel(root.rchild) # 深度优先: 中序(左根右)def mid_travel(self, root):if root is not None:self.mid_travel(root.lchild)print(root.item, end='\t')self.mid_travel(root.rchild) # 深度优先: 后序(左右根)def poster_travel(self, root):if root is not None:self.poster_travel(root.lchild)self.poster_travel(root.rchild)print(root.item, end='\t')
三. 算法
排序类相关
稳定性: 排序前后的相对位置(相同的元素位置)是否发生变化
稳定排序: 冒泡排序、插入排序、归并排序和基数排序
不稳定排序: 选择排序、快速排序、希尔排序、堆排序
冒泡排序
原理
相邻元素两辆比较, 大的往后走, 这样第一轮比较完毕后, 最大值就在最大索引处
核心
-
比较的总轮数 列表长度 - 1
-
每轮比较的总次数 列表长度 - 1 - 轮数(从0 开始)
-
谁和谁比较(交换) j 和 j + 1 比较
图解

代码
def buble_sort(my_list):# 定义变量n存储列表长度n = len(my_list)# 比较的轮数for i in range(n - 1): # i: 0, 1, 2, 3# 记录交换的次数count = 0# 每轮比较的次数for j in range(n - 1 - i): # j: 4, 3, 2, 1if my_list[j] > my_list[j + 1]:# 交换时计数器加一count += 1my_list[j], my_list[j + 1] = my_list[j + 1], my_list[j]print(f'第 {i} 轮交换了 {count} 次')# 如果当前轮次交换了0次, 则跳出外循环if count == 0:break
if __name__ == '__main__':list1 = [2, 1, 4, 5, 3]buble_sort(list1)print('list1', list1)print('-' * 21)
list2 = [5, 3, 4, 7, 2]buble_sort(list2)print('list2', list2)
冒泡总结
时间复杂度: 最优O(n), 最差O(n²)
遍历一遍发现没有任何元素发生了位置交换,终止排序
算法稳定性:稳定算法
选择排序
原理
第一轮: 假设索引为0的元素时最小值, 依次和后续的元素比较, 只要比该值小, 就纪录住真正最小值的那个索引, 第一轮比较完毕后, 把最小值放到索引为0的位置即可
第二轮: 假设索引为1的元素时最小值, 依次和后续的元素比较, 只要比该值小, 就纪录住真正最小值的那个索引, 第一轮比较完毕后, 把最小值放到索引为1的位置即可
......
解释:
选择排序就是把符合要求的数据选择出来进行排序
核心
-
比较的总轮数 列表长度 - 1
-
每轮比较的总次数 i + 1 ~ 列表的最后1个元素
-
谁和谁比较(交换) j 和 min_index 位置的元素比较
比较过程
具体的比较过程, 假设共 5 个元素 比较的轮数 每轮比较的总次数 谁和谁比较 第0轮 4 0和1, 0和2, 0和3, 0和4 第1轮 3 1和2, 1和3, 1和4 第2轮 2 2和3, 2和4 第3轮 1 3和4
代码
def select_sort(my_list):# 定义变量n存储列表长度n = len(my_list)# 比较的轮数for i in range(n - 1): # i: 0, 1, 2, 3# 记录最小值索引min_idx = i# 每轮比较的次数for j in range(i + 1, n): # j: 4, 3, 2, 1# 判断min_idx后的元素是否比min_idx小if my_list[j] < my_list[min_idx]:# 将最小值索引设为jmin_idx = j# 如果最小值索引等于i说明i的位置是正确的,不交换if min_idx != i:# 交换my_list[i], my_list[min_idx] = my_list[min_idx], my_list[i]
if __name__ == '__main__':list1 = [2, 1, 4, 5, 3]select_sort(list1)print('list1', list1)print('-' * 21)
list2 = [5, 3, 4, 7, 2]select_sort(list2)print('list2', list2)
选择总结
算法稳定性: 不稳定算法
时间复杂度: 最优: O(n²), 最差: O(n²)
插入排序
原理
把要排序的列表分成两部分, 第一部分是有序的(拍好序的), 第二部分是无序的(待排序的), 然后从待排序的列表中, 依次取出每个值, 插入到 排好序的列表的 合适位置 .
核心
-
比较的总轮数 列表长度 - 1 for i in range(1, n)
-
每轮比较的总次数 i ~ 0(逆向遍历) for i in range(i, 0, -1)
-
谁和谁比较(交换) i 和 j 的每个值 比较
比较过程
具体的比较过程, 假设共 5 个元素 比较的轮数 每轮比较的总次数 谁和谁比较 第1轮 4 1和0 第2轮 3 2和1, 2和0 第3轮 2 3和2, 3和1, 3和0 第4轮 1 4和3, 4和2, 4和1, 4和0
代码
def insert_sort(my_list):# 定义变量n存储列表长度n = len(my_list)# 比较的轮数for i in range(1, n): # i: 1, 2, 3, 4# 每轮比较的次数for j in range(i, 0, -1): # j: 1 2,1 3,2,1 4,3,2,1# 判断当前元素(待排序)是否比前面的元素(排好序的)小if my_list[j] < my_list[j - 1]:# 交换当前元素和当前元素的前一个元素my_list[j], my_list[j - 1] = my_list[j - 1], my_list[j]else:break
if __name__ == '__main__':list1 = [2, 1, 4, 5, 3]insert_sort(list1)print('list1', list1)print('-' * 21)
list2 = [5, 3, 4, 7, 2]insert_sort(list2)print('list2', list2)
插入总结
算法稳定性: 稳定算法
时间复杂度: 最优: O(n) 最坏: O(n²)
查找类相关(二分查找)
此处只记录二分查找, 并非查找只有二分查找这一种
介绍
-
概述: 他是一种高效的查找类算法, 也叫: 折半查找
-
细节: 要被查找的列表必须是有序的
-
原理:
-
获取列表的中间位置的元素, 然后和要查找的元素进行比较
-
如果相等, 直接返回结果即可
-
如果比中间值小, 去 中间前 范围查找
-
如果比中间值大, 去 中间后 范围查找
-
递归版
def binary_search(my_list, item):n = len(my_list)if n <= 0:return Falsemid = n // 2if item == my_list[mid]:return Trueelif item < my_list[mid]:return binary_search(my_list[:mid], item)else:return binary_search(my_list[mid + 1:], item)
非递归版
def binary_search(my_list, item):# 计算列表长度n = len(my_list)# 定义初始起始位置为0start = 0# 定义初始终止位置为列表长度减1end = n - 1# 当起始位置大于终止位置时结束循环while start <= end:# 定义中间位置为起始位置加终止位置除2mid = (start + end) // 2# 判断中间索引位置的元素是否为要查找的元素if my_list[mid] == item:return True# 判断中间索引位置的元素比要查找的位置小elif my_list[mid] < item:# 设置起始位置索引为中间位置加1start = mid + 1# 判断中间索引位置的元素比要查找的位置大else:# 设置终止位置索引为中间位置减1end = mid - 1return False if __name__ == '__main__':list1 = [1, 2, 3, 4, 5, 6, 7]print(binary_search(list1, 4))
总结
-
必须采用顺序存储结构
-
必须按关键字大小有序排列
-
时间复杂度: 最优: O(1) 最坏: O(logn)
相关文章:

python进阶篇-day09-数据结构与算法(非线性结构与排序算法)
非线性结构(树状结构) 特点: 每个节点都可以有n个子节点(后继节点) 和 n个父节点(前驱节点) 代表: 树, 图...... 概述 属于数据结构之 非线性结构的一种, 父节点可以有多个子节点(后续节点) 特点 有且只有1个根节点 每个节点都可以有1个父节点及任意个子节点, 前提: 根节点除…...

线性代数基础
Base 对于矩阵 A,对齐做 SVD 分解,即 U Σ V s v d ( A ) U\Sigma V svd(A) UΣVsvd(A). 其中 U 为 A A T AA^T AAT的特征向量,V 为 A T A A^TA ATA的特征向量。 Σ \Sigma Σ 的对角元素为降序排序的特征值。显然,U、V矩阵…...

LCR 021
题目:LCR 021 解法一:计算链表长度 遍历两次,第一次获取链表长度 L(包括虚拟节点),第二次遍历到第 L-n 个节点(从虚拟节点遍历) public ListNode removeNthFromEnd(ListNode head, …...

【阿雄不会写代码】全国职业院校技能大赛GZ036第四套
也不说那么多了,要用到这篇博客,肯定也知道他是干嘛的,给博主点点关注点点赞!!!这样博主才能更新更多免费的教程,不然就直接丢付费专栏里了,需要相关文件请私聊...

Vue组件:使用$emit()方法监听子组件事件
1、监听自定义事件 父组件通过使用 Prop 为子组件传递数据,但如果子组件要把数据传递回去,就需要使用自定义事件来实现。父组件可以通过 v-on 指令(简写形式“”)监听子组件实例的自定义事件,而子组件可以通过调用内建…...

数据分析-埋点
1、数据埋点的定义 针对特定用户行为或事件进行捕获、处理何发送的相关技术及其实施过程。 2、数据埋点的原理 埋点是数据采集的重要方式。通过在页面上植入代码,监控用户行为(例:页面加载、按钮点击等)。用户一旦触发了该事件,就会根据埋点信息将相关数…...

【文心智能体】通过工作流使用知识库来实现信息查询输出,一键查看旅游相关信息,让出行多一份信心
欢迎来到《小5讲堂》 这是《文心智能体平台》系列文章,每篇文章将以博主理解的角度展开讲解。 温馨提示:博主能力有限,理解水平有限,若有不对之处望指正! 目录 创建灵感基本配置头像名称和简介人物设定角色与目标思考路…...

服务器监控工具都是监控服务器的哪些性能和指标
服务器监控工具通常用于确保服务器及其相关服务的正常运行。这些工具可以帮助管理员快速识别并解决问题,从而减少停机时间和性能下降的风险。以下是服务器监控工具通常会监控的一些主要内容: 系统健康状态: CPU使用率 内存(RAM&…...
不小心删除丢失了所有短信?如何在 iPhone 上查找和恢复误删除的短信
不小心删除了一条短信,或者丢失了所有短信?希望还未破灭,下面介绍如何在 iPhone 上查找和恢复已删除的短信。 短信通常都是非正式和无关紧要的,但短信中可能包含非常重要的信息。因此,如果您删除了一些短信以清理 iPh…...

【skyvern 快速上手】一句话让AI帮你实现爬虫+自动化
目录 skyvern介绍主要特点工作流程 部署(重点介绍源码部署)源码部署docker快速部署 运行(基于源码)后端前端 快速使用示例总结 skyvern介绍 Skyvern 是一款利用大语言模型(LLM)和计算机视觉技术来自动化浏…...

【C++ Primer Plus习题】14.1
大家好,这里是国中之林! ❥前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。有兴趣的可以点点进去看看← 问题: 解答: main.cpp #include <iostream> #include "wine.h" …...

在Ubuntu上运行QtCreator相关程序
背景:希望尝试在Linux系统上跑一下使用QtCreator相关的程序,因为有一些工作岗位要求有Linux上使用Qt的经验。 (1)我是把Windows上的程序移过来的,Windows上文件名称是不区分大小写的。 而Ubuntu上是区分的 所以一部分头文件需要进行修改&am…...

MybatisPlus 快速入门
目录 简介 安装 Spring Boot2 Spring Boot3 Spring 配置 Spring Boot 工程 Spring 工程 常见注解 条件构造器 流式查询 使用示例 批量操作 使用示例 自定义SQL Service接口 CRUD 扩展功能 代码生成 安装插件 通用枚举 配置枚举处理器 插件功能 配置示例…...
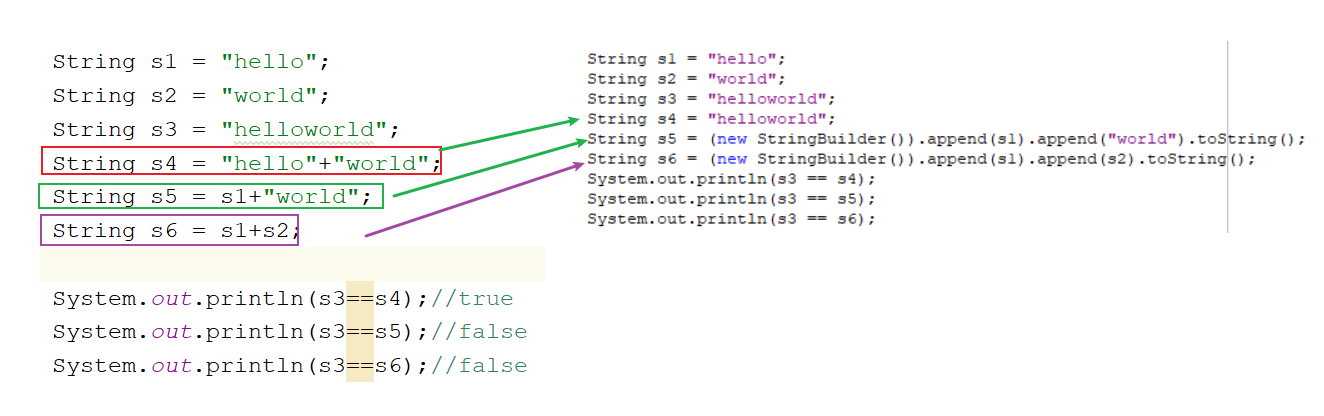
Java.lang中的String类和StringBuilder类介绍和常用方法
目录 Java.lang中的String类和StringBuilder类介绍和常用方法 String类介绍 String类的底层成员介绍 基本介绍 回顾String传址调用问题 String类对象的创建方式 String面试题 创建对象or不创建对象 创建了几个对象and共有几个对象 String常用方法 判断字符串是否相等方法 获取字…...
)
notepad++软件介绍(含安装包)
Notepad 是一款开源的文本编辑器,主要用于编程和代码编辑。它是一个功能强大的替代品,常常被用来替代 Windows 系统自带的记事本。 Notepad win系统免费下载地址 以下是 Notepad 的一些主要特点和功能: 多语言支持:Notepad 支持多…...

chapter13-常用类——(章节小结)——day17
498-常用类阶段梳理...

RTX AI PC 和工作站上部署多样化 AI 应用支持 Multi-LoRA
今天的大型语言模型(LLMs)在许多用例中都取得了前所未有的成果。然而,由于基础模型的通用性,应用程序开发者通常需要定制和调整这些模型,以便专门针对其用例开展工作。 完全微调需要大量数据和计算基础设施࿰…...

C++ STL-deque容器入门详解
1.1 deque容器基本概念 功能: 双端数组,可以对头端进行插入删除操作 deque与vector区别: vector对于头部的插入删除效率低,数据量越大,效率越低deque相对而言,对头部的插入删除速度回比vector快vector访…...

数据结构之折半查找
折半查找(Binary Search),也称为二分查找,是一种在有序数组中查找特定元素的搜索算法。其工作原理是,通过不断将待查找的区间分成两半,并判断待查找的元素可能存在于哪一半,然后继续在存在可能性…...

linux高级学习12
24.9.9学习目录 一.条件变量 一.条件变量 通常条件变量和互斥锁同时使用; 条件变量是用来阻塞线程,其本身并不是锁,直到达到特定的要求; (1)条件变量初始化 #include <pthread.h> int pthread_con…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
