小小GCD、LCM拿下拿下
目录
最大公约数(GCD)
最大公约数(GCD)求解:
一、辗转相除法
二、三目运算符
三、位运算
最大公约数(GCD)模板:
最大公约数(GCD)例题:
最小公倍数(LCM)
最小公倍数(LCM)求解:
最小公倍数(LCM)模板:
最小公倍数(LCM)例题:
GCD、LCM是算法当中的基础之基础,分别对应最大公约数、最小公倍数,在算法竞赛中涉及到的概率也是比较高的,GCD、LCM在小学时就涉及到了求法,本篇将给大家详解GCD、LCM这两个函数,并且提供最简单的模板,在考察时,直接背上即可。

最大公约数(GCD)
也称为最大公因数或最大公因子,是指两个或多个整数共有的约数中最大的一个。在数学中,这是指能够同时被这些整数整除的最大的正整数。例如,8与12的最大公约数为4,4同时能够被8与12整除,找不到x>4同时满足8%x=0且12%x=0这样的数,我们就认为4是8与12的最大公约数(GCD)
最大公约数(GCD)求解:
一、辗转相除法
我们求解最大公约数(GCD)最常用的方法为辗转相除法,就跟小学学的方法一样,具体思路为:设两数为n、m(n>m), 用n除以m,r1为余数:即a÷b=q.....r1。若r1=0,则gcd(a,b)=b;若r1≠0,则再用b除以r1(辗转一下),r2为余数:即b÷r1=q.......r2 。若r2=0,则gcd(a,b)=r1,若r2≠0,则继续用r1除以r2,如此下去,直到能整除为止。其最后一个为被除数的余数的除数即为gcd(a, b)。
例如:a=12,b=8,a%b=4,b%4=0,最后一个为被除数余数的除数就是4,4就是所求最大公约数。

二、三目运算符
实际上,这两种写法在功能上是等价的,都是运用了辗转相除法,都能正确计算出两个整数的最大公约数。它们只是条件判断的表达方式不同,这里的判断条件变为了n>0。不过,第一种写法在n为0时直接返回结果,避免了一次递归调用,可能会有微小的性能优势。但在实际应用中,这种差异通常可以忽略不计,大家觉得哪个好记就记哪个就行。
三、位运算
这种方法使用了位运算和while循环来实现,而不是递归。这种方法通常被称为“二进制GCD算法”或“辗转相除法”的变种。此方法计算gcd的效率非常高效,但是一般人是不知道有这种方法,这里给大家介绍一下,供大家了解,其实真正用起来,基本所有的问题前两种都能够解决,大家根据自己爱好选择学习。
循环的条件是(m%=n)&&(n%=m)。这意味着只要m除以n的余数不为0,并且n除以m的余数也不为0,循环就会继续。在每次循环中,m和n都会更新为它们之间的余数。这个过程会不断重复,直到其中一个变为0,最后返回的是a+b,下面我们模拟一下过程。

最大公约数(GCD)模板:
int gcd(int m,int n){//辗转相除法return n==0?m:gcd(n,m%n);
}
int gcd(int m,int n){//三目运算符实现return n>0?gcd(n,m%n):m;
}
int gcd(int m,int n){//位运算,速度大于前两种while((m%=n)&&(n%=m));return m+n;
}最大公约数(GCD)例题:
AcWing 4199. 公约数
给定两个正整数 a 和 b。
你需要回答 q 个询问。
每个询问给定两个整数 l,r,你需要找到最大的整数 x,满足:
- x 是 a 和 b 的公约数。
- l≤x≤r。
输入格式
第一行包含两个整数 a,b。
第二行包含一个整数 q。
接下来 q 行,每行包含两个整数 l,r。
输出格式
每个询问输出一行答案,即满足条件的最大的 x,如果询问无解,则输出 −1。
数据范围
前六个测试点满足 1≤a,b≤100,1≤q≤20。
所有测试点满足 1≤a,b≤10^9,1≤q≤10^4,1≤l≤r≤10^9。
输入样例:
9 27
3
1 5
10 11
9 11
输出样例:
3
-1
9解题思路:
本题考察为最大公约数+二分查找,首先有了a,b,我们先求出这两个数的最大公约数,即所有的公约数都要小于这个数,那么我们再用试除法求这个最大公约数的因子,最大公约数的因子必然也能被a,b整除,比如12,8,最大公约数为4,4的因子为2,2也能被4整除。这样我们得到一个因子数组,在这个数组里面去查找满足条件的值,既然要二分查找那么就要对此数组进行排序。我们试除法时会产生很多重复的数,排完序这并不影响二分查找,无非是多查找几次,二分的效率是非常高的,无伤大雅。为社么满足nums[mid]<=r的才left=mid;按二分模板来说是l<=nums[mid]<=r,最后为什么还要再判断nums[left]<l||nums[left]>r,这里解释一下:

AC代码:
#include<iostream>
#include<algorithm>
using namespace std;
int a,b,q,l,r;
int nums[10005];
int k;
int gcd(int m,int n){return n>0?gcd(n,m%n):m;
}
void fun(int tmp){//试除法求tmp所有因子nums[k++]=tmp;for(int i=1;i*i<=tmp;i++){//1-sqrt(tmp)范围if(tmp%i==0){//能够整除nums[k++]=i;//自己是因子nums[k++]=tmp/i;//另一个因子的也是}}
}
int main(){cin>>a>>b>>q;int maxgcd=gcd(b,a);//最大公约数fun(maxgcd);sort(nums,nums+k);//排序,有重复的数不用管while(q--){cin>>l>>r;if(l>maxgcd||r<1){//在给定的区间之外cout<<-1<<endl;}else{//二分法求满足条件的最大的公约数int left=0,right=k-1;while(left<right){int mid=left+right+1>>1;if(nums[mid]<=r){left=mid;}else{right=mid-1;}}if(nums[left]<l||nums[left]>r){//若找到的不在区间内cout<<-1<<endl;}else{cout<<nums[left]<<endl;}}}return 0;
}最小公倍数(LCM)
两个或多个整数公有的倍数叫做它们的公倍数,其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。例如:8和12的最小公倍数为24,24%8=0且24%12=0,只要满足8*a=12*b=c,只要我们得到的c是最小的即可。
最小公倍数(LCM)求解:
最小公倍数(LCM)的求解就比较统一化了,没有最大公约数(GCD)的写法这么多了,一般绝大多数人都是使用m*n/gcd(m,n),m*n是必然得到一个公倍数,这个公倍数不确定是不是最小的,我们再去用m与n的最大公约数与得到的公倍数做除法,即:m*n/gcd(m,n),这样便可以得到最小公倍数(LCM),在实现此公式时,为了避免m*n会爆int,我们通常会先让一个数m/gcd(m,n),再去乘n,最终得到m/gcd(m,n)*n。当然你也可以开的大一点long long、int long long。当m/gcd(m,n)时必然得到一个整数,因为gcd(m,n)是n与m的最大公约数(GCD)也是m的约数。
最小公倍数(LCM)模板:
int lcm(int m,int n){return m/gcd(m,n)*n;
}最小公倍数(LCM)例题:
AcWing 3827. 最小正整数
给定两个整数 n 和 k。
请你计算,末尾至少有连续 k 个 0,并且可以被 n 整除的最小正整数。
例如,当 n=375,k=4 时,满足条件的最小正整数为 30000。
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据占一行,包含两个整数 n,k。
输出格式
每组数据输出一行结果,表示满足条件的最小正整数。
数据范围
所有数据满足 1≤T≤10,1≤n≤109,0≤k≤8。
输入样例:
6
375 4
10000 1
38101 0
123456789 8
1 0
2 0
输出样例:
30000
10000
38101
12345678900000000
1
2解题思路:
这道题其实就是求两个数的最小公倍数,一个是n,另一个是1ek。末尾至少有连续 k 个 0,那么最小我们可以取到1ek,并且可以被 n 整除的最小正整数最终答案为lcm(n,1ek),注意此题要开long long。
AC代码:
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;//注意开long long
int T;
ll n,k;
ll gcd(int m,int n){//求gcdreturn n>0?gcd(n,m%n):m;
}
ll lcm(int m,int n){//求lcmreturn m/gcd(m,n)*n;
}
int main(){cin>>T;while(T--){cin>>n>>k;k=pow(10,k);//变为1ekcout<<lcm(n,k)<<endl;//求两个数的最小公倍数即可}return 0;
}最大公约数(GCD)与最小公倍数(LCM)是算法之中最基础的部分,是每一位算法初学者的首选,也是数学之中必学的内容,博主以写此篇总结归纳GCD、LCM供大家参考学习,文章尚有不足,若有错误的地方恳请各位大佬指出。
执笔至此,感触彼多,全文将至,落笔为终,感谢大家的支持。
相关文章:

小小GCD、LCM拿下拿下
目录 最大公约数(GCD) 最大公约数(GCD)求解: 一、辗转相除法 二、三目运算符 三、位运算 最大公约数(GCD)模板: 最大公约数(GCD)例题: 最…...

如何集成Android平台GB28181设备接入模块?
技术优势 大牛直播SDK的Android平台GB28181设备接入模块在适用场景、音视频能力、定位与通信、数据管理、安全性与稳定性、配置与扩展性以及集成与维护等方面均表现出显著的优势。这些优势使得该模块在视频监控、巡检抢修、远程指挥等多个领域具有广泛的应用前景和重要的应用价…...

mysql——关于表的增删改查(CRUD)
目录 比较运算符和逻辑运算符图 一、增加(Create) 1、全列插入 2、指定列插入 二、查询(Retrieve) 1、全列查询 2、指定列查询 3、别名(as) 4、表达式查询 5、去重(distinct) 6、…...

docker 重启容器且修改服务映射端口
要重启 Docker 容器并修改服务的映射端口,可以按照以下步骤进行操作: 1. 停止当前运行的容器 如果你想重新配置端口,通常需要先停止当前运行的容器。你可以使用以下命令停止容器: docker stop <container_name_or_id>2. 删除现有容器 为了修改端口映射,你需要删…...
智能提取:OfficeImagesExtractor让文档图片提取更简单
“科技是国之利器,也是民之福祉。” 在数字化办公日益普及的今天,我们对文档处理的需求也在不断增长。尤其是对于Office文档中的图片、视频和音频等多媒体内容的提取,传统的方法是繁琐且效率低下的。在这样的背景下,一款能够高效、…...
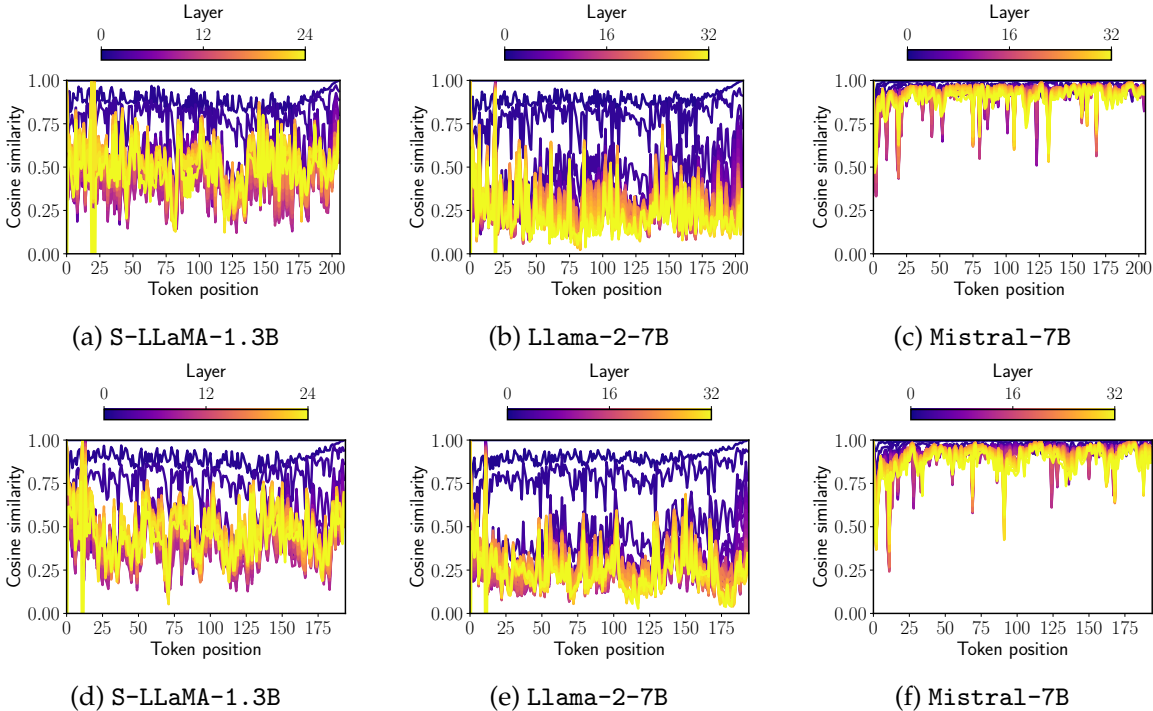
【LLM论文日更】| LLM2Vec揭秘大型语言模型的文本嵌入潜能
论文:https://arxiv.org/pdf/2404.05961代码:https://github.com/McGill-NLP/llm2vec机构:McGill University, Mila ServiceNow Research ,Facebook CIFAR AI Chair领域:embedding model发表:COLM 2024 研…...

大模型微调有必要做吗?LoRa还是RAG?
我需要对大模型做微调吗? 想自定义大模型时,选择:微调还是RAG还是ICL? 需要对大模型做微调? 在人工智能的世界里,大型语言模型(LLM)已经成为了我们探索未知、解决问题的得力助手。…...

机器人外呼系统如何使用呢?
智能电话机器人作为人工智能进入电销行业的一个分类,目前已取得不错的成绩。智能电话机器人针对电销行业的痛点所作出了改善。 作为新兴的一种电销手段,很多企业对其充满好奇又望而却步。那么很多朋友都有想知道为什么现在很多人都用AI机器人拓客&#x…...

python-月份有几天
题目描述 小理现在有一份日历,但是这个日历很奇怪并不能告诉小理日期信息。小理现在有年和月,希望你能帮他计算出来这一年这个月有几天。 输入 输入共一行,两个整数,代表年和月,中间用空格隔开。 输出 一个整数&am…...

1017 Queueing at Bank
链接: 1017 Queueing at Bank - PAT (Advanced Level) Practice (pintia.cn) 题目大意: 有n个客户,k个窗口。已知每个客户的到达时间和需要的时长,如果有窗口就依次过去,如果没有窗口就在黄线外等候(黄线…...
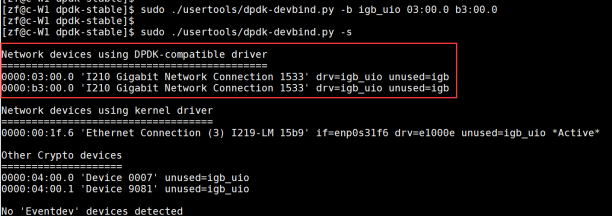
DPDK 测试说明
文章目录 2.DPDK 测试说明2.1硬件pci加密设备绑定到igb_uio驱动IGB_UIO 主要负责什么内容 ? 2.2 test命令使用说明2.3 dpdk-test-crypto-perf命令使用说明2.4 使用testpmd测试网卡性能 2.DPDK 测试说明 2.1硬件pci加密设备绑定到igb_uio驱动 dpdk-stable/usertool…...

上传及接收pdf文件,使用pdfbox读取pdf文件内容
前端上传pdf文件 html <form class"layui-form"><div style"background-color: #ffffff" ><div style"padding: 30px"><div class"layui-form-item"><div class"layui-inline"><label c…...

第一个搭建SpringBoot项目(连接mysql)
首先新建项目找到Spring Initializr 我使用的URL是https://start.spring.io这里最低的JDK版本是17,而且当网速不好的时候可能会显示超时,这里可以选用阿里云的镜像https://start.aliyun.com可以更快一些但是里面还是有一些区别的 我们这里选择Java语言&a…...

docker部署rabbitMQ 单机版
获取rabbit镜像:我们选择带有“mangement”的版本(包含web管理页面); docker pull rabbitmq:management 创建并运行容器: docker run -d --name rabbitmq -p 5677:5672 -p 15677:15672 rabbitmq:management --name:…...

PDF 全文多语言 AI 摘要 API 数据接口
PDF 全文多语言 AI 摘要 API 数据接口 PDF / 文本摘要 AI 生成 PDF 文档摘要 AI 处理 / 智能摘要。 1. 产品功能 支持多语言摘要生成;支持 formdata 格式 PDF 文件流传参;快速处理大文件;基于 AI 模型,持续迭代优化;…...

《信息系统安全》课程实验指导
第1关:实验一:古典密码算法---代换技术 任务描述 本关任务:了解古典密码体制技术中的代换技术,并编程实现代换密码的加解密功能。 注意所有明文字符为26个小写字母,也就是说字母表为26个小写字母。 相关知识 为了完…...

Accelerated Soft Error Testing 介绍
加速软错误测试(Accelerated Soft Error Testing, ASET)是一种评估半导体器件或集成电路(ICs)在高辐射环境中发生软错误率(Soft Error Rate, SER)的方法。这种测试方法通过模拟或加速软错误的发生,以便在较短时间内评估器件的可靠性。软错误指的是那些不会对硬件本身造成…...

Redis缓存常用的读写策略
缓存常用的读写策略 缓存与DB的数据不一致问题,大多数都是指DB的数据已经修改,而缓存中的数据还是旧数据的情况。 旁路缓存模式 对于读操作:基本上所有模式都是先尝试从缓存中读,没有的话再去DB读取,然后写到缓存中…...
9月产品更新 | 超10项功能升级,快来看看你的需求上线了吗?
Smartbi用户可以在官网(PC端下载),更新后便可以使用相关功能,也可以在官网体验中心体验相关功能。 接下来,我们一起来看看都有哪些亮点功能更新吧。 ▎插件商城 Smartbi麦粉社区的应用市场新增了“插件”模块…...

ARP协议工作原理析解 (详细抓包分析过程)
目录 1. ARP 协议 2. 工作原理 3. ARP 协议报文格式 4. ARP 缓存的查看和修改 5. tcpdump 抓包分析 ARP 协议工作原理 5.1 搭建 2 台虚拟机 5.2 在主机 192.168.0.155 打开一个shell命令行开启抓包监听 5.3 在主机 192.168.0.155 打开另一个shell命令行 telnet 192.168.…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
