数学基础 -- 线性代数之LU分解
LU分解
LU分解(LU Decomposition)是线性代数中非常重要的一种矩阵分解方法。它将一个方阵分解为一个下三角矩阵(L矩阵)和一个上三角矩阵(U矩阵)的乘积。在数值线性代数中,LU分解广泛用于求解线性方程组、计算矩阵的行列式以及求逆矩阵等问题。
LU分解的基本概念
给定一个 n × n n \times n n×n 的方阵 A A A,LU分解将其表示为两个矩阵的乘积:
A = L U A = LU A=LU
其中:
- L L L 是一个 n × n n \times n n×n 的下三角矩阵(Lower triangular matrix),即矩阵中的所有元素都位于主对角线及其下方。在标准LU分解中, L L L 的主对角线元素通常为1。
- U U U 是一个 n × n n \times n n×n 的上三角矩阵(Upper triangular matrix),即矩阵中的所有元素都位于主对角线及其上方。
下三角矩阵的行列式
对一个下三角矩阵 L L L,其行列式 det ( L ) \det(L) det(L) 等于主对角线上所有元素的乘积。这是因为在计算行列式时,非对角线上的元素乘积由于是下三角矩阵而为零,最终行列式只取决于主对角线元素的乘积。
假设 L L L 是一个 n × n n \times n n×n 的下三角矩阵,其形式为:
L = ( l 11 0 0 ⋯ 0 l 21 l 22 0 ⋯ 0 l 31 l 32 l 33 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ l n 1 l n 2 l n 3 ⋯ l n n ) L = \begin{pmatrix} l_{11} & 0 & 0 & \cdots & 0 \\ l_{21} & l_{22} & 0 & \cdots & 0 \\ l_{31} & l_{32} & l_{33} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ l_{n1} & l_{n2} & l_{n3} & \cdots & l_{nn} \end{pmatrix} L= l11l21l31⋮ln10l22l32⋮ln200l33⋮ln3⋯⋯⋯⋱⋯000⋮lnn
则 L L L 的行列式为:
det ( L ) = l 11 × l 22 × ⋯ × l n n \det(L) = l_{11} \times l_{22} \times \cdots \times l_{nn} det(L)=l11×l22×⋯×lnn
标准LU分解中的 L L L 的行列式为1
在标准LU分解中,我们要求下三角矩阵 L L L 的主对角线元素全为1,即 l 11 = l 22 = ⋯ = l n n = 1 l_{11} = l_{22} = \dots = l_{nn} = 1 l11=l22=⋯=lnn=1。因此,对于标准LU分解的 L L L 矩阵,其行列式为:
det ( L ) = 1 × 1 × ⋯ × 1 = 1 \det(L) = 1 \times 1 \times \cdots \times 1 = 1 det(L)=1×1×⋯×1=1
举例说明
假设我们有一个3阶矩阵 A A A,经过标准LU分解后得到:
L = ( 1 0 0 l 21 1 0 l 31 l 32 1 ) L = \begin{pmatrix} 1 & 0 & 0 \\ l_{21} & 1 & 0 \\ l_{31} & l_{32} & 1 \end{pmatrix} L= 1l21l3101l32001
则 L L L 的行列式为:
det ( L ) = 1 × 1 × 1 = 1 \det(L) = 1 \times 1 \times 1 = 1 det(L)=1×1×1=1
详细推导示例
为了更清晰地理解,我们可以通过高斯消元的方式来具体推导一个矩阵 A A A 的标准LU分解。
设 A A A 是一个 3 × 3 3 \times 3 3×3 的矩阵:
A = ( 2 − 1 1 4 1 0 − 2 2 5 ) A = \begin{pmatrix} 2 & -1 & 1 \\ 4 & 1 & 0 \\ -2 & 2 & 5 \end{pmatrix} A= 24−2−112105
我们需要通过一系列的初等行变换将 A A A 转化为上三角矩阵 U U U,并记录下消元过程中的乘数构造矩阵 L L L。
步骤1:消去第二行第一个元素
使用第一行的首元2来消去第二行第一个元素4。乘数为:
L 21 = 4 2 = 2 L_{21} = \frac{4}{2} = 2 L21=24=2
然后更新第二行:
第二行 = 第二行 − 2 × 第一行 \text{第二行} = \text{第二行} - 2 \times \text{第一行} 第二行=第二行−2×第一行
得到:
( 2 − 1 1 0 3 − 2 − 2 2 5 ) \begin{pmatrix} 2 & -1 & 1 \\ 0 & 3 & -2 \\ -2 & 2 & 5 \end{pmatrix} 20−2−1321−25
步骤2:消去第三行第一个元素
使用第一行的首元2来消去第三行第一个元素-2。乘数为:
L 31 = − 2 2 = − 1 L_{31} = \frac{-2}{2} = -1 L31=2−2=−1
然后更新第三行:
第三行 = 第三行 + 1 × 第一行 \text{第三行} = \text{第三行} + 1 \times \text{第一行} 第三行=第三行+1×第一行
得到:
( 2 − 1 1 0 3 − 2 0 1 6 ) \begin{pmatrix} 2 & -1 & 1 \\ 0 & 3 & -2 \\ 0 & 1 & 6 \end{pmatrix} 200−1311−26
步骤3:消去第三行第二个元素
使用第二行的次元3来消去第三行第二个元素1。乘数为:
L 32 = 1 3 ≈ 0.333 L_{32} = \frac{1}{3} \approx 0.333 L32=31≈0.333
然后更新第三行:
第三行 = 第三行 − 1 3 × 第二行 \text{第三行} = \text{第三行} - \frac{1}{3} \times \text{第二行} 第三行=第三行−31×第二行
得到:
( 2 − 1 1 0 3 − 2 0 0 5.333 ) \begin{pmatrix} 2 & -1 & 1 \\ 0 & 3 & -2 \\ 0 & 0 & 5.333 \end{pmatrix} 200−1301−25.333
此时,矩阵已经被转换为上三角矩阵 U U U,而消元过程中使用的乘数构成下三角矩阵 L L L:
L = ( 1 0 0 2 1 0 − 1 0.333 1 ) L = \begin{pmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ -1 & 0.333 & 1 \end{pmatrix} L= 12−1010.333001
U = ( 2 − 1 1 0 3 − 2 0 0 5.333 ) U = \begin{pmatrix} 2 & -1 & 1 \\ 0 & 3 & -2 \\ 0 & 0 & 5.333 \end{pmatrix} U= 200−1301−25.333
通过计算,矩阵 L L L 的行列式为:
det ( L ) = 1 × 1 × 1 = 1 \det(L) = 1 \times 1 \times 1 = 1 det(L)=1×1×1=1
总结
在标准LU分解中,要求下三角矩阵 L L L 的主对角线元素为1,因此其行列式为1。这是由行列式的性质和LU分解的定义直接得出的结论。如果我们不要求主对角线元素为1, L L L 的行列式则等于这些主对角线元素的乘积。
相关文章:

数学基础 -- 线性代数之LU分解
LU分解 LU分解(LU Decomposition)是线性代数中非常重要的一种矩阵分解方法。它将一个方阵分解为一个下三角矩阵(L矩阵)和一个上三角矩阵(U矩阵)的乘积。在数值线性代数中,LU分解广泛用于求解线…...

高职人工智能训练师边缘计算实训室解决方案
一、引言 随着物联网(IoT)、大数据、人工智能(AI)等技术的飞速发展,计算需求日益复杂和多样化。传统的云计算模式虽在一定程度上满足了这些需求,但在处理海量数据、保障实时性与安全性、提升计算效率等方面…...

【Java】SpringCloud中使用set方法报错空指针
前言:今天在交流群中看见了一个空指针报错,想着哪里为空点过去看看为什么赋不上值就行,没想到啪啪打脸了,今天总结一下。 以下是他的RedisTempate注入和方法 可以看到,89行报错空指针。先分析一下, ①赋值…...

芯片杂谈 -- 常聊的内核包含哪些模块
目录 1. R52内核速览 2. 处理器模块详解 3.内核的功能安全测什么? 4.小结 最开始接触到汽车MCU大都来自NXP、Infineon、Renesas,例如MPC5748、TC275、RH850 P1X等等; 而各大OEM、供应商等等发布的JD通常都会要求熟悉AURIX、PowerPC、G3K…...

运维问题0002:SAP多模块问题-SAP系统程序在执行时,跳出“加急快件”窗口,提示:快件文档“更新已终止”从作者***收到
1、问题描述 近期收到2起业务报障,均反馈在SAP执行程序时,弹出“加急快件”窗口,导致操作的业务实际没有更新完成。 1)业务场景一:设备管理部门在操作事务代码:AS02进行资产信息变更时,保存正常…...

深度解析RAG:你必须要了解的RAG优化方法
RAG(Retrieval-Augmented Generation)是一种结合检索和生成能力的技术框架,旨在通过从外部知识库中检索相关信息来增强生成模型的输出。其基本思想是利用大型语言模型(LLM)的生成能力,同时通过检索机制获取…...

深度学习驱动下的字符识别:挑战与创新
一、引言 1.1 研究背景 深度学习在字符识别领域具有至关重要的地位。随着信息技术的飞速发展,对字符识别的准确性和效率要求越来越高。字符识别作为计算机视觉领域的一个重要研究方向,其主要目的是将各种形式的字符转换成计算机可识别的文本信息。近年…...

使用 JAXB 将内嵌的JAVA对象转换为 xml文件
使用 JAXB 将内嵌的JAVA对象转换为 xml文件 1. 需求2. 实现(1)FileDesc类(2)MetaFileXml类(3)生成对应的xml文件 1. 需求 获取一个目录下所有文件的元数据信息(文件名、大小、后缀等࿰…...

若依项目后台启动报错: [网关异常处理]、503
拉取代码启动项目,网关控制台报错: 21:31:59.981 [boundedElastic-7] WARN o.s.c.l.c.RoundRobinLoadBalancer - [getInstanceResponse,98] - No servers available for service: ruoyi-system 21:31:59.981 [boundedElastic-7] ERROR c.r.g.h.Gateway…...

【C++ Qt day10】
2、 完善对话框,点击登录对话框,如果账号和密码匹配,则弹出信息对话框,给出提示”登录成功“,提供一个Ok按钮,用户点击Ok后,关闭登录界面,跳转到其他界面 如果账号和密码不匹配&am…...

GO HTTP库使用
Go的 net/http 包是一个强大且易于使用的库,用于构建HTTP服务器和客户端。通过它,你可以轻松实现HTTP请求的处理、路由、静态文件服务等功能。下面重点以及一个简单的Demo示例。 文章目录 1. **基础HTTP服务器**2. **处理请求与响应**3. **路由与处理器*…...

数据结构 - 顺序表
0.线性表 1.定义 线性表就是零个或多个相同数据元素的有限序列。 2.线性表的存储结构 ①.顺序结构 ②.链式结构 3.线性表的表示方法 例如: 一.线性表的基本运算 二.线性表的复杂运算 1.线性表的合并运算 2.线性表的去重运算 三.顺序表 1.定义 顺序表,就…...

企业如何组建安全稳定的跨国通信网络?
组建一个安全稳定的跨国通信网络对于现代企业来说至关重要,尤其是当企业在全球范围内运营时。以下是一些关键步骤和考虑因素: 需求分析: 确定企业的具体通信需求,包括带宽要求、延迟敏感度、数据类型(如语音、视频、文…...

OCR在线识别网站现已上线!
注意,本文只提供学习的思路,严禁违反法律以及破坏信息系统等行为,本文只提供思路 如有侵犯,请联系作者下架 由作者亲自开发的ocr识别网站哈哈,暂时汇聚了三十多种验证码模型以及算法,欢迎各路朋友去尝试,网站地址如下 http://gbj5w3.natappfree.cc/ocr 验证码类型包括但…...

排名再升2位 中国平安位列BrandZ最具价值中国品牌第9位
9月10日,凯度华通明略发布“2024年BrandZ最具价值中国品牌”榜单,中国平安位列榜单第9位,较2023年榜单排名上升2位,品牌价值韧性增长至205.14亿美元,十度蝉联中国保险行业品牌价值第一位。榜单特别提到,中国…...

k8s集群部署:环境准备
本教程基于centos9 arm架构展开。 1. 设置主机名 为每个节点设置主机别名,以便于集群中的角色识别: # 设置主节点的主机名为 kmaster sudo hostnamectl set-hostname kmaster --static# 设置工作节点1的主机名为 kworker1 sudo hostnamectl set-hostn…...

<C++> set、map模拟实现
目录 一、适配器红黑树 二、红黑树再设计 1. 重新设计 RBTree 的模板参数 2. 仿函数模板参数 3. 正向迭代器 构造 operator*() operator->() operator!() operator() operator--() 正向迭代器代码 4. 反向迭代器 构造 operator* operator-> operator operator-- operat…...

软考学习 数据结构 查找
1. 顺序查找(Sequential Search) 基本原理: 顺序查找是一种最简单、最直观的查找算法。它从数据集合的第一个元素开始,依次与目标元素进行比较,直到找到目标元素或遍历完所有元素为止。 适用条件: 适用…...

h264 视频流中添加目标检测的位置、类型信息到SEI帧
在 H.264 视频编码中,SEI(Supplemental Enhancement Information)消息用于传输额外的、非编码的数据,例如目标检测的信息。SEI 数据可以嵌入到 H.264 流中,以在解码过程中传递这些附加信息。 一、步骤 确定 SEI 类型&…...
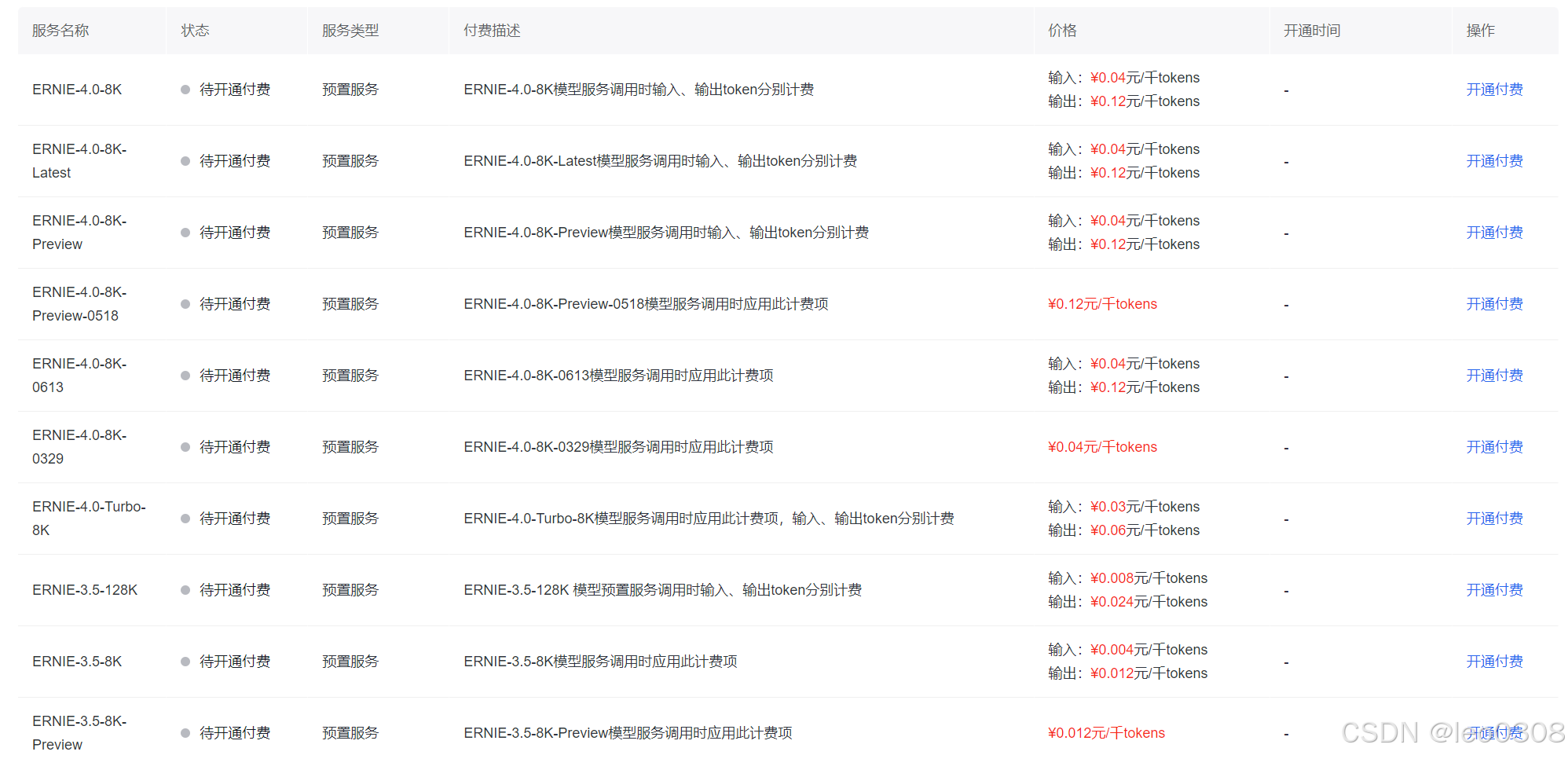
大模型api谁家更便宜
1 openai 可点此链接查询价格:https://openai.com/api/pricing/ 2 百度 可点此链接查询价格:https://console.bce.baidu.com/qianfan/chargemanage/list 需要注意,百度千帆平台上还提供其他家的模型调用服务, 如llama, yi-34b等…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
