代码随想录算法训练营第二十三天| 455. 分发饼干、376. 摆动序列、53. 最大子序和
今日内容
- 贪心理论基础
- Leetcode. 455 分发饼干
- Leetcode. 376 摆动序列
- Leetcode. 53 最大子序和
贪心理论基础
贪心算法的本质就是选择每一阶段的最优,达到全局上的最优。
贪心算法和之前学到的所有方法相比,它没有固定的使用套路,也没有固定的验证法来确认本题是否适用贪心算法。
对于何时应该使用贪心,那就只能手动模拟推导一下。如果模拟推导感觉可以根据局部最优推出全局最优,并且也找不出反例的话,就用贪心吧。
Leetcode. 455 分发饼干
文章链接:代码随想录 (programmercarl.com)
题目链接:455. 分发饼干 - 力扣(LeetCode)
本题的局部最优就是拿目前最大的饼干来满足胃口最大的孩子,从而达到全局最优:尽可能多的孩子被喂饱。而且似乎也找不出反例,那么就可以使用贪心算法解决。

因此,可以写出如下代码:
class Solution {// 从大到小进行贪心public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int index = s.length - 1;int result = 0;for (int i = g.length - 1; i >= 0; i--){ // 注意这里遍历的是 胃口if (index >= 0 && s[index] >= g[i]){index--;result++;}}return result;}
}- 时间复杂度:O(nlogn)
- 空间复杂度:O(1)
注意代码中,for 循环是在表示小孩胃口的数组中进行遍历的,这样是必须的。因为假如对饼干尺寸数组进行遍历,则可能遇到如下图所示情况:

即 饼干尺寸数组遍历完也找不到一个匹配当前孩子胃口的结果,进而影响结果。如果我们的贪心思想是先用尺寸小的饼干满足小胃口的孩子优先的话,此时遍历饼干尺寸数组是正确的。
Leetcode. 376 摆动序列
文章链接:代码随想录 (programmercarl.com)
题目链接:376. 摆动序列 - 力扣(LeetCode)
本题的局部思想就是获取单调坡上的两端节点,不理会单调坡中间的节点,获取两个局部峰值。使整个序列的局部峰值最多,就可以获得全局最优:得到最长摆动序列。

要想知道当前节点是否为单调坡的两端,就需要知晓该节点的前坡值 pre 和 后坡值 next。其中 pre = nums[i] - nums[i - 1],next = nums[i + 1] - nums[i]。当 pre > 0, next < 0 或 pre < 0, next > 0时就说明当前节点是坡的两端。
知晓了两端的判断方式,就需要列出单调坡中可能出现的情况:
- 上下坡中有平坡。
 如图所示,此时要么去除前三个重复元素,要么去除后三个重复元素。
如图所示,此时要么去除前三个重复元素,要么去除后三个重复元素。 所以考虑这种情况后,上面的条件就变为了 当 pre >= 0, next < 0 或 pre <= 0, next > 0 时就说明当前节点是坡的两端。
所以考虑这种情况后,上面的条件就变为了 当 pre >= 0, next < 0 或 pre <= 0, next > 0 时就说明当前节点是坡的两端。 - 数组首位两端。假如整个数组只有两个元素,根据上述的前后坡值是无法计算出来的,因为这样需要三个元素得出。因此可以假设最左边的元素前有个平坡,然后最右边的元素自动视作是一个峰值。

根据上述两种情况可以写出如下代码:
// 版本一
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if (nums.size() <= 1) return nums.size();int curDiff = 0; // 当前一对差值int preDiff = 0; // 前一对差值int result = 1; // 记录峰值个数,序列默认序列最右边有一个峰值for (int i = 0; i < nums.size() - 1; i++) {curDiff = nums[i + 1] - nums[i];// 出现峰值if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {result++;}preDiff = curDiff;}return result;}
};但这个代码依然完成不了,原因就在于 preDiff = curDiff 这一行。
实际上,除了上述两个情况以外还有一个情况:单调坡上有个平坡。
面对这种情况,如果根据 版本一 的代码所示,遍历每个元素时都更新一次前坡值,那么它会把第三个 2 认为是一次摆动,但实际上这只是单调坡上的平坡的一个转折点,并没有摆动。
要想解决该情况,则需要在摆动真正发生时更新前坡值。因此,改良后的代码如下:
class Solution {public int wiggleMaxLength(int[] nums) {int pre = 0;int cur = 0;int result = 1; // 默认最右边的元素算一个摆动序列for (int i = 0; i < nums.length - 1; i++){ // 注意条件表达式已经将最后一个元素排除cur = nums[i + 1] - nums[i];if (pre >= 0 && cur < 0 || pre <= 0 && cur > 0){result++;pre = cur; // 摆动发生时才更新前坡值}}return result;}
}- 时间复杂度:O(n)
- 空间复杂度:O(1)
Leetcode. 53 最大子序和
文章链接:代码随想录 (programmercarl.com)
题目链接:53. 最大子数组和 - 力扣(LeetCode)
本题的局部最优就是当前元素若加入进来后导致总和为负数后,则重新求和。因为本题要求最大的连续子序,所以当总和为负数后,总是会拉低得到的结果,因此碰到使总和为负数的元素时就重置总和。
本题思路如下图所示:
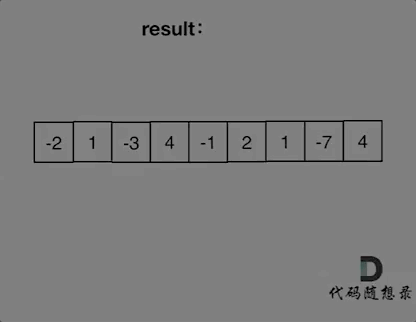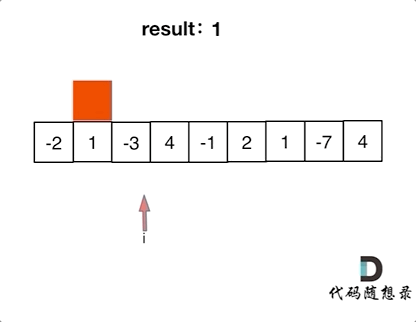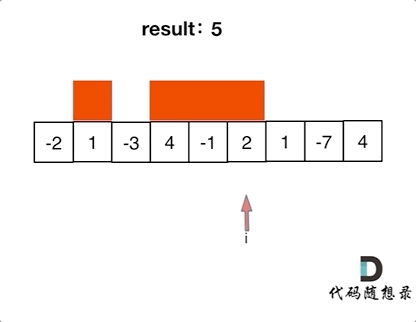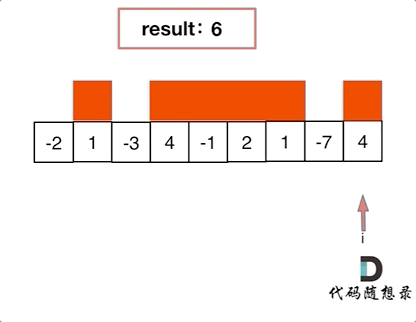
写出如下代码:
class Solution {public int maxSubArray(int[] nums) {int result = Integer.MIN_VALUE;int count = 0;for (int i = 0; i < nums.length; i++){count += nums[i];if (count > result){ // 记录当前最大总和result = count;}if (count < 0){count = 0;} // 当总和为负数时,重置}return result;}
}- 时间复杂度:O(n)
- 空间复杂度:O(1)
总结
贪心算法真是给了个下马威,一下子难以彻底消化贪心算法的使用。
目前看来,贪心算法最重要的还是找到题目中什么是局部最优,这样才好进行下一步。
相关文章:

代码随想录算法训练营第二十三天| 455. 分发饼干、376. 摆动序列、53. 最大子序和
今日内容 贪心理论基础Leetcode. 455 分发饼干Leetcode. 376 摆动序列Leetcode. 53 最大子序和 贪心理论基础 贪心算法的本质就是选择每一阶段的最优,达到全局上的最优。 贪心算法和之前学到的所有方法相比,它没有固定的使用套路,也没有固…...
react js 路由 Router
完整的项目,我已经上传了 资料链接 起因, 目的: 路由, 这部分很难。 原因是, 多个组件,进行交互,复杂度比较高。 我看的视频教程 1. 初步使用 安装: npm install react-router-dom 修改 index.js/ 或是 main.js 把 App, 用 BrowserRouter 包裹起来 2. Navigate 点击…...
AplPost使用
请求get 方法 1,添加token 2,填写get 的参数 2,post方法 把对象的形式直接复制到row里面 3,delete方法 可以直接后面拼接参数...
【Qt】Qt与Html网页进行数据交互
前言:此项目使用达梦数据库,以Qt制作服务器,Html制作网页客户端界面,可以通过任意浏览器访问。 1、Qt与网页进行数据交互 1.1、第一步:准备qwebchannel.js文件 直接在qt的安装路径里复制即可 1.2、第二步…...

教师节特辑:AI绘制的卡通人物,致敬最可爱的人
【编号:9】教师节到了,今天我要分享一组由AI绘制的教师节主题卡通人物插画,每一幅都充满了对老师的敬意和爱戴。让我们一起用这些可爱的卡通形象,向辛勤的园丁们致敬! 🎓【教师形象】 这…...

SprinBoot+Vue智慧农业专家远程指导系统的设计与实现
目录 1 项目介绍2 项目截图3 核心代码3.1 Controller3.2 Service3.3 Dao3.4 application.yml3.5 SpringbootApplication3.5 Vue 4 数据库表设计5 文档参考6 计算机毕设选题推荐7 源码获取 1 项目介绍 博主个人介绍:CSDN认证博客专家,CSDN平台Java领域优质…...

AI大模型行业专题报告:大模型发展迈入爆发期,开启AI新纪元
大规模语言模型(Large Language Models,LLM)泛指具有超大规模参数或者经过超大规模数据训练所得到的语言模型。与传统语言模型相比,大语言模型的构建过程涉及到更为复杂的训练方法,进而展现出了强大的自然语言理解能力…...
FLV 格式详解资料整理,关键帧格式解析写入库等等
FLV 是一种比较简单的视频封装格式。大致可以分为 FLV 文件头,Metadata元数据,然后一系列的音视频数据。 资料够多: FLV格式解析图 知乎用户 Linux服务器研究 画了一张格式解析图,比较全,但默认背景是白色ÿ…...

《深度学习》OpenCV 高阶 图像直方图、掩码图像 参数解析及案例实现
目录 一、图像直方图 1、什么是图像直方图 2、作用 1)分析图像的亮度分布 2)判断图像的对比度 3)检测图像的亮度和色彩偏移 4)图像增强和调整 5)阈值分割 3、举例 二、直方图用法 1、函数用法 2、参数解析…...

coredump-N: stack 消耗完之后,用户自定义信号处理有些问题 sigaltstack
https://mzhan017.blog.csdn.net/article/details/129401531 在上面一篇是关于stack耗尽的一个小程序例子。 https://www.man7.org/linux/man-pages/man2/sigaltstack.2.html 这里提到一个问题,就是如果栈被用光了,这个时候SIGSEGV的用户自定义的handler处理可能就没有空间进…...

数据库有关c语言
数据库的概念 SQL(Structured Query Language)是一种专门用来与数据库进行交互的编程语言,它允许用户查询、更新和管理关系型数据库中的数据。关系型数据库是基于表(Table)的数据库,其中表由行(…...
【网页播放器】播放自己喜欢的音乐
// 错误处理 window.onerror function(message, source, lineno, colno, error) {console.error("An error occurred:", message, "at", source, ":", lineno);return true; };// 检查 particlesJS 是否已定义 if (typeof particlesJS ! undefi…...
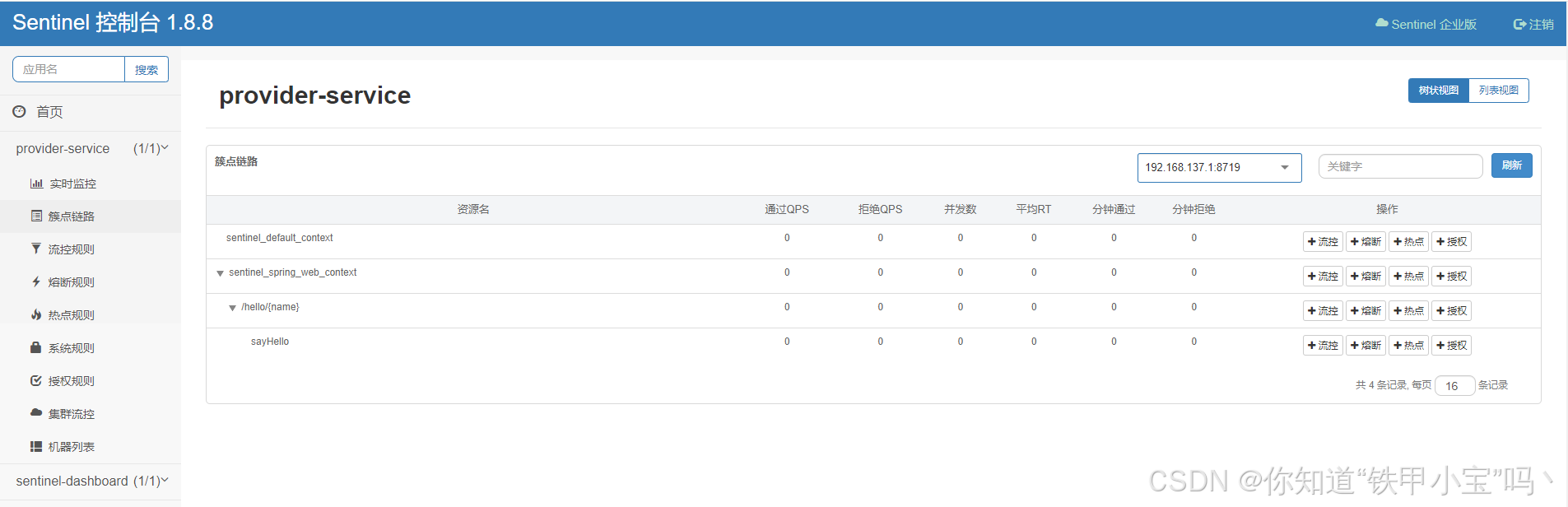
【第27章】Spring Cloud之适配Sentinel
文章目录 前言一、准备1. 引入依赖2. 配置控制台信息 二、定义资源1. Controller2. Service3. ServiceImpl 三、访问控制台1. 发起请求2. 访问控制台 总结 前言 Spring Cloud Alibaba 默认为 Sentinel 整合了 Servlet、RestTemplate、FeignClient 和 Spring WebFlux。Sentinel…...
怎么debug python
1、打开pycharm,新建一个python程序,命名为excel.py。 2、编写代码。 3、点击菜单栏中的“Run”,在下拉菜单中选择“debug excel.py”或者“Debug...”,这两个功能是一样的,都是调试功能。 4、调试快捷键:C…...
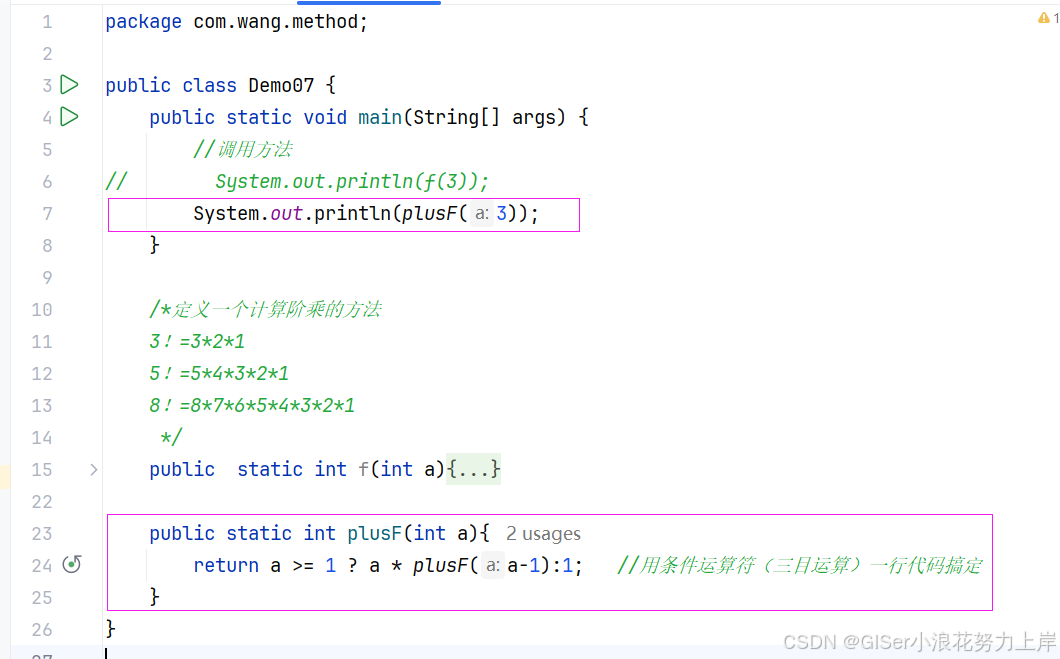
Java 递归
目录 1.A方法调用B方法,很容易理解! 2.递归:A方法调用A方法,就是自己调用自己! 3. 递归的优点: 4. 递归结构包括两个部分: 5. 递归的三个阶段 6. 递归的缺点&#…...

获取业务库的schema信息导出成数据字典
获取业务库的schema信息导出成数据字典 场景:需要获取业务库的schema信息导出成数据字典,以下为获取oracle与mysql数据库的schema信息语句 --获取oracle库schema信息 selecttt1.owner as t_owner,tt1.table_name,tt1.column_name,tt1.data_type,tt1.dat…...

力扣: 快乐数
文章目录 需求分析代码结尾 需求 编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。 …...

一般位置下的3D齐次旋转矩阵
下面的矩阵虽然复杂,但它的逆矩阵求起来非常简单,只需要在 sin θ \sin\theta sinθ 前面加个负号就是原来矩阵的逆矩阵。 如果编程序是可以直接拿来用的,相比其它获取一般旋转轴不经过原点的三维旋转矩阵的途径或算法,应该能…...

每日一题——第八十六题
题目:写一个函数,输入一个十进制的数,将其转换为任意的r进制数 #include<stdio.h> void convertToBaseR(int num, int r); int main() {int num, r;printf("请输入十进制的整数:");scanf_s("%d", &…...

十、组合模式
组合模式(Composite Pattern)是一种结构型设计模式,它允许将对象组合成树形结构来表示“部分-整体”的层次关系。组合模式能够让客户端以统一的方式对待单个对象和对象集合,使得客户端在处理复杂树形结构的时候,可以以…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...
