AI基础 L19 Quantifying Uncertainty and Reasoning with Probabilities I 量化不确定性和概率推理
Acting Under Uncertainty
1 Reasoning Under Uncertainty
• Real world problems contain uncertainties due to:
— partial observability,
— nondeterminism, or
— adversaries.
• Example of dental diagnosis using propositional logic
T oothache ⇒ C av ity
• However inaccurate, not all patients with toothaches have cavities
T oothache ⇒ C av ity ∨ GumP roblem ∨ Abscess . . .
• In order to make the rule true, we have to add an almost unlimited list of possible problems.
• The only way to fix the rule is to make it logically exhaustive
在现实世界中,由于部分可观察性、非确定性或对抗性,问题往往包含不确定性。例如,在牙科诊断中,我们可以使用命题逻辑来表达规则,如“牙痛 ⇒ 蛀牙”。然而,这个规则并不准确,因为并非所有有牙痛的患者都有蛀牙。
为了使这个规则在逻辑上正确,我们需要添加一个几乎无限的可能的疾病列表。例如,我们可以修改规则为“牙痛 ⇒ 蛀牙 ∨ 牙龈问题 ∨ 脓肿…”。这样,我们试图通过逻辑上详尽的方式来修复规则,使其更加准确。
在处理不确定性时,我们通常需要使用概率逻辑或模糊逻辑等技术,这些技术可以更好地处理真实世界中的不确定性和模糊性。例如,模糊逻辑允许我们表达和处理模糊的概念,如“有些”或“大多数”,而不是简单的“是”或“否”。
• Rational agents much choose the right thing, which depends on:
— relative importance of the various goals
— the likelihood that, and degree to which, goals will be achieved.
• Large domains such as medical diagnosis fail for three main reasons:
— Laziness: it is too much work to list complete set of logic rules 工作量大
— Theoretical ignorance: medical science has no complete theory for the domain 理论不完整
— Practical ignorance: even if we know all rules, uncertainty from partial observability
• An agent only has a degree of belief in the relevant sentences. 不确定性
• Probability Theory
— tool to deal with degrees of belief of relevant sentences.
— summarises the uncertainty that comes from our laziness and ignorance.
• Uncertainty and rational decisions
— An agent requires preference among different possible outcomes of various plans
— Utility Theory: defines the quality of the outcome being useful
◦ Every state has a degree of usefulness/utility
◦ Agent prefers higher utility
— Decision Theory: Preferences (Utility Theory) combined with probabilities
◦ Decision theory = probability theory + utility theory
◦ agent is rational if and only if it chooses the action that yields the highest expected utility,
averaged over all the possible outcomes of the action.
◦ principle of maximum expected utility (MEU).
理性代理需要在其不同的计划的各种可能结果之间进行偏好排序。效用理论(Utility Theory)定义了结果的质量,即结果的效用。
- 效用 utility:每个状态都有一个效用度,它表示该状态对代理的有用程度。
- 偏好 preference:代理更倾向于具有更高效用的状态。


Probability Theory
• How can we deal with complex rules which are not always true?
• We extend propositional logic to deal with probabilities.
• We associate a degree of belief with each proposition.
— P (h) = 0.5
• Here, h is a random variable.
• It has a domain of values it can take on (e.g., {true, false})
• Random variables can be
— Boolean: as above, with domain {true, false}
— Discrete: taking on values from some countable domain. E.g. Weather can be sunny,
rainy, windy, or cloudy.
— Continuous: taking on values from the set of real numbers.
我们可以为命题“h”分配一个概率值 P(h) = 0.5。在这里,h 是一个随机变量,它有一个可以取值的域(例如,{true, false})。随机变量可以是布尔型、离散型或连续型。
- 布尔型随机变量:如上所述,其域为 {true, false}。
- 离散型随机变量:取值来自某个可数域。例如,天气可以是晴天、雨天、风天或多云。
- 连续型随机变量:取值来自实数集。
通过这种方式,我们可以表达命题的不确定性。例如,如果一个命题“h”的真实性是不确定的,我们可以将其概率设置为 0.5,表示我们对这个命题的信念程度是中等的。
• In logic, we had a number of possible worlds
— one had to be true;
— all others had to be false
• Probability theory talks about how probable each possible world is:
— Ω (uppercase omega) refers to the sample space
(the set of all possible worlds)
— ω (lowercase omega) refers to one such world
• A fully specified probability model
associates a probability P (ω) ∈ [0, 1] to each possible world
—![]()
— We can use logical formula to specify possible worlds and obtain the probability of all
the worlds in which the formula holds, so for any proposition φ, ![]()
我们可以使用逻辑公式来指定可能的世界,并计算公式成立的世界的概率。对于任何命题 φ,命题 φ 成立的世界的概率 P(φ) 等于所有满足 φ 的世界 ω 的概率之和
Basic Notation
• Prior, or unconditional probabilities measure the degree of belief associated with
some proposition in the absence of any other information.
• For example: P (coin = heads) = 0.5 (abbreviated P (heads) = 0.5)
• A probability distribution captures the probability of each possible value of the
proposition
E.g. Fair Coin P (coin)
— P (heads) = 0.5
— P (tails) = 0.5
— We write this P (coin) : P (coin = h) = 0.5, P (coin = t) = 0.5
- 先验概率或无条件概率:这些概率衡量了在没有其他信息的情况下,某个命题的信念程度。
- 示例:P(coin = heads) = 0.5(简写为 P(heads) = 0.5),这表示公平硬币出现正面的概率是 0.5。
- 概率分布:概率分布捕捉了命题每个可能值的概率。
- 公平硬币的例子:P(heads) = 0.5,P(tails) = 0.5。
Conditional or posterior probability: given evidence that has happened, degree of
belief of new event

条件概率或后验概率是指在已经发生某些证据的情况下,对某个新事件的信念程度。
条件概率的表示方法:
- 给定 b 的事件 a 的概率:P(a | b) = P(a ∧ b) / P(b)
- 也可以写作乘积规则:P(a ∧ b) = P(a | b)P(b)
例如,掷一个公平骰子时,如果第一次骰子掷出 5,那么掷出双倍(两个骰子都是 5)的概率是 P(doubles | Die1 = 5) = P(doubles ∧ Die1 = 5) / P(Die1 = 5)。
条件概率是处理实际问题时非常重要的概念,因为它允许我们在已知某些信息的情况下,对其他事件进行概率推理。在决策制定和数据分析中,条件概率经常被用来估计未来事件的可能性。
Joint Probability Distribution
• A joint probability distribution captures the probability distribution of a set of
variables. E.g. P (coin, die)
• In the above examples, we have seen that P (a ∧ b) = P (a) ∗ P (b)
Warning: not always true!
• This only works when a and b are independent, formally, when
P (b | a) = P (b)
• E.g. a ≡ it rains today, b ≡ it rains tomorrow:
P (b | a) > P (b)
• Thus, in general: P (a ∧ b) = P (b | a)P (a) (conditional probability)
Notice this also means that P (a ∧ b) = P (a | b)P (b)
联合概率分布(Joint Probability Distribution)捕捉了一组变量的概率分布。例如,P(coin, die) 表示同时掷一个硬币和一个骰子的概率分布。
在之前的例子中,我们看到了 P(a ∧ b) = P(a) * P(b) 的规则,这通常适用于独立事件。然而,这并不总是正确的!这个规则只有在 a 和 b 是独立事件时才成立,在数学上,这表示 P(b | a) = P(b)。
例如,考虑两个事件:a ≡ 今天下雨,b ≡ 明天下雨。在这种情况下,P(b | a)(在已知今天下雨的情况下明天也下雨的概率)通常大于 P(b)(明天下雨的概率),因为今天下雨可能增加明天也下雨的可能性。
因此,在一般情况下,P(a ∧ b) = P(b | a)P(a)(条件概率)。这也意味着 P(a ∧ b) = P(a | b)P(b),这实际上是条件概率的另一种表示形式。
相关文章:

AI基础 L19 Quantifying Uncertainty and Reasoning with Probabilities I 量化不确定性和概率推理
Acting Under Uncertainty 1 Reasoning Under Uncertainty • Real world problems contain uncertainties due to: — partial observability, — nondeterminism, or — adversaries. • Example of dental diagnosis using propositional logic T oothache ⇒ C av ity • H…...

C++ 关于时间的轮子
时间字符串转chrono::system_clock std::chrono::system_clock::time_point parse_date(const std::string& date_str) {std::tm tm {};std::istringstream ss(date_str);ss >> std::get_time(&tm, "%Y-%m-%d"); // 假设日期字符串格式为YYYY-MM-DDr…...

阿里达摩院:FunASR - onnxruntime 部署
阿里达摩院:FunASR - onnxruntime 部署 git clone https://github.com/alibaba/FunASR.git 切换到 onnxruntime cd FunASR/runtime/onnxruntime1下载 onnxruntime wget https://isv-data.oss-cn-hangzhou.aliyuncs.com/ics/MaaS/ASR/dep_libs/onnxruntime-linux-x64-1.14.0.t…...
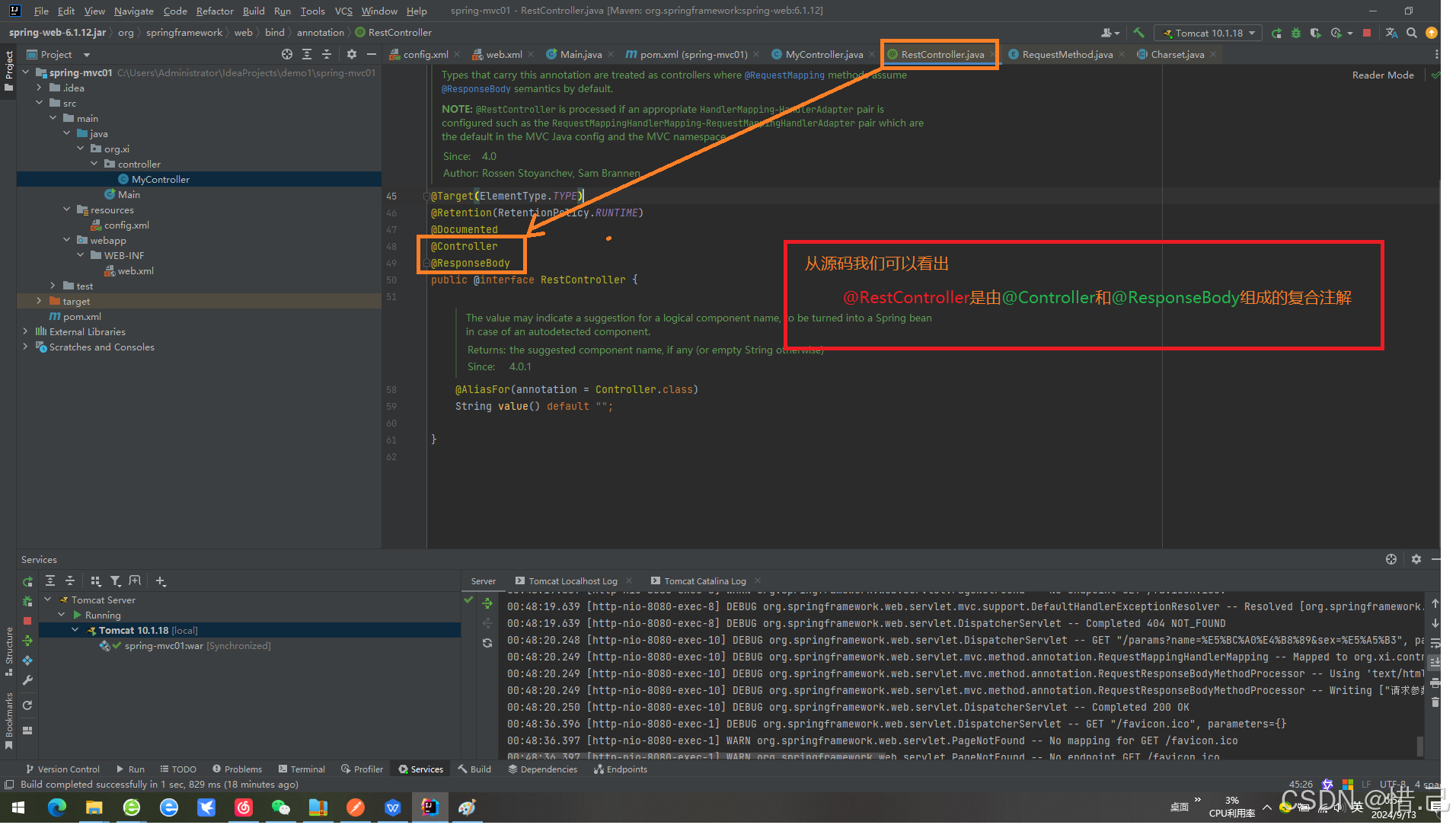
SpringMvc注解
SpringMvc注解 1 SpringMcv基础环境搭建 注:如果已经有SpringMvc项目直接跳过这个就可以了 1 新建项目 2.修改文件为packaging 为war包 <packaging>war</packaging> <?xml version"1.0" encoding"UTF-8"?> <pr…...

队列的基本概念及顺序实现
队列的基本概念 队列的定义 队列(Queue)简称队,也是一宗操作受限的线性表,只允许在表的一段进行插入,而在表的另一端进行删除。向队列中插入元素成为入队或进队;删除元素成为出队或离队。 特性:先进先出 (Fir…...

Leetcode 最长连续序列
算法流程: 哈希集合去重: 通过将数组中的所有元素放入 unordered_set,自动去除重复元素。集合的查找操作是 O(1),这为后续的快速查找提供了保证。 遍历数组: 遍历数组中的每一个元素。对于每个元素,首先检…...

linux网络编程——UDP编程
写在前边 本文是B站up主韦东山的4_8-3.UDP编程示例_哔哩哔哩_bilibili视频的笔记,其中有些部分博主也没有理解,希望各位辩证的看。 UDP协议简介 UDP 是一个简单的面向数据报的运输层协议,在网络中用于处理数据包,是一种无连接的…...

第四部分:1---文件内核对象,文件描述符,输出重定向
目录 struct file内核对象: 如何读写文件? 文件描述符在文件描述符表中的分配规则: 输出重定向初步解析: dup2实现复制文件描述符: struct file内核对象: struct file 是在内核空间中创建的用于描述文…...

如何在开发与生产环境中应用 Flask 进行数据库管理:以 SQLAlchemy 和 Flask-Migrate 为例
在使用 Flask 进行开发时,数据库管理是一个至关重要的环节。借助 SQLAlchemy 作为 ORM(对象关系映射)工具和 Flask-Migrate 进行数据库迁移,开发者可以高效地进行数据库管理,并在不同的环境(如开发环境和生…...
【Java零基础】Java核心知识点之:Map
HashMap(数组链表红黑树) HashMap 根据键的 hashCode 值存储数据,大多数情况下可以直接定位到它的值,因而具有很快的访问速度,但遍历顺序却是不确定的。 HashMap 最多只允许一条记录的键为 null,允许多条记录的值为 null。HashMa…...

9.12日常记录
1.extern关键字 1)诞生动机:在一个C语言项目中,需要再多个文件中使用同一全局变量或是函数,那么就需要在这些文件中再声明一遍 2)用于声明在其他地方定义的一个变量或是函数,在当前位置只是声明,告诉编译器…...

光纤的两种模式
光纤主要分为两种模式:单模光纤(Single-Mode Fiber, SMF)和多模光纤(Multi-Mode Fiber, MMF)。这两种光纤在传输特性、应用场景以及传输距离上存在显著差异。12 单模光纤 定义:单模光纤…...
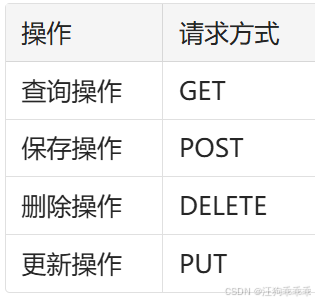
SpringMVC的初理解
1. SpringMVC是对表述层(Controller)解决方案 主要是 1.简化前端参数接收( 形参列表 ) 2.简化后端数据响应(返回值) 1.数据的接受 1.路径的匹配 使用RequestMapping(可以在类上或在方法上),支持模糊查询,在内部有method附带…...
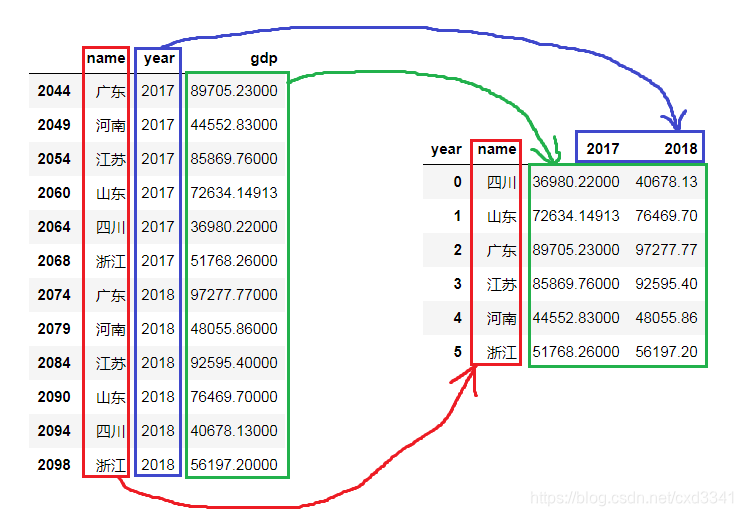
Python 基本库用法:数学建模
文章目录 前言数据预处理——sklearn.preprocessing数据标准化数据归一化另一种数据预处理数据二值化异常值处理 numpy 相关用法跳过 nan 值的方法——nansum和nanmean展开多维数组(变成类似list列表的形状)重复一个数组——np.tile 分组聚集——pandas.…...

Android Greendao的数据库复制到设备指定位置
方法如下: private void export() {// 确保您已经请求并获得了WRITE_EXTERNAL_STORAGE权限// 获取要储存的设备路径String picturesDirPath Environment.getExternalStoragePublicDirectory(Environment.DIRECTORY_PICTURES).getAbsolutePath();// 在公共目录下创建…...
Ajax 揭秘:异步 Web 交互的艺术
Ajax 揭秘:异步 Web 交互的艺术 一 . Ajax 的概述1.1 什么是 Ajax ?1.2 同步和异步的区别1.3 Ajax 的应用场景1.3.1 注册表单的用户名异步校验1.3.2 内容自动补全 二 . Ajax 的交互模型和传统交互模型的区别三 . Ajax 异步请求 axios3.1 axios 介绍3.1.1 使用步骤3…...

TitleBar:打造高效Android标题栏的新选择
在Android应用开发中,标题栏是用户界面的重要组成部分。一个好的标题栏不仅能够提升应用的专业感,还能增强用户体验。然而,传统的标题栏实现方式往往存在代码冗余、样式不统一、性能开销大等问题。今天,我们将介绍一个名为TitleBa…...

Lua协同程序Coroutine
Lua 协同程序(Coroutine) 定义 Lua 协同程序(Coroutine)与线程类似:拥有独立的堆栈、局部变量、指令指针,同时又与其它协同程序共享全局变量和其它大部分东西。 协同程序可以理解为一种特殊的线程,可以暂停和恢复其执行,从而允…...

【vue+帆软】帆软升级,从版本9升级到版本11,记录升级过程
帆软要升级,记录下过程 1、帆软官网地址必不可少,戳这里,跳转帆软官网 点击前端开发指南 点击JS API 跳转过来就是版本11 一直往下翻,在最底部有个2.2 在Web中使用,圈起来的就是要引入到index.html中的脚本 在项…...

linux从0到1 基础完整知识
1. Linux系统概述 Linux是一种开源操作系统,与Windows或macOS等操作系统不同,Linux允许用户自由地查看、修改和分发其源代码。以下是Linux系统的一些显著的优势。 稳定性和可靠性: 内核以其稳定性而闻名,能够持续运行数月甚至数…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
