【C++二分查找】2517. 礼盒的最大甜蜜度
本文涉及的基础知识点
C++二分查找
贪心(决策包容性)
LeetCode 2517. 礼盒的最大甜蜜度
给你一个正整数数组 price ,其中 price[i] 表示第 i 类糖果的价格,另给你一个正整数 k 。
商店组合 k 类 不同 糖果打包成礼盒出售。礼盒的 甜蜜度 是礼盒中任意两种糖果 价格 绝对差的最小值。
返回礼盒的 最大 甜蜜度。
示例 1:
输入:price = [13,5,1,8,21,2], k = 3
输出:8
解释:选出价格分别为 [13,5,21] 的三类糖果。
礼盒的甜蜜度为 min(|13 - 5|, |13 - 21|, |5 - 21|) = min(8, 8, 16) = 8 。
可以证明能够取得的最大甜蜜度就是 8 。
示例 2:
输入:price = [1,3,1], k = 2
输出:2
解释:选出价格分别为 [1,3] 的两类糖果。
礼盒的甜蜜度为 min(|1 - 3|) = min(2) = 2 。
可以证明能够取得的最大甜蜜度就是 2 。
示例 3:
输入:price = [7,7,7,7], k = 2
输出:0
解释:从现有的糖果中任选两类糖果,甜蜜度都会是 0 。
提示:
2 <= k <= price.length <= 105
1 <= price[i] <= 109
C++ 二分查找+贪心
将price按升序排序。本题的Check函数f(x):是否存在某种方案甜蜜度大于等于x。 ⟺ \iff ⟺ price中任意选择k个元素,两两差的绝对值 >= x。
性质一:某合法方案如果不包括min(price),则将已选择的糖果价格最低的换成min(price),仍然合法。
性质二:如果选择的第i个,第i+1个糖果之间有价格>= 第i个糖果+x,则用此糖果换第i+1个糖果。
总结:选择min(price)后,按性质三选择,简称g(x)。
f(x) → \rightarrow →g(x) ;g(x)的方案符合题意,故g(x) → \rightarrow → f(x)。即f(x) ⟺ \iff ⟺ g(x)。
本题的解f(x)的最大解,即g(x)的最大解也是本题答案。
二分类型:寻找尾端。
Check函数的参数范围:[0,1e9]
代码
核心代码
template<class INDEX_TYPE>
class CBinarySearch
{
public:CBinarySearch(INDEX_TYPE iMinIndex, INDEX_TYPE iMaxIndex):m_iMin(iMinIndex),m_iMax(iMaxIndex) {}template<class _Pr>INDEX_TYPE FindFrist( _Pr pr){auto left = m_iMin - 1;auto rightInclue = m_iMax;while (rightInclue - left > 1){const auto mid = left + (rightInclue - left) / 2;if (pr(mid)){rightInclue = mid;}else{left = mid;}}return rightInclue;}template<class _Pr>INDEX_TYPE FindEnd( _Pr pr){int leftInclude = m_iMin;int right = m_iMax + 1;while (right - leftInclude > 1){const auto mid = leftInclude + (right - leftInclude) / 2;if (pr(mid)){leftInclude = mid;}else{right = mid;}}return leftInclude;}
protected:const INDEX_TYPE m_iMin, m_iMax;
};class Solution {public:int maximumTastiness(vector<int>& price, int k) {sort(price.begin(), price.end());auto Check = [&](int mid) {int pre = price.front();int cnt = k - 1;for (int i = 1; (i < price.size())&& cnt ; i++) {if (price[i] >= mid + pre) {cnt--;pre = price[i];}}return 0 == cnt;};return CBinarySearch<int>(0, 1e9).FindEnd(Check);}};
单元测试
vector<int> price;int k;TEST_METHOD(TestMethod1){price = { 1,1000'000'000 }, k = 2;auto res = Solution().maximumTastiness(price, k);AssertEx(999'999'999, res);}TEST_METHOD(TestMethod11){price = { 13, 5, 1, 8, 21, 2 }, k = 3;auto res = Solution().maximumTastiness(price, k);AssertEx(8, res);}TEST_METHOD(TestMethod12){price = { 1,3,1 }, k = 2;auto res = Solution().maximumTastiness(price, k);AssertEx(2, res);}TEST_METHOD(TestMethod13){price = { 7,7,7,7 }, k = 2;auto res = Solution().maximumTastiness(price, k);AssertEx(0, res);}

扩展阅读
| 我想对大家说的话 |
|---|
| 工作中遇到的问题,可以按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 学习算法:按章节学习《喜缺全书算法册》,大量的题目和测试用例,打包下载。重视操作 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
| 失败+反思=成功 成功+反思=成功 |
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【C++二分查找】2517. 礼盒的最大甜蜜度
本文涉及的基础知识点 C二分查找 贪心(决策包容性) LeetCode 2517. 礼盒的最大甜蜜度 给你一个正整数数组 price ,其中 price[i] 表示第 i 类糖果的价格,另给你一个正整数 k 。 商店组合 k 类 不同 糖果打包成礼盒出售。礼盒的 甜蜜度 是礼…...

【详解】数据库E-R图——医院计算机管理系统
题目 某医院病房计算机管理中需要如下信息: 科室:科室名,科室地址,科室电话,医生姓名 病房:病房号,床位号,所属科室名 医生:工作证号,姓名,性别&a…...

分类预测|基于改进的灰狼IGWO优化支持向量机SVM的数据分类预测matlab程序 改进策略:Cat混沌与高斯变异
分类预测|基于改进的灰狼IGWO优化支持向量机SVM的数据分类预测matlab程序 改进策略:Cat混沌与高斯变异 文章目录 一、基本原理原理流程1. **定义目标函数**2. **初始化GWO**3. **评估适应度**4. **更新狼的位置**5. **更新狼的等级**6. **重复迭代**7. **选择最佳解…...

圆锥曲线练习
设 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A\left( x_{1}, y_{1} \right), B\left( x_{2}, y_{2} \right) A(x1,y1),B(x2,y2) l : y k ( x 2 ) l: y k\left( x2 \right) l:yk(x2) 显然 y 0 y0 y0符合题意 当 k ≠ 0 k\neq 0 k0 联立 l l l和 C C C ( k 2 1 2 ) x…...

STM32时钟树
1 什么是时钟 2 时钟数简图...

NX—UI界面生成的文件在VS上的设置
UI界面保存生成的三个文件 打开VS创建项目,删除自动生成的cpp文件,将生成的hpp和cpp文件拷贝到项目的目录下,并且在VS项目中添加现有项目。 修改VS的输出路径,项目右键选择属性,链接器中的常规,文件路径D:…...

Wine容器内程序执行sh脚本问题研究
问题背景 wpf程序在wine环境执行sh脚本,不能等待脚本执行完成自动退出的问题进行了研究,需求很简单,在wpf程序使用cmd,或者bat ,又或者是直接执行sh脚本,想到脚本执行完成才处理后面的逻辑。但是实际验证过…...

《深度学习》OpenCV轮廓检测 模版匹配 解析及实现
目录 一、模型匹配 1、什么是模型匹配 2、步骤 1)提取模型的特征 2)在图像中查找特征点 3)进行特征匹配 4)模型匹配 3、参数及用法 1、用法 2、参数 1)image:待搜索对象 2)templ&am…...

Java XML
1、XML文件介绍 配置文件:用来保存设置的一些东西。 拿IDEA来举例,比如设置的背景图片,字体信息,字号信息和主题信息等等。 (1)以前是用txt保存的,没有任何优点,而且不利于阅读&a…...
好用的视频压缩工具有哪些?这4款千万不要错过
视频压缩的方法有很多种,像我们手机里的视频剪辑工具,手机和电脑自带的压缩功能,在线压缩网站,专业压缩软件压缩等等。不同的场景和需求下大家可以选择不同的工具,但是如果碰到需要大量和经常压缩视频的话,…...

【Python爬虫系列】_016.关于登录和验证码
我 的 个 人 主 页:👉👉 失心疯的个人主页 👈👈 入 门 教 程 推 荐 :👉👉 Python零基础入门教程合集 👈👈 虚 拟 环 境 搭 建 :👉&…...

基于opencv实现双目立体匹配点云距离
双目相机或两个单目相机。 一、相机标定 MATLAB软件,打开双目标定app。 点击add images,弹出加载图像的窗口,分别导入左图和右图,设置黑白格长度(标定板的长度一般为20)。 点击确定,弹出加载…...

RabbitMQ高级篇,进阶内容
强烈建议在看本篇博客之前快速浏览文章:RabbitMQ基础有这一篇就够了 RabbitMQ高级篇 0. 前言1. 发送者的可靠性1.1 生产者重试机制1.2 生产者确认机制1.3 实现生产者确认 2. MQ的可靠性2.1 MQ持久化2.2 LazyQueue 3. 消费者的可靠性3.1 消费者确认机制3.2 失败重试策…...

STM32重定义printf,实现串口打印
在“usart.c”文件中加入以下代码 #ifdef __GNUC__#define PUTCHAR_PROTOTYPE int __io_putchar(int ch) #else#define PUTCHAR_PROTOTYPE int fputc(int ch, FILE *f) #endifPUTCHAR_PROTOTYPE{HAL_UART_Transmit(&huart1 , (uint8_t *)&ch, 1, 0xFFFF);return ch; }…...

项目进度
变为负进度了,还是要用baseservlet,我就又重新写了一部分,看了好几遍视频,突然就想明白了,感觉每次要上课,就时间不连续思路总是断,今天晚自习算是搞懂了怎么写了,就是代码有点多&am…...

Android的内核
Android的内核是基于Linux的长期支持版本的“Android通用内核(ACK)”。 Android作为一个广泛使用的操作系统,其根基在于内核的设计和功能。下面将深入探讨Android内核的各个方面,从其基本结构到与Linux内核的关系,再到内核的版本管理及在设备…...

Github Wiki 超链接 转 码云Gitee Wiki 超链接
Github Wiki 超链接 转 码云Gitee Wiki 超链接 Github 是 :[[相对路径]] Gitee 是 :[链接文字](./相对路径) 查找:\[\[(.*?)\]\] 替换:[$1]\(./$1\) 或替换:**[$1]\(./$1\)** (码云的超链接,很…...

Android10源码刷入Pixel2以及整合GMS
一、ASOP源码下载 具体可以参考我之前发布的文章 二、下载相关驱动包 这一步很关键,关系到编译后的镜像能否刷入后运行 下载链接:Nexus 和 Pixel 设备的驱动程序二进制文件 如下图所示,将两个驱动程序上传到Ubuntu服务器,并进行解压,得到两个脚本: 下载解压后会有两…...
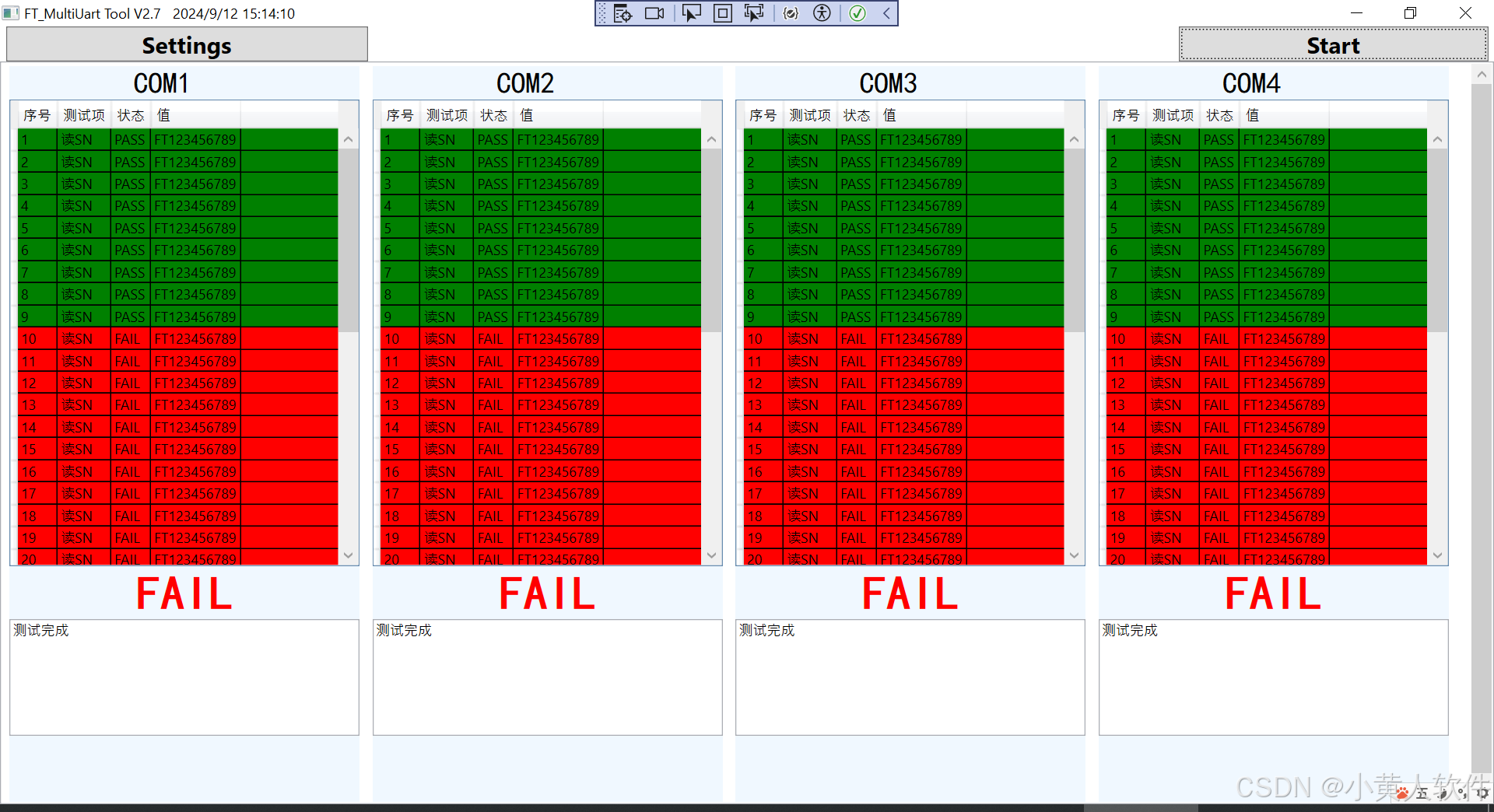
wpf触发与模板的使用示例:批量生产工具
批量生产工具 <Window x:Class"WpfM20UpdateFW.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schemas.microsoft.com/expressio…...

brew install node提示:Error: No such keg: /usr/local/Cellar/node
打开本地文件发现Cellar目录下无法生成 node文件,应该是下载时出现问题,重复下载无法解决问题,只能重新安装brew。 步骤1(安装 brew): /bin/zsh -c “$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/ra…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
