量化投资策略_因子打分选股的案例实现
一:因子打分选股的介绍
因子打分选股是一种量化投资策略,它通过选取多个与股票收益率相关的因子,对股票进行综合评分,然后根据评分来选择股票构建投资组合。以下是构建多因子打分选股模型的一般步骤:
数据预处理:首先,需要准备好待检验的原始因子池及其数据,并进行初步整理。这包括基础数据采集,归纳不同风格的因子种类,并确定因子的计算方法。例如,估值因子、波动率因子和杠杆因子等 。
因子有效性检验:通过实证分析,筛选掉与收益率相关性不高的因子,得到有效的因子池。这通常涉及特征分析、中性化处理(市值和行业分析)、回归法分析和IC法辅助分析等步骤 。
大类因子合成:在筛选出有效因子后,需要对因子进行合成,以减少多重共线性的影响,并提高模型的稳定性。这可能包括细分因子间相关性分析、同种因子下的细分因子合成和合成因子间相关性检验 。
构造模型:确定各因子的权重,可以通过等权处理、因子IC均值加权、IR_IC法加权或最大化复合因子IR等方法来实现。然后,根据权重对个股进行打分,并筛选出评分高的股票 。
组合优化:在得到基础数据后,可能需要对模型进行优化,以避免风险过多地暴露在某一行业或因子上。这可以通过添加约束条件和使用二次规划求解权重来实现 。
模型评估与持续改进:最后,需要对模型进行评估,包括回测和绩效分析,以确保模型的有效性。同时,模型需要定期进行验证和更新,以适应市场的变化 。
二:因子打分选股的思路解释
由于因子打分选股包含的内容较多,为了演示因子打分选股的思路,下面来演示一个因子打分选股的简单实例。具体来说可以分为以下几个步骤:
选择因子:首先需要确定用于打分的因子。这些因子通常与股票的表现相关,例如市盈率、市净率、股息率、盈利增长率等。
数据收集:收集相关股票的历史数据,包括价格、市值、财务指标等。
因子处理:对每个因子进行标准化或归一化处理,以确保它们在同一尺度上。
打分模型:设计一个模型来综合这些因子,为每只股票打分。这可以是一个简单的加权平均模型,也可以是更复杂的机器学习模型。
选股策略:根据打分结果,选择分数最高的股票进行投资。
回测与优化:对选股策略进行历史数据回测,以评估其表现,并根据结果对策略进行优化。
实施与监控:将策略应用于实际交易,并持续监控其表现,必要时进行调整。
现在将使用Python来模拟这个过程。例如,我们可以选择几个常见的财务指标作为因子,使用简单的加权平均方法来计算股票的得分。
我们将使用以下三个因子:
- 市盈率(PE)
- 市净率(PB)
- 股息率(Dividend Yield)
import pandas as pd
import numpy as np# 示例数据
data = {'股票': ['股票A', '股票B', '股票C'],'市盈率': [10, 15, 12],'市净率': [1.5, 1.2, 1.8],'股息率': [2.5, 1.8, 2.0] # 假设以百分比表示
}# 创建DataFrame
df = pd.DataFrame(data)df模拟的示例数据如下:

我们将为每只股票计算一个简单的加权总分,其中每个因子的权重相等。
# 因子打分
# 这里我们简单地使用每个因子的倒数作为得分,因为通常我们认为市盈率低、市净率低、股息率高的股票更好
# 实际应用中,可能需要更复杂的标准化方法
df['市盈率得分'] = 1 / df['市盈率']
df['市净率得分'] = 1 / df['市净率']
df['股息率得分'] = df['股息率']# 计算总得分
df['总分'] = df[['市盈率得分', '市净率得分', '股息率得分']].mean(axis=1)df.sort_values(by='总分', ascending=False) # 按总分降序排列
排序结果如下:

根据我们的简单模型,股票A在三个因子上的表现最好,因此得分最高。这个模型只是一个示例,实际中可能需要考虑更多的因子和更复杂的权重分配方法,还需考虑市场趋势、行业特性、公司基本面分析等其他重要因素。
三:每日股票行情数据

如果想了解更多相关金融工程的内容,可以关注之前的内容。
相关文章:

量化投资策略_因子打分选股的案例实现
一:因子打分选股的介绍 因子打分选股是一种量化投资策略,它通过选取多个与股票收益率相关的因子,对股票进行综合评分,然后根据评分来选择股票构建投资组合。以下是构建多因子打分选股模型的一般步骤: 数据预处理&…...

架构师知识梳理(七):软件工程-工程管理与开发模型
软件工程概述 软件开发生命周期 软件定义时期:包括可行性研究和详细需求分析过程,任务是确定软件开发工程必须完成的总目标,具体可分成问题定义、可行性研究、需求分析等。软件开发时期:就是软件的设计与实现,可分成…...

bp的模块被隐藏了
看我们现在没有代理那个模块了 我们点击查看 这里有被我们隐藏的模块,比如代理等,把前面的眼睛点一下 这个模块就出来了,如果想把他固定在任务栏里 拖动这个位置 就好了,如果有其他问题可以留言,看到可进我的努力给你…...
)
C++学习笔记(21)
243、条件变量-生产消费者模型 条件变量是一种线程同步机制。当条件不满足时,相关线程被一直阻塞,直到某种条件出现,这些线 程才会被唤醒。 C11 的条件变量提供了两个类: condition_variable:只支持与普通 mutex 搭配&…...

Ubuntu系统入门指南:常用命令详解
Ubuntu系统入门指南:常用命令详解 引言 Ubuntu是一个基于Linux内核的开源操作系统,由Canonical公司和社区共同开发和维护。它以易用性、稳定性和广泛的软件支持而著称,广泛应用于个人电脑、服务器和云计算环境。对于新手来说,掌…...

keep-alive缓存不了iframe
最近做了个项目,其中有个页面是由 iframe 嵌套了一个另外的页面,在运行的过程中发现 KeepAlive 并不生效,每次切换路由都会触发 iframe 页面的重新渲染,代码如下: <router-view v-slot"{ Component }">…...
Gradio快速部署构建AIGC的web应用 ,python
Gradio快速部署构建AIGC的web应用 ,python Gradio开源项目链接: https://github.com/gradio-app/gradiohttps://github.com/gradio-app/gradio (1)python的pip安装: pip install gradio (2)写…...

《职教论坛》
《职教论坛》投稿须知 《职教论坛》为全国中文核心期刊。为进一步提高期刊的规范化和标准化,也可使作者投搞有规可循,特对来稿提出如下要求: 一、稿件应有创新内容,应观点明确、资料准确、结构严谨、表述清楚、文字简明ÿ…...

JZ2440开发板——S3C2440的时钟体系
参考博客 (1)S3C2440-裸机篇-05 | S3C2440时钟体系详解(FCLK、PCLK、HCLK) 一、三种时钟(FCLK、HCLK、PCLK) 如下图所示,S3C2440的时钟控制逻辑,给整个芯片提供三种时钟࿱…...

[数据集][目标检测]男女性别检测数据集VOC+YOLO格式9769张2类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):9769 标注数量(xml文件个数):9769 标注数量(txt文件个数):9769 标注…...

static 初始化报错
在 C 或 C 中,当你在函数中使用 static 关键字初始化一个局部变量时,编译器要求初始化器(initializer)是编译时常量。如果你尝试用动态计算的值初始化 static 变量(如函数参数或运行时生成的值),…...

3D Gaussian Splatting 论文学习
概述 目前比较常见的渲染方法大致可以分为2种: 将场景中的物体投影到渲染平面:传统的渲染管线就是这种方式,主要针对Mesh数据,可以将顶点直接投影成2D的形式,配合光栅化、深度测试、Alpha混合等就可以得到渲染的图像…...
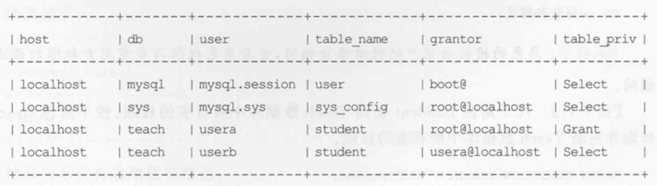
MySQL 安全机制全面解析
在如今的数字化时代,数据库安全 变得越来越重要。为了防止对数据库进行非法操作,MySQL 定义了一套完整的安全机制,包括用户管理、权限管理 和 角色管理。本文将为你深入浅出地介绍这三大安全机制,帮助你轻松掌握MySQL的安全管…...
研究new Vue()中的 initProvide)
vue原理分析(十四)研究new Vue()中的 initProvide
在Vue.prototype._init 中有一些init函数,今天我们来研究这些init函数 Vue.prototype._init function (options) {......{initProxy(vm);}......initLifecycle(vm);initEvents(vm);initRender(vm);callHook$1(vm, beforeCreate, undefined, false /* setContext *…...

Qt控制开发板的LED
Qt控制开发板的LED 使用开发板的IO接口进行控制是嵌入式中非常重要的一点,就像冯诺依曼原理说的一样,一个计算机最起码要有输入输出吧,我们有了信息的接收和处理,那我们就要有输出。 我们在开发板上一般都是使用开发板的GPIO接口…...

S3C2440开发板点亮LED灯+PWM定时器
目录 GPIO引脚和寄存器概述 点亮LED灯步骤 1.配置GPIO 2.点亮LED 设置引脚为输出 控制引脚电平 完整代码 PWM GPIO引脚和寄存器概述 GPIO端口: S3C2440的GPIO引脚可被配置为输入或输出(控制LED的引脚通常配置为输出模式)。寄存器&#…...

S-Procedure的基本形式及使用
理论 Lemma 1. ( S- Procedure[ 34] ) : Define the quadratic func- \textbf{Lemma 1. ( S- Procedure[ 34] ) : Define the quadratic func- } Lemma 1. ( S- Procedure[ 34] ) : Define the quadratic func- tions w.r.t. x ∈ C M 1 \mathbf{x}\in\mathbb{C}^M\times1 x…...

free -h 查看内存free空间不足
free空间不足 大部分被buff/cache占用 解决办法一: 手动释放缓存 释放页缓存 sudo sync; sudo sysctl -w vm.drop_caches1 释放目录项和inode缓存 sudo sync; sudo sysctl -w vm.drop_caches2 释放所有缓存(页缓存、目录项和inode缓存) sudo sync…...

rust学习笔记
参考资料:https://doc.rust-lang.org/book/ch01-02-hello-world.html 一、 编译与运行 在 Rust 中,编译和运行代码的常用命令是使用 cargo,这是 Rust 的包管理和构建工具。以下是使用 cargo 和 rustc(Rust 编译器)的具…...

【有啥问啥】复习变分下界即证据下界(Evidence Lower Bound, ELBO):原理与应用
复习变分下界即证据下界(Evidence Lower Bound, ELBO):原理与应用 变分下界(Variational Lower Bound),也称为“证据下界”(Evidence Lower Bound, ELBO),是概率模型中的…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
