数学基础 -- 线性代数之奇异值
奇异值与其应用
1. 奇异值定义
对于任意的矩阵 A A A(可以是方阵或非方阵),存在三个矩阵 U U U、 Σ \Sigma Σ 和 V V V,使得:
A = U Σ V T A = U \Sigma V^T A=UΣVT
其中:
- U U U 是一个 m × m m \times m m×m 的正交矩阵,表示左奇异向量;
- V V V 是一个 n × n n \times n n×n 的正交矩阵,表示右奇异向量;
- Σ \Sigma Σ 是一个 m × n m \times n m×n 的对角矩阵,其中对角线上的元素为奇异值。
2. 奇异值的性质
- 非负性:奇异值始终为非负数,即对角矩阵 Σ \Sigma Σ 的对角元素均为非负。
- 奇异值的数量:对于一个 m × n m \times n m×n 的矩阵 A A A,最多有 min ( m , n ) \min(m, n) min(m,n) 个奇异值。
- 矩阵的秩:矩阵 A A A 的秩等于其非零奇异值的数量。
- 特征值与奇异值的关系:方阵 A A A 的奇异值是矩阵 A T A A^T A ATA 的特征值的平方根。
- 不变性:奇异值是矩阵的固有属性,与矩阵的旋转或变换无关。
2.1 奇异值分解的示例
为了更好地理解奇异值分解的具体过程和应用,我们通过一个简单的例子展示如何进行奇异值分解。
示例矩阵
考虑一个 3 × 2 3 \times 2 3×2 的矩阵 A A A:
A = ( 1 0 0 1 1 1 ) A = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{pmatrix} A= 101011
我们将对这个矩阵进行奇异值分解。
1. 计算 A T A A^T A ATA
首先,我们计算矩阵 A T A A^T A ATA:
A T A = ( 1 0 1 0 1 1 ) ( 1 0 0 1 1 1 ) = ( 2 1 1 2 ) A^T A = \begin{pmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{pmatrix} = \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} ATA=(100111) 101011 =(2112)
2. 求 A T A A^T A ATA 的特征值和特征向量
接下来,我们求矩阵 A T A A^T A ATA 的特征值和特征向量。先写出特征方程:
det ( A T A − λ I ) = det ( 2 − λ 1 1 2 − λ ) = ( 2 − λ ) 2 − 1 = λ 2 − 4 λ + 3 = 0 \det(A^T A - \lambda I) = \det\begin{pmatrix} 2 - \lambda & 1 \\ 1 & 2 - \lambda \end{pmatrix} = (2 - \lambda)^2 - 1 = \lambda^2 - 4\lambda + 3 = 0 det(ATA−λI)=det(2−λ112−λ)=(2−λ)2−1=λ2−4λ+3=0
解得特征值为:
λ 1 = 3 , λ 2 = 1 \lambda_1 = 3, \quad \lambda_2 = 1 λ1=3,λ2=1
对于 λ 1 = 3 \lambda_1 = 3 λ1=3,解特征方程 ( A T A − 3 I ) v = 0 (A^T A - 3I)v = 0 (ATA−3I)v=0 得到特征向量:
v 1 = 1 2 ( 1 1 ) v_1 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} v1=21(11)
对于 λ 2 = 1 \lambda_2 = 1 λ2=1,解 ( A T A − I ) v = 0 (A^T A - I)v = 0 (ATA−I)v=0 得到特征向量:
v 2 = 1 2 ( 1 − 1 ) v_2 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ -1 \end{pmatrix} v2=21(1−1)
因此,矩阵 V V V 的列向量是特征向量:
V = ( 1 2 1 2 1 2 − 1 2 ) V = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} V=(212121−21)
3. 计算奇异值
奇异值是 A T A A^T A ATA 的特征值的平方根,因此:
σ 1 = 3 , σ 2 = 1 = 1 \sigma_1 = \sqrt{3}, \quad \sigma_2 = \sqrt{1} = 1 σ1=3,σ2=1=1
因此,矩阵 Σ \Sigma Σ 为:
Σ = ( 3 0 0 1 0 0 ) \Sigma = \begin{pmatrix} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \end{pmatrix} Σ= 300010
4. 计算 U U U
矩阵 U U U 的列向量是矩阵 A A A 的左奇异向量,左奇异向量通过公式 A v i = σ i u i A v_i = \sigma_i u_i Avi=σiui 计算。
对于 σ 1 = 3 \sigma_1 = \sqrt{3} σ1=3,我们有:
A ( 1 2 1 2 ) = ( 1 1 2 ) , u 1 = 1 6 ( 1 1 2 ) A \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}, \quad u_1 = \frac{1}{\sqrt{6}} \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} A(2121)= 112 ,u1=61 112
对于 σ 2 = 1 \sigma_2 = 1 σ2=1,我们有:
A ( 1 2 − 1 2 ) = ( 1 − 1 0 ) , u 2 = 1 2 ( 1 − 1 0 ) A \begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}, \quad u_2 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} A(21−21)= 1−10 ,u2=21 1−10
因此,矩阵 U U U 为:
U = ( 1 6 1 2 1 6 − 1 2 2 6 0 ) U = \begin{pmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} \\ \frac{2}{\sqrt{6}} & 0 \end{pmatrix} U= 61616221−210
5. 奇异值分解结果
最终,矩阵 A A A 的奇异值分解为:
A = U Σ V T A = U \Sigma V^T A=UΣVT
其中:
U = ( 1 6 1 2 1 6 − 1 2 2 6 0 ) , Σ = ( 3 0 0 1 0 0 ) , V T = ( 1 2 1 2 1 2 − 1 2 ) U = \begin{pmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} \\ \frac{2}{\sqrt{6}} & 0 \end{pmatrix}, \quad \Sigma = \begin{pmatrix} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \end{pmatrix}, \quad V^T = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} U= 61616221−210 ,Σ= 300010 ,VT=(212121−21)
3. 奇异值分解的应用
3.1 数据降维与压缩
奇异值分解可用于数据降维,特别是在图像处理或主成分分析(PCA)中,通过保留最大的奇异值,能够有效减少数据量,同时保留数据的主要信息。
3.2 最小二乘问题
在解超定方程或病态方程时,奇异值分解能够提供稳定的最小二乘解。通过分解矩阵 A A A 为奇异值分解形式 A = U Σ V T A = U \Sigma V^T A=UΣVT,我们可以稳定地求解方程组。
例子:奇异值分解在数据压缩中的应用
1. 问题描述
假设我们有一张大小为 100 × 100 100 \times 100 100×100 的灰度图像,用一个矩阵 A A A 表示,每个元素表示像素的亮度值。我们希望通过奇异值分解对这张图像进行压缩。
2. 奇异值分解
对矩阵 A A A 进行奇异值分解,得到:
A = U Σ V T A = U \Sigma V^T A=UΣVT
其中:
- U U U 是 100 × 100 100 \times 100 100×100 的矩阵;
- Σ \Sigma Σ 是 100 × 100 100 \times 100 100×100 的对角矩阵,包含奇异值;
- V T V^T VT 是 100 × 100 100 \times 100 100×100 的矩阵。
3. 压缩过程
我们只保留最大的 k = 20 k = 20 k=20 个奇异值,构造近似矩阵 A k A_k Ak:
A k = U k Σ k V k T A_k = U_k \Sigma_k V_k^T Ak=UkΣkVkT
其中:
- U k U_k Uk 是 100 × 20 100 \times 20 100×20 的矩阵;
- Σ k \Sigma_k Σk 是 20 × 20 20 \times 20 20×20 的对角矩阵;
- V k T V_k^T VkT 是 20 × 100 20 \times 100 20×100 的矩阵。
经过压缩后,总数据量从原来的 10,000 个数据点减少到 6400 个数据点。
例子:奇异值分解在最小二乘问题中的应用
1. 问题描述
我们要解一个线性方程组:
A x = b A x = b Ax=b
其中 A A A 是一个 3 × 2 3 \times 2 3×2 的矩阵, b b b 是一个 3 × 1 3 \times 1 3×1 的已知向量。
矩阵 A A A 和向量 b b b 如下:
A = ( 1 0 0 1 1 1 ) , b = ( 2 2 4 ) A = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{pmatrix}, \quad b = \begin{pmatrix} 2 \\ 2 \\ 4 \end{pmatrix} A= 101011 ,b= 224
2. 奇异值分解求解最小二乘问题
我们首先对 A A A 进行奇异值分解:
A = U Σ V T A = U \Sigma V^T A=UΣVT
通过计算得到:
U = ( − 0.577 0.707 − 0.577 − 0.707 − 0.577 0.000 ) , Σ = ( 1.732 0 0 1 ) , V T = ( − 0.707 − 0.707 0.707 − 0.707 ) U = \begin{pmatrix} -0.577 & 0.707 \\ -0.577 & -0.707 \\ -0.577 & 0.000 \end{pmatrix}, \quad \Sigma = \begin{pmatrix} 1.732 & 0 \\ 0 & 1 \end{pmatrix}, \quad V^T = \begin{pmatrix} -0.707 & -0.707 \\ 0.707 & -0.707 \end{pmatrix} U= −0.577−0.577−0.5770.707−0.7070.000 ,Σ=(1.732001),VT=(−0.7070.707−0.707−0.707)
2.1 计算 U T b U^T b UTb
U T b = ( − 0.577 − 0.577 − 0.577 0.707 − 0.707 0 ) ( 2 2 4 ) = ( − 4.618 1.414 ) U^T b = \begin{pmatrix} -0.577 & -0.577 & -0.577 \\ 0.707 & -0.707 & 0 \end{pmatrix} \begin{pmatrix} 2 \\ 2 \\ 4 \end{pmatrix} = \begin{pmatrix} -4.618 \\ 1.414 \end{pmatrix} UTb=(−0.5770.707−0.577−0.707−0.5770) 224 =(−4.6181.414)
2.2 解 Σ y = U T b \Sigma y = U^T b Σy=UTb
Σ y = ( 1.732 0 0 1 ) ( y 1 y 2 ) = ( − 4.618 1.414 ) \Sigma y = \begin{pmatrix} 1.732 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \begin{pmatrix} -4.618 \\ 1.414 \end{pmatrix} Σy=(1.732001)(y1y2)=(−4.6181.414)
解得:
y 1 = − 2.666 , y 2 = 1.414 y_1 = -2.666, \quad y_2 = 1.414 y1=−2.666,y2=1.414
2.3 计算 x = V y x = V y x=Vy
x = V y = ( − 0.707 − 0.707 0.707 − 0.707 ) ( − 2.666 1.414 ) = ( 2 1 ) x = V y = \begin{pmatrix} -0.707 & -0.707 \\ 0.707 & -0.707 \end{pmatrix} \begin{pmatrix} -2.666 \\ 1.414 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} x=Vy=(−0.7070.707−0.707−0.707)(−2.6661.414)=(21)
因此,最小二乘解为 x = ( 2 1 ) x = \begin{pmatrix} 2 \\ 1 \end{pmatrix} x=(21)。
总结
奇异值分解在数据压缩和最小二乘问题中有广泛的应用。在数据压缩中,通过保留最大的奇异值,我们可以有效减少数据量,压缩图片或信号;在最小二乘问题中,SVD 提供了数值稳定的解法,特别适用于病态或超定方程组。
相关文章:

数学基础 -- 线性代数之奇异值
奇异值与其应用 1. 奇异值定义 对于任意的矩阵 A A A(可以是方阵或非方阵),存在三个矩阵 U U U、 Σ \Sigma Σ 和 V V V,使得: A U Σ V T A U \Sigma V^T AUΣVT 其中: U U U 是一个 m m m \ti…...
Python爬虫使用实例-wallpaper
1/ 排雷避坑 🥝 中文乱码问题 print(requests.get(urlurl,headersheaders).text)出现中文乱码 原因分析: <meta charset"gbk" />解决方法: 法一: response requests.get(urlurl,headersheaders) response.en…...

探索Go语言中的随机数生成、矩阵运算与数独验证
1. Go中的随机数生成 在许多编程任务中,随机数的生成是不可或缺的。Go语言通过 math/rand 包提供了伪随机数生成方式。伪随机数由种子(seed)决定,如果种子相同,生成的数列也会相同。为了确保每次程序运行时产生不同的随机数,我们…...

无线安全(WiFi)
免责声明:本文仅做分享!!! 目录 WEP简介 WPA简介 安全类型 密钥交换 PMK PTK 4次握手 WPA攻击原理 网卡选购 攻击姿态 1-暴力破解 脚本工具 字典 2-Airgeddon 破解 3-KRACK漏洞 4-Rough AP 攻击 5-wifi钓鱼 6-wifite 其他 WEP简介 WEP是WiredEquivalentPri…...
)
牛客练习赛128:Cidoai的平均数对(背包dp)
题目描述 给定 nnn 对数 (ai,bi)(a_i,b_i)(ai,bi) 和参数 kkk,你需要选出一些对使得在满足 bib_ibi 的平均值不超过 kkk 的同时,aia_iai 的和最大,求出这个最大值。 输入描述: 第一行两个整数分别表示 n,kn,kn,k。 接下来 nnn 行&…...

Python世界:简易地址簿增删查改算法实践
Python世界:简易地址簿增删查改算法实践 任务背景编码思路代码实现本文小结 任务背景 该任务来自简明Python教程中迈出下一步一章的问题: 编写一款你自己的命令行地址簿程序, 你可以用它浏览、 添加、 编辑、 删除或搜索你的联系人ÿ…...
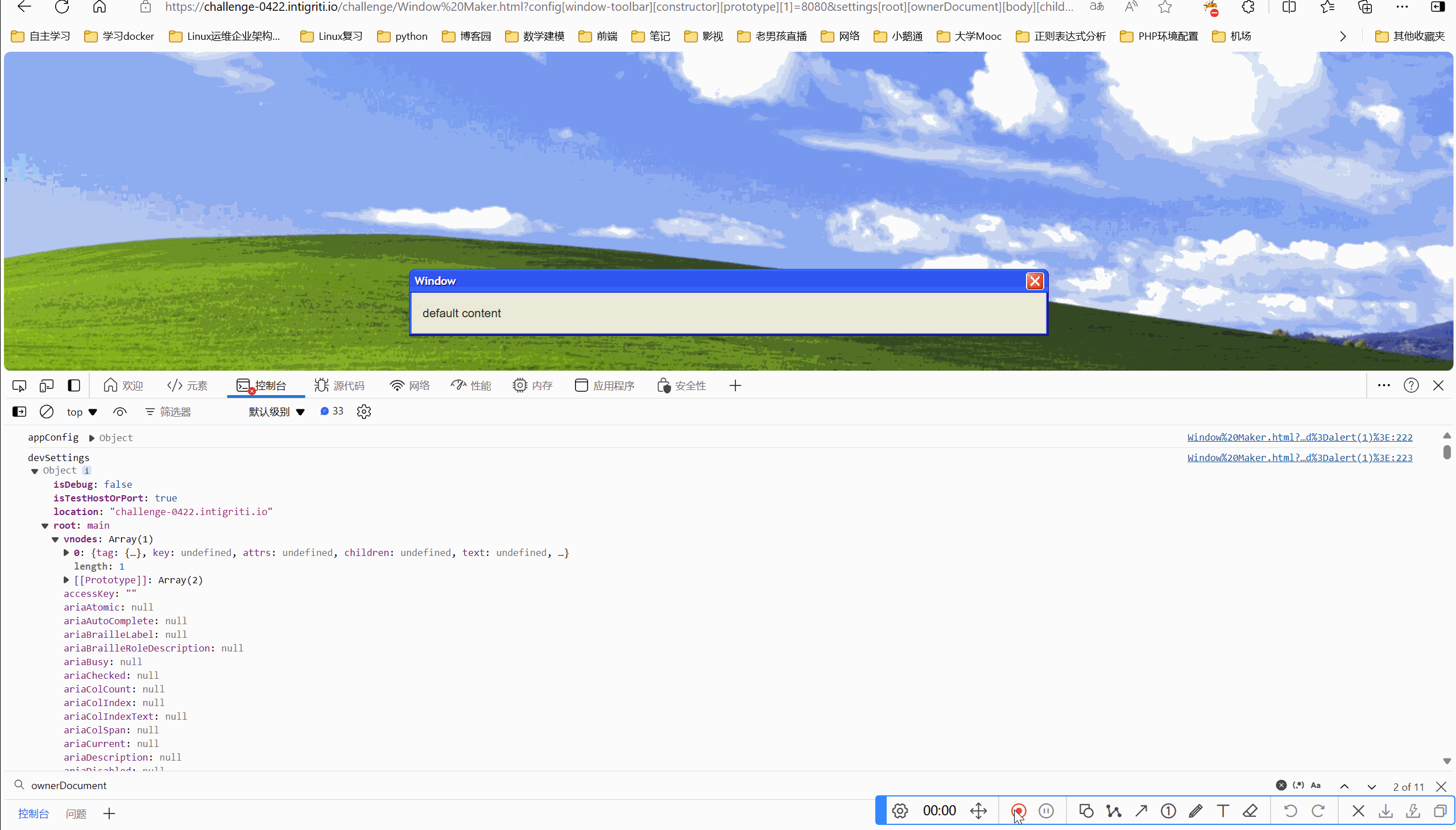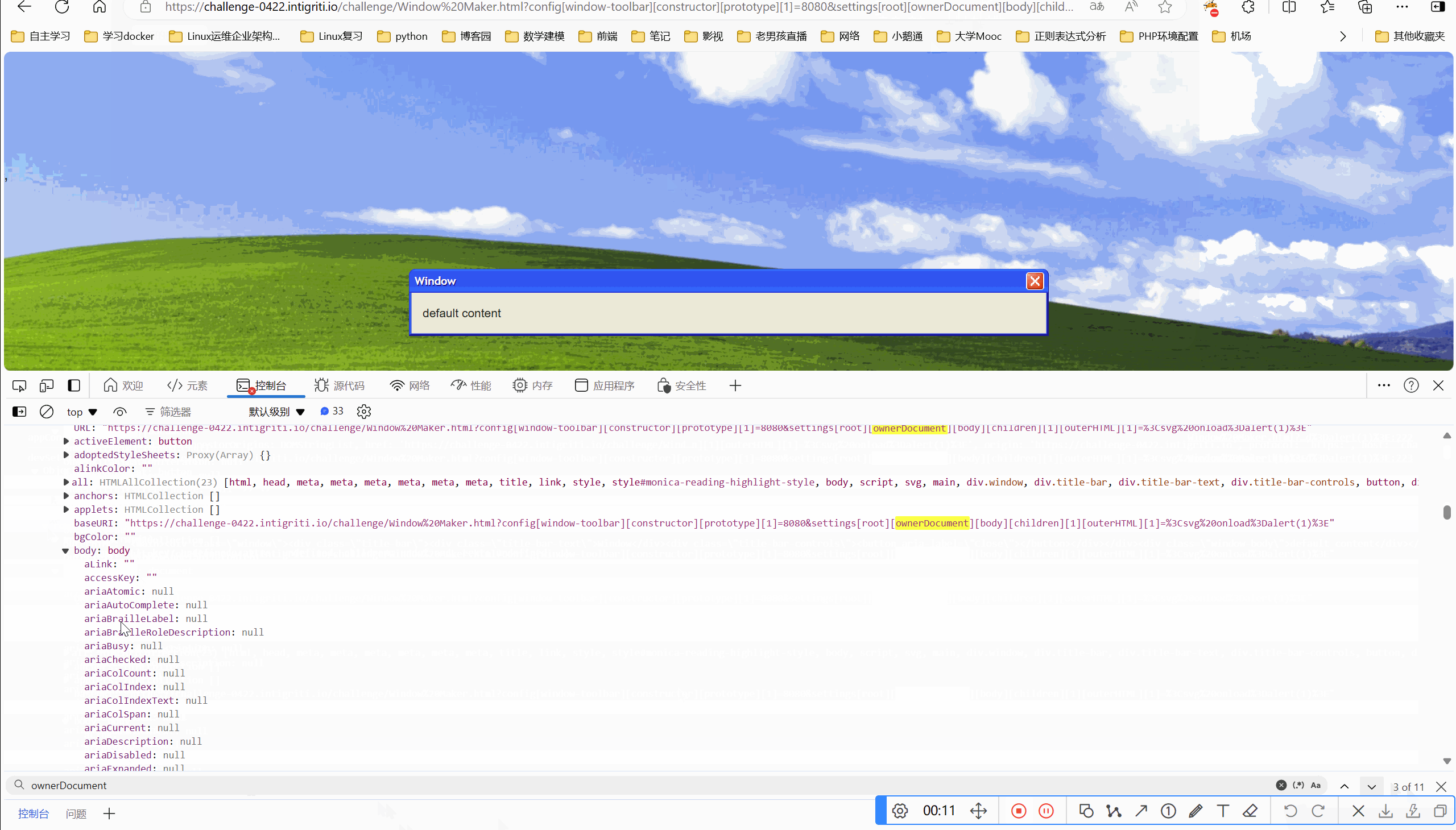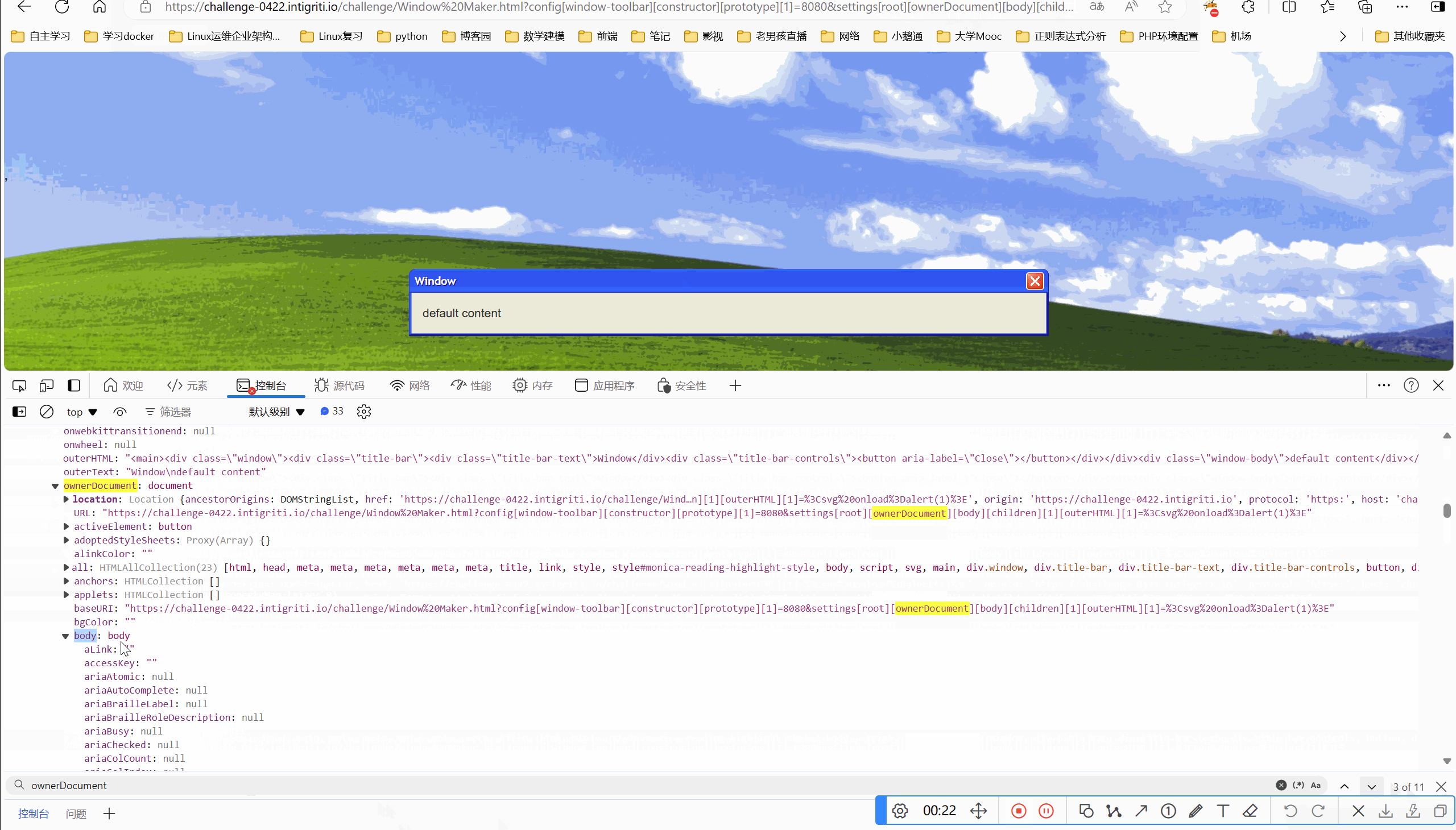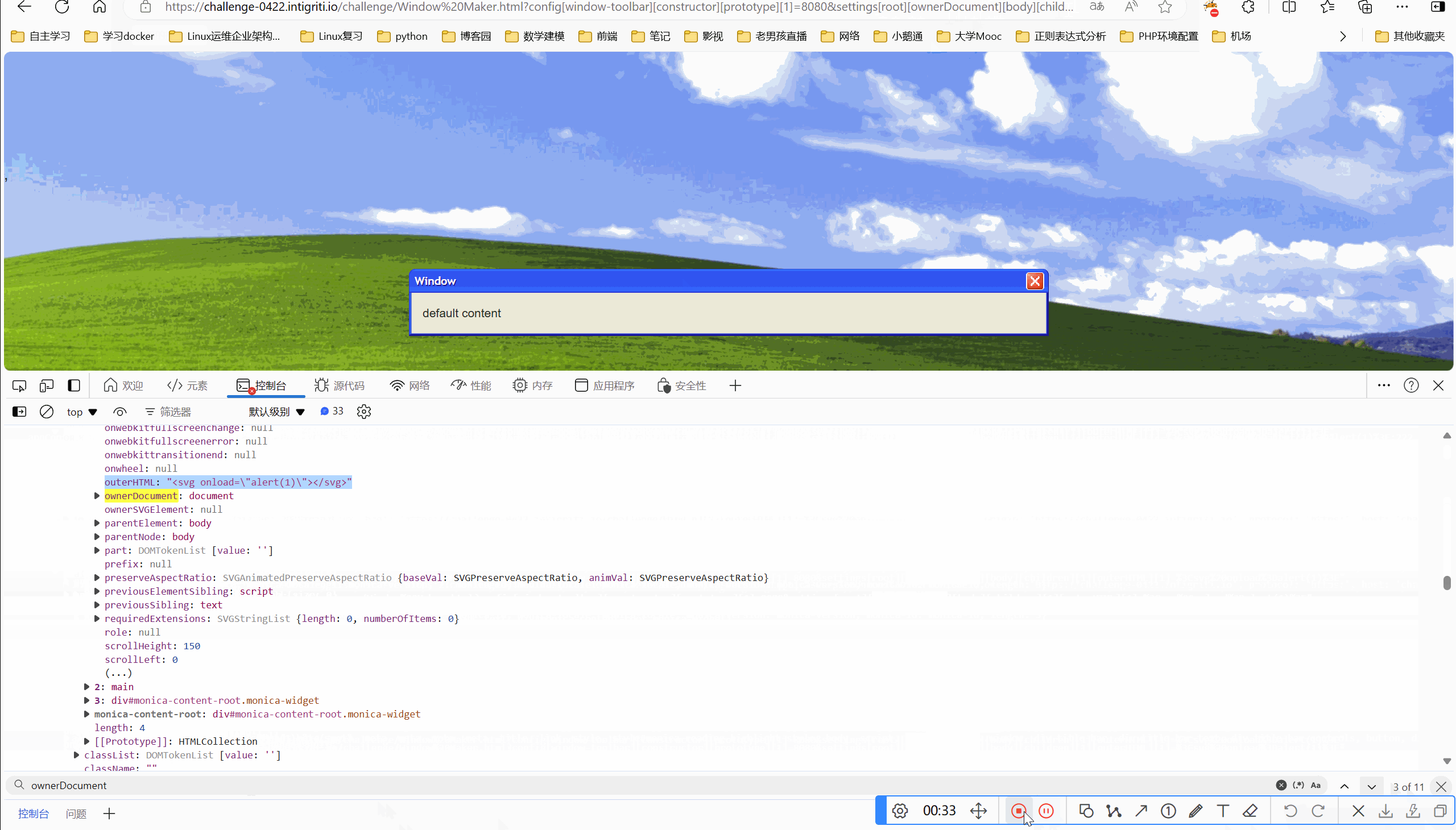
网络安全-intigriti-0422-XSS-Challenge Write-up
目录 一、环境 二、解题 2.1看源码 一、环境 Intigriti April Challenge 二、解题 要求:弹出域名就算成功 2.1看源码 我们看到marge方法,肯定是原型链污染题目 接的是传参,我们可控的点在于qs.config和qs.settings,这两个可…...

Debian Linux 11 使用crash
文章目录 前言一、环境安装1.1 安装debug package1.2 安装crash 二、使用crash 前言 # cat /etc/os-release PRETTY_NAME"Debian GNU/Linux 11 (bullseye)" NAME"Debian GNU/Linux" VERSION_ID"11" VERSION"11 (bullseye)" VERSION_C…...

python列表 — 按顺序找出b表中比a表多出的元素
目录 一、功能描述 二、适用场景 三、代码实现 一、功能描述 有a、b两个列表,a列表有3个元素;b列表有7个元素。b列表多出的一个元素可能在随机的位置,在不影响其他元素的情况下,找到b列表多出的那四个元素,并按照在…...

如何使用Python创建目录或文件路径列表
在 Python 中,创建目录或生成文件路径列表通常涉及使用 os、os.path 或 pathlib 模块。下面是一些常见的任务和方法,用于在 Python 中创建目录或获取文件路径列表。 问题背景 在初始阶段的 Python 学习过程中,可能遇到这样的问题:…...

领夹麦克风哪个品牌好,哪种领夹麦性价比高,无线麦克风推荐
在音频录制需求日益多样化的今天,无线领夹麦克风作为提升音质的关键设备,其重要性不言而喻。市场上鱼龙混杂,假冒伪劣、以次充好的现象屡见不鲜。这些产品往往以低价吸引消费者,却在音质、稳定性、耐用性等方面大打折扣࿰…...
)
苍穹外卖学习笔记(五)
文章目录 二.新增菜品1.图片上传2.具体新增菜品 二.新增菜品 1.图片上传 这里采用了阿里云oss对象存储服务 application.yml alioss:endpoint: ${sky.alioss.endpoint}access-key-id: ${sky.alioss.access-key-id}access-key-secret: ${sky.alioss.access-key-secret}bucket…...

什么是卷积层、池化层、BN层,有什么作用?
什么是卷积层、池化层、BN层,有什么作用? 卷积层池化层BN层 卷积层 定义: 卷积层是CNN中的核心组件,它通过卷积运算对输入数据进行特征提取。卷积层由多个卷积单元组成,每个卷积单元的参数通过反向传播算法优化得到。…...

[学习笔记]《CSAPP》深入理解计算机系统 - Chapter 4 处理器体系结构Chapter 5 优化程序性能
总结一些第四章和第五章的一些关键信息 Chapter 4 处理器体系结构将处理组织成阶段 Chapter 5 优化程序性能 Chapter 4 处理器体系结构 在硬件中,寄存器直接将它的输入和输出线连接到电路的其他盆。 在机器级变成中,寄存器代表的是 CPU 中为数不多的可寻…...

案例分享|我是这样转型做数据产品经理的?
本文为才聚学员投稿的原创作品,现在才聚正面向专业项目管理者征集“项目管理实战案例”原创文章,被采纳即可获得丰厚稿酬,欢迎大家关注公众号踊跃投稿。 如您有意向投稿,可将稿件投递给我们。 故事介绍 三段故事,讲…...

ffmpeg面向对象-rtsp拉流相关对象
目录 1.AVFormatContext和FFFormatContext类。1.1 概述1.2 构造函数1.3 oopc的继承实现 2. AVInputFormat 类。2.1 多态的实现 3.所用设计模式3.1模板模式3.2 工厂模式? 3.3 rtsp拉流建链 4.this指针5.小结6.rtsp拉流流程 1.AVFormatContext和FFFormatContext类。 …...

feign client发送Post请求,发送对象参数,服务端接收不到正确参数报错排查
记一次feignclient发送请求服务端接收不到正确参数排查 服务端代码: Operation(summary "Create team")PostMapping("post")RequiresPermissions("team:add")public RestResponse addTeam(Valid Team team) {this.teamService.crea…...

Hadoop林子雨安装
文章目录 hadoop安装教程注意事项: hadoop安装教程 链接: 安装教程 注意事项: 可以先安装ububtu增强功能,完成共享粘贴板和共享文件夹 ubuntu增强功能 2.这里就可以使用共享文件夹 或者在虚拟机浏览器,用 微信文件传输助手 传文…...
Springboot项目总结
1.为了调用写在其他包里面的类的方法 但是不使用new来实现调用这个类里面的方法,这个时候我们就需要将这个类注入到ioc容器里面,通过ioc容器来实现自动生成一个对象。 对ioc容器的理解:自动将一个对象实现new. 考察了and 和 or组合使用&…...

目标检测从入门到精通——数据增强方法总结
以下是YOLO系列算法(从YOLOv1到YOLOv7)中使用的数据增强方法的总结,包括每种方法的数学原理、相关论文以及对应的YOLO版本。 YOLO系列数据增强方法总结 数据增强方法数学原理相关论文图像缩放将输入图像缩放到固定大小(如448x44…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

Linux中INADDR_ANY详解
在Linux网络编程中,INADDR_ANY 是一个特殊的IPv4地址常量(定义在 <netinet/in.h> 头文件中),用于表示绑定到所有可用网络接口的地址。它是服务器程序中的常见用法,允许套接字监听所有本地IP地址上的连接请求。 关…...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...
