性能测试-性能分析与调优原理总结
 性能分析与调优如何下手,先从硬件开始,还是先从代码或数据库。 从操作系统(CPU调度,内存管理,进程调度,磁盘I/O)、网络、协议(HTTP, TCP/IP ),还是从应用程序代码,数据库调优,中间件配置等方面入手。
性能分析与调优如何下手,先从硬件开始,还是先从代码或数据库。 从操作系统(CPU调度,内存管理,进程调度,磁盘I/O)、网络、协议(HTTP, TCP/IP ),还是从应用程序代码,数据库调优,中间件配置等方面入手。
单一个中间件又分web中间件(apache 、IIS),应用中间件(tomcat 、weblogic 、webSphere )等。
虽然都是中间件,每一样拎出来往深了学都不是一朝一夕之功。但调优对于每一项的要求又不仅仅是“知道”或“会使用”这么简单。起码要达到“如何更好的使用”。
常看到性能测试书中说,性能测试不单单是性能测试工程师一个人的事儿。需要DBA 、开发人员、运维人员的配合完成。
但是在不少情况下性能测试是由性能测试人员独立完成的,退一步就算由其它人员的协助,了解系统架构的的各个模块对于自身的提高也有很大帮助,同进也更能得到别人的尊重。
再说性能调优之前,我们有必要再提一下进行测试的目的,或者我们进行性能测试的初衷是什么?
能力验证:验证某系统在一定条件具有什么样的能力。 能力规划:如何使系统达到我们要求的性能能力。 应用程序诊断:比如内存泄漏,通过功能测试很难发现,但通过性能测试却很容易发现。 性能调优:满足用户需求,进一步进行系统分析找出瓶颈,优化瓶颈,提高系统整体性能。
1、一般系统的瓶颈
性能测试调优需要先发现瓶颈,那么系统一般会存在哪些瓶颈:
硬件上的性能瓶颈:
一般指的是CPU、内存、磁盘I/O 方面的问题,分为服务器硬件瓶颈、网络瓶颈(对局域网可以不考虑)、服务器操作系统瓶颈(参数配置)、中间件瓶颈(参数配置、数据库、web服务器等)、应用瓶颈(SQL 语句、数据库设计、业务逻辑、算法等)。
应用软件上的性能瓶颈:
一般指的是应用服务器、web 服务器等应用软件,还包括数据库系统。
例如:中间件weblogic 平台上配置的JDBC连接池的参数设置不合理,造成的瓶颈。
应用程序上的性能瓶颈: 一般指的是开发人员新开发出来的应用程序。
例如,程序架构规划不合理,程序本身设计有问题(串行处理、请求的处理线程不够),造成系统在大量用户方位时性能低下而造成的瓶颈。
操作系统上的性能瓶颈:
一般指的是windows、UNIX、Linux等操作系统。
例如,在进行性能测试,出现物理内存不足时,虚拟内存设置也不合理,虚拟内存的交换效率就会大大降低,从而导致行为的响应时间大大增加,这时认为操作系统上出现性能瓶颈。
网络设备上的性能瓶颈:
一般指的是防火墙、动态负载均衡器、交换机等设备。
例如,在动态负载均衡器上设置了动态分发负载的机制,当发现某个应用服务器上的硬件资源已经到达极限时,动态负载均衡器将后续的交易请求发送到其他负载较轻的应用服务器上。
在测试时发现,动态负载均衡器没有起到相应的作用,这时可以认为网络瓶颈。
性能测试出现的原因及其定位十分复杂,这里只是简单介绍常见的几种瓶颈类型和特征,而性能测试所需要做的就是根据各种情况因素综合考虑,然后协助开发人员\DBA\运维人员一起定位性能瓶颈。
2、一般性能调优步骤
一般性能问题调优的步骤:
步骤一:确定问题
应用程序代码:在通常情况下,很多程序的性能问题都是写出来的,因此对于发现瓶颈的模块,应该首先检查一下代码。
数据库配置:经常引起整个系统运行缓慢,一些诸如oracle 的大型数据库都是需要DBA进行正确的参数调整才能投产的。
操作系统配置:不合理就可能引起系统瓶颈。
硬件设置:硬盘速度、内存大小等都是容易引起瓶颈的原因,因此这些都是分析的重点。
网络:网络负载过重导致网络冲突和网络延迟。
步骤二:确定问题
当确定了问题之后,我们要明确这个问题影响的是响应时间吞吐量,还是其他问题?是多数用户还是少数用户遇到了问题?如果是少数用户,这几个用户与其它用户的操作有什么不用?
系统资源监控的结果是否正常?CPU的使用是否到达极限?I/O 情况如何?问题是否集中在某一类模块中?
是客户端还是服务器出现问题? 系统硬件配置是否够用?实际负载是否超过了系统的负载能力? 是否未对系统进行优化?
通过这些分析及一些与系统相关的问题,可以对系统瓶颈有更深入的了解,进而分析出真正的原因。
步骤三: 确定调整目标和解决方案
得高系统吞吐理,缩短响应时间,更好地支持并发。
步骤四:测试解决方案
对通过解决方案调优后的系统进行基准测试。(基准测试是指通过设计科学的测试方法、测试工具和测试系统,实现对一类测试对象的某项性能指标进行定量的和可对比的测试)
步骤五:分析调优结果
系统调优是否达到或者超出了预定目标?系统是整体性能得到了改善,还是以系统某部分性能来解决其他问题。调优是否可以结束了。
最后,如果达到了预期目标,调优工作就基本可以结束了。
下面算是一个技巧,如面试官问到一个性能问题假设,我不知道性能问题出在哪儿时,可以按照这个思路回答
查找瓶颈时按以下顺序,由易到难:
服务器硬件瓶颈---〉网络瓶颈(对局域网,可以不考虑)---〉服务器操作系统瓶颈(参数配置)---〉中间件瓶颈(参数配置,数据库,web服务器等)---〉应用瓶颈(SQL语句、数据库设计、业务逻辑、算法等)
注:以上过程并不是每个分析中都需要的,要根据测试目的和要求来确定分析的深度。对一些要求低的,我们分析到应用系统在将来大的负载压力(并发用户数、数据量)下,系统的硬件瓶颈在哪儿就够了。
分段排除法 很有效:
性能测试调优应该注意的要点: 要点1: 在应用系统的设计开发过程中,应始终把性能放在考虑的范围内。
要点2: 确定清晰明确的性能目标是关键。
要点3: 必须保证调优后的程序运行正确。
要点4: 系统的性能更大程度上取决于良好的设计,调优技巧只是一个辅助手段。
要点5: 调优过程是迭代渐进的过程,每一次调优的结果都要反馈到后续的代码开发中去。
要点6: 性能调优不能以牺牲代码的可读性和可维护性为代码。
最后感谢每一个认真阅读我文章的人,看着粉丝一路的上涨和关注,礼尚往来总是要有的,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走! 希望能帮助到你!【100%无套路免费领取】
相关文章:

性能测试-性能分析与调优原理总结
性能分析与调优如何下手,先从硬件开始,还是先从代码或数据库。 从操作系统(CPU调度,内存管理,进程调度,磁盘I/O)、网络、协议(HTTP, TCP/IP ),还是…...

【机器学习】4 ——熵
机器学习4 ——熵 文章目录 机器学习4 ——熵前言 前言 熵衡量随机变量不确定性,由克劳德香农(Claude Shannon)在1948年提出,称为香农熵。反映了一个系统中信息的混乱程度或信息量。 其定义为: H ( P ) − ∑ x P …...

linux命令用于删除文本文件中的重复行的命令uniq详解
目录 一、概述 二、基本用法 1、uniq 命令的基本语法 2、常用选项 3、获取帮助 三、主要功能 1. 识别并删除相邻重复行 2. 保留重复行的第一个实例 3. 统计重复次数 4. 忽略指定列的比较 四、示例 1. 删除相邻重复行 2. 显示每一行及其重复次数 3. 只显示重复行 4. …...

PHP智驭未来悦享生活智慧小区物业管理小程序系统源码
智驭未来,悦享生活 —— 探索智慧小区物业管理小程序 一、引言:智慧生活的新篇章 在这个日新月异的时代,科技正以前所未有的速度改变着我们的生活。从智能家居到智慧城市,每一处都闪耀着智慧的光芒。而今天,我要带大家…...

深度学习:怎么看pth文件的参数
.pth 文件是 PyTorch 模型的权重文件,它通常包含了训练好的模型的参数。要查看或使用这个文件,你可以按照以下步骤操作: 1. 确保你有模型的定义 你需要有创建这个 .pth 文件时所用的模型的代码。这意味着你需要有模型的类定义和架构。 2. …...

MMLU-Pro 基准测试数据集上线,含 12k 个跨学科复杂问题,难度提升,更具挑战性!DeepSeek 数学模型一键部署
在大语言模型 (LLM) 蓬勃发展的时代,诸如大规模多任务语言理解 (MMLU) 之类的基准测试,在推动 AI 于不同领域的语言理解与推理能力迈向极限方面,发挥着至关重要的关键作用。 然而,伴随模型的持续改进与优化,LLM 在这些…...

Vue | Vue深入浅出——Vue中的render函数详解
1.render函数 在编写vue单文件的大多数情况下,我们都是使用template模板来创建HTML。然而在一些条件判断比较复杂的场景下,使用JavaScript去描绘HTML的生成逻辑会显得更加的简洁直观。 使用Vue官网的例子来简单说明: 如果自己在开发的时候…...

数学基础 -- 线性代数之奇异值
奇异值与其应用 1. 奇异值定义 对于任意的矩阵 A A A(可以是方阵或非方阵),存在三个矩阵 U U U、 Σ \Sigma Σ 和 V V V,使得: A U Σ V T A U \Sigma V^T AUΣVT 其中: U U U 是一个 m m m \ti…...
Python爬虫使用实例-wallpaper
1/ 排雷避坑 🥝 中文乱码问题 print(requests.get(urlurl,headersheaders).text)出现中文乱码 原因分析: <meta charset"gbk" />解决方法: 法一: response requests.get(urlurl,headersheaders) response.en…...

探索Go语言中的随机数生成、矩阵运算与数独验证
1. Go中的随机数生成 在许多编程任务中,随机数的生成是不可或缺的。Go语言通过 math/rand 包提供了伪随机数生成方式。伪随机数由种子(seed)决定,如果种子相同,生成的数列也会相同。为了确保每次程序运行时产生不同的随机数,我们…...

无线安全(WiFi)
免责声明:本文仅做分享!!! 目录 WEP简介 WPA简介 安全类型 密钥交换 PMK PTK 4次握手 WPA攻击原理 网卡选购 攻击姿态 1-暴力破解 脚本工具 字典 2-Airgeddon 破解 3-KRACK漏洞 4-Rough AP 攻击 5-wifi钓鱼 6-wifite 其他 WEP简介 WEP是WiredEquivalentPri…...
)
牛客练习赛128:Cidoai的平均数对(背包dp)
题目描述 给定 nnn 对数 (ai,bi)(a_i,b_i)(ai,bi) 和参数 kkk,你需要选出一些对使得在满足 bib_ibi 的平均值不超过 kkk 的同时,aia_iai 的和最大,求出这个最大值。 输入描述: 第一行两个整数分别表示 n,kn,kn,k。 接下来 nnn 行&…...

Python世界:简易地址簿增删查改算法实践
Python世界:简易地址簿增删查改算法实践 任务背景编码思路代码实现本文小结 任务背景 该任务来自简明Python教程中迈出下一步一章的问题: 编写一款你自己的命令行地址簿程序, 你可以用它浏览、 添加、 编辑、 删除或搜索你的联系人ÿ…...
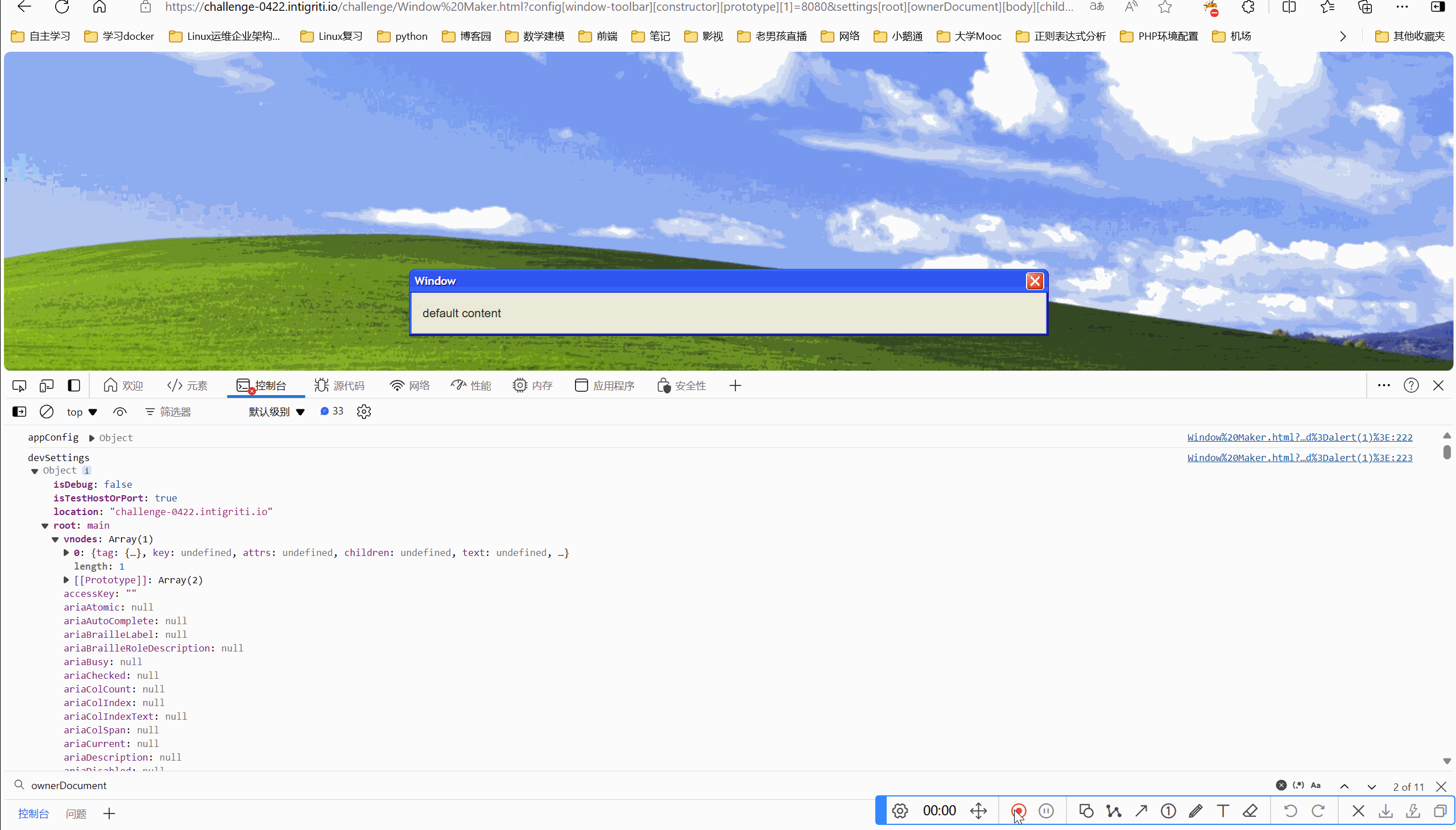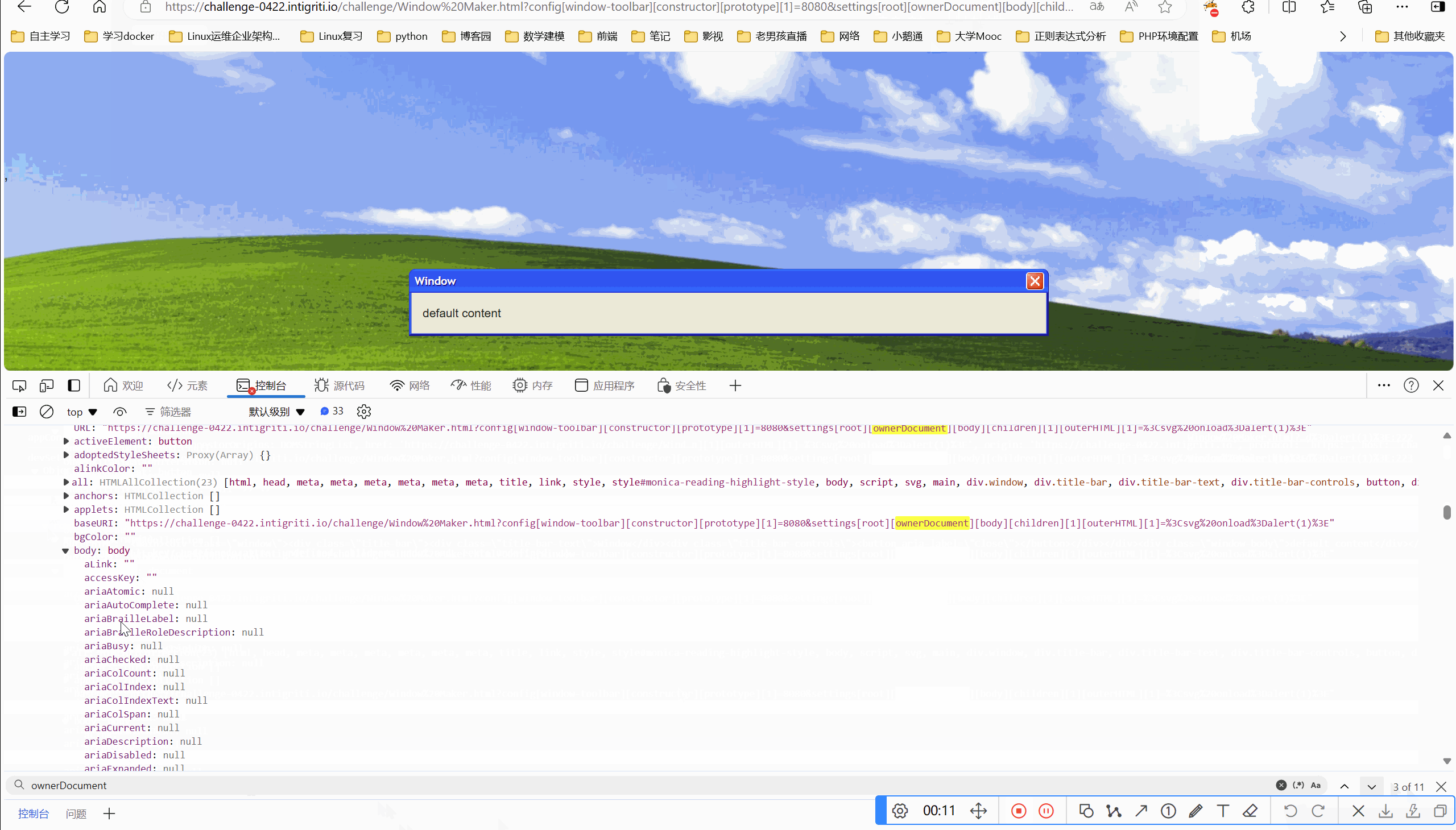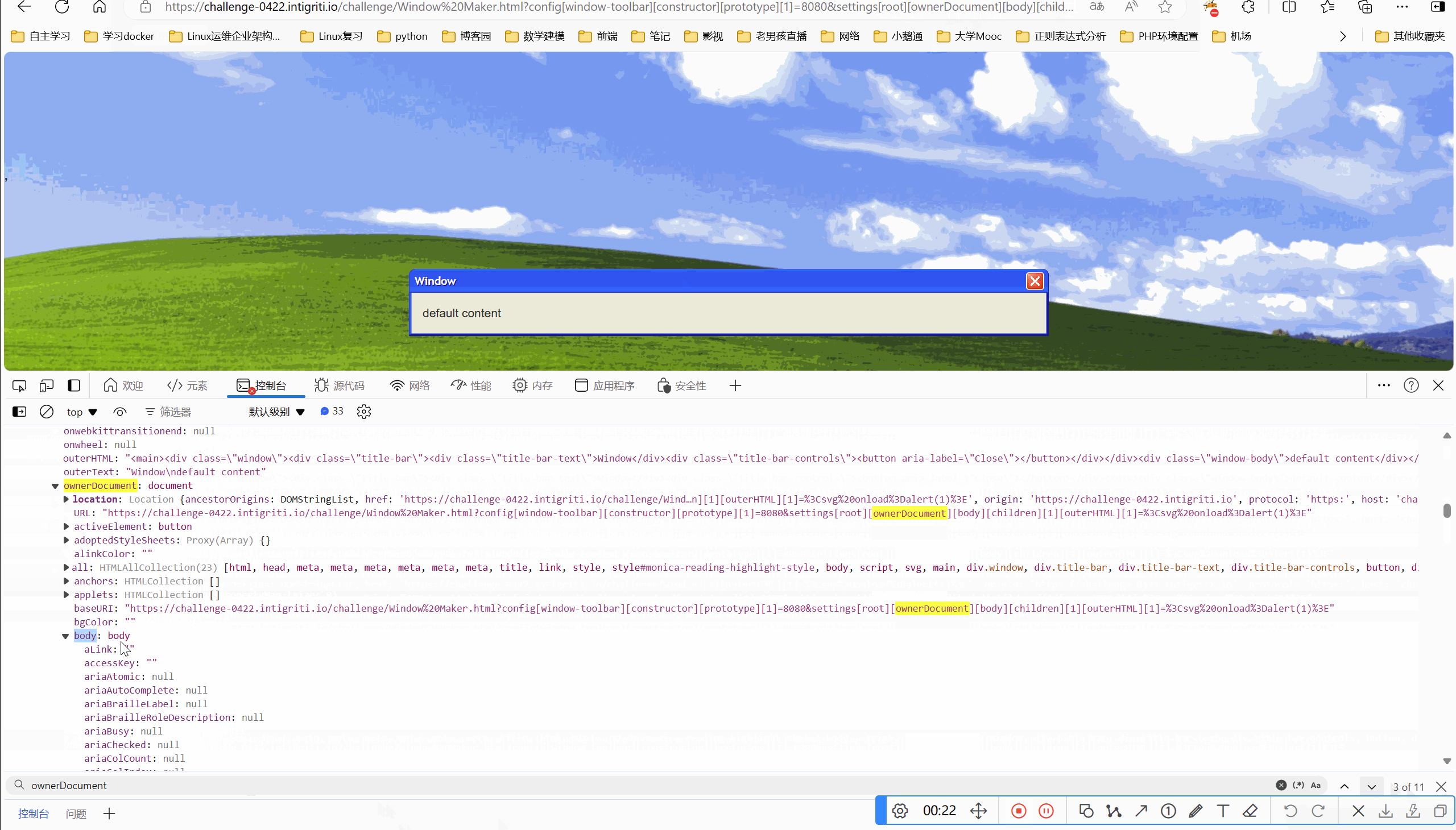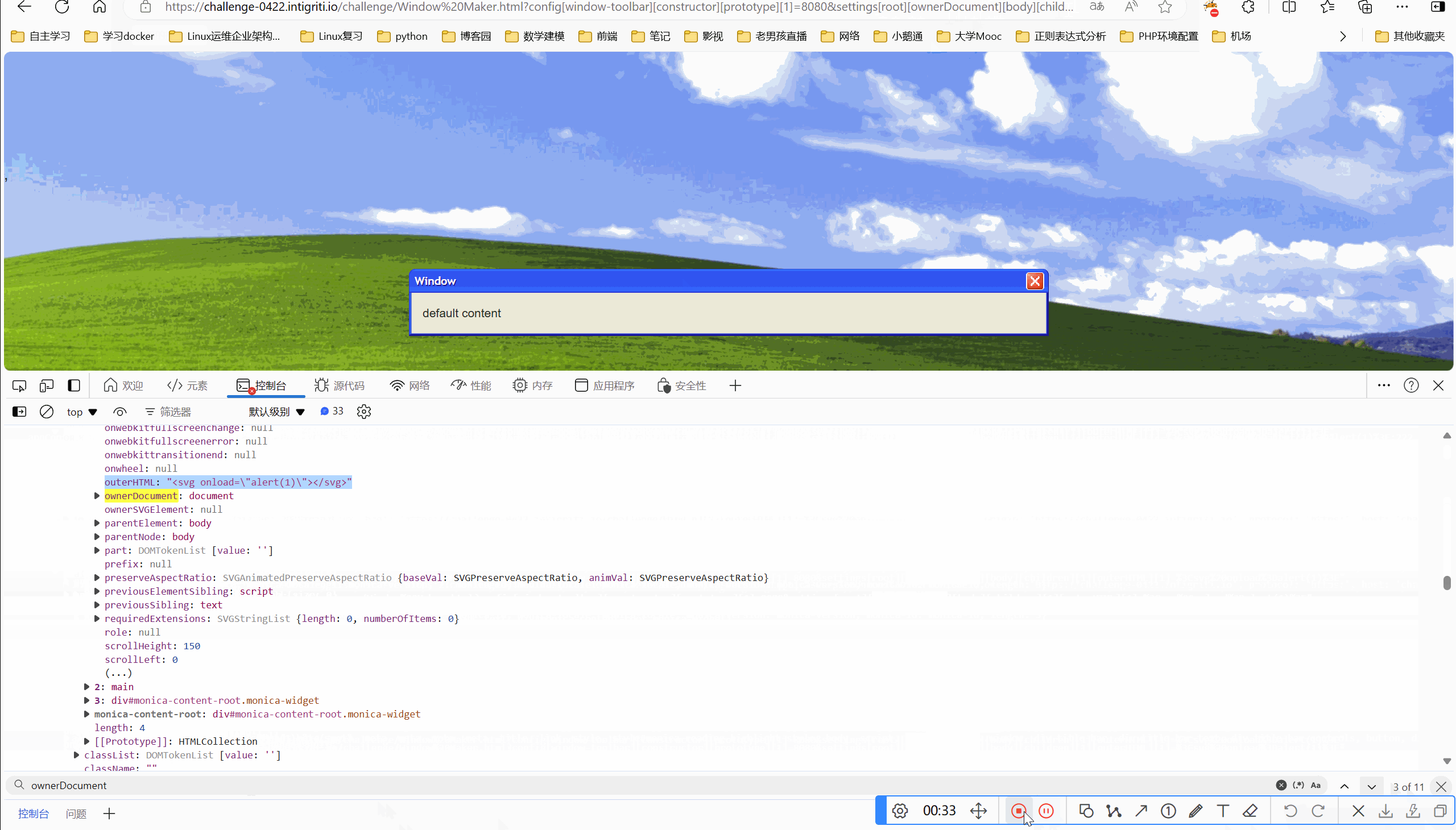
网络安全-intigriti-0422-XSS-Challenge Write-up
目录 一、环境 二、解题 2.1看源码 一、环境 Intigriti April Challenge 二、解题 要求:弹出域名就算成功 2.1看源码 我们看到marge方法,肯定是原型链污染题目 接的是传参,我们可控的点在于qs.config和qs.settings,这两个可…...

Debian Linux 11 使用crash
文章目录 前言一、环境安装1.1 安装debug package1.2 安装crash 二、使用crash 前言 # cat /etc/os-release PRETTY_NAME"Debian GNU/Linux 11 (bullseye)" NAME"Debian GNU/Linux" VERSION_ID"11" VERSION"11 (bullseye)" VERSION_C…...

python列表 — 按顺序找出b表中比a表多出的元素
目录 一、功能描述 二、适用场景 三、代码实现 一、功能描述 有a、b两个列表,a列表有3个元素;b列表有7个元素。b列表多出的一个元素可能在随机的位置,在不影响其他元素的情况下,找到b列表多出的那四个元素,并按照在…...

如何使用Python创建目录或文件路径列表
在 Python 中,创建目录或生成文件路径列表通常涉及使用 os、os.path 或 pathlib 模块。下面是一些常见的任务和方法,用于在 Python 中创建目录或获取文件路径列表。 问题背景 在初始阶段的 Python 学习过程中,可能遇到这样的问题:…...

领夹麦克风哪个品牌好,哪种领夹麦性价比高,无线麦克风推荐
在音频录制需求日益多样化的今天,无线领夹麦克风作为提升音质的关键设备,其重要性不言而喻。市场上鱼龙混杂,假冒伪劣、以次充好的现象屡见不鲜。这些产品往往以低价吸引消费者,却在音质、稳定性、耐用性等方面大打折扣࿰…...
)
苍穹外卖学习笔记(五)
文章目录 二.新增菜品1.图片上传2.具体新增菜品 二.新增菜品 1.图片上传 这里采用了阿里云oss对象存储服务 application.yml alioss:endpoint: ${sky.alioss.endpoint}access-key-id: ${sky.alioss.access-key-id}access-key-secret: ${sky.alioss.access-key-secret}bucket…...

什么是卷积层、池化层、BN层,有什么作用?
什么是卷积层、池化层、BN层,有什么作用? 卷积层池化层BN层 卷积层 定义: 卷积层是CNN中的核心组件,它通过卷积运算对输入数据进行特征提取。卷积层由多个卷积单元组成,每个卷积单元的参数通过反向传播算法优化得到。…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
