461. 汉明距离
一:题目:
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
示例 1:
输入:x = 1, y = 4 输出:2 解释: 1 (0 0 0 1) 4 (0 1 0 0)↑ ↑ 上面的箭头指出了对应二进制位不同的位置。
示例 2:
输入:x = 3, y = 1 输出:1
提示:
0 <= x, y <= 231 - 1
二:代码:
class Solution {
public:int hammingDistance(int x, int y) {int count=0;int t=x^y;for(int i=0;i<32;i++){if(t & 1){count++;}t=t>>1;}return count;}
};三:结果:

相关文章:

461. 汉明距离
一:题目: 两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。 给你两个整数 x 和 y,计算并返回它们之间的汉明距离。 示例 1: 输入:x 1, y 4 输出:2 解释: 1 (0 0…...

开发指南061-nexus权限管理
平台后台服务的核心是组件,管理组件的软件有: Apache的Archiva、JFrog的Artifactory、Sonatype的Nexus。 本平台选择nexus。nexus的权限模型是用户-角色-权限体系:通过组合权限定义角色,通过给用户赋角色来赋权限。有关nexus的权…...

Qt 弹出菜单右键菜单 QMenu 设置不同颜色的子项
概述 在Qt中,可以使用样式表(StyleSheet)来自定义 QMenu 的外观,包括其子项(如菜单项QAction)的颜色。但是,这通常可以设置 QMenu 的整体样式,而不能单独设置某个子项的颜色。不过&…...

Git换行符自动转换参数core.autocrlf的用法
core.autocrlf 是 Git 中用于控制换行符自动转换的配置选项。它有以下几个可能的值: 1. true 作用:在 checkin 时将 CRLF 转换为 LF,在 checkout 时将 LF 转换为 CRLF。适用场景:适用于 Windows 用户,希望在本地文件…...

C语言的结构体类型
在我们使用C语言进行编写代码时,常常会使用已经给定的类型来创建变量,比如int型,char型,double型等,而当我们想创建一些较为复杂的东西时,单单用一个类型变量是没办法做到的,比如我们想创建一个…...

illustrator 收集字体插件VBscript
这是早些年从俄罗斯网站上看到的一个收集字体插件,语言是用VBscript写的,能用,但个别字体不能收集完成,现在Adobe也在illustrator中加入了收集字体打包功能,所以这个也很少用啦。 使用方法: 下好插件,或把下面的代码存入到本地侯后缀名改为.vbs,然后把.ai文件往.vbs文…...

【LLM多模态】文生视频评测基准VBench
note VBench的16个维度自动化评估指标代码实践(待完成)16个维度的prompt举例人类偏好标注:计算VBench评估结果与人类偏好之间的相关性、用于DPO微调 文章目录 note一、相关背景二、VBench评测基准概述:论文如何解决这个问题&…...

通过覆写 url_for 将 flask 应用部署到子目录下
0. 缘起 最近用 flask 写了一个 web 应用,需要部署到服务器上。而服务器主域名已经被使用了,只能给主域名加个子目录进行部署,比如主域名 example.org ,我需要在 example.org/flask 下部署。这时 flask 应用里的内部连接们就出现…...

攻防世界---->埃尔隆德32
做题笔记。 下载 查壳。 32ida 打开。 发现就一个判断。 跟进看看。 // 首次a20 int __cdecl sub_8048414(_BYTE *a1, int a2) {int result; // eaxswitch ( a2 ){case 0:if ( *a1 105 )goto LABEL_19;result 0;break;case 1:if ( *a1 101 ) // e…...

redis短信登录模型
基于Session实现登录 ,...
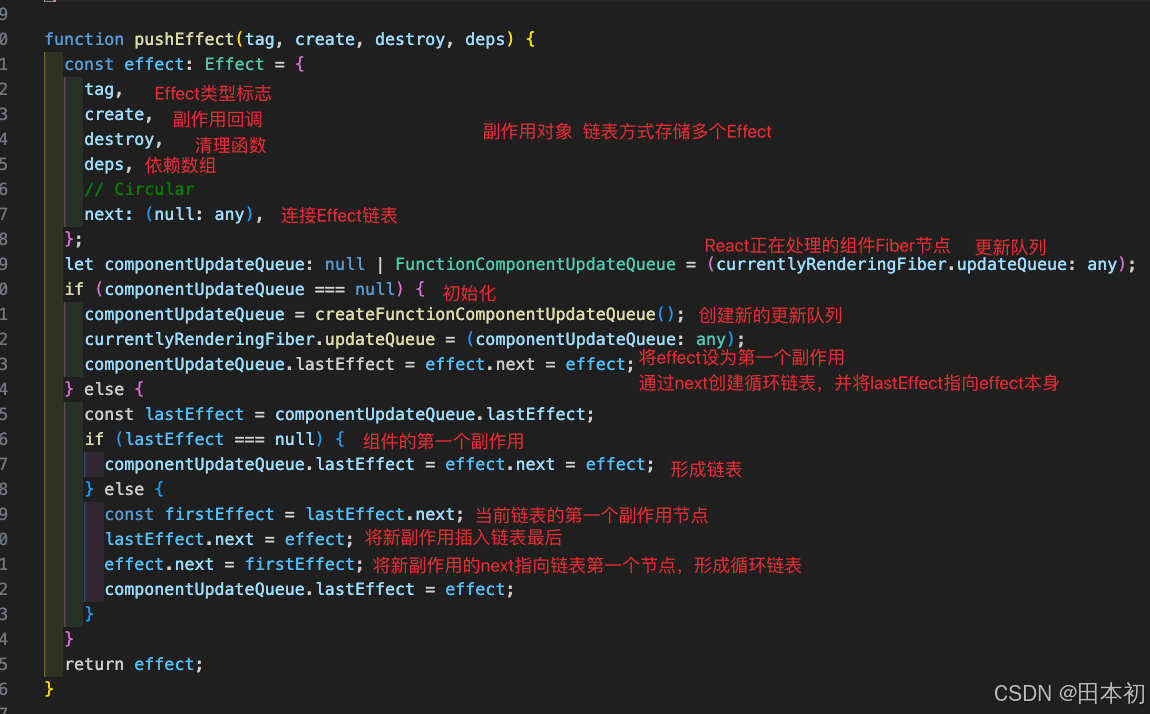
【React】React18.2.0核心源码解读
前言 本文使用 React18.2.0 的源码,如果想回退到某一版本执行git checkout tags/v18.2.0即可。如果打开源码发现js文件报ts类型错误请看本人另一篇文章:VsCode查看React源码全是类型报错如何解决。 阅读源码的过程: 下载源码 观察 package…...

深度学习-目标检测(四)-Faster R-CNN
目录 一.模型框架 二:步骤详细 1.conv layers 2.RPN 3.anchors 4.cls layer分类 5.reg layer回归 6.Proprosal 7.Rol pooling 8.Classification 三.训练 1.训练RPN网络 2.全连接层部分训练: 都看到这里了,点个赞把!&a…...

MATLAB中的无线通信系统设计有哪些最佳实践
在无线通信系统设计领域,MATLAB提供了一套强大的工具箱,使得系统设计、仿真、测试和分析变得更加高效和精确。本文将探讨MATLAB在无线通信系统设计中的最佳实践,包括信号处理、调制与解调、信道建模、误码率分析以及无线通信标准的实现。 1.…...

Java的发展史与前景
🌈个人主页:Yui_ 🌈Linux专栏:Linux 🌈C语言笔记专栏:C语言笔记 🌈数据结构专栏:数据结构 🌈C专栏:C 文章目录 0. Java语言的发展史1.概述1.1 什么是Java1.2 …...

2024年上海小学生古诗文大会倒计时30多天:做几道今年的官方模拟题
2024年上海市小学生古诗文大会自由报名活动的初赛日期于10月19日开始,距离今天只有34天了。 小学生古诗文大会考什么?怎么考呢?今天好真题就带着大家来做一做官方发布的2024年小学生古诗文大会的模拟题,根据往年的经验࿰…...

IDEA 常用配置和开发插件
件市场中搜索并安装“Git Integration”插件。 一、前言 在本篇文章中我会为大家总结一些我自己常用的配置和开发插件,此外也给大家提供一个建议,可以根据自己的项目需求和个人偏好选择适合的插件。另外,IDEA 也在不断更新,可能会…...

还在为企微联系人烦恼?一招解决!企业微信2024年效率升级全攻略
现在信息多得让人眼花,微信里头那些企业微信的联系人是不是让你头疼? 看着满屏的绿色头像,心里想:“我就想和朋友聊聊天,怎么就这么难?”别急,今天教你个办法,轻松搞定这些小烦恼&am…...

【docker npm】npm 私库
1.部署环境 window 11 x64Docker Desktop 4.34.1 (166053) Docker Engine v27.2.0 1.1.Docker 镜像源 1.1.1.Docker Engine 配置 {"builder": {"features": {"buildkit": true},"gc": {"defaultKeepStorage": "32…...

完整gpt应用(自用)
qrc.py 把gpt_qrc.qrc转化成gpt_qrc.py pyrcc5 -o icons_rc.py icons.qrc <RCC><qresource prefix"img"><file>img/53.png</file><file>img/ai.png</file><file>img/关闭.png</file><file>img/最小化.png&l…...

【信息论基础第二讲】离散信源的数学模型及其信息测度包括信源的分类、信源的数学模型、离散信源的信息测度、二元信源的条件熵联合熵
一、信源的分类 二、信源的数学模型 1、信源的概念 在通信系统中,收信者在未收到信息以前,对信源发出什么消息是不确定的、随机的、因此我们可以用随机变量、随机序列或者随机过程来描述信源的输出。严格地说,用概率空间来描述信源输出。 …...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
