Python学习——【2.3】for循环
文章目录
- 【2.3】for循环
- 一、for循环基础语法
- (一)基础语法
- ※、练习
- (二)range语句
- ※、练习
- (三)变量作用域
- 二、for循环嵌套使用
- ※、练习
【2.3】for循环
一、for循环基础语法
(一)基础语法
除了while循环语句外,Python还提供了for循环语句。两者能完成的功能差不多,但仍有所侧重:
1.while循环的循环条件是自定义的,自行控制循环条件;
2.for循环是一种轮询机制,是对一批内容进行逐个处理。
for循环语法如下:
for 临时变量 in 待处理数据集:循环满足条件时执行的代码
从待处理数据集中,逐个取出数据并赋给临时变量。
示例(遍历字符串):
# 定义字符串name
name = "zhangsan"# for循环处理字符串
for x in name:print(x)
输出结果如下:
z
h
a
n
g
s
a
n
注意:
1.与while循环不同,for循环是无法定义循环条件的,只能从被处理的数据集中依次取出内容进行处理。
2.所以,理论上讲,Python的for循环无法构建无限循环(因为被处理的数据集不可能无限大)。
3.for循环内的语句,同样需要注意正确缩进。
※、练习
案例:数一数有几个a
定义字符串变量name,内容为:I eat an apple every day.
通过for循环,遍历此字符串,统计有多少个英文字母a。
我的代码
name = "I eat an apple every day."
count = 0for x in name:if x == 'a':count += 1print(f"{name}中共含有:{count}个字母a")
(二)range语句
对于for循环语法:
for 临时变量 in 待处理数据集:循环满足条件时执行的代码
对于语法中的待处理数据集,严格来说,其被称作:序列类型。
序列类型指,其内容可以一个个依次取出的一种类型,包括:
- 字符串;
- 列表;
- 元组;
- 等等。
for循环语句,本质上是遍历序列类型。
range语句的功能:获得一个数字序列
语法一:
range(num)
获取一个从0开始,到num结束(不含num本身)的数字序列。
如range(5)获得的数据是:[0, 1, 2, 3, 4]。
语法二:
range(num1, num2)
获得一个从num1开始,到num2结束(不含num2本身)的数字序列。
如range(5, 10)获得的数据是:[5, 6, 7, 8, 9]。
语法三:
range(num1, num2, step)
获得一个从num1开始,到num2结束(不含num2本身)的数字序列。
数字之间的步长,以step为准(step默认值为1)。
如range(5, 10, 2)获得的数据是:[5, 7, 9]。
※、练习
案例:有几个偶数
定义一个数字变量num,内容随意。
使用range()语句,获取从1到num的序列,使用for循环遍历它。
在遍历的过程中,统计有多少偶数出现。
我的代码
num = 20
count = 0for i in range(1, num + 1):if i % 2 == 0:count += 1print(f"从1到{num}共有{count}个偶数。")
(三)变量作用域
思考一个问题:
for i in range(5):print(i)print(i)
如上代码,思考一下:最下面那行print(i)语句,能否访问到变量i?
答:规范上不允许;实际上可以。
for循环的变量作用域问题
for 临时变量 in 待处理数据集:循环满足条件时执行的代码
回顾for循环的语法,从数据集中取出的数据赋值给临时变量。顾名思义,它为什么叫“临时变量”呢?
临时变量,在编程规范上,作用范围(作用域),只限定在for循环内部。
而如果在for循环外部访问临时变量:
1.实际上是可以访问到的;
2.在编程规范上,是不允许、不建议这么做的。
如何在for循环外部访问“临时变量”
把临时变量在for循环外部先定义一下即可。这样一来,它本身就是for循环外部的一个普通变量,只不过for循环对它进行了若干次操作而已,后续我再访问它的时候也是正常访问一个普通变量。
i = 0for i in range(5):print(i)print(i)
二、for循环嵌套使用
语法如下:
for 临时变量 in 待处理数据集:循环满足条件应做的事情1循环满足条件应做的事情2循环满足条件应做的事情N...for 临时变量 in 待处理数据集:循环满足条件应做的事情1循环满足条件应做的事情2循环满足条件应做的事情N...
示例:
i = 1for i in range(1, 101):print(f"今天是向小美表白的第{i}天,坚持。")for j in range(1, 11):print(f"送给小美的第{j}朵玫瑰花。")print(f"小美,我喜欢你(第{i}天的表白结束。)")print(f"第{i}天,表白成功。")
另外,while和for也可以相互嵌套。
※、练习
案例:for循环打印九九乘法表
通过for循环,输出如下九九乘法表内容:
1 * 1 = 1
1 * 2 = 2 2 * 2 = 4
1 * 3 = 3 2 * 3 = 6 3 * 3 = 9
1 * 4 = 4 2 * 4 = 8 3 * 4 = 12 4 * 4 = 16
1 * 5 = 5 2 * 5 = 10 3 * 5 = 15 4 * 5 = 20 5 * 5 = 25
1 * 6 = 6 2 * 6 = 12 3 * 6 = 18 4 * 6 = 24 5 * 6 = 30 6 * 6 = 36
1 * 7 = 7 2 * 7 = 14 3 * 7 = 21 4 * 7 = 28 5 * 7 = 35 6 * 7 = 42 7 * 7 = 49
1 * 8 = 8 2 * 8 = 16 3 * 8 = 24 4 * 8 = 32 5 * 8 = 40 6 * 8 = 48 7 * 8 = 56 8 * 8 = 64
1 * 9 = 9 2 * 9 = 18 3 * 9 = 27 4 * 9 = 36 5 * 9 = 45 6 * 9 = 54 7 * 9 = 63 8 * 9 = 72 9 * 9 = 81
我的代码
for i in range(1, 10):for j in range(1, i + 1):print(f"{j} * {i} = {i * j}\t", end='')print()
相关文章:

Python学习——【2.3】for循环
文章目录 【2.3】for循环一、for循环基础语法(一)基础语法※、练习 (二)range语句※、练习 (三)变量作用域 二、for循环嵌套使用※、练习 【2.3】for循环 一、for循环基础语法 (一)…...

Element UI:初步探索 Vue.js 的高效 UI 框架
Element UI:初步探索 Vue.js 的高效 UI 框架 一 . ElementUI 基本使用1.1 Element 介绍1.2 Element 快速入门1.3 基础布局1.4 容器布局1.5 表单组件1.6 表格组件1.6.1 基础表格1.6.2 带斑马纹表格1.6.3 带边框表格1.6.4 带状态的表格 1.7 导航栏组件讲解 二 . 学生列…...

React Native防止重复点击
项目中遇到了点击按钮重复提交的问题,防止重复点击首先是想到的是给点击事件一个定时,下次触发的条件是要距离上一次点击的时间大于N秒的之后才能再执行。 // 防重复点击函数 export const preventRepeatPress {lastPressTi1me: 0, // 上次点击时间…...

如何将Git本地代码推送到Gitee云端仓库
如何将Git本地代码推送到Gitee云端仓库 在使用Git进行版本控制时,将本地代码推送到远程仓库是一个基本且重要的操作。本文将详细介绍如何将你的Git本地代码推送到Gitee(码云)云端仓库。Gitee是一个国内非常流行的代码托管平台,类…...

架构师论文备考-论云原生架构及其应用
摘要 2022年3月,我有幸参与了公司的新智慧公交系统的研发工作。该系统基于B/S架构设计,并以多租户SaaS平台化为发展目标,旨在创建一个功能更全面、性能更卓越、稳定性更强、用户体验更佳的公交调度一体化平台。在这一项目中,我主要…...

12.java面向对象:java构造器
构造器 一个类即使什么都不写,也会存在一个方法。 假如我创建了一个类叫Student里面什么都不写,然后使用StudentDemo创建对象,运行没有结果,也没有报错。 public class Student {}public class StudentDemo {public static voi…...

微服务之间的安全通信
在微服务架构中,服务之间的通信是系统的核心部分。然而,由于服务的分布式和独立性,确保它们之间的通信安全至关重要。如果没有适当的安全机制,微服务系统可能会暴露在各种网络攻击和安全漏洞中。本文将讨论几种常见的微服务间安全…...
全面掌握 Jest:从零开始的测试指南(下篇)
在上一篇测试指南中,我们介绍了Jest 的背景、如何初始化项目、常用的匹配器语法以及钩子函数的使用。这一篇篇将继续深入探讨 Jest 的高级特性,包括 Mock 函数、异步请求的处理、Mock 请求的模拟、类的模拟以及定时器的模拟、snapshot 的使用。通过这些技…...

如何利用UML进行领域建模
如何利用UML进行领域建模 领域建模是通过创建抽象模型来反映业务领域中的核心概念、实体及其之间的关系。UML(统一建模语言)是进行领域建模的常用工具,它能帮助我们可视化地设计系统架构和业务逻辑。在这篇讲解中,我们将详细解释…...

Vue实用操作篇-1-第一个 Vue 程序
安装 Vue 非常的简便,只需下载好 Vue 对应的 .js 文件,在 html 中引入 vue.js 即可使用 Vue 下载好了 vue.js 我们便可以编写我们的第一个 vue 程序了 <!doctype html> <html lang"zh-CN"><head><meta charset"utf…...

Qwen2-VL的微调及量化
一、Qwen2-VL简介 Qwen2-VL是Qwen-VL的升级版本,能力更强,性能全面提升。尤其是72B参数的版本更是取了惊人的成绩。它可以读懂不同分辨率和不同长宽比的图片,在 MathVista、DocVQA、RealWorldQA、MTVQA 等基准测试创下全球领先的表现…...

[数据集][目标检测]车窗状态检测车窗开关检测数据集VOC+YOLO格式299张3类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):299 标注数量(xml文件个数):299 标注数量(txt文件个数):299 标注类别…...

自动泊车系统中的YOLOv8 pose关键点车位线检测
自动泊车系统中的YOLOv8关键点车位线检测技术解析 引言 随着智能驾驶技术的快速发展,自动泊车功能成为了现代汽车的重要组成部分。它不仅能够提高驾驶的安全性,还能在一定程度上解决城市停车难的问题。在自动泊车系统中,准确识别停车位的位置…...

Java html生成pdf和图片
在 Java 项目中将 HTML 生成图片是一项常见需求,特别是用于生成报告、预览页面截图等。不同的库和工具在渲染能力、性能以及支持的功能上有所不同。以下是几种主流的技术选型和对比,帮助你选择适合的解决方案。 技术对比总结 技术名称优点缺点适用场景…...

JavaWeb笔记整理——Redis
目录 Redis数据类型 各种数据类型的特点 Redis常用命令 字符串操作命令 哈希操作命令 列表操作命令 集合操作命令 有序集合操作命令 通用命令 在Java中操作Redis Spring Data Redis的使用方式 操作字符串类型的数据 编辑操作hash类型的数据 编辑 操作列表类…...
常用命令)
数据库(mysql)常用命令
一.常见的数据库端口号 Mysql默认端口:3306 oracle 默认端口:1521 Sql server 默认端口:1433 注:Mysql采用 的是C/S(客户端/服务器端)架构 二.sql 语法基础 服务器,数据库,数据表,记录,字段之间的关系: 一台Mysql服务器可以管理多个数据库 一个数据库可以存在多张二维表…...
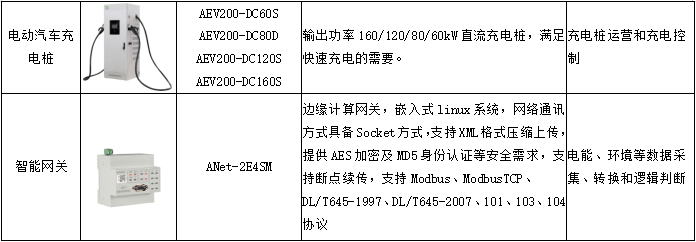
源网荷储一体化新型电力系统解决方案
风光装机快速增长,加剧电力系统不可控性。截至2023H1,我国风电装机389.21GW,太阳能装机470.67GW,风光合计占总装机的31.76%。其中,2023年H1我国风电新增装机22.99GW,对比22年同期新增12.94GW,同…...

树莓派安装 OpenCV 教程
以下是在树莓派上安装 OpenCV 的教程: 笔者当前Python版本:3.7.3 一、更新树莓派系统 在终端中运行以下命令: sudo apt update sudo apt upgrade二、安装必要的依赖项 安装构建工具和图像 I/O 库: sudo apt install build-e…...

01,大数据总结,zookeeper
1 ,zookeeper :概述 1.1,zookeeper:作用 1 ,大数据领域 :存储配置数据 例如:hadoop 的 ha 配置信息,hbase 的配置信息,都存储在 zookeeper 2 ,应用领…...

伪工厂模式制造敌人
实现效果 1.敌人方实现 敌人代码 using UnityEngine; using UnityEngine.UI;public class EnemyBasics : MonoBehaviour {public int EnemySpeed { get; internal set; }public int EnemyAttackDistance { get; internal set; }public int EnemyChaseDistance { get; interna…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果