分治法实现合并排序(归并排序),理解分治算法思想,实现分治算法的完美例子合并排序(含码源与解析)

🎊【数据结构与算法】专题正在持续更新中,各种数据结构的创建原理与运用✨,经典算法的解析✨都在这儿,欢迎大家前往订阅本专题,获取更多详细信息哦🎏🎏🎏
🪔本系列专栏 - 数据结构与算法_勾栏听曲_0
🍻欢迎大家 🏹 点赞👍 评论📨 收藏⭐️
📌个人主页 - 勾栏听曲_0的博客📝
🔑希望本文能对你有所帮助,如有不足请指正,共同进步吧🏆
🎇一个人无论在祈祷什么,他祈祷的都只不过是一个奇迹。所有祈祷文无非都是一个意思:“伟大的上帝啊,请使二乘二不等于四吧!”📈
分治法
算法思想
时间效率分析
合并排序
分治法
算法思想
分治法可能是最著名的通用算法设计技术了。虽然它的名气可能和它那好记的名字有关,但它的确是当之无愧的:很多非常有效的算法实际上就是这个通用算法的特殊实现。其实,分治法是按照以下方案工作的。
(1)将一个问题划分为同一类型的若干子问题,子问题最好规模相同。
(2)对这些子问题求解(一般使用递归方法,但在问题规模足够小时,有时也会利用另一个算法)。
(3)有必要的话,合并这些子问题的解,以得到原始问题的答案。
分治法的流程可以参见下图,该图描述的是将一个问题划分为两个较小子问题的例子,也是最常见的情况(至少那些设计运行在单CPU机器上的分治算法是这样的)。

时间效率分析
在分治法最典型的运用中,问题规模为n的实例被划分为两个规模为n/2的实例。更一般的情况下,一个规模为n的实例可以划分为b个规模为n/b的实例,其中α个实例需要求解(这里,a和b是常量,a≥1,b>1)。为了简化分析,我们假设n是b的幂,对于算法的运行时间T(n),我们有下列递推式:
T(n) =aT(n / b)+ f(n)
其中,f(n)是一个函数,表示将问题分解为小问题和将结果合并起来所消耗的时间(对于求和的例子来说,a = b = 2,f(n)= 1)。上述递推式被称为通用分治递推式(generaldivide-and-conquer recurrence)。显然,T(n)的增长次数取决于常量a和b的值以及函数f(n)的增长次数。在分析许多分治算法的效率时,可以应用下列定理来大大简化我们的工作。
主定理 如果在递推式(5.1)中 f(n)e e(n*),其中d≥0,那么
其中,当a < 时,该问题的时间复杂度为n的d次方
当a = 时,该问题的时间复杂度为n的d次方乘一个对数级
当a > 时,该问题的时间复杂度为n的log b为底a次方
合并排序
合并排序是成功应用分治技术的一个完美例子。对于一个需要排序的数组A[0..n -1],合并排序把它一分为二:A[0..[n / 2| - 1]和A[ [n / 2 ]..n-1],并对每个子数组递归排序,然后把这两个排好序的子数组合并为一个有序数组。
下图演示的是用合并排序算法对数列8,3,2,9,7,1,5,4进行排序的操作过程。
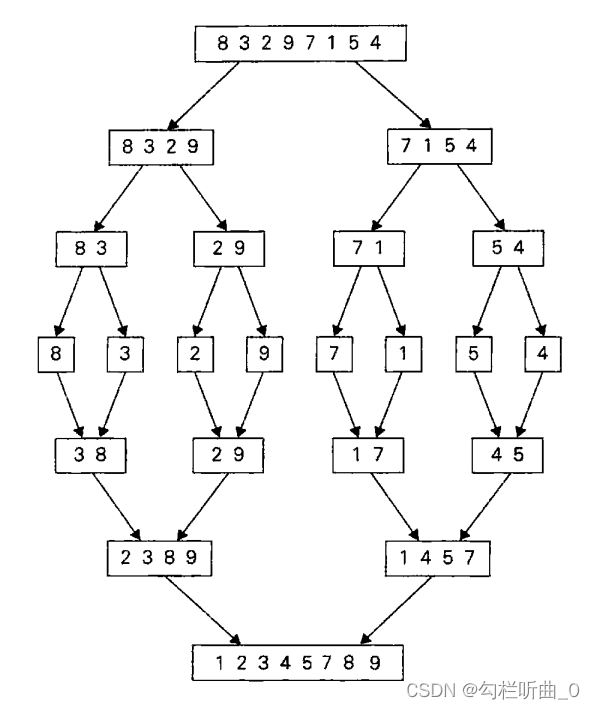
接下来通过视频演示来了解合并排序算法对数列8,3,2,9,7,1,5,4进行排序的操作过程。
合并排序_分治法
代码实现:
#include <stdio.h>void merge(int arr[], int l, int m, int r) {int i, j, k;int n1 = m - l + 1;int n2 = r - m;/* 创建临时数组 */int L[n1], R[n2];/* 复制数据到临时数组 arrays L[] 和 R[] */for (i = 0; i < n1; i++)L[i] = arr[l + i];for (j = 0; j < n2; j++)R[j] = arr[m + 1+ j];/* 归并临时数组到 arr[l..r]*/i = 0; // 初始化第一个子数组的索引j = 0; // 初始化第二个子数组的索引k = l; // 初始归并子数组的索引while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;}else {arr[k] = R[j];j++;}k++;}/* 复制 L[] 的保留元素 */while (i < n1) {arr[k] = L[i];i++;k++;}/* 复制 R[] 的保留元素 */while (j < n2) {arr[k] = R[j];j++;k++;}
}/* l 为左侧索引,r 为右侧索引 */
void mergeSort(int arr[], int l, int r) {if (l < r) {// 求中间位置,防止 (l+r) 的和超过 int 类型最大值int m = l+(r-l)/2;// 递归排序左半部分mergeSort(arr, l, m);// 递归排序右半部分mergeSort(arr, m+1, r);// 合并merge(arr, l, m, r);}
}
相关文章:

分治法实现合并排序(归并排序),理解分治算法思想,实现分治算法的完美例子合并排序(含码源与解析)
🎊【数据结构与算法】专题正在持续更新中,各种数据结构的创建原理与运用✨,经典算法的解析✨都在这儿,欢迎大家前往订阅本专题,获取更多详细信息哦🎏🎏🎏 🪔本系列专栏 -…...
)
Typescript 类 (class)
基本用法 (通过关键字 class) // 基本用法 class VueService {constructor() {} // 构造器 } 类的约束(通过关键字 implements) // 接口定义属性类型 interface VueProps {name: stringinit: () > void }// 约束类 class VueService implements Vue…...
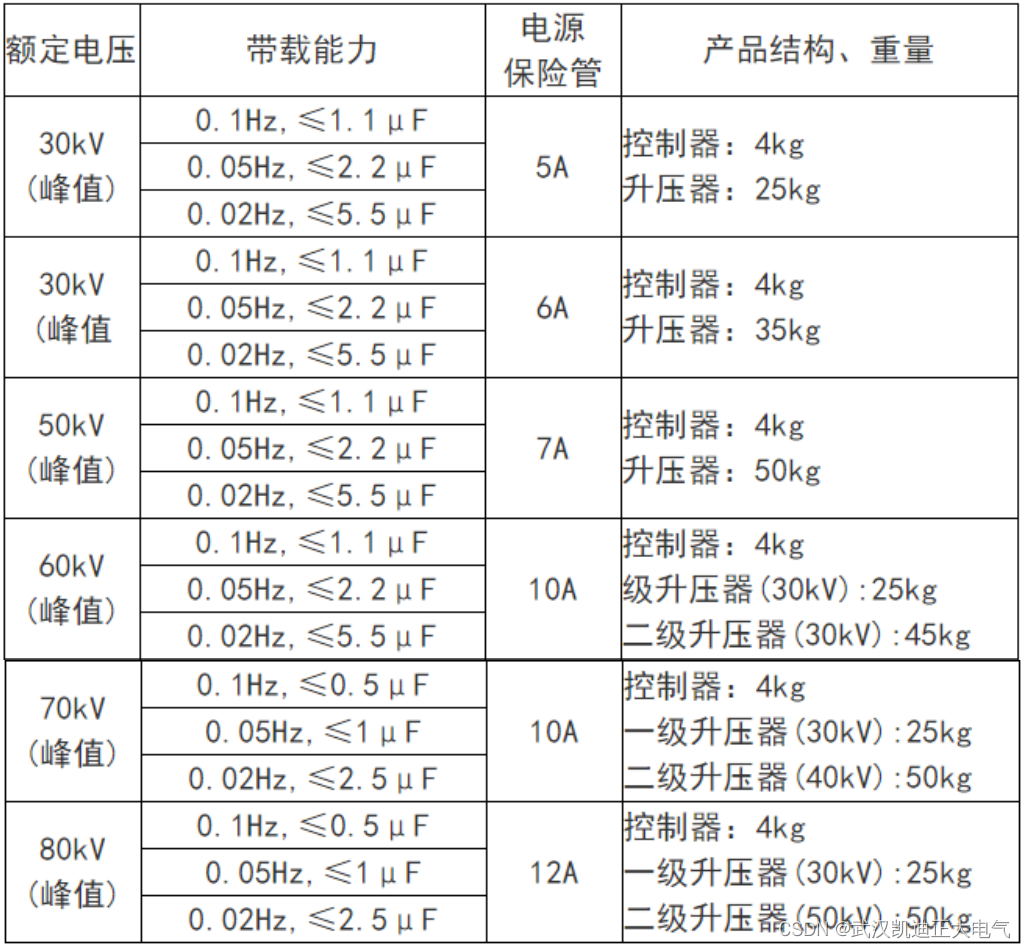
KDZD程控超低频高压发生器
一、产品概述 本产品接合了现代数字变频技术,采用微机控制,升压、降压、测量、保护自动化。由于电子化,所以体积小重量轻、大屏幕液晶显示,清晰直观、且能显示输出波形、打印试验报告。 设计指标符合《电力设备专用测试仪器通用…...
)
【华为OD机试 2023最新 】 过滤组合字符串(C++)
文章目录 题目描述输入描述输出描述用例题目解析C++题目描述 数字0、1、2、3、4、5、6、7、8、9分别关联 a~z 26个英文字母。 0 关联 “a”,”b”,”c”1 关联 “d”,”e”,”f”2 关联 “g”,”h”,”i”3 关联 “j”,”k”,”l”4 关联 “m”,”n”,”o”5 关联 “p”,”q”…...

Java笔记034-坦克大战【2】
目录 坦克大战【2】 线程-应用到坦克大战 坦克大战0.3 思路分析: 代码实现: 坦克大战0.4 增加功能 特别说明 思路分析: 代码实现: 坦克大战0.5 增加功能 思路分析: 代码实现: 坦克大战【2】 …...

【算法】【数组与矩阵模块】桶排序思想解决无序数组排序后相邻数间的最大差值
目录前言问题介绍解决方案代码编写java语言版本c语言版本c语言版本思考感悟写在最后前言 当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~ 在此感谢左大神让我对算法有了新的感悟认识! 问题介绍 …...
C语言—函数
函数库函数自定义函数函数的参数函数的调用函数的嵌套调用和链式访问函数的声明和定义函数递归递归与迭代函数递归的经典题目维基百科(台湾方面维护的,翻译形式跟大陆有所差异)中对函数的定义:子程序在计算机科学中,子…...

Autosar模式管理实战系列03-基于Davinci工具的WDGM配置
本文框架 前言1.WdgMConfigSet 配置2. 新建监控实体(SE)2.1 新建检测点(Checkpoint)2.2 设置 WdgMInternalTransitions3. WdgMLocalStatusParams配置4. WdgMAliveSupervision配置5. 代码插入指导前言 前面我们介绍了WdgM(看门狗管理)是一个 AutoSAR 的基础模块,负责管理看门…...

AutoML-sklearn and torch
一、auto-sklearn 1.1 环境依赖 额外安装swig 第三方库 linux 支持, mac,windows不支持 1.2 示例代码 time_left_for_this_task 设定任务最大时间 per_run_time_limit 每个子任务最大训练时间 include 可以限制任务训练的模型 import autosklearn.classific…...

《扬帆优配》算力概念股大爆发,主力资金大扫货
3月22日,9股封单金额超亿元,工业富联、鸿博股份、鹏鼎控股分别为3.01亿元、2.78亿元、2.37亿元。 今日三大指数团体收涨,收盘共34股涨停,首要集中于数字经济方向,其间云核算、CPO大迸发。除去5只ST股,算计2…...

机械臂+底盘三维模型从solidworks到moveit配置功能包
文章目录 导出底盘STEP加载机械臂模型组合机械臂和底盘三维模型导出URDF在moveit中进行配置新建工作目录设置ROS工作空间的环境变量进入moveit setup加载URDF文件self-CollisionsPlanning groupsRobot posesControllersSimulationAuthor information生成配置包在rviz中进行可视…...
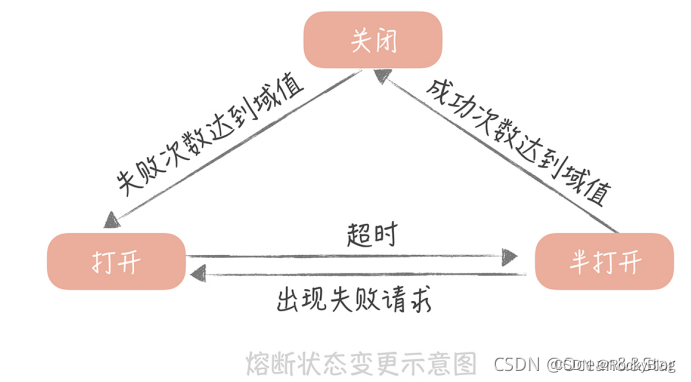
高并发系统设计:缓存、降级、限流、(熔断)
高并发系统设计:缓存、降级、限流、(熔断) 在开发高并发系统时有三把利器用来保护系统:缓存、降级和限流。 非核心服务可以采用降级、熔断,核心服务采用缓存和限流(隔离流量可以最大限度的保障业务无损)。 缓存 缓…...

《辉煌优配》放量大涨,A股成交额重回万亿!PCB板块继续领跑
多只绩优PCB概念股超跌。 今日A股放量反弹,成交额从头站上万亿关口。芯片板块掀涨停潮,景嘉微、芯原股份20cm涨停,紫光国微、兆易创新、跃岭股份等封板;AI算力、存储器、光模块、云核算等板块全线拉升,板块内个股再度批…...
Vue封装的过度与动画
动画效果 先把样式封装好,然后设置一个动画 不需要vue也能实现的动画的效果,我们只需要判断一下,然后动态的添加和删除类名即可 那能不能不自己写动态,就靠vue 首先我们要靠<transition>标签把需要动画的包裹起来 vue中…...
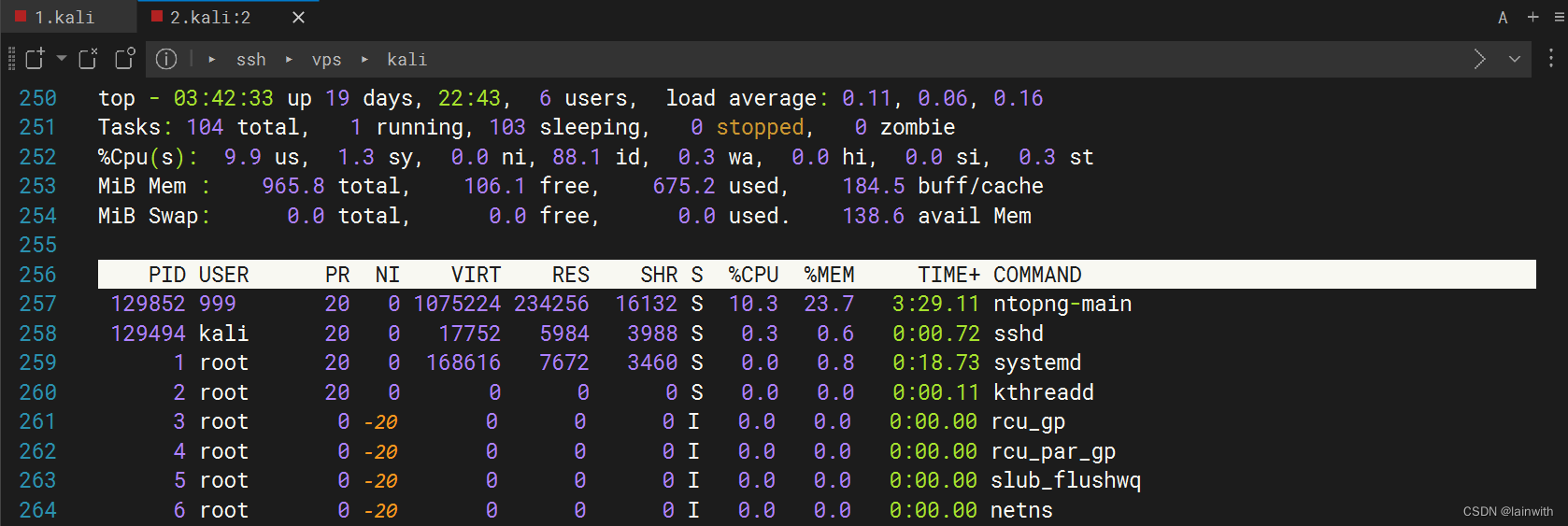
流量监控-ntopng
目录介绍安装使用介绍 ntopng是原始ntop的下一代版本,ntop是监视网络使用情况的网络流量探测器。ntopng基于libpcap,并且以可移植的方式编写,以便实际上可以在每个Unix平台,MacOSX和Windows上运行。 ntopng(是的&…...

C++ 21 set容器
目录 一、set容器 1.1 简介 1.2 构造和赋值 1.3 大小和交换 1.4 插入和删除 1.5 查找和统计 1.6 set和multiset区别 1.7 内置类型指定排序规则 1.8 自定义数据类型指定排序规则 一、set容器 1.1 简介 ① set容器中所有元素在插入时自动被排序。 ② set容器和multise…...
什么是JWT
JSON Web Token(缩写 JWT)是目前最流行的跨域认证解决方案。 传统的session认证 http协议本身是一种无状态的协议,而这就意味着如果用户向我们的应用提供了用户名和密码来进行用户认证,那么下一次请求时,用户还要再一…...
Gradle7.4安装
前置:本文基于IntelliJ IDEA 2022.2.1 、jdk1.8进行安装 目录 1.挑选Gradle版本 2.系统变量设置 1.挑选Gradle版本 gradle兼容性差, 1.跟idea会有版本问题。 2.跟springboot也有兼容问题Spring Boot Gradle Plugin Reference Guide 首先查询版本&…...
【华为OD机试 2023最新 】 箱子之字形摆放(C++ 100%)
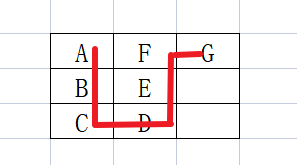
文章目录 题目描述输入描述输出描述备注用例题目解析C++题目描述 有一批箱子(形式为字符串,设为str), 要求将这批箱子按从上到下以之字形的顺序摆放在宽度为 n 的空地,请输出箱子的摆放位置。 例如:箱子ABCDEFG,空地宽度为3,摆放结果如图: 则输出结果为: AFG BE CD …...

Matplotlib库入门
Matplotlib库的介绍 什么是Matplotlib库? Matplotlib是一个Python的数据可视化库,用于绘制各种类型的图表,包括线图、散点图、条形图、等高线图、3D图等等。它是一个非常强大和灵活的库,被广泛用于数据科学、机器学习、工程学、…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
