OpenAI o1解决了「Quiet-STaR」的挑战吗?
随着OpenAI o1近期的发布,业界讨论o1关联论文最多之一可能是早前这篇斯坦福大学和Notbad AI Inc的研究人员开发的Quiet-STaR,即让AI学会先安静的“思考”再“说话” ,回想自己一年前对于这一领域的思考和探索,当初也将这篇论文进行了引用,现将部分内容以节选回忆的方式再一次分享给大家:
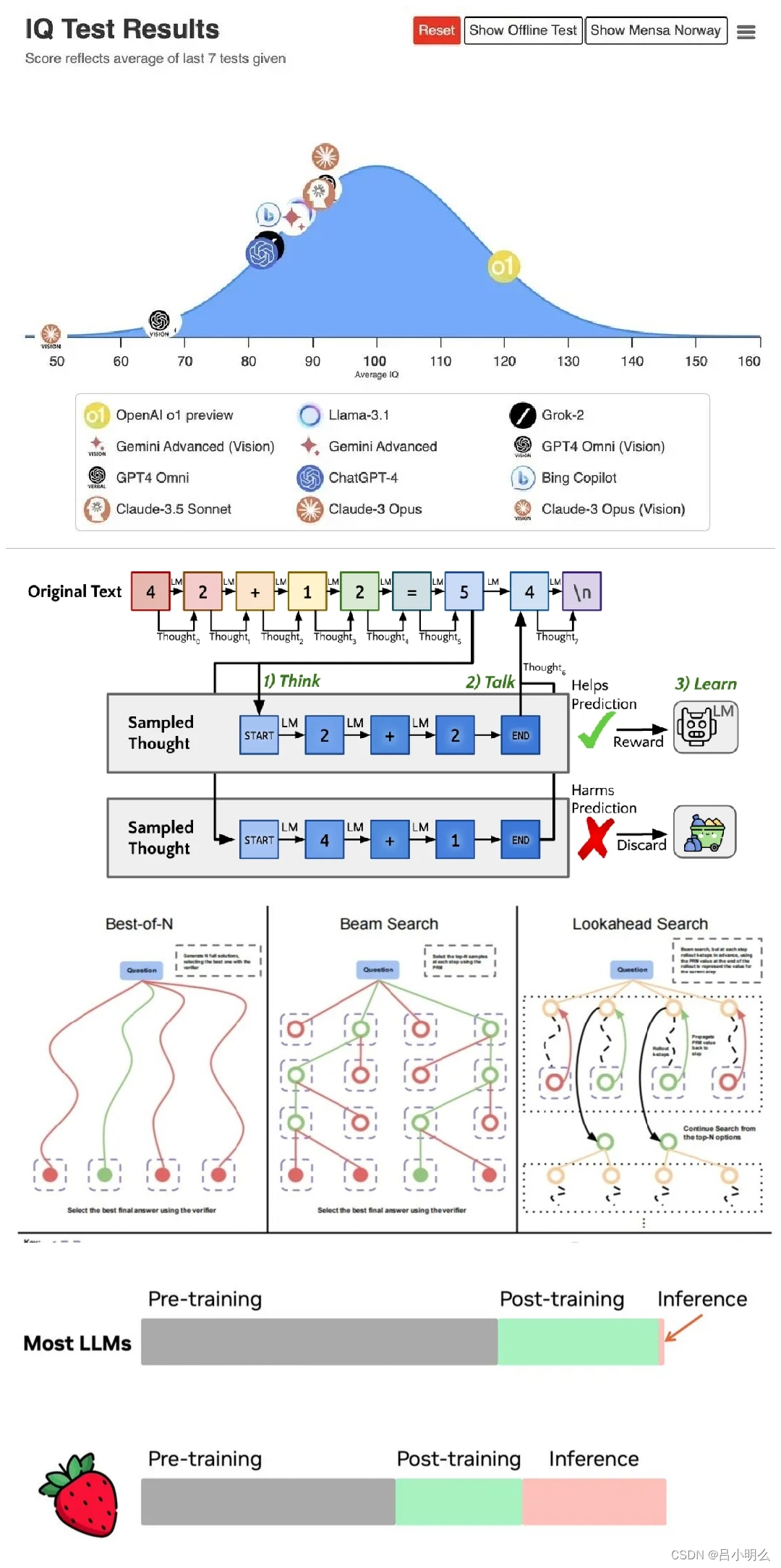
笔记节选自我半年前那篇「融合RL与LLM思想探寻世界模型以迈向AGI」10万字文章,感兴趣完整的小伙伴儿可以访问我的主页置顶或专栏收录
引用原文:↓
值得注意的是,这篇论文所提出的模型名字非常有意思「Quiet-STaR」,似乎预示着什么..论文中的Quiet-STaR 是以一种通用和可扩展的方式学习推理的语言模型。
与上一篇不同,论文中将更多精力聚焦在推理任务数据上而非E2E模型结构或训练方法上。通过在多样化网络文本中隐含的丰富推理任务的范围上进行训练,而不是狭义地专门为特定数据集进行训练,Quiet-STaR 指引了更健壮和适应性更强的语言模型的方向。论文的结果证明了这种方法的潜力,Quiet-STaR 在提高下游推理性能的同时生成了具有质量意义的理由。论文相信这也开启了许多潜在的未来方向 - 例如,可以尝试对思考进行集成,以进一步提高对未来token的预测。
此外,如果语言模型能够预测何时思考是有用的,例如通过在预测之前放置混合头,那么预测的混合权重可以用于在生成过程中动态分配计算资源。
通常,语言模型可以通过对问答数据集进行采样推理来自行训练其推理能力,即尝试回答问题、在推理导致正确最终答案时对其进行训练,然后重复该过程迭代解决更困难的问题。
然而,从策划的问答数据集进行训练限制了推理的规模和普遍性。问答数据集,尤其是高质量的数据集,需要经过深思熟虑的策划,并且天生只能涵盖一部分推理任务。
从而,论文扩展了STaR - 语言模型不是学习在特定任务(如数学问答)上推理,而是训练语言模型生成推理来帮助它从大型互联网文本语料库推断未来文本。
因此,论文允许语言模型从语言中存在的多样化任务中学习。这建立在当前语言建模范式的一个基本直觉之上,即"语言模型是无监督的多任务学习者"。与STaR一样,论文利用语言模型现有的推理能力来生成理由,并使用基于REINFORCE的奖励对语言模型及其生成的理由进行训练。论文将这种技术称为Quiet-STaR,因为它可以被理解为"悄悄地"应用STaR,训练模型在说话之前思考。
相关文章:

OpenAI o1解决了「Quiet-STaR」的挑战吗?
随着OpenAI o1近期的发布,业界讨论o1关联论文最多之一可能是早前这篇斯坦福大学和Notbad AI Inc的研究人员开发的Quiet-STaR,即让AI学会先安静的“思考”再“说话” ,回想自己一年前对于这一领域的思考和探索,当初也将这篇论文进行…...

PDF产品册营销推广利器FLBOOK
在互联网高速发展的时代,营销推广已成为企业拓展市场的重要手段。而一款优秀的营销工具,可以为企业带来事半功倍的推广效果。今天,就为大家介绍一款集创意与实用于一体的PDF产品册营销推广利器——FLBOOK,帮助企业轻松提升品牌影响…...

华为OD机试 - 字符串划分(Python/JS/C/C++ 2024 E卷 100分)
华为OD机试 2024E卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试真题(Python/JS/C/C)》。 刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,…...

nginx和php-fpm连接超时的相关配置以及Nginx中的try_files以及root、alias的使用
一、nginx和php-fpm连接超时的相关配置 线上的PHP服务器架构大都是nginx proxy->nginx web->php-fpm。在服务器运行正常,服务器之间的连接正常,未被防火墙阻止的情况下,对这种架构排查504报错时需要注意以下几个地方的参数。 1是nginx…...

在MAC中Ollama开放其他电脑访问
ollama安装完毕后默认只能在本地访问,之前我都是安装其他的软件之后可以结合开放其他端口访问,其实是可以新增或修改下电脑的系统配置,就可以打开端口允许除本机IP或localhost访问。 步骤如下: 1、查看端口(默认是&…...
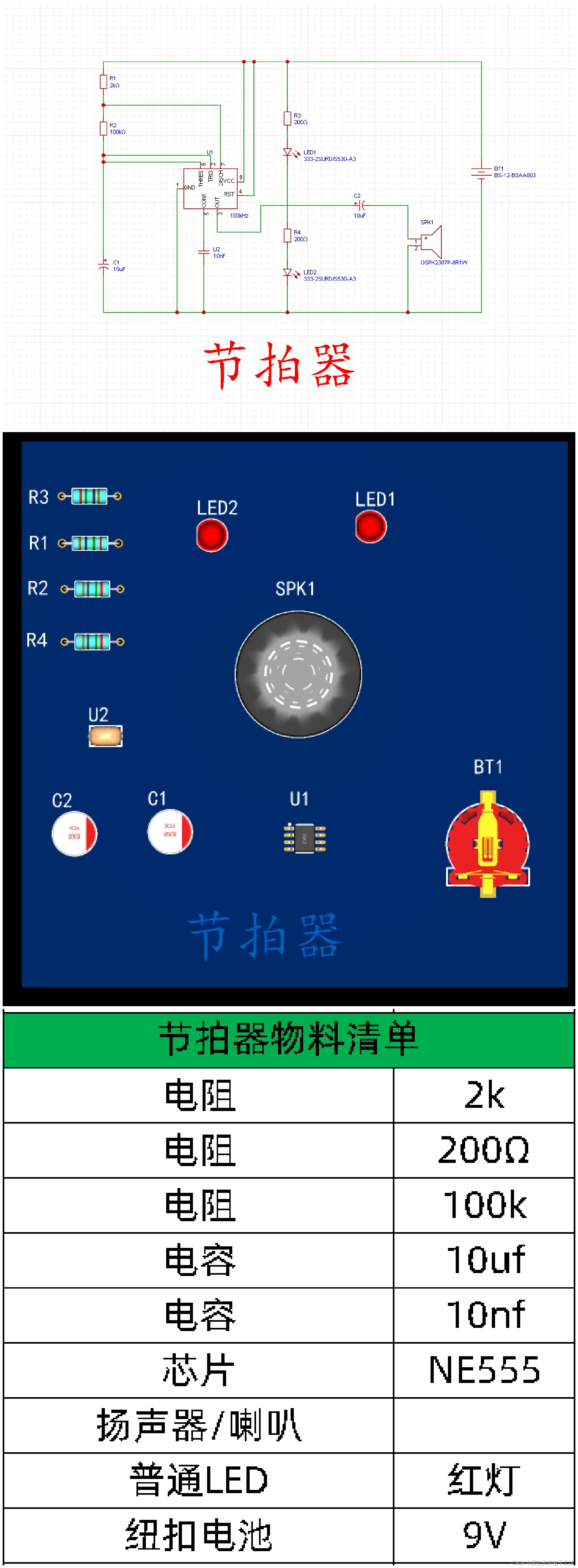
NE555芯片制作的节拍器
NE555芯片的节拍器,以一定的频率发出声音和闪烁灯光,起到节拍指示的作用。...
)
如何使用 Next.js 进行服务端渲染(Server-Side Rendering, SSR)
文章目录 前言步骤 1: 创建 Next.js 应用步骤 2: 创建页面组件示例页面组件 步骤 3: 自定义 _app.js 文件步骤 4: 自定义 _document.js 文件步骤 5: 运行应用步骤 6: 构建和部署总结 前言 Next.js 本身就支持 SSR 并提供了一系列内置的方法来简化这个过程。下面将详细介绍如何使…...

【machine learning-八-可视化loss funciton】
可视化lossfunction loss funciton可视化损失函数等高图 loss funciton 上一节讲过损失函数,也就是代价函数,它是衡量模型训练好坏的指标,对于线性回归来说,模型、参数、损失函数以及目标如下:、 损失函数的目标当然…...

Android 将EasyPermissions进一步封装,使得动态权限申请更加简明
1.引入依赖: implementation pub.devrel:easypermissions:3.0.0 2.在BaseActivity处理统一的结果回调和请求Code 核心内容: (1)处理Activity本身继承的方法onRequestPermissionsResult (2)实现接口EasyPermissions.PermissionCallbacks来接收请求结果 (3)定义申请权…...

我的AI工具箱Tauri版-VideoReapeat视频解说复述克隆
本教程基于自研的AI工具箱Tauri版进行VideoReapeat视频解说复述克隆。 VideoReapeat视频解说复述克隆 是自研的AI工具箱Tauri版中的一款专用模块,旨在通过AI技术对视频解说内容进行复述和克隆。该工具可自动洗稿并重新生成视频解说,通过简单配置即可对大…...

MySQL5.7.42高可用MHA搭建及故障切换演示
系列文章目录 rpmbuild构建mysql5.7RPM安装包 MySQL基于GTID同步模式搭建主从复制 文章目录 系列文章目录前言一、MHA架构介绍1.MHA的功能2.MHA组成3.MHA故障转移过程4.MHA架构优缺点 二、环境准备1.服务器免密2.基于GTID主从复制搭建3.下载mha组件 三、MHA组件安装1.安装依赖…...

快速搭建最简单的前端项目vue+View UI Plus
1 引言 Vue是一套用于构建Web前端界面的渐进式JavaScript框架。它以其易学易用、性能出色、灵活多变而深受开发者喜爱,并且与其他前端框架(如React和Angular)相比,在国内市场上受到了广泛的认可和使用。点击进入官方…...

倍增练习(1)
A - ST 表 && RMQ 问题 题目思路:st表的板子题用于静态区间求最值,通过倍增的思想,先通过预处理将各个区间的最大值通过转移式求出f[i][j] max(f[i][j - 1], f[i (1 << (j - 1))][j - 1]);然后再进行重叠查询查询,k log2(r - l 1);,max(f[l][k], f[r - (1 &l…...

MATLAB 在数学建模中的深入应用:从基础到高级实践
目录 前言 一、MATLAB基础知识 1.1 MATLAB工作环境简介 1.1.1 命令窗口(Command Window) 1.1.2 工作区(Workspace) 1.1.3 命令历史(Command History) 1.1.4 编辑器(Editor) 1…...

Unity 设计模式 之 【什么是设计模式】/ 【为什么要使用设计模式】/ 【架构和设计模式的区别】
Unity 设计模式 之 【什么是设计模式】/ 【为什么要使用设计模式】/ 【架构和设计模式的区别】 目录 Unity 设计模式 之 【什么是设计模式】/ 【为什么要使用设计模式】/ 【架构和设计模式的区别】 一、简单介绍 二、 Unity 设计模式 1、Unity 开发中使用设计模式的特点 2…...

[数据集][目标检测]智慧交通铁路异物入侵检测数据集VOC+YOLO格式802张7类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):802 标注数量(xml文件个数):802 标注数量(txt文件个数):802 标注类别…...

飞驰云联FTP替代方案:安全高效文件传输的新选择
FTP协议广泛应用各行业的文件传输场景中,由于FTP应用获取门槛低、使用普遍,因此大部分企业都习惯使用FTP进行文件传输。然而面临激增的数据量和网络安全威胁的不断演变,FTP在传输安全性与传输性能上有所欠缺,无法满足企业现在的高…...

Hive内置集合函数-size,map_keys,map_values,sort_array,array_contains
1. Hive内置Collection Functions 以下函数为Hive是提供的内置集合函数: 返回类型函数(签名)函数说明intsize(Map<K.V>)Returns the number of elements in the map type.intsize(Array)Returns the number of elements in the array type.arraymap_keys(Map<K.V>…...

Exchange Online 计划 2 部署方案
目录 前言 一、前期准备 1. 了解 Exchange Online 计划 2 的功能 2. 系统要求 3. 网络要求 4. 账户和许可 二、安装和配置 Exchange Online 计划 2 1. 注册 Microsoft 365 订阅 2. 验证域 3. 用户和许可证分配 4. 迁移现有邮箱 迁移步骤 三、配置 Exchange Online …...
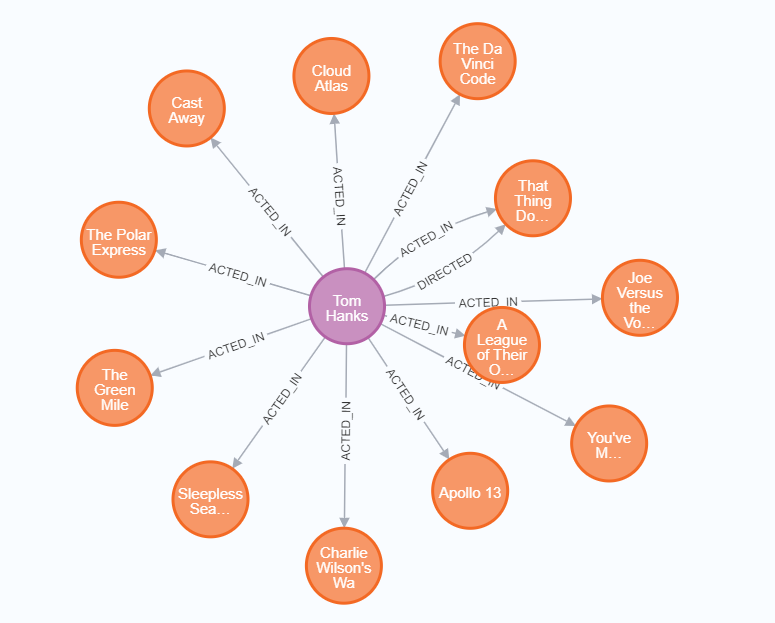
图数据库的力量:深入理解与应用 Neo4j
图数据库的力量:深入理解与应用 Neo4j 文章目录 图数据库的力量:深入理解与应用 Neo4j1、什么是 Neo4j?版本说明 2、Neo4j 的部署和安装Neo4j Web 工具介绍 3、体验 Neo4j加载数据查询数据数据结构 4、Cypher 入门创建数据查询数据关系深度查…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
