一文彻底让你搞懂轨迹规划(总结)
机器人在运行中不可避免的会进行运动,那么就会产生出轨迹规划的概念。
轨迹规划的特点:用一定的函数形式表示控制量(位置,速度,加速度)的控制律,根据约束或最优目标,求取控制控制参数。也就是利用数学的方法把一些物理量进行联系起来。
前言:
而常常口头说的轨迹规划又分为路径的规划和轨迹规划
路径规划:是指起点和终点所构成的路径而使用的策略。比如直线差补,圆弧差补,B样条,非均匀5次B样条,A*,D*,RRT等等。形象的来说,比如机器人要从a移动到b,那么他们之间的路径可以是直线的,圆弧的,曲线的等等。
同时这里在机器人中又可以分出一大类,这里不详细介绍了,具体有什么算法,大家可以看看下面我放的链接。
目标:路径规划的目标是使路径与障碍物的距离尽量远同时路径的长度尽量短;
轨迹规划:是指赋予了路径时间信息,比如在某一点处的速度,加速度应该是什么样子的,比如3-4-5多项式,T型,余弦,7段S型,15段S型,摆线等等,比如比如机器人要从a移动到b,如果更快并平滑的运行到终点。
目标:轨迹规划的目的主要是机器人关节空间移动中使得机器人的运行时间尽可能短,或者能量尽可能小。
注意:轨迹规划既可在关节空间也可在直角空间中进行,但是做规划的轨迹函数都必须连续和平滑,使得操作臂的运动平稳。即
同时也衍生出了两个:
- 笛卡尔轨迹规划 :注重点是机器末端的行走轨迹,是直线形还是圆弧形
- 关节空间轨迹规划 :注重点是关节的位置,速度,加速度,不能保证末端按照特定的路径。

具体使用?
使用的话有3种
1、只关心末端执行器行走的路径,比如直线,圆弧等,此时可以使用路径规划的算法,缺点是,不能保证关节电机的性能,有极大的可能超过电机速度,加速度的阈值。
2、只关心点到点之间平滑的运行,宏观上看整个机器人运行非常丝滑,缺点是,不能保证末端是怎么运行的,可能是直线,可能是曲线,也可能是乱七八糟的曲线,没有规律可言。
3,既关心末端执行器的路径,又关心机器平滑运行,所以要使用以上两种方法结合起来进行使用。比如在直线插补中使用345次多项式进行控制机器。
下面就单独介绍一下常见的规划方法,并且结合使用的基本要求是就利用轨迹规划算出路径的曲线,并根据相同的间隔时间计算出两个点之间的坐标,之后利用速度规划的方法进行计算。提高性能。
下面是点与点之间的位置关系,也可以叫做轨迹规划。(除了B样条,B样条是可以位置规划和速度规划联合起来的)
直线插补:
一般来说按着相同的时间步长来计算出差补的间隔或者是单位间隔,前提是规定此段走的时间,已知2个点的坐标,可以求出之间的距离(二维,三维空间都一样),距离除以间隔等于插补次数,利用公式可以求出相同间隔时间下的坐标,比如x =x0+单位*t ,得到了坐标,通过机器人的逆解就可以求出不同时刻下的关节角度。
圆弧差补:
二维:三个点确定一个圆弧,利用几何关系求出圆的圆心和半径,之后分别求出点1与点2之间的角度theta1,点1和点3之间的角度theta2,利用总时间分割出单位时间和差补个数,并求出每一个单位时间所走的单位弧度或单位距离,利用弧度变化值来求解圆弧上的点,得到点p,之后利用逆解进行求解机器人的各个关节角度。
三维:三维空间中需要新建立一个转换坐标系,为后期进行转换,求出圆心和半径,之后利用圆心(在转换坐标系中)和原点(基坐标系)的关系求出齐次变换矩阵,总时间设定,时间间隔也定,所以插补次数也已知,次数已知可以求出单位弧度,根据时间不断按照相同的时间间隔走,所以圆弧也是已知的,根据逆解求出各个关节的角度。
B样条:B样条又称一步规划。
根据多少个控制点,选用多少次的样条,确定好使用多少次的样条,可以根据控制点个数和多少次样条求出节点数,根据节点数不同的定义可以分为均匀B样条和标准均匀B样条和非均匀B样条等等,这里需要注意的一点是,原则上b样条的次数 = 控制点个数 - 1,但是当控制点很多的情况下,由于B样条的计算量很大,所以会选用低次样条来进行规划。知道了节点个数和值,利用基本公式求出每一个基函数,最终得到整个B样条公式,因为B样条最终得到的是关于时间t的通式,那么根据相同的时间间隔,就可以得到在此时的xyz等坐标。通过逆解可以求出各个关节的角度,并且该可以根据公式求出此位置的速度,加速度信息。
因为B样条最后的同时也是类似于多项式的,所以可以对速度和加速度进行限制。
所以B样条不断满足了让机器末端保持合理曲线的运动也保证了关节也是平滑运行,还可以进行限制。
【自动驾驶】运动规划丨轨迹规划丨算法综述分享_轨迹规划算法-CSDN博客文章浏览阅读186次。规划(planning)承接,并下启车辆控制。其规划出来的轨迹是带速度信息的路径。广义上,规划(planning)可分为。:是全局路径规划,可简单的理解为传统地图导航+高精地图(包含车道信息和交通规则等);:决策车辆是否跟车、在遇到交通灯和行人时的等待避让、以及路口和其他车辆的交互通过;:是局部路径规划,是在未来一段时间内的期望行驶路径,需满足汽车运动学、动力学、舒适性和无碰撞等要求。的任务是计算出一个无碰撞可执行的轨迹(包含路径和速度信息),保证车辆从起点安全的驾驶到目的地,并尽可能高效。_轨迹规划算法https://blog.csdn.net/tjcwt2011/article/details/141606280?spm=1001.2014.3001.5502
注意哈,以下是点到点之间的速度关系,保证了电机平滑运行,也可以叫做速度的轨迹规划
3-4-5多项式
五次多项式的通式子是:
(注意:3次多项式控制的是4个变量,起始点的位置速度和终止点的位置和速度,5次多项式控制6个,起始点的位置速度和加速度,终止点的位置速度和加速度)

对其进行一次求导和二次求导,得到关于速度和加速度的通式。如果要实现在5次多项式的情况下限制加速度,那么对加速度的3阶通式再一次求导,取极值(三阶导有一个极大值和一个极小值),之后就可以进行限制了。同理,3次也可以。最终得到,关于amax的式子。


T型:
顾名思义,T型就是说速度的曲线类似于梯型,包含了3个过程,加速过程,匀速过程和减速三个过程。主要是对速度进行分析,通常给定位置点和速度


 S型 :
S型 :
点到点轨迹规划——三次曲线,五次曲线,梯形曲线,S曲线-CSDN博客文章浏览阅读6.2w次,点赞73次,收藏570次。一. 简介点到点的轨迹规划算法可以理解为在规定的时间T内,从已知起始点运动到末尾点的方法。这里引入中间变量s(t),它是时间的函数,定义域为[0,T],值域为[0,1],s与的关系见下面公式。这个公式不难理解,当s=0时,;当s=1时,。对t求导是速度,即:对t求二阶导是加速度,即所以由于和是已知的,所以速度和加速度随时间的变化取决于..._五次曲线https://blog.csdn.net/fengyu19930920/article/details/81043776?spm=1001.2014.3001.5502 S型规划的“S”单指加速阶段的速度轮廓,整个S规划分为7个阶段:加加速、匀加速、减加速、匀速、加减速、匀减速、减减速。其中加加速、匀加速、减加速,三个阶段的曲线合在一起像英文字母S。(绿色曲线的前半部分,蓝色的是加速度,红色为加加速度):S规划相对于T规划,加减速更加平稳,对电机和传动系统的冲击更小,但是在相同的期望速度下,运动同样的距离所需的时间更长。

 余弦型:
余弦型:


抛物线轨迹:
4-25基本一维轨迹规划-2阶_哔哩哔哩_bilibili4-25基本一维轨迹规划-2阶, 视频播放量 879、弹幕量 1、点赞数 16、投硬币枚数 6、收藏人数 16、转发人数 3, 视频作者 每一天都应不同, 作者简介 ROS1是DCS,ROS2是FCS,相关视频:4-30复合一维轨迹规划-双S速度轨迹,4-24基本一维轨迹规划-1阶,4-27基本一维轨迹规划-5阶,4-28基本一维轨迹规划小结,6-13轨迹规划的Matlab仿真,3-3DH法建坐标系,7-2机器人控制系统的基本结构,6-1路径描述及轨迹生成,4-0动力学涉及的部分数学基础知识,4-37移动机器人平面运动轨迹规划方法-反馈控制法示例1![]() https://www.bilibili.com/video/BV1MN411G7Wx/?p=73&spm_id_from=pageDriver
https://www.bilibili.com/video/BV1MN411G7Wx/?p=73&spm_id_from=pageDriver
使用2个二阶的函数进行合成。两个二阶的可以保证在起始和终止点缓慢的加速,相对来说加速度是相对来说是小的。须知道初始和结束点的时间和位置,同时如果是任意的位置时间tf也需要知道。
注:机器人关节的加速度突变,对于电机来说会有一个冲击的。
问:为什么不用一个呢,因为一个抛物线的话始终在初始点或终止点这二点处存在一个最大加速度,可能会导致电机损伤等。




摆线运动
摆线运动的话,根据公式可以知道在某一时刻的速度加速度等信息。所表现的是点与点之间的运动情况,并非路径。


额外补充:
拉梅曲线:是一种运动路径 。
椭圆曲线:也是一种运动路径 。

举个例子
说了这么多,现有有一个让机器末端进行直线运行的,并保证要在规定的时间运行到位,这样实现了没有使用动力学而实现极高性能。
1.首先是确定目标点有几个,假如有1个目标点是home点,那么对于机器人来说要根据编码器的绝对位置求出当前的坐标。
2.知道了2个点,即目标点和当前位置点,就可以求出他们之间的距离了。并且给出运行此段的时间,假如为3s,但是假如有第二个控制点的话,有一个混合时间t,这个时间是T形曲线运行中的总时间,就可以根据位移公式求出最大的加速度了。注意这里并非0.5,而是5.7735是因为用了近似于s曲线的速度规律,使加速度真正的达到了最大值。
3.利用home的x坐标减去起始点的x轴坐标后除以总距离等于了在x轴上的单位距离。
4.并且利用总时间*1000/2ms = 插补次数,2ms是周期,也就是在这一段路程的时间间隔。
5.之后,在定义一个变量a,a在2ms周期是加1操作,直到a小于总的插补次数停止。
6.那么在2ms内的加1操作还了那些步骤,首先计算出了当前的时间,即2ms * 当前的插补次数 /1000。
7.求出当前时间占总时间(周期)的比例,也就是可以等换成位移,总时间 = 设定时间+混合时间
8.利用公式进行求解,ms,mv,ma。(公式是5次多项式,具体看上面的)
9.要移动的坐标是在2ms内 等于起始位置+ms*单位位置。
10.通过机器人的逆解,求出相应的关节电机应当转动多少角度。
11.通过一些电机驱动进行驱动电机,达到指定位置,依次类推,直到运行到home点。
注意:混合时间通常用于实现平滑的加速和减速,使得系统在起点和终点处的速度和加速度能够平滑过渡。
注意
实际的代码我就不放上去了,涉及到一些公司机密,不太方便,但是网上也有好多一样的代码,拿过来用。
以上的过程运用了直线差补和345次多项式结合的使用,也可以说是两步规划,而如果应用B样条,就可以直接求出位置点和速度,加速度的关系。
相关文章:

一文彻底让你搞懂轨迹规划(总结)
机器人在运行中不可避免的会进行运动,那么就会产生出轨迹规划的概念。 轨迹规划的特点:用一定的函数形式表示控制量(位置,速度,加速度)的控制律,根据约束或最优目标,求取控制控制参…...
)
windows C++ 并行编程-异步消息块(二)
overwrite_buffer 类 concurrency::overwrite_buffer 类与 unbounded_buffer 类类似,只不过 overwrite_buffer 对象仅存储一条消息。 此外,当目标接收来自 overwrite_buffer 对象的消息时,不会从缓冲区中删除该消息。 因此,多个目…...

【软件基础知识】什么是 API,详细解读
想象一下,你正在使用智能手机上的天气应用。你打开应用,瞬间就能看到实时天气、未来预报,甚至是空气质量指数。但你有没有想过,这些数据是如何神奇地出现在你的屏幕上的?答案就在三个字母中:API。 API,全称Application Programming Interface(应用程序编程接口),是现代软件世…...
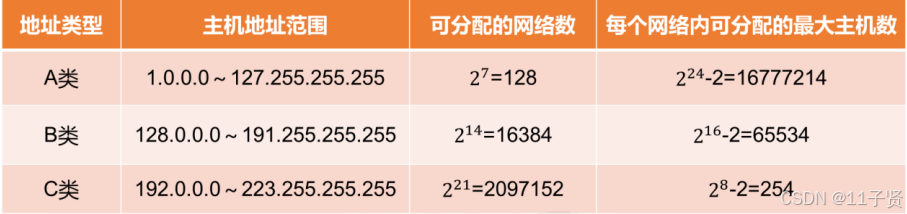
计算机四级-计算机网络
一、基础知识 1.对计算机网络发展具有重要影响的广域网是:ARPANET 随机争用型的介质访问控制方法起源于:ALOHANET 2.计算机网络发展阶段: A)第一阶段的主要成果是计算机技术与通信技术的结合 B)第二阶段的主要成果…...

【linux 获取时间】
linux 获取时间接口 我们在开发调试过程中,可能遇到一些和调用时序相关的问题,为了查看哪个步骤先调用,哪个步骤后调用,我们可以使用函数打印或者主动trace堆栈…但是有的时候我们需要排查2个接口调用的时间间隔,我们可…...

Dockerfile部署xxljob
使用Dockerfile部署xxljob 1. 背景 我们在使用定时任务调度时,通常会使用xxljob容器化部署xxljob,通常使用 docker pull xuxueli/xxl-job-admin:2.4.0 拉取镜像并启动容器。这种方式对于x86架构服务器来说,没有任何问题。但是在arm架构的服…...

Conda新建python虚拟环境问题
Conda新建python虚拟环境问题: 【问题1】 conda create --name yolov8 python3.10 -y Retrieving notices: …working… done Channels: defaults Platform: win-64 Collecting package metadata (repodata.json): failed UnavailableInvalidChannel: HTTP 404 NO…...
这几个优秀的工具网站真心值得推荐——搜嗖工具箱
即时工具 https://www.67tool.com/ 这是一个专注提升效率的办公工具网站;这也是一个拥有260多款自研在线工具和200多个客户端离线工具的服务网站;这还是一个可以满足包括视频处理、音频处理、图片处理、文档处理、文档转换、办公辅助、图表生成、文本工…...
ESP32开发 -- VSCODE+PlatformIO环境安装
参看官网安装:PlatformIO IDE for VSCode 一、安装PlatformIO IDE 参看:日常生活小技巧 – Visual Studio Code 简单使用 扩展中搜索platformIO IDE 当安装完提示重启之后。 打开一个要创建新工程的文件夹: 点击 Create New Project&…...

MySQL--导入SQL文件(命令行导入)
MySQL--导入SQL文件 一、前言二、导入SQL文件 一、前言 用可视化编辑工具编写,并且在控制台输入命令行在MySQL中导入SQL文件。 在导入SQL文件之前查看了目前存在的数据库 **目标:**在可视化编辑工具(这里以word文档为例)中编写SQL语句&…...

【C#基础】函数传参大总结
目录 前言参数是值类型的情况1. 按值传递(Pass by Value)2. 按引用传递(Pass by Reference)使用 ref使用 in 3. 输出参数传递(Output Parameters)参数修饰符对比小结 参数是引用类型的情况1. 按值传递类对象…...
初学51单片机之IO口上下拉电阻相关
本案本来是描述一下I2C总线的,在此之前推荐一下B站一个UP关于时序图的讲解 I2C入门第一节-I2C的基本工作原理_哔哩哔哩_bilibili 不过在描述I2C前先简单的探讨下51单片机IO口下拉电阻的基本情况,事实上这个问题困扰笔者很长时间了,这次也是一…...

Resnet50网络——口腔癌病变识别
一 数据准备 1.导入数据 import matplotlib.pyplot as plt import tensorflow as tf import warnings as w w.filterwarnings(ignore) # 支持中文 plt.rcParams[font.sans-serif] [SimHei] # 用来正常显示中文标签 plt.rcParams[axes.unicode_minus] False # 用来正常显示负…...

Python 中自动打开网页并点击[自动化脚本],Selenium
要在 Python 中自动打开网页并点击第一个 <a> 标签,你需要使用 Selenium,它可以控制浏览器并执行像点击这样的操作。requests 和 BeautifulSoup 只能获取并解析网页内容,但不能进行网页交互操作。 步骤: 安装 Selenium安装…...

Spring Boot-自动配置问题
**### Spring Boot自动配置问题探讨 Spring Boot 是当前 Java 后端开发中非常流行的框架,其核心特性之一便是“自动配置”(Auto-Configuration)。自动配置大大简化了应用开发过程,开发者不需要编写大量的 XML 配置或是繁琐的 Jav…...

CS61B学习 part1
本人选择了2018spring的课程,因为他免费提供了评分机器,后来得知2021也开放了,决定把其中的Lab尝试一番,听说gitlab就近好评,相当有实力,并借此学习Java的基本知识,请根据pku的cswiki做好评分机…...

我Github的问题解决了!
看的这篇,解决使用git时遇到Failed to connect to github.com port 443 after 21090 ms: Couldn‘t connect to server_git couldnt connect to server-CSDN博客 之前想推送的能推送了,拉取的也能取了。 一、如果是在挂着梯子的情况下拉取或者推送代码…...

Pytorch构建神经网络多元线性回归模型
1.模型线性方程y W ∗ X b from torch import nn import torch#手动设置的W参数(待模型学习),这里设置为12个,自己随意设置weight_settorch.tensor([[1.5,2.38,4.22,6.5,7.2,3.21,4.44,6.55,2.48,-1.75,-3.26,4.78]])#手动设置…...

如何基于Flink CDC与OceanBase构建实时数仓,实现简化链路,高效排查
本文作者:阿里云Flink SQL负责人,伍翀,Apache Flink PMC Member & Committer 众多数据领域的专业人士都很熟悉Apache Flink,它作为流式计算引擎,流批一体,其核心在于其强大的分布式流数据处理能力&…...

ActiveMQ、RabbitMQ 和 Kafka 在 Spring Boot 中的实战
在现代的微服务架构和分布式系统中,消息队列 是一种常见的异步通信工具。消息队列允许应用程序之间通过 生产者-消费者模型 进行松耦合、异步交互。在 Spring Boot 中,我们可以通过简单的配置来集成不同的消息队列系统,包括 ActiveMQ、Rabbit…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
