进制数知识(2)—— 浮点数在内存中的存储 和 易混淆的二进制知识总结
目录
1. 浮点数在内存中的存储
1.1 浮点数的大V表示法
1.2 浮点数的存储格式
1.3 浮点数的存入规则
1.4 浮点数的读取规则
1.5 补充:移码与掩码
1.6 题目解析
2. 易错的二进制知识
2.0 符号位到底会不会参与运算?
2.0.1 存储前的编码变化运算
2.0.2 存储后的数值算术运算
2.1 整数都以补码进行存储和运算 & 整型提升的2种情况
2.1.1 存储前的整型提升 与 补码
2.1.2 运算时的整型提升 与 补码(补码的运算)
2.3 unsigned对数据的本质影响
2.3.1 unsigned控制读取方式(打印方式),不控制数据的存储
2.3.2 unsigned控制运算时的整型提升
2.3.3 易错:用%u打印char型数据,不代表该数据被unsigned修饰
2.4 图示总结
1. 浮点数在内存中的存储
常⻅的浮点数:3.14159、1E10等,浮点数家族包括: float、double、long double 类型。 浮点数表⽰的范围在 float.h 中定义
1.1 浮点数的大V表示法
根据国际标准IEEE(电⽓和电⼦⼯程协会)754,任意⼀个⼆进制浮点数V可以表示成下⾯的形式:
- (−1)^S 表示符号位。当S=0,V为正数;当S=1,V为负数。
- M 表示有效数字,M大于等于1,小于2。(1 <= M < 2)
- 2^E 表示指数位。
其实这个公式就是二进制的科学计数法,这与十进制的科学计数法类似( (-1)^S * M * 10^E )
举例来说:
(1)十进制的5.0,写成⼆进制是:101.0 ,相当于 1.01×2^2 。
那么,按照大V表示法的格式,可以得出S=0,M=1.01,E=2。
(2)⼗进制的-5.0,写成⼆进制是 -101.0 ,相当于 -1.01×2^2 。
那么,S=1,M=1.01,E=2。
(3)十进制的0.25,写成二进制是 0.01,相当于 1× 2^(-2)
那么,S=0,M=1.0,E= -2。
1.2 浮点数的存储格式
IEEE 754规定,对于32位的浮点数(float):
(1)最高的1位存储符号位S
(2)接着的8位存储指数位E
(3)剩下的23位存储尾数位M

IEEE 754规定,对于64位的浮点数(double):
(1)最高的1位存储符号位S
(2)接着的11位存储指数位E
(3)剩下的52位存储尾数位M

long double类型通常占用更多的内存空间,一般是10到12个字节(80到96位),但在某些系统上可能达到16个字节(128位)。这里不多做解释。
1.3 浮点数的存入规则
IEEE 754 对于有效数字M和指数E,还有⼀些特别规定。
M的存入规则:
- 前⾯说过1≤M<2 。也就是说,M可以写成 1.xxxxxx 的形式,其中 xxxxxx 表示小数部分。
- IEEE 754 规定,在计算机内部保存M时,默认这个数的第⼀位总是1,因此可以被舍去,只保存后面的 xxxxxx 部分。
⽐如保存1.01的时候,只保存01,等到读取的时候,再把第⼀位的1加上去。
这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位,将第⼀位的1舍去以后,等于可以保存24位有效数字。
E的存入规则:
- 首先,E为⼀个无符号整数(unsigned int)。
这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。但是科学计数法中的E是可以出现负数的。
- 所以IEEE 754规定,存⼊内存时E的真实值必须再加上一个中间数(偏移量)。
- 对于8位的E,这个中间数是127;(2的8次方是256,255 / 2 == 127)
- 对于11位的E,这个中间数是1023。(2的11次方是2048,2047 / 2 == 1023)
⽐如,2^10的E等于10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
1.4 浮点数的读取规则
由于指数E有特殊情况,M的读取也跟着不一样:(主要分为三种情况)
1. E的存入值不全为0或不全为1(一般情况)
- 指数E的存入值减去127(或1023),得到真实值。
- M的读取:得到真实值后,再将小数部分(尾数位)前加上第⼀位的1,变回1.xxxxxx 的形式。
⽐如:
十进制数0.5 的⼆进制形式为0.1,大V表示法为1.0 * 2^(-1)
其指数位E为-1+127(中间值)=126,存入为01111110
而尾数位M是1.0,去掉整数部分为0,补⻬0到23位 00000000000000000000000,则其⼆进制表示形式为:
0 01111110 00000000000000000000000
2. E的存入值全为0
如果是2^(-127)的话,这个数太小了,无限接近0。由于这样的数字精度不太够,IEEE 754规定:
- M的读取:尾数位不再加上第一位的1,⽽是当作为 0.xxxxxx 的小数来约分处理。
- 规定指数E等于 -126(或者-1022)即为真实值。
该情况下的3种意义:这样做是为了表示±0,以及接近于0的数字。
- +0:符号位为0,8个(或11个)指数位为全为0,23个(或52个)尾数位全为0。
- -0:符号位为1,8个(或11个)指数位为全为0,23个(或52个)尾数位全为0。
- 接近0的数字:8个(或11个)指数位为全为0,尾数位不全为0。
解析:
你可以理解成:有效数字从1.xxxxxx 变成了 0.1xxxxx 的形式,既然有效数字向右退位了,那么指数部分就要+1补位,所以E的真实值是1-127(或者1-1023)。
3. E的存入值全为1
如果是2^(128)的话,这个数太大了。这样的数字精度也不太够,IEEE 754规定:
- M的读取:此时尾数位也不进行添1操作。
- 此时真实值E无效。
该情况下也有三种意义:
- 正无穷(+∞或+inf):符号位为0,指数位全为1,尾数位全为0。
- 负无穷(-∞或-inf):符号位为1,指数位全为1,尾数位全为0。
- 不存在的数字(NaN,Not a Number):指数位全为1,尾数位存在1。
1.5 补充:移码与掩码
还有几点我想要补充一下:
补充1:
- 浮点数指数位的存储和运算,使用的不是原码、反码和补码,而是移码(“偏移量”或“偏移二进制编码”)。
补充2:
- 移码的运算规则:用二进制存储偏移后的E,用十进制来计算真实值的E。
- 指数位虽然是无符号整型,但由于移码运算的特殊性(二进制存储,十进制计算),所以指数位不会发生数据截断。
举个例子:
假如在float型中,E的真实值是-2,存入的过程并不是:
- 1111 1110 (-2的补码) + 0111 1111 (127的补码) 得到1 0111 1101,再截断多出的1位,变成0111 1101 (125的补码)
而是这样:
- 存入时的10进制计算:-2+127=125
- 以2进制存入:111 1101 (-2的移码)(这个就是数学上的二进制数字,并不是原码,反码或补码)
- 取出时的10进制计算:先读取:111 1101 (2进制数字) == 125 (10进制数字);再计算:125 -127 = -2
补充3:
(1)尾数位M的存入:
尾数位采取掩码的方式存储。在计算机科学中,掩码通常是一个二进制序列,用来选择或隐藏特定的数据位。在浮点数的尾数位中,中隐藏了有效数字的1 。
(2)尾数位的大小:
还没补回1的尾数位序列,从左向右,位数依次减少,最高位是2的-1次方。
补充4:
浮点数的计算器 与 整数的计算器是不同的。
(浮点数运算器被设计出来专门处理带有小数点的数值,采用不同的运算方式,这也是移码和掩码存在的意义 以及 移码运算性质不同的原因)
1.6 题目解析
判断下面这段代码会输出什么:
int main()
{int n = 9;float *pFloat = (float *)&n;printf("n的值为:%d\n",n);printf("*pFloat的值为:%f\n",*pFloat);*pFloat = 9.0;printf("num的值为:%d\n",n);printf("*pFloat的值为:%f\n",*pFloat);return 0;
}代码结果:

这种情况出现的本质是,存储的方式与读取的方式不匹配。
代码的上半部分中,整数9存入了整型变量n中,它的二进制编码是:
00000000 00000000 00000000 00001001(9的补码)
- %d是以整数的方式读取内存(以补码的方式读取),读取的结果就是9。
- %f 是以浮点数的方式读取内存(以移码+偏码的方式读取),由于指数位全是0,且尾数位太小精度不够(默认显示6位小数),所以显示的是0.000000。
代码的下半部分中,通过指针把浮点数9.0存入n的内存空间中,其二进制编码是:
【大概的样子】0 01111110 111001100110011001000000
( 0.9无法用二进制完全表示,约等于1.111 * 2^(-1) )
- %d当做整数去读取,这里最高的二进制位已经是2^30了,所以最终结果是一个很大的整数。
- %f 就正常读取一个浮点数,所以结果是9.000000。
2. 易错的二进制知识
2.0 符号位到底会不会参与运算?
我们知道,为了表示区分正负数,规定了数据类型的最高位二进制位为符号位。又由于计算机只有加法器,没有减法器,我们创造了补码。
原码的符号位和补码的符号位是一样的,那么符号位其实会不会参与运算呢?
这得分两种情况讨论:
2.0.1 存储前的编码变化运算
由原码得到补码的过程是:原码符号位不变,数值位按位取反得到反码,再对反码+1得到补码。
由补码得到原码的过程是:补码符号位不变,数值位按位取反得到补码的反码,再对该反码+1得到原码。
原码、反码、补码 相互转换,这些的过程就是编码变化运算。
我们注意到:由原码得到补码时,符号位并不会发生变化而且该运算发生在数据存储到内存空间之前。所以编码变化运算中的符号位并不会真实参与运算。
计算机执行该运算的硬件是逻辑单元(ALU)。当需要将一个数的原码转换为补码时,计算机会检查原码的最高位(符号位),如果符号位为0(表示正数),则原码与补码相同;若符号位为1(表示负数),则需要将除符号位外的其他位取反(即0变为1,1变为0),然后整体加1。
2.0.2 存储后的数值算术运算
在数据保存在内存空间后(或暂存到内存后),此后的一系列算术运算,符号位会真实参与到算术运算当中。
比如,我们用char计算2-1的结果:a = 2 - 1。
第一步:存储数据
2和-1的数据会暂存到加法器的内存中,由于没有减法器,我们采用的是补码的加法。
2的char大小的型补码是00000010;-1的char型大小的补码是11111111。
第二步:存储后的整型提升
由于char型数据太小,计算机会自动将他整型提升成int型大小的数据,按符号位提升。(紫色是提升后的字节,红色是char型数据的符号位)
整型提升后2的补码:00000000 00000000 00000000 00000010
整型提升后-1的补码:11111111 11111111 11111111 11111111
第三步:算术运算
此时才正式进行算术运算,两个补码提升后的结果:(黄色是进位后的下一个字节)
1 00000000 00000000 00000000 00000001
由于右边第2个二进制位1+1等于2要进位,导致后面的所有二进制位都进位了,所以多出了第33位二进制位。
第四步:数据截断
因为a是char型数据,装不下5个字节大小的数据,所以数据截断只剩下低位字节,即:00000001
从第3步可以看到,符号位也真实参与了算术运算,上下0+1等于了1,因为前面的数字进1,所以符号位最终的结果是“1+1等于0”。
人们常说:数值运算时,符号位不计算,只计算数值位就行了。其实这么说也不算错,由于补码算术运算的特殊性,确实造就了这句话的现实意义。(误区的来源)
但这样理解无疑是片面的,符号位也会真实参与到算术运算当中。
2.1 整数都以补码进行存储和运算 & 整型提升的2种情况
2.1.1 存储前的整型提升 与 补码
补码的存储:
对于较小整型的存储(或初始化),会先用较大的数据类型,以原码的形式表示出该十进制数字的二进制形式。然后把该较大型数据从原码转换成补码。再对该二进制补码序列进行数据截断。
存储前的整型提升 的特性:
- 在创建字节数较小的变量时,系统默认会先开辟4个字节或8个的空间,即存储前的整型提升。
- 在默认内存空间中,符号位是该空间的最高二进制位。x86环境下,符号位是第32位;x64环境下,符号位是第64位。
- 数据截断后会产生新的符号位。
- 此时的整型提升不会被unsigned影响:数据是负数,最高位就是1;数据是正数,最高位就是0。
比如,我们要用char存储-10:char a = -10;
第一步:用int型空间和原码表示出该数字的二进制形式
-10的二进制原码表示:100000000 00000000 00000000 00001010 (红色的是符号位)
第二步:通过编码变化运算,转换成补码
转换为补码后的结果:11111111 11111111 11111111 11110110 (红色的是符号位)
第三步:数据截断,存入char型空间中
截断和存入的结果:11110110(新的符号位)
2.1.2 运算时的整型提升 与 补码(补码的运算)
补码的运算:
较小的整型会先对补码进行整型提升,再对提升后的结果进行运算。(提升后的每一个二进制位都会参与运算)
合适大小的整型可以直接对补码进行算术运算。
运算时的整型提升 的特性:
- 在字节数较小的数据运算时,会先进行整形提升,变成较大的数据。
- 会根据符号位进行补位提升。正数补0,负数补1。
- 此时的整型提升会被unsigned影响。
例子可以参考2.0.2的示例。
2.3 unsigned对数据的本质影响
2.3.1 unsigned控制读取方式(打印方式),不控制数据的存储
(1)对一个unsigned类型的变量赋值一个负数,不会因为unsigned修饰就让数据存储的最高位为0,仍然是正常地得储存。
(2)但以%u读取时会把符号位也当做数值位读取。
代码演示:
int main()
{unsigned int a = -1;printf("以有符号数的形式读取:%d\n", a);printf("以无符号数的形式读取:%u\n", a);
}
-1用二进制存储是:
11111111 11111111 11111111 11111111
以%d来读取,那就是-1;
以%u来读取,结果是2^32-1,即:4294967295。
2.3.2 unsigned控制运算时的整型提升
前面提到过,运算时的整型提升会被unsigned影响,具体是什么呢?
(1) 对于较小的unsigned整型,在运算时(存储后的数据),整型提升不再看最高位是0还是1,都统一用0来补位。
例如:
int main()
{unsigned char a = -1;printf("%u\n", a);return 0;
}
-1的存储仍然遵循 “原码表示二进制int型数字 ---> 转换为补码 ---> 数据截断” 的顺序。所以变量a中,-1的存储是11111111。
当以%u (unsigned int)的形式打印时,a的数据会先进行整型提升。而且a被unsigned修饰,整型提升是用0补位,变成:
00000000 00000000 00000000 11111111
所以结果是255。
2.3.3 易错:用%u打印char型数据,不代表该数据被unsigned修饰
我们用一段代码来演示:
int main()
{char a = 128;printf("%u\n", a);char b = -128;printf("%u\n", b);return 0;
}
过程解析:
第一步:原码表示
128的原码表示:00000000 00000000 00000000 10000000
-128的原码表示:10000000 00000000 00000000 10000000
第二步:补码转换
128的补码不变:00000000 00000000 00000000 10000000
-128的补码:11111111 11111111 11111111 10000000
第三步:数据截断
128 和 -128都只剩下:10000000
第四步:打印前的整型提升
%u是unsigned int型,由于变量a和b都是char型,较小的整型就要进行整形提升
且它们都是char型,而不是unsigned char型,所以符号位仍然存在。
有符号位时,按符号位来补位,它们都变成:
11111111 11111111 11111111 10000000
(如果是该数据是unsigned型的,那么这里补的就是0,而不是1了)
第五步:打印
由于以%u的形式输出,打印的时候把最高位当作数值位读取,所以结果就是这么大的数字。
2.4 图示总结
小数据类型的存储:

小数据类型的运算和输出:
本期分享完毕,感谢大家的支持~Thanks♪(・ω・)ノ

相关文章:

进制数知识(2)—— 浮点数在内存中的存储 和 易混淆的二进制知识总结
目录 1. 浮点数在内存中的存储 1.1 浮点数的大V表示法 1.2 浮点数的存储格式 1.3 浮点数的存入规则 1.4 浮点数的读取规则 1.5 补充:移码与掩码 1.6 题目解析 2. 易错的二进制知识 2.0 符号位到底会不会参与运算? 2.0.1 存储前的编码变化运算 …...

类似QQ聊天功能的Java程序
实现一个类似QQ聊天功能的Java程序需要考虑以下几个关键点: 用户界面:用于展示消息和输入消息。网络通信:用于客户端之间的信息传输。用户管理:用于管理用户的登录、注册和状态。消息存储:用于存储聊天记录。 这里提…...

Redis 键值对数据库学习
目录 一、介绍 二、安装以及连接 三、设置连接密码 四、连接报错 五、redis 操作字符串以及过期时间 六、 redis 列表操作 七、redis 集合操作 八、hash 哈希操作 九、redis 发布和订阅操作 十、RDB和AOF的两种数据持久化机制 十一、 其他机器连接redis 十二、 pyt…...

逆向推理+ChatGPT,让论文更具说服力
学境思源,一键生成论文初稿: AcademicIdeas - 学境思源AI论文写作 使用ChatGPT辅助“逆向推理”技巧,可以显著提升论文的质量和说服力。逆向推理从结论出发,倒推所需的证据和论点,确保整个论证过程逻辑严密且无漏洞。…...

「JavaScript深入」一文说明白JS的执行上下文与作用域
JavaScript深入 — 执行上下文与作用域 上下文执行上下文生命周期创建阶段执行阶段回收阶段 执行栈作用域链作用域词法作用域(静态作用域) 上下文 变量或函数的上下文决定了它们可以访问哪些数据,以及它们的行为。 每个上下文都有一个关联的…...

Qt C++设计模式->组合模式
组合模式(Composite Pattern)是一种结构型设计模式,允许你将对象组合成树形结构以表示部分与整体的层次关系。组合模式使得客户端可以以统一的方式对待单个对象和组合对象,简化了对复杂树形结构的操作。 组合模式的应用场景 组合…...

Acwing Bellman-Ford SPFA
1. Bellman-Ford 该算法适用于有负权边的情况,注意:如果有负权环的话,最短路就不一定存在了。时间复杂度 O ( m n ) . O(mn). O(mn).该算法可以求出来图中是否存在负权回路,但求解负权回路,通常用SPFA算法,…...

我能禁止使用某协议的ip禁止访问我的资源吗
是的,你可以禁止使用某个协议的IP地址访问你的资源。这种操作通常涉及网络防火墙、服务器配置或应用程序设置,具体方法取决于你的网络环境和使用的技术。以下是一些常见的实现方法: 1. 使用防火墙 大多数防火墙(硬件或软件&…...
——TCP协议中的拥塞控制机制详解)
快速理解TCP协议(二)——TCP协议中的拥塞控制机制详解
在计算机网络中,TCP(传输控制协议)是一种广泛使用的面向连接的、可靠的、基于字节流的传输层通信协议。TCP协议通过一系列复杂的机制来确保数据的可靠传输,其中拥塞控制是至关重要的一环。本文将深入探讨TCP协议中的拥塞控制机制&…...

Linux:debug: systemtap: ubacktrace
https://docs.huihoo.com/systemtap/sourceware.org/systemtap/SystemTap_Beginners_Guide/ustack.html 这个函数可以帮助将user level的backtrace打印出来。 stap -d /bin/ls --ldd \ -e probe process("ls").function("xmalloc") {print_usyms(ubacktra…...
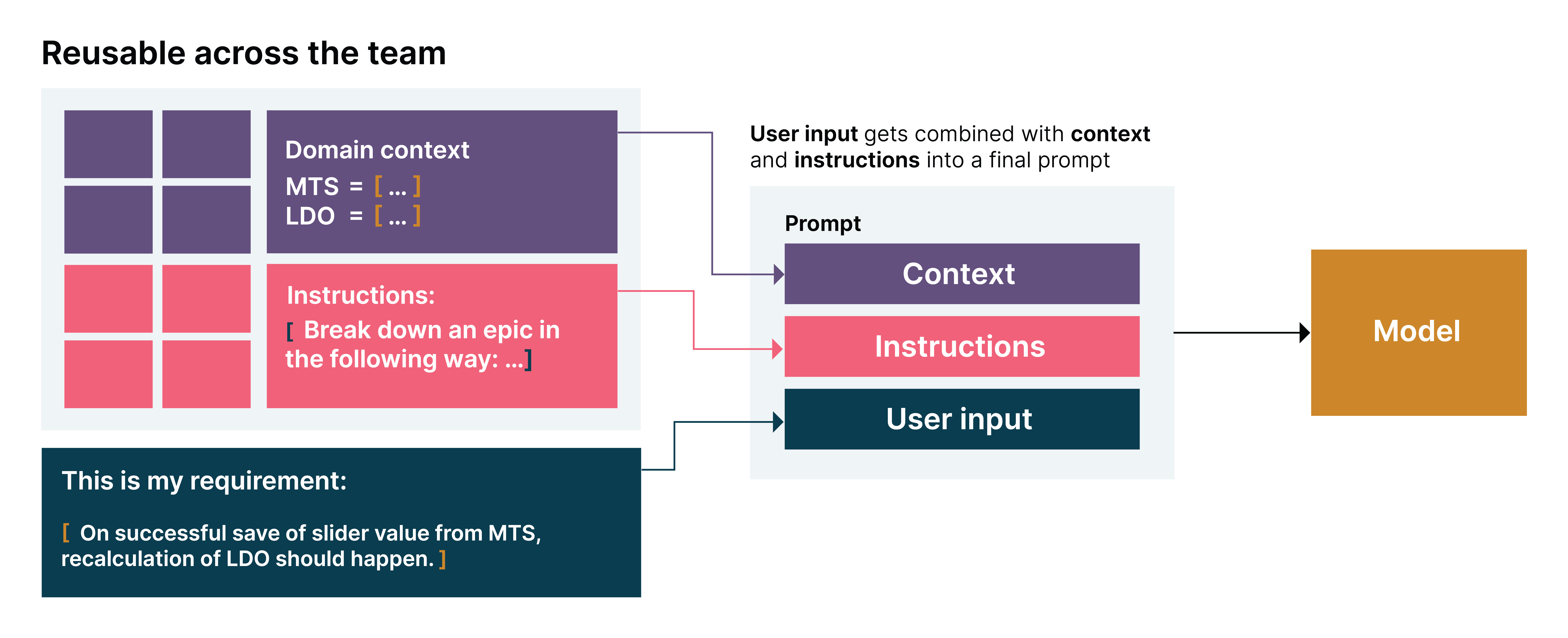
使用AI进行需求分析的案例研究
生成式 AI 的潜在应用场景似乎无穷无尽。虽然这令人兴奋,但也可能让人不知所措。因此,团队在使用这项技术时需要有明确的目标:关键是要明确生成式 AI 在团队工作中能产生哪些实质性影响。 在软件工程中,一个引人注目的应用场景是…...

Python内置的re库
Python内置的re库是专门用于处理正则表达式的标准库。它提供了一系列函数和类,使得在Python程序中可以使用正则表达式进行字符串的搜索、替换、分割等操作。re库的使用非常广泛,几乎任何需要复杂文本处理的场景都可以用到它。 主要函数 1、complie函数…...

毕业设计选题:基于ssm+vue+uniapp的面向企事业单位的项目申报小程序
开发语言:Java框架:ssmuniappJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:M…...

jQuery 简介⑤属性操作
九、属性操作 jQuery的属性操作方法一览表 $("selector").val(); // 获取第一个匹配元素的value值(一般用于表单控("selector").val("Hello"); // 设置所有匹配元素的value值为"Hello" $("selector").html();// 获取第一个…...

[Linux] Linux操作系统 进程的状态
标题:[Linux] Linux操作系统 进程的状态 个人主页:水墨不写bug (图片来源于网络) 目录 一、前置概念的理解 1.并行和并发 2.时间片 3.进程间具有独立性 4.等待的本质 正文开始: 在校的时候,你一定学过《…...

深入解析Python 中的 sortedcontainers 库:高效的排序数据结构
在日常的 Python 编程中,列表(list)、集合(set)和字典(dict)是常用的数据结构。然而,在某些特定的场景下,我们需要对数据进行排序,并且希望在插入、删除或访问…...

什么是服务器日志,日志有什么作用?
前言 服务器日志是指服务器等电脑设备或软件的运作记录。这些日志记录了服务器接收客户端处理请求的过程以及服务器对这些请求的处理结果。服务器日志对于排查和解决计算机系统和网络应用中的问题至关重要,因为它们包含了用于调试问题的消息、服务器状态以及其他…...
A-G1题解)
Codeforces Round 971 (Div. 4)A-G1题解
Codeforces Round 971 (Div. 4) A 就是b - a #include <bits/stdc.h> #define int long longusing namespace std;void solve() {int a, b;cin >> a >> b;cout << b - a << endl; }signed main() {ios::sync_with_stdio(false);cin.tie(0);co…...
QT----基于QML的计时器
赶上了实习的末班车,现在在做QML开发,第一天的学习成果,一个计时器.逻辑挺简单的,纯QML实现,代码在仓库,可以对比文档和提交记录学习起来更清晰 QT-Timer 学习使用c的listmodel 学习使用了如何用c的listmodel来存储数据. 新建一个TImeListModel类继承自QAbstractListModel c…...
)
Stable Diffusion的高分辨率修复(Hires.fix)
Stable Diffusion的高分辨率修复(Hires.fix)是一项重要的功能,它旨在提高生成图像的分辨率和细节,从而使画面变得更加清晰和精细。以下是关于Stable Diffusion高分辨率修复(Hires.fix)的详细解释࿱…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

