数据结构讲解二叉树 【一】
🎁🎁创作不易,关注作者不迷路🎀🎀
C语言二叉树 【一】
- 前言
- 一、数概念及结构
- 1.数的概念
- 1.2树的相关概念
- 1.3树的表示
- 二、二叉树的概念及结构
- 2.1
- 2.2二叉树的性质
- 2.3二叉树的存储结构
- 三、二叉树的顺序结构实现
- 3.1二叉树的顺序结构
- 3.2堆的概念及结构
- 3.3堆的实现
- 3.3.1堆向下调整算法
- 3.3.2堆的删除元素
- 3.3.3堆的插入元素
- 四、源码
前言

点点
点点
点点
点点
点点
点点
一、数概念及结构
1.数的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根结点没有前驱结点
- 除根结点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构

1.2树的相关概念

- 结点的度:一个结点含有的子树的个数称为该结点的度; 如上图:A的为6
- 叶结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I…等结点为叶结点
- 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
- 兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
- 树的度:一棵树中,最大的结点的度称为树的度; 如上图:树的度为6
- 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
- 树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
1.3树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType; struct Node {struct Node* firstChild1; // 第一个孩子结点 struct Node* pNextBrother; // 指向其下一个兄弟结点DataType data; // 结点中的数据域 };代码的实际示例图如下:
点点
点点
点点
点点
点点
点点
二、二叉树的概念及结构
2.1
这里我们主要介绍两种特殊的二叉树
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.2二叉树的性质

2.3二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
- 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
- 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* left; // 指向当前结点左孩子struct BinTreeNode* right; // 指向当前结点右孩子BTDataType data; // 当前结点值域
}// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* parent; // 指向当前结点的双亲struct BinTreeNode* left; // 指向当前结点左孩子struct BinTreeNode* right; // 指向当前结点右孩子BTDataType data; // 当前结点值域
};点点
点点
点点
点点
点点
点点
三、二叉树的顺序结构实现
3.1二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
3.2堆的概念及结构
如果有一个关键码的集合K = { k 0 k_0 k0, k 1 k_1 k1, k 2 k_2 k2,…, k n − 1 k_{n-1} kn−1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: K i K_i Ki <= K 2 ∗ i + 1 K_{2*i+1} K2∗i+1 且 K i K_i Ki<= K 2 ∗ i + 2 K_{2*i+2} K2∗i+2 ( K i K_i Ki >= K 2 ∗ i + 1 K_{2*i+1} K2∗i+1 且 K i K_i Ki >= K 2 ∗ i + 2 K_{2*i+2} K2∗i+2) i = 0,1,2…,则称为小堆(或大堆)。将根结点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。
堆的性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树。
3.3堆的实现
3.3.1堆向下调整算法
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根结点开始的向下调整算法可以把它调整成一个小堆。
向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
通过示意图展现向下调整过程:
// 左右子树都是大堆/小堆
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 选出左右孩子中大的那一个if (child + 1 < n && a[child+1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
3.3.2堆的删除元素
删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。

这里很多初学者都会有疑问,为什么我们在删除根节点后,不直接用他的儿子替代,一次挪动,这样不是更加方便吗?
我想,可以通过这张示意图来解答大家的困惑。首先,我们发现挪动看似逻辑简单,然而它带来了许多问题,,它直接改变了树的父子兄弟关系,在这时候,很有可能就不满足堆的概念了,不再是顺序结构了。void HeapPop(HP* php) { assert(php); assert(!HeapEmpty(php));// 删除数据 Swap(&php->a[0], &php->a[php->size - 1]); php->size--; AdjustDown(php->a, php->size, 0); }
3.3.3堆的插入元素
先插入一个10到数组的尾上,再进行向上调整算法,直到满足堆。
// 除了child这个位置,前面数据构成堆
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//while (parent >= 0)while(child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity*2);if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity *= 2;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}
四、源码
heap.c
#include "Heap.h"void HeapInit(HP* php)
{assert(php);php->a = (HPDataType*)malloc(sizeof(HPDataType)*4);if (php->a == NULL){perror("malloc fail");return;}php->size = 0;php->capacity = 4;
}void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType x = *p1;*p1 = *p2;*p2 = x;
}// 除了child这个位置,前面数据构成堆
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//while (parent >= 0)while(child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity*2);if (tmp == NULL){perror("realloc fail");return;}php->a = tmp;php->capacity *= 2;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}// 左右子树都是大堆/小堆
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 选出左右孩子中大的那一个if (child + 1 < n && a[child+1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));// 删除数据Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}HPDataType HeapTop(HP* php)
{assert(php);return php->a[0];
}bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}int HeapSize(HP* php)
{assert(php);return php->size;
}
text.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"//int main()
//{
// HP hp;
// HeapInit(&hp);
// HeapPush(&hp, 4);
// HeapPush(&hp, 18);
// HeapPush(&hp, 42);
// HeapPush(&hp, 12);
// HeapPush(&hp, 21);
// HeapPush(&hp, 3);
// HeapPush(&hp, 5);
// HeapPush(&hp, 5);
// HeapPush(&hp, 50);
// HeapPush(&hp, 5);
// HeapPush(&hp, 5);
// HeapPush(&hp, 15);
// HeapPush(&hp, 5);
// HeapPush(&hp, 45);
// HeapPush(&hp, 5);
//
// int k = 0;
// scanf("%d", &k);
// while (!HeapEmpty(&hp) && k--)
// {
// printf("%d ", HeapTop(&hp));
// HeapPop(&hp);
// }
// printf("\n");
//
// return 0;
//}
heap.h
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
//
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}HP;
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);
int HeapSize(HP* php);
void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a, int n, int parent);

相关文章:

数据结构讲解二叉树 【一】
🎁🎁创作不易,关注作者不迷路🎀🎀 C语言二叉树 【一】 前言一、数概念及结构1.数的概念1.2树的相关概念1.3树的表示 二、二叉树的概念及结构2.12.2二叉树的性质2.3二叉树的存储结构 三、二叉树的顺序结构实现3.1二叉树…...

MATLAB基础应用精讲-【数模应用】OR值
目录 前言 几个高频面试题目 or值越小代表什么 RR值、OR值及HR值的区别 算法原理 什么是OR值 OR值的计算方法和含义 注意事项 SPSSAU OR值和RR值 1、背景 2、理论 3、操作 4、SPSSAU 输出结果 5、文字分析 6、剖析 疑难解惑 SE(ln(OR)或SE(ln(RR)的意义? …...
[vulnhub] w1r3s.v1.0
https://www.vulnhub.com/entry/w1r3s-101,220/ 思路:红队笔记 主机发现端口扫描 使用nmap扫描网段类存活主机 因为靶机是我最后添加的,所以靶机IP是133 nmap -sP 192.168.75.0/24 // Starting Nmap 7.93 ( https://nmap.org ) at 2024-09-20 09:09 CST…...

c#中的功能优势
装箱和拆箱 性能消耗的直接体现 int iterations 10000000; // 进行一千万次迭代Stopwatch stopwatch new Stopwatch();// 非装箱测试stopwatch.Start();for (int i 0; i < iterations; i){int x i; // 纯值类型操作,无装箱}stopwatch.Stop();Console.Writ…...
Windows系统设置定时任务,周期性执行.bat文件
通过.bat清除注册表项 在 Windows 系统中,.bat 文件(批处理文件)是一个包含一系列命令的文本文件。这些命令会被 Windows 命令解释器 (cmd.exe) 依次执行。 你可以把它想象成一个简单的程序,但它不像 C 或 Python 那样需要编译&a…...

xQTLs 共定位分析(XQTLbiolinks包)
XQTL 共定位分析 XQTLbiolinks 是一个端到端的生物信息学工具,由深圳湾实验室李磊研究团队开发,用于高效地分析公共或用户定制的个xQTLs数据。该软件提供了一个通过与 xQTLs 共定位分析进行疾病靶基因发现的流程,以检测易感基因和致病变异。…...
)
网络工程(学习记录)
day1创建Vlan Switch>enable Switch#configure terminal Switch(config)#hostname SW1 修改名称为SW1 SW1(config)# SW1(config)#vlan 10 创建vlan10 SW1(config-vlan)#vlan 20 SW1(config)#interface f0/1 进入接口f0…...

全志A133 android10 适配EC20 4G模块
一,移植适配 1. 驱动移植 代码路径:longan/kernel/linux-4.9/drivers/usb/serial/option.c diff --git a/drivers/usb/serial/option.c b/drivers/usb/serial/option.c index 9f96dd2..2f25466 100644 --- a/drivers/usb/serial/option.cb/drivers/us…...
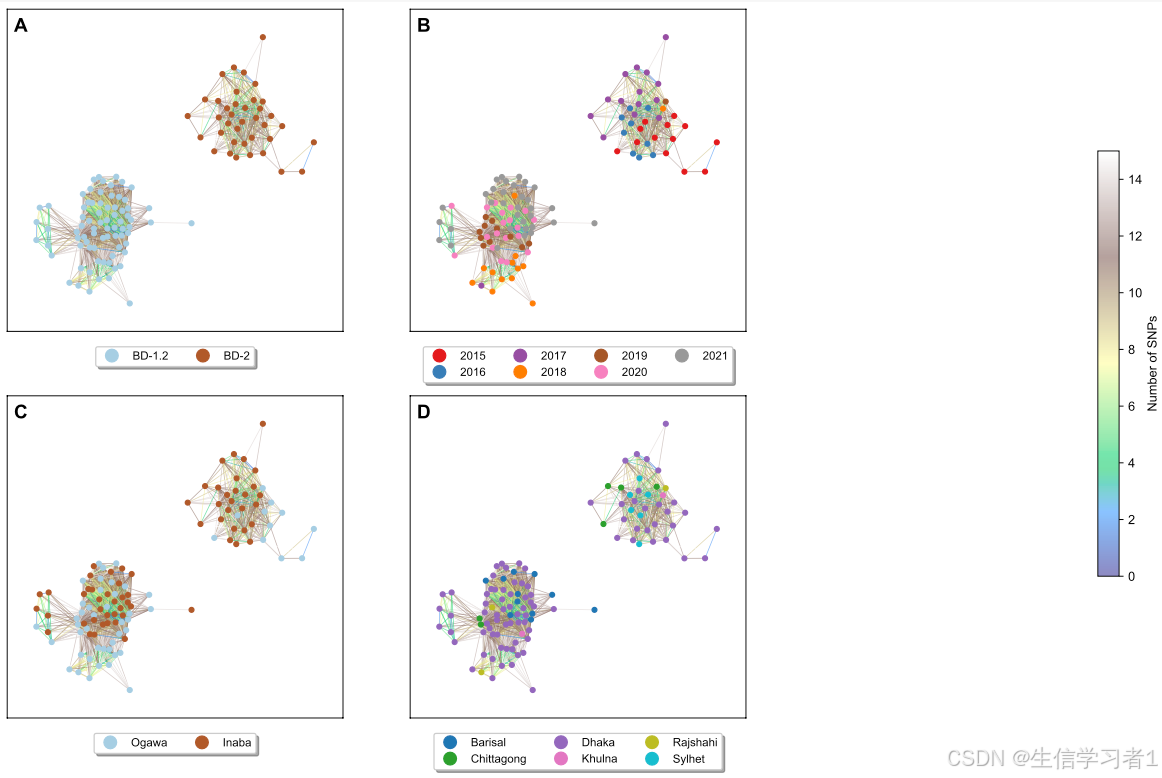
数据分析:Python语言网络图绘制
文章目录 介绍加载R包类别导入数据下载数据画图介绍 网络图是一种图形表示法,用于展示实体之间的关系。在不同的领域中,网络图有着不同的含义和用途:在生物学中,网络图可以用来表示生物分子之间的相互作用,如蛋白质相互作用网络。 加载R包 import pandas as pd import …...

使用ChatGPT引导批判性思维,提升论文的逻辑与说服力的全过程
学境思源,一键生成论文初稿: AcademicIdeas - 学境思源AI论文写作 批判性分析(Critical Analysis) 是论文写作中提升质量和说服力的重要工具。它不仅帮助作者深入理解和评价已有研究,还能指导作者在构建自己论点时更加…...
)
vue限定类型上传文件 最简单实践(单个可文件、可图片)
这个是为了文件导入弄的,内部运维人员使用的 目前还没做删除文件的交互 <el-uploadclass"upload-demo"ref"upload":before-upload"handleBeforeUpload"action"#"accept".xls,.xlsx":limit"1">&l…...

【GUI设计】基于图像分割和边缘算法的GUI系统(7),matlab实现
博主简介: 如需获取设计的完整源代码或者有matlab图像代码项目需求/合作,可联系主页个人简介提供的联系方式或者文末的二维码。 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 本次案例是基于图像分割和边缘算法的GUI系统…...

未来之窗VOS编程工具让你的工作效率翻倍———未来之窗行业应用跨平台架构
未来之窗编程工具概述 平板电脑/手机用于编程具有诸多优点。其便携性强,方便随时随地开展工作。触摸操作直观便捷,长续航能满足长时间需求,启动迅速。支持手写绘图,利于表达想法。能集成多种编程工具,还便于通过云服务…...
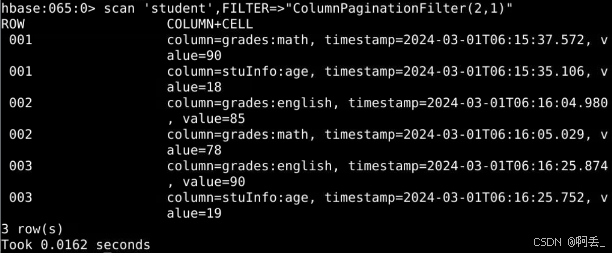
分布式数据库——HBase基本操作
启动HBase: 1.启动hadoop,进入hadoop的sbin中 cd /opt/hadoop/sbin/ 2.初始化namenode hdfs namenode -format 3.启动hdfs ./start-all.sh 4.启动hbase cd /opt/hbase/bin ./start-hbase.sh 5.使用jps查看进程 jps 以下图片则是hbase启动成功~ 运行HBase ./hbase sh…...

Go语言并发编程中的超时与取消机制解析
解锁Python编程的无限可能:《奇妙的Python》带你漫游代码世界 并发编程是Go语言的核心优势之一,而在实际应用中,超时和取消操作会频繁出现。超时机制能够帮助我们理解系统行为,防止系统因为某些任务执行过长而陷入困境。与此同时,取消操作则是应对超时的一种自然反应。此…...

Unity3D UIdocument如何改变层级详解
前言 在Unity3D中,UI文档的层级改变通常涉及UI元素的显示顺序,这是通过UGUI(Unitys Graphical User Interface)系统来实现的。以下是一篇关于如何在Unity3D中改变UI元素层级的详细解析,包括技术详解和代码实现。 对惹…...
Debian与Ubuntu:深入解读两大Linux发行版的历史与联系
Debian与Ubuntu:深入解读两大Linux发行版的历史与联系 引言 在开源操作系统的领域中,Debian和Ubuntu是两款备受瞩目的Linux发行版。它们不仅在技术上有着密切的联系,而且各自的发展历程和理念也对开源社区产生了深远的影响。本文将详细介绍…...

GPU服务器本地搭建Dify+xinference实现大模型应用
文章目录 前言一、显卡驱动配置1.检测显卡2.安装驱动 二、安装nvidia-docker二、安装Xinference1.拉取镜像2.运行Xinference3.模型部署 三、安装Dify1.下载源代码2.启动 Dify3.访问 Dify 四、Dify构建应用1.配置模型供应商2.聊天助手3.Agent 前言 本文使用的GPU服务器为UCloud…...

嵌入式程序设计经验 创建复位函数
在设计嵌入式系统重新时 需要考虑软复位的情况, 软复位时 很多变量都需要重置为初始值, 如果一个个去赋值 很麻烦, 下面是一个简单的办法 主要是对结构体 复位的方法: #include <stdint.h>typedef struct {uint8_t reg1;uint8_t reg2;uint8_t reg3; } StruSimuStat1…...

每天五分钟深度学习框架pytorch:交叉熵计算时的维度是什么?
本文重点 前面我们学习了pytorch中已经封装好的损失函数,已经封装好的损失函数有很多,但是我们并没有详细介绍,原因就是单独介绍损失函数可能难以理解,我们上一章节的目的是让大家先了解一下常见的损失函数,然后再之后的实际使用中遇到哪个损失函数,我们就使用哪个损失函…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...











