Python和VC代码实现希尔伯特变换(Hilbert transform)
文章目录
- 前言
- 一、希尔伯特变换是什么?
- 二、VC中的实现原理及代码示例
- 三、用Python代码实现
- 总结
前言
在数学和信号处理中,**希尔伯特变换(Hilbert transform)**是一个对函数产生定义域相同的函数的线性算子。
希尔伯特变换在信号处理中很重要,能够导出信号u(t)的解析表示。这就意味着将实信号u(t)拓展到复平面,使其满足柯西-黎曼方程。例如,希尔伯特变换引出了傅里叶分析中给定函数的调和共轭,也就是调和分析。等价地说,它是奇异积分算子与傅里叶乘子的一个例子。
希尔伯特变换是以大卫·希尔伯特来命名的,他首先引入了该算子来解决全纯函数的黎曼–希尔伯特问题的一个特殊情况。

一、希尔伯特变换是什么?
希尔伯特变换最初只对周期函数(也就是圆上的函数)有定义,在这种情况下它就是与希尔伯特核的卷积。然而更常见的情况下,对于定义在实直线R(上半平面的边界)上的函数,希尔伯特变换是指与柯西核卷积。希尔伯特变换与帕利-维纳定理有着密切的联系,帕利-维纳定理是将上半平面内的全纯函数与实直线上的函数的傅里叶变换相联系起来的另一种结果。
二、VC中的实现原理及代码示例
VC中可以通过快速傅里叶变换(FFT)来实现希尔伯特变换。
以下是一个简单的C++代码实现希尔伯特变换,需要使用C++11及以上版本的标准库。首先我们需要实现一个FFT函数,然后使用FFT函数来实现希尔伯特变换。
#include <iostream>
#include <cmath>
#include <complex>
#include <vector>using namespace std;typedef complex<double> Complex;
typedef vector<Complex> ComplexVector;// 快速傅里叶变换
void fft(ComplexVector& data) {int n = data.size();if (n <= 1) {return;}// 分离偶数项和奇数项ComplexVector even(n/2), odd(n/2);for (int i = 0; i < n; i += 2) {even[i/2] = data[i];odd[i/2] = data[i+1];}// 递归计算偶数项和奇数项的FFTfft(even);fft(odd);// 计算每个k点的DFTfor (int k = 0; k < n/2; k++) {Complex t = polar(1.0, -2 * M_PI * k / n) * odd[k];data[k] = even[k] + t;data[k+n/2] = even[k] - t;}
}// 希尔伯特变换
void hilbertTransform(ComplexVector& signal) {int n = signal.size();// 扩展信号长度至2的幂次方int n2 = 1;while (n2 < n) {n2 *= 2;}signal.resize(n2);// 进行FFT变换fft(signal);// 对FFT结果进行处理for (int i = 1; i < n; i++) {signal[i] *= 2;}for (int i = n; i < n2; i++) {signal[i] = 0;}signal[0] = 1;signal[n] = 0;// 反向FFT变换fft(signal);for (int i = 0; i < n; i++) {signal[i] = signal[i].imag() / n;}
}int main() {ComplexVector signal = {1, 2, 3, 4, 5, 6, 7, 8};hilbertTransform(signal);// 输出结果for (int i = 0; i < signal.size(); i++) {cout << signal[i] << " ";}cout << endl;return 0;
}
上述代码中,我们首先实现了一个快速傅里叶变换函数fft,然后在hilbertTransform函数中使用FFT计算希尔伯特变换。在希尔伯特变换的计算过程中,我们首先对信号进行了长度的扩展,然后进行了FFT变换,接着根据希尔伯特变换的公式进行了FFT结果的处理,最后进行反向FFT变换得到最终的希尔伯特变换结果。
在上述代码中,我们使用了复数类型complex和向量类型vector来方便地处理信号和FFT结果。在实际应用中,我们可以将输入信号读取自文件或者从实时采集的数据中获取,然后调用hilbertTransform函数进行希尔伯特变换,得到变换后的信号。
三、用Python代码实现
使用Python也可以方便地实现希尔伯特变换。下面是一个使用numpy库实现希尔伯特变换的示例代码:
import numpy as npdef hilbert_transform(signal):"""计算希尔伯特变换"""n = len(signal)# 扩展信号长度至2的幂次方n2 = 1while n2 < n:n2 *= 2signal = np.append(signal, np.zeros(n2 - n))# 进行FFT变换spectrum = np.fft.fft(signal)# 对FFT结果进行处理spectrum[1:n] *= 2spectrum[n:] = 0spectrum[0] = 1spectrum[n] = 0# 反向FFT变换hilbert = np.real(np.fft.ifft(spectrum))hilbert = hilbert[:n]return hilbertif __name__ == "__main__":signal = [1, 2, 3, 4, 5, 6, 7, 8]hilbert = hilbert_transform(signal)# 输出结果print(hilbert)
上述代码中,我们首先将输入信号扩展至2的幂次方长度,然后使用numpy.fft.fft函数进行FFT变换,对FFT结果进行处理,最后使用numpy.fft.ifft函数进行反向FFT变换得到希尔伯特变换结果。
需要注意的是,由于numpy.fft.fft函数返回的结果是按照FFT变换的频率从小到大排列的,而希尔伯特变换则是在时域上进行的,因此我们需要对FFT结果进行一定的处理才能得到正确的希尔伯特变换结果。在上述代码中,我们对FFT结果进行了一系列处理,包括将非零频率部分的幅度乘以2,将非零频率部分之外的频率置零,以及将直流分量和Nyquist频率分量的值分别设为1和0,从而得到正确的希尔伯特变换结果。
总结
在实际应用中,我们可能需要对信号进行预处理和后处理,以得到更好的变换结果。另外,由于FFT算法的复杂度为O(NlogN),在处理大规模的信号时可能会带来一定的计算负担,需要进行优化或者使用更高效的算法。
希望对看到的小伙伴有帮助。
相关文章:

Python和VC代码实现希尔伯特变换(Hilbert transform)
文章目录前言一、希尔伯特变换是什么?二、VC中的实现原理及代码示例三、用Python代码实现总结前言 在数学和信号处理中,**希尔伯特变换(Hilbert transform)**是一个对函数产生定义域相同的函数的线性算子。 希尔伯特变换在信号处…...

嵌入式C语言语法概述
1.gcc概述 GCC全称是GUN C Compiler 随着时代的发展GCC支持的语言越来越多,它的名称变成了GNU Compiler Collection gcc的作用相当于翻译官,把程序设计语言翻译成计算机能理解的机器语言。 (1)gcc -o gcc -o (其…...
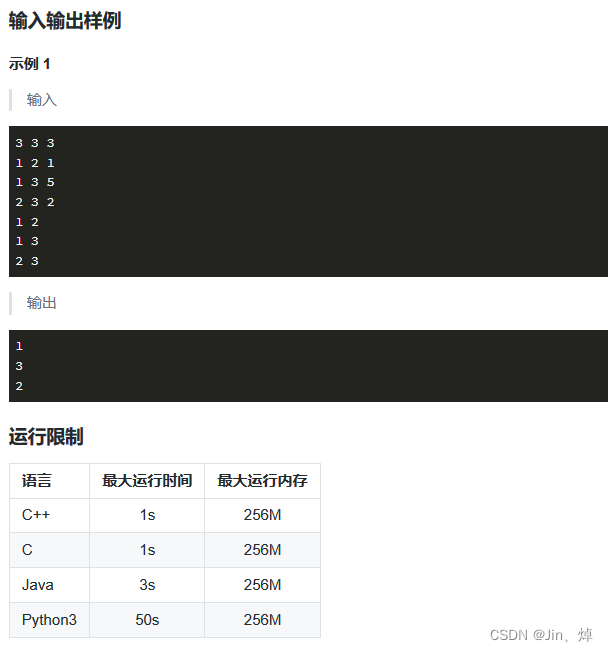
蓝桥杯第19天(Python)(疯狂刷题第3天)
题型: 1.思维题/杂题:数学公式,分析题意,找规律 2.BFS/DFS:广搜(递归实现),深搜(deque实现) 3.简单数论:模,素数(只需要…...
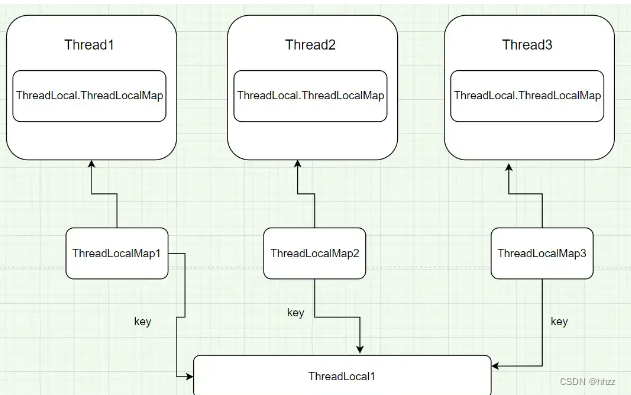
【数据库连接,线程,ThreadLocal三者之间的关系】
一、数据库连接与线程的关系 在实际项目中,数据库连接是很宝贵的资源,以MySQL为例,一台MySQL服务器最大连接数默认是100, 最大可以达到16384。但现实中最多是到200,再多MySQL服务器就承受不住了。因为mysql连接用的是tcp协议&…...
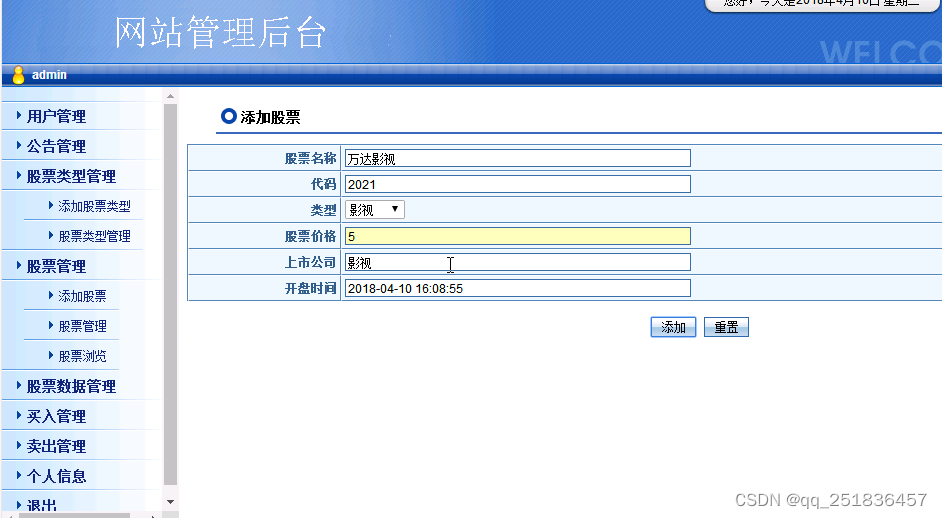
java 虚拟股票交易系统Myeclipse开发mysql数据库web结构jsp编程计算机网页项目
一、源码特点 JSP 虚拟股票交易系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统采用serlvetdaobean,系统具有完整的源代码和数据库,系统主要采用 B/S模式开发。 java 虚拟股票交易系统Myeclips…...

spring如何开启允许循环依赖
如何解决spring循环依赖 在Spring框架中,allowCircularReferences属性是用于控制Bean之间的循环依赖的。循环依赖是指两个或多个Bean之间相互依赖的情况,其中一个Bean依赖于另一个Bean,同时另一个Bean又依赖于第一个Bean。 allowCircularRe…...
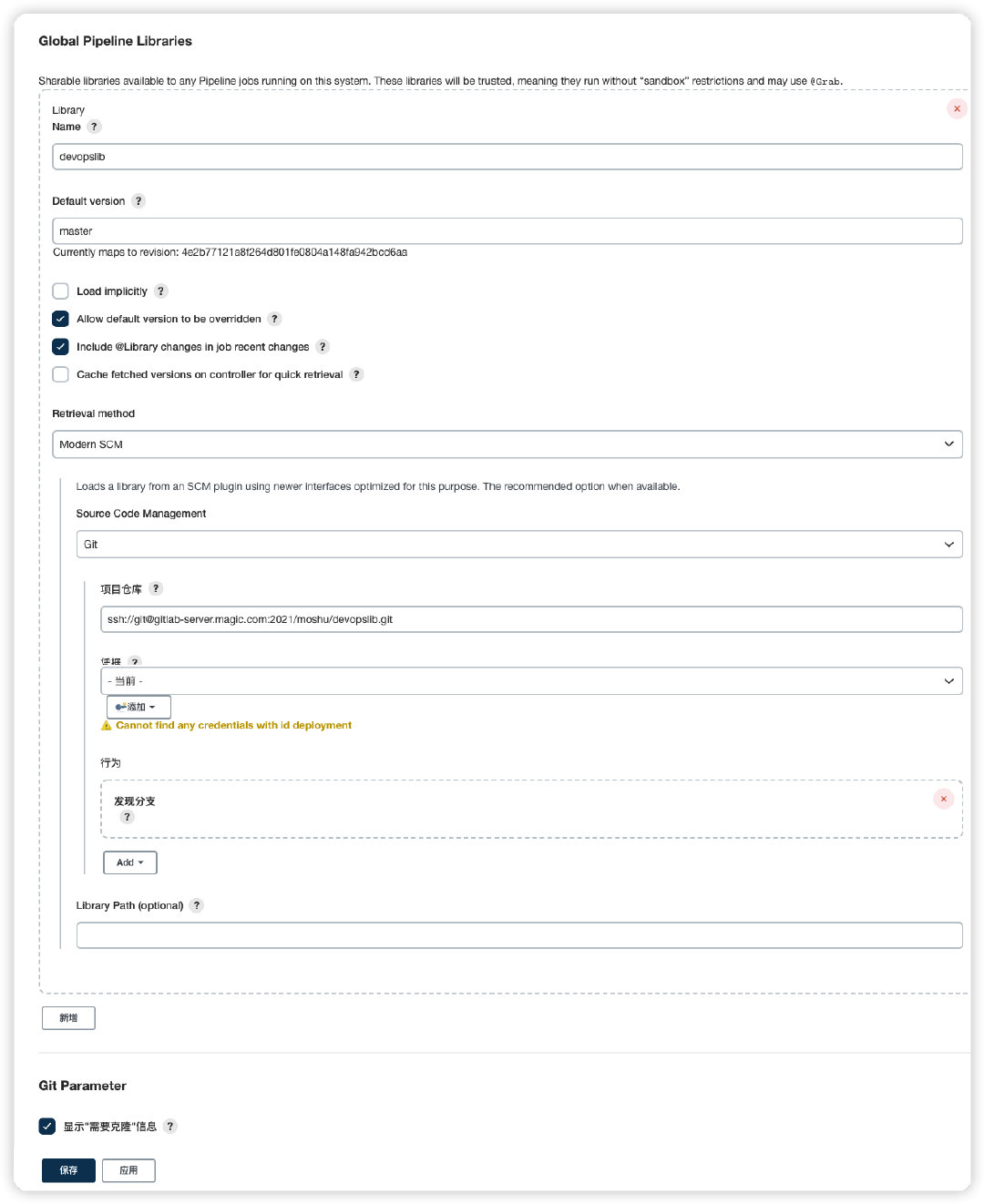
jenkins+sonarqube+自动部署服务
一、jenkins 配置Pipeline 二、新建共享库执行脚本 共享库可以是一个普通的gitlab项目,目录结构如下 三、添加到共享库 Jenkins Dashboard–>系统管理–>系统配置–>Global Pipeline Libraries Name: 共享库名称,自定义即可; Defa…...

【算法系列之动态规划III】背包问题
背包问题 01背包指的是物品只有1个,可以选也可以不选。完全背包是物品有无数个,可以选几个也可以不选。 二维数组01背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次&…...

MONAI-LayerFactory设计与实现
LayerFactory 用于创建图层的工厂对象,这使用给定的工厂函数来实际产生类型或构建可调用程序。这些函数是通过名称来参考的,可以在任何时候添加。 用到的关键技术点: 装饰器(Decorators), 例如:property装饰器,创建…...

Thinkphp 6.0路由的定义
本节课我们来了解一下路由方面的知识,然后简单的使用一下路由的功能。 一.路由简介 1. 路由的作用就是让 URL 地址更加的规范和优雅,或者说更加简洁; 2. 设置路由对 URL 的检测、验证等一系列操作提供了极大的便利性; …...

Kafka系列之:深入理解Kafka集群调优
Kafka系列之:深入理解Kafka集群调优 一、Kafka硬件配置选择二、Kafka内存选择三、CPU选择四、网络选择五、生产者调优六、broker调优七、消费者调优八、Kafka总体调优一、Kafka硬件配置选择 服务器台数选择: 2 * (生产者峰值生产速率 * 副本数 / 100) + 1磁盘选择: Kafka…...

creator-泄漏检测之资源篇
title: creator-泄漏检测之资源篇 categories: Cocos2dx tags: [creator, 优化, 泄漏, 内存] date: 2023-03-29 14:48:48 comments: false mathjax: true toc: true creator-泄漏检测之资源篇 前篇 资源释放 - https://docs.cocos.com/creator/manual/zh/asset/release-manager…...
)
【DevOps】Jenkins 运行任务时遇到 FATAL:Unable to produce a script file 报错(已解决)
文章目录一、问题描述二、定位原因三、解决方案四、其他方案五、总结关键词: Jenkins、Unable to produce a script file、UnmappableCharacterException、IOException: Failed to create a temp file on一、问题描述 由于使用的 Jenkins 存在安全漏洞(…...

Web前端
WEB前端 HTMLCSSJavaScriptjQuery(js框架)Bootstrap(CSS框架)AJAXJSON 文章目录 WEB前端WEB前端三大核心技术Web开发工具文本编辑器集成开发环境(IDE)浏览器选择HTML什么是 HTML?HTML版本变迁HTML-HelloWorldHTML 文档 = 网页HTML 标签属性(Attribute)HTML 常用标签...
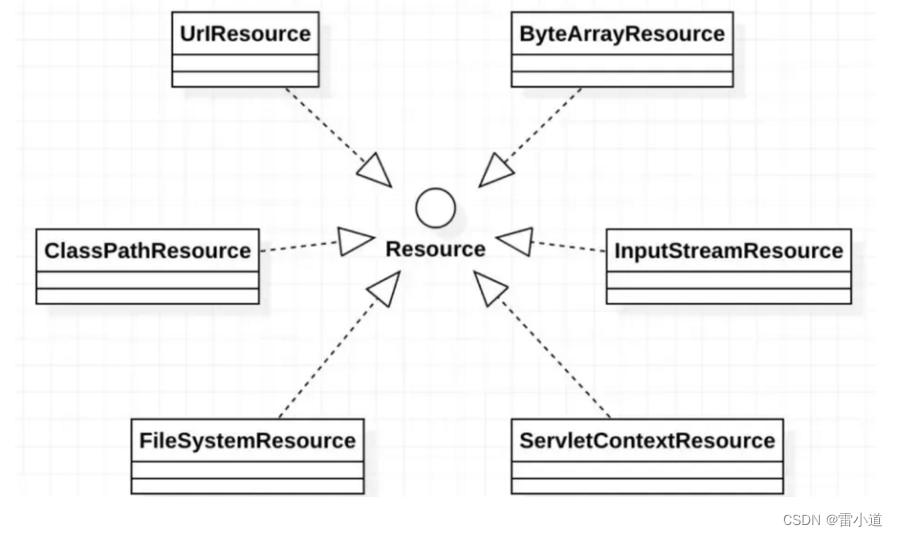
资源操作:Resources
文章目录1. Spring Resources概述1.2 Resource 接口1.3 Resource的实现类1.3.1 UrlResource访问网络资源1.3.2 ClassPathResource访问类路径下资源1.3.3 FileSystemResource访问文件系统资源1.3.4 ServletContextResource1.3.5、InputStreamResource1.3.6、ByteArrayResource1.…...
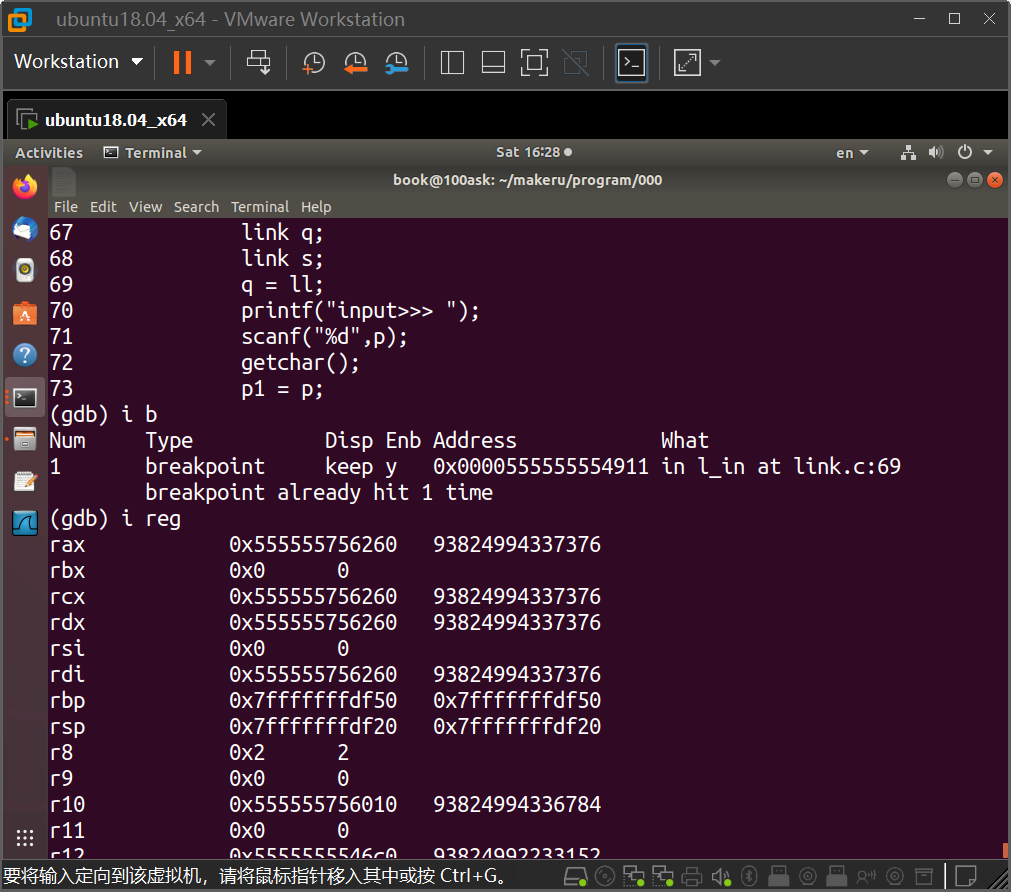
GDB调试的学习
很早就想在好好学一学gdb了,正好最近学算法(以前一直以为干硬件不需要什么特别厉害的算法,结果现在卷起来了。大厂面试题也有复杂一些的算法了) 下面的这些命令是别的博主总结的 GDB 调试过程_gdb调试过程_麷飞花的博客-CSDN博客…...
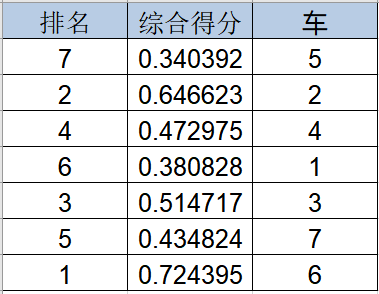
熵值法综合评价分析流程
熵值法综合评价分析流程 一、案例背景 当前有一份数据,是各品牌车各个维度的得分情况,现在想要使用熵值法进行综合评价,得到各品牌车的综合得分,从而进行车型优劣对比,为消费者提供购车依据。 数据如下(数…...

使用Python Pandas库操作Excel表格的技巧
在数据分析和处理中,我们经常需要对Excel表格进行操作。Python Pandas库提供了丰富的API来读取、写入、修改Excel表格。本文将介绍如何使用Python Pandas库操作Excel表格,包括向Excel表格添加新行、创建Excel表格等。 1.向Excel表格添加新行 下面是一个…...
LeetCode练习七:动态规划上:线性动态规划
文章目录一、 动态规划基础知识1.1 动态规划简介1.2 动态规划的特征1.2.1 最优子结构性质1.2.2 重叠子问题性质1.2.3 无后效性1.3 动态规划的基本思路1.4 动态规划基础应用1.4.1 斐波那契数1.4.2 爬楼梯1.4.3 不同路径1.5 个人总结二、记忆化搜索2.1 记忆化搜索简介2.2 记忆化搜…...

基于正点原子F407开发版和SPI接口屏移植touchgfx完整教程(一)
一、相关软件包安装 1、打开cubemx包管理器 2、安装F4软件包 3、安装touchgfx软件包 二、工程配置 1、新建工程 2、sys配置 3、rcc配置 4、crc配置 5、添加touchgfx软件包 6、配置touchgfx软件包 将width和height改为自己屏幕尺寸 7、生成工程 三、代码修改 1、将屏幕相关驱…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
