【理论推导】变分自动编码器 Variational AutoEncoder(VAE)
变分推断 (Variational Inference)
变分推断属于对隐变量模型 (Latent Variable Model) 处理的一种技巧,其概率图如下所示

我们将 X={x1,...xN}X=\{ x_1,...x_N \}X={x1,...xN} 看作是每个样本可观测的一组数据,而将对应的 Z={z1,...,zN}Z=\{z_1,...,z_N\}Z={z1,...,zN} 看作是该组数据对应的高维空间下的对应样本点,例如使用 XXX 表示一个班同学的所有成绩,而将 ZZZ 看作是同学的学习能力。对于更复杂的一些情况,例如图像生成任务,使用 XXX 表示数据集中的每张图像,而使用 ZZZ 表示更高维的信息,例如基于类别/语义等控制信息。
对于生成任务,我们经常希望利用观测数据 XXX 建模随机变量 xxx 的真实分布 p(x)p(x)p(x),使用 zzz 来辅助概率推导,那么核心点在于计算两个条件概率分布 p(x∣z)p(x|z)p(x∣z) 与 p(z∣x)p(z|x)p(z∣x),通常可以使用一些先验知识假定 p(x∣z)p(x|z)p(x∣z) 服从某种概率分布(例如对于学习能力为 ggg 的同学成绩假定服从在 ggg 附近的高斯分布),但对于 p(z∣x)p(z|x)p(z∣x),注意到
p(z∣x)=p(z)p(x∣z)p(x)p(z|x) = \frac{p(z)p(x|z)}{p(x)} p(z∣x)=p(x)p(z)p(x∣z)
zzz 是辅助建模的变量,可以假定其服从某已知的分布,但对于归一化项 p(x)p(x)p(x),有
p(x)=∫zp(x,z)dz=∫zp(z)p(x∣z)dzp(x) = \int_z p(x,z)dz = \int_z p(z) p(x|z) dz p(x)=∫zp(x,z)dz=∫zp(z)p(x∣z)dz
由于 zzz 是一个非常高维的信息,p(x)p(x)p(x) 是很难直接计算积分进行处理的,所以 p(z∣x)p(z|x)p(z∣x) 也是很难处理的,我们通常使用优化的方法来拟合出概率分布 p(z∣x)p(z|x)p(z∣x)
首先,我们考虑随机变量 zzz 与 xxx 之间的关系,假定 p(x)p(x)p(x) 表示真实的数据分布,即我们观测到的数据 x∼p(x)x\sim p(x)x∼p(x),q(z∣x)q(z|x)q(z∣x) 为任一条件概率分布(通常是使用模型拟合出来的分布),有
logp(x)=logp(x,z)−logp(z∣x)=logp(x,z)q(z∣x)−logp(z∣x)q(z∣x)\begin{align} \log p(x) &= \log p(x,z) - \log p(z|x) \nonumber \\&=\log\frac{p(x,z)}{q(z|x)} - \log\frac{p(z|x)}{q(z|x)} \nonumber \end{align} logp(x)=logp(x,z)−logp(z∣x)=logq(z∣x)p(x,z)−logq(z∣x)p(z∣x)
对左右两式计算关于隐变量 zzz 的期望,有
left=Ez∼q(z∣x)[logp(x)]=logp(x)∫zq(z∣x)dz=logp(x)right=Ez∼q(z∣x)[logp(x,z)q(z∣x)−logp(z∣x)q(z∣x)]=∫zq(z∣x)logp(x,z)q(z∣x)dz+∫zq(z∣x)logq(z∣x)p(z∣x)dz=∫zq(z∣x)logp(x,z)q(z∣x)dz+KL(q(z∣x)∣∣p(z∣x))\begin{align} \text{left} &= \mathbb E_{z\sim q(z|x)}[\log p(x)] = \log p(x) \int_z q(z|x) dz = \log p(x) \nonumber \\\text{right} &= \mathbb E_{z\sim q(z|x)}[\log\frac{p(x,z)}{q(z|x)} - \log\frac{p(z|x)}{q(z|x)}] = \int_z q(z|x) \log\frac{p(x,z)}{q(z|x)} dz + \int_z q(z|x) \log\frac{q(z|x)}{p(z|x)} dz \nonumber \\ &= \int_z q(z|x) \log\frac{p(x,z)}{q(z|x)} dz + \text{KL}(q(z|x)||p(z|x)) \nonumber \end{align} leftright=Ez∼q(z∣x)[logp(x)]=logp(x)∫zq(z∣x)dz=logp(x)=Ez∼q(z∣x)[logq(z∣x)p(x,z)−logq(z∣x)p(z∣x)]=∫zq(z∣x)logq(z∣x)p(x,z)dz+∫zq(z∣x)logp(z∣x)q(z∣x)dz=∫zq(z∣x)logq(z∣x)p(x,z)dz+KL(q(z∣x)∣∣p(z∣x))
其中 ∫zq(z∣x)logp(x,z)q(z∣x)dz\int_z q(z|x) \log\frac{p(x,z)}{q(z|x)} dz∫zq(z∣x)logq(z∣x)p(x,z)dz 被称作是信心下界 (Evidence Lower Bound),简单记作 ELBO,名字来源是由于KL散度满足恒大于等于0的性质,因此有 logp(x)≥ELBO\log p(x)\geq \text{ELBO}logp(x)≥ELBO,当 q(z∣x)=p(z∣x)q(z|x) = p(z|x)q(z∣x)=p(z∣x) 时取等,因此我们有如下公式
logp(x)=ELBO+KL(q(z∣x)∣∣p(z∣x))≥ELBO\begin{align} \log p(x) = \text{ELBO}+\text{KL}(q(z|x)||p(z|x)) \geq \text{ELBO} \end{align} logp(x)=ELBO+KL(q(z∣x)∣∣p(z∣x))≥ELBO
如果我们希望 q(z∣x)q(z|x)q(z∣x) 逼近真实条件概率分布 p(z∣x)p(z|x)p(z∣x),在观测数据 xxx 给定的情况下,最小化KL散度等价于最大化ELBO
假定 q(z∣x)q(z|x)q(z∣x) 表示的概率分布由参数 ϕ\phiϕ 决定(例如使用神经网络表示 qϕq_\phiqϕ,我们一般不改变网络结构,而只针对参数进行优化),那么该拟合问题的优化目标如下所示
ϕ^=argmaxϕELBO\hat{\phi} = \arg\max_\phi \text{ELBO} ϕ^=argϕmaxELBO
如果我们采用随机梯度下降法来进行优化 (Stochastic Gradient Varational Inference),首先要计算 ϕ\phiϕ 的导数
▽ϕELBO=▽ϕ∫zqϕ(z∣x)logp(x,z)qϕ(z∣x)dz=∫z▽ϕqϕ(z∣x)logp(x,z)qϕ(z∣x)dz+∫zqϕ(z∣x)▽ϕlogp(x,z)qϕ(z∣x)dz\begin{align} \triangledown_\phi \text{ELBO} &= \triangledown_\phi \int_z q_\phi(z|x) \log\frac{p(x,z)}{q_\phi(z|x)} dz \nonumber \\ &= \int_z \triangledown_\phi q_\phi(z|x) \log\frac{p(x,z)}{q_\phi(z|x)} dz + \int_z q_\phi(z|x) \triangledown_\phi \log\frac{p(x,z)}{q_\phi(z|x)} dz \nonumber \end{align} ▽ϕELBO=▽ϕ∫zqϕ(z∣x)logqϕ(z∣x)p(x,z)dz=∫z▽ϕqϕ(z∣x)logqϕ(z∣x)p(x,z)dz+∫zqϕ(z∣x)▽ϕlogqϕ(z∣x)p(x,z)dz
注意到,对于第二项,有
∫zqϕ(z∣x)▽ϕlogp(x,z)qϕ(z∣x)dz=−∫zqϕ(z∣x)▽ϕlogqϕ(z∣x)dz=−∫z▽ϕqϕ(z∣x)dz=−▽ϕ∫zqϕ(z∣x)dz=0\int_z q_\phi(z|x) \triangledown_\phi \log\frac{p(x,z)}{q_\phi(z|x)} dz = - \int_z q_\phi(z|x) \triangledown_\phi \log q_\phi(z|x) dz = - \int_z \triangledown_\phi q_\phi(z|x) dz = - \triangledown_\phi \int_z q_\phi(z|x) dz = 0 ∫zqϕ(z∣x)▽ϕlogqϕ(z∣x)p(x,z)dz=−∫zqϕ(z∣x)▽ϕlogqϕ(z∣x)dz=−∫z▽ϕqϕ(z∣x)dz=−▽ϕ∫zqϕ(z∣x)dz=0
因此,有如下等式
▽ϕELBO=∫zqϕ(z∣x)▽ϕlogqϕ(z∣x)logp(x,z)qϕ(z∣x)dz=Ez∼qϕ(z∣x)[▽ϕlogqϕ(z∣x)logp(x,z)qϕ(z∣x)]\begin{align} \triangledown_\phi \text{ELBO} &= \int_z q_\phi(z|x) \triangledown_\phi \log q_\phi(z|x) \log\frac{p(x,z)}{q_\phi(z|x)} dz \nonumber \\ &= \mathbb E_{z\sim q_\phi(z|x)}[\triangledown_\phi \log q_\phi(z|x) \log\frac{p(x,z)}{q_\phi(z|x)}] \end{align} \nonumber ▽ϕELBO=∫zqϕ(z∣x)▽ϕlogqϕ(z∣x)logqϕ(z∣x)p(x,z)dz=Ez∼qϕ(z∣x)[▽ϕlogqϕ(z∣x)logqϕ(z∣x)p(x,z)]
使用 Monto-Carlo 采样方法计算期望,即 zi∼qϕ(z∣x)(i=1...L)z_i \sim q_\phi(z|x) \;\;(i=1...L)zi∼qϕ(z∣x)(i=1...L)
▽ϕELBO≈1L∑i=1L▽ϕlogqϕ(zi∣x)logp(x,zi)qϕ(zi∣x)\triangledown_\phi \text{ELBO} \approx \frac{1}{L} \sum_{i=1}^L \triangledown_\phi \log q_\phi(z_i|x) \log\frac{p(x,z_i)}{q_\phi(z_i|x)} ▽ϕELBO≈L1i=1∑L▽ϕlogqϕ(zi∣x)logqϕ(zi∣x)p(x,zi)
注意到,式子中包含 ▽ϕlogqϕ(zi∣x)\triangledown_\phi \log q_\phi(z_i|x)▽ϕlogqϕ(zi∣x),以下为 y=log(x)y=\log(x)y=log(x) 的函数图像

在 xxx 较小时值的变化范围很大,因此直观上来看 ▽ϕlogqϕ(zi∣x)logp(x,zi)qϕ(zi∣x)\triangledown_\phi \log q_\phi(z_i|x) \log\frac{p(x,z_i)}{q_\phi(z_i|x)}▽ϕlogqϕ(zi∣x)logqϕ(zi∣x)p(x,zi) 方差较大,对于每个 xxx 都需要大量采样 zzz 才能得到一个较为准确的期望值,实际应用时存在较大困难,因此引入如下重参数化技巧 (Re-parameterization)
重参数化技巧:我们希望解耦随机变量 zzz 中的随机性与 ϕ\phiϕ 之间的关系,使得计算期望时随机变量服从的概率分布 z∼qϕ(z∣x)z\sim q_\phi(z|x)z∼qϕ(z∣x) 转变为某个已知的概率分布,我们假定存在某随机变量 ϵ∼pϵ(ϵ)\epsilon \sim p_\epsilon(\epsilon)ϵ∼pϵ(ϵ),满足 z=gϕ(ϵ,x)z = g_\phi(\epsilon, x)z=gϕ(ϵ,x),我们有 ∣qϕ(z∣x)dz∣=∣pϵ(ϵ)dϵ∣\left | q_{\phi }(z|x)dz \right |=\left | p_\epsilon(\epsilon )d\epsilon \right |∣qϕ(z∣x)dz∣=∣pϵ(ϵ)dϵ∣,因此,有下式
▽ϕELBO=▽ϕ∫zqϕ(z∣x)logp(x,z)qϕ(z∣x)dz=▽ϕ∫zlogp(x,z)qϕ(z∣x)pϵ(ϵ)dϵ=∫z▽ϕlogp(x,z)qϕ(z∣x)pϵ(ϵ)dϵ=Eϵ∼pϵ[▽ϕlogp(x,z)qϕ(z∣x)]=Eϵ∼pϵ[▽zlogp(x,z)qϕ(z∣x)▽ϕgϕ(ϵ,x)]\begin{align} \triangledown_\phi \text{ELBO} &= \triangledown_\phi \int_z q_\phi(z|x) \log\frac{p(x,z)}{q_\phi(z|x)} dz \nonumber \\ &= \triangledown_\phi \int_z \log\frac{p(x,z)}{q_\phi(z|x)} p_\epsilon(\epsilon) d\epsilon \nonumber \\ &= \int_z \triangledown_\phi \log\frac{p(x,z)}{q_\phi(z|x)} p_\epsilon(\epsilon) d\epsilon \nonumber \\ &= \mathbb E_{\epsilon\sim p_\epsilon}[ \triangledown_\phi\log\frac{p(x,z)}{q_\phi(z|x)}] \nonumber \\ &= \mathbb E_{\epsilon\sim p_\epsilon}[ \triangledown_z\log\frac{p(x,z)}{q_\phi(z|x)} \triangledown_\phi g_\phi(\epsilon,x)] \nonumber \end{align} ▽ϕELBO=▽ϕ∫zqϕ(z∣x)logqϕ(z∣x)p(x,z)dz=▽ϕ∫zlogqϕ(z∣x)p(x,z)pϵ(ϵ)dϵ=∫z▽ϕlogqϕ(z∣x)p(x,z)pϵ(ϵ)dϵ=Eϵ∼pϵ[▽ϕlogqϕ(z∣x)p(x,z)]=Eϵ∼pϵ[▽zlogqϕ(z∣x)p(x,z)▽ϕgϕ(ϵ,x)]
变分自动编码器 (Variational AutoEncoder)
变分自编码器是变分推断与自编码器的一种组合,首先来简单介绍一下自编码器,经验可知,对于图像 x∈RH×W×3x\in \R^{H\times W\times 3}x∈RH×W×3 等真实数据的高维数据,它们通常在空间中是稀疏分布的,大致分布在高维空间的某个流形上面,因此,我们希望将其投影到某个稠密分布的空间上,使其满足某些性质(例如,在该稠密空间上采样的任一一个点,投影回原始图像空间都能得到一个接近真实的图像),我们使用神经网络来执行不同表示空间的转换操作,如下所示

AE主要有encoder和decoder两个部分组成,其中encoder和decoder都是神经网络。其中encoder负责将高维输入转换为低维的隐变量,decoder负责将低维的隐变量转换为高维的图像输出,其中输出要跟输入尽可能的相似
通常情况下,网络的拟合能力要强于训练数据的多样性,假如 Autoencoders 中的 encoder 和 decoder 都具有无限的拟合能力,那么理论上我们就可以无损地把任何高维数据都压缩至维度为 1,无损的数据压缩往往会使得隐空间缺乏可解释性。在大多数情况下,空间转化不仅仅是为了降低数据维度,而是在降低数据维度的同时还能在隐空间中保留数据的主要结构信息。我们目前的损失函数只对每个样本点处进行约束,而并没有整个隐空间上给出约束信息,这使得该网络不能在样本点与样本点之间得到较好的插值结果

上图所示三种颜色表示三个样本点在隐空间上的位置,如果不引入额外的约束,只在样本点的某个小邻域内可以得到合理的图像结果,但大部分位置 Decoder 不能给出一个合理的图像生成结果。我们希望,对隐空间的样本点施加一个噪声的情况下,依旧约束 Decoder 重建出一张与原始图像相似的图片,整体流程如下所示

注意到对于上述流程中,采样这一步是无法进行反向传播的,采用重参数化技巧解耦 zzz 的随机性和与参数 ϕ\phiϕ 之间的关系。通常假定 z∣x∼N(μ(x),σ2(x)I)z|x \sim \mathcal N (\mu(x), \sigma^2(x)I)z∣x∼N(μ(x),σ2(x)I),那么有
z=μ(x)+σ(x)ϵz = \mu(x) + \sigma(x) \epsilon z=μ(x)+σ(x)ϵ
其中 ϵ∼N(0,I)\epsilon \sim \mathcal{N}(0,I)ϵ∼N(0,I),网络结构如下所示
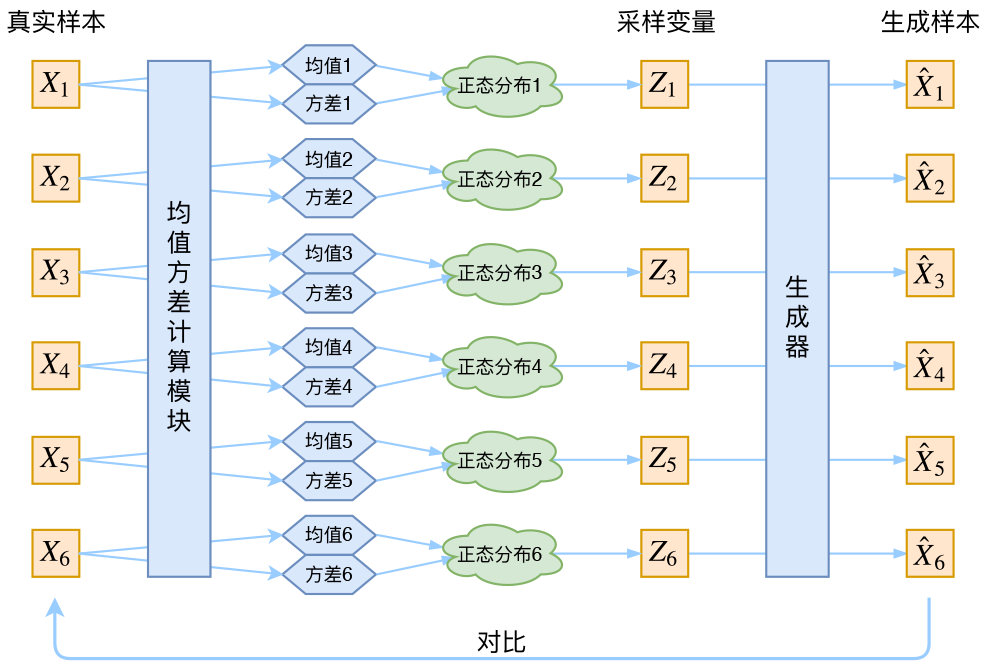
对于以上网络结构,显然噪声会增加重构的难度,其中噪声强度(方差)通过一个神经网络算出来的,如果不施加额外的约束,网络会倾向于让方差为0,模型会慢慢退化成普通的AutoEncoder,噪声不再起作用。
因此,为了避免模型退化,同时保证有意义的 p(z)p(z)p(z) 分布(方便图像的生成任务),VAE让所有的 p(z∣x)p(z|x)p(z∣x) 向标准正态分布看齐,如果所有的 p(z∣x)p(z|x)p(z∣x) 都很接近标准正态分布 N(0,1)\mathcal{N}(0,1)N(0,1),那么有
p(z)=∫xp(z∣x)p(x)dx=∫xN(0,1)p(x)dx=N(0,1)p(z) = \int_x p(z|x) p(x) dx = \int_x \mathcal{N}(0,1) p(x) dx = \mathcal{N}(0,1) p(z)=∫xp(z∣x)p(x)dx=∫xN(0,1)p(x)dx=N(0,1)
然后我们就可以从 N(0,1)\mathcal{N}(0,1)N(0,1) 中采样来生成图像
约束项由 KL 散度给出,有如下结论:对于一维高斯分布 p∼N(μ1,σ12)p~\sim \mathcal{N}(\mu_1,\sigma_1^2)p ∼N(μ1,σ12) 和 q∼N(μ2,σ22)q~\sim \mathcal{N}(\mu_2,\sigma_2^2)q ∼N(μ2,σ22),满足
KL(p∣∣q)=logσ2σ1+σ12+(μ1−μ2)22σ22−12\text{KL}(p||q) = \log\frac{\sigma_2}{\sigma_1} + \frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2} - \frac{1}{2} KL(p∣∣q)=logσ1σ2+2σ22σ12+(μ1−μ2)2−21
具体细节可见 高斯分布的KL散度,进一步,假定隐变量各维度是相互独立的,可以给出如下损失函数约束项(对于第 i 个分量)
KL(N(μ(i)(x),σ(i)(x)),N(0,1))=12(μ(i)(x)2+σ(i)(x)2−2logσ(i)(x)−1)\text{KL}(\mathcal{N}(\mu^{(i)}(x),\sigma^{(i)}(x)), \mathcal{N}(0,1)) = \frac{1}{2}(\mu^{(i)}(x)^2+\sigma^{(i)}(x)^2−2\log\sigma^{(i)}(x)−1) KL(N(μ(i)(x),σ(i)(x)),N(0,1))=21(μ(i)(x)2+σ(i)(x)2−2logσ(i)(x)−1)
从数学角度来说,该优化问题可表示为
θ^,ϕ^=argminθ,ϕKL(qϕ(z∣x)∣∣pθ(z∣x))=argmaxθ,ϕELBO=argmaxθ,ϕEz∼qϕ(z∣x)[logpθ(x∣z)]−KL(qϕ(z∣x)∣∣pθ(z∣x))\begin{align} \hat{\theta}, \hat{\phi} &= \arg \min_{\theta,\phi} \text{KL}(q_\phi(z|x)||p_\theta(z|x)) \\&= \arg \max_{\theta,\phi} \text{ELBO} \\&= \arg \max_{\theta,\phi} \mathbb{E}_{z\sim q_\phi(z|x)} [\log p_\theta(x|z)] - \text{KL}(q_\phi(z|x)||p_\theta(z|x)) \end{align} θ^,ϕ^=argθ,ϕminKL(qϕ(z∣x)∣∣pθ(z∣x))=argθ,ϕmaxELBO=argθ,ϕmaxEz∼qϕ(z∣x)[logpθ(x∣z)]−KL(qϕ(z∣x)∣∣pθ(z∣x))
参考资料
白板推导机器学习
相关文章:

【理论推导】变分自动编码器 Variational AutoEncoder(VAE)
变分推断 (Variational Inference) 变分推断属于对隐变量模型 (Latent Variable Model) 处理的一种技巧,其概率图如下所示 我们将 X{x1,...xN}X\{ x_1,...x_N \}X{x1,...xN} 看作是每个样本可观测的一组数据,而将对应的 Z{z1,...,zN}Z\{z_1,...,z_N…...

【哈希表:哈希函数构造方法、哈希冲突的处理】
预测未来的最好方法就是创造它💦 目录 一、什么是Hash表 二、Hash冲突 三、Hash函数的构造方法 1. 直接定址法 2. 除余法 3. 基数转换法 4. 平方取中法 5. 折叠法 6. 移位法 7. 随机数法 四、处理冲突方法 1. 开放地址法 • 线性探测法 …...

HTML5 应用程序缓存
HTML5 应用程序缓存 使用 HTML5,通过创建 cache manifest 文件,可以轻松地创建 web 应用的离线版本。这意味着,你可以在没有网络连接的情况下进行访问。 什么是应用程序缓存(Application Cache)? HTML5 引…...

全国计算机等级考试三级网络技术选择题考点
目录 第一章 网络系统结构与设计的基本原则 第二章 中小型网络系统总体规划与设计方法 第三章 IP地址规划技术 第四章 路由设计基础 第五章 局域网技术基础应用 第六/七章 交换机/路由器及其配置 第八章 无线局域网技术 第九章 计算机网络信息服务系统的安装与…...

Python和VC代码实现希尔伯特变换(Hilbert transform)
文章目录前言一、希尔伯特变换是什么?二、VC中的实现原理及代码示例三、用Python代码实现总结前言 在数学和信号处理中,**希尔伯特变换(Hilbert transform)**是一个对函数产生定义域相同的函数的线性算子。 希尔伯特变换在信号处…...

嵌入式C语言语法概述
1.gcc概述 GCC全称是GUN C Compiler 随着时代的发展GCC支持的语言越来越多,它的名称变成了GNU Compiler Collection gcc的作用相当于翻译官,把程序设计语言翻译成计算机能理解的机器语言。 (1)gcc -o gcc -o (其…...
蓝桥杯第19天(Python)(疯狂刷题第3天)
题型: 1.思维题/杂题:数学公式,分析题意,找规律 2.BFS/DFS:广搜(递归实现),深搜(deque实现) 3.简单数论:模,素数(只需要…...
【数据库连接,线程,ThreadLocal三者之间的关系】
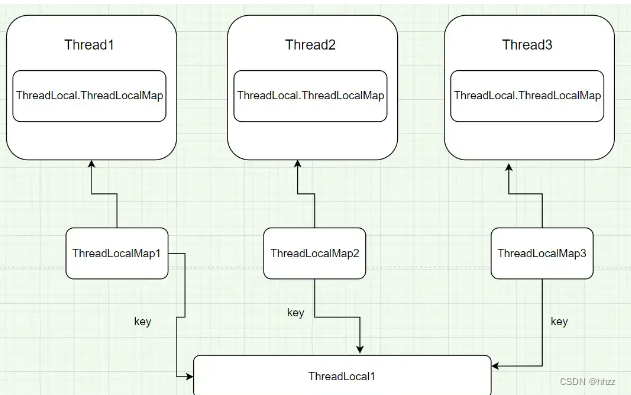
一、数据库连接与线程的关系 在实际项目中,数据库连接是很宝贵的资源,以MySQL为例,一台MySQL服务器最大连接数默认是100, 最大可以达到16384。但现实中最多是到200,再多MySQL服务器就承受不住了。因为mysql连接用的是tcp协议&…...
java 虚拟股票交易系统Myeclipse开发mysql数据库web结构jsp编程计算机网页项目
一、源码特点 JSP 虚拟股票交易系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统采用serlvetdaobean,系统具有完整的源代码和数据库,系统主要采用 B/S模式开发。 java 虚拟股票交易系统Myeclips…...

spring如何开启允许循环依赖
如何解决spring循环依赖 在Spring框架中,allowCircularReferences属性是用于控制Bean之间的循环依赖的。循环依赖是指两个或多个Bean之间相互依赖的情况,其中一个Bean依赖于另一个Bean,同时另一个Bean又依赖于第一个Bean。 allowCircularRe…...
jenkins+sonarqube+自动部署服务
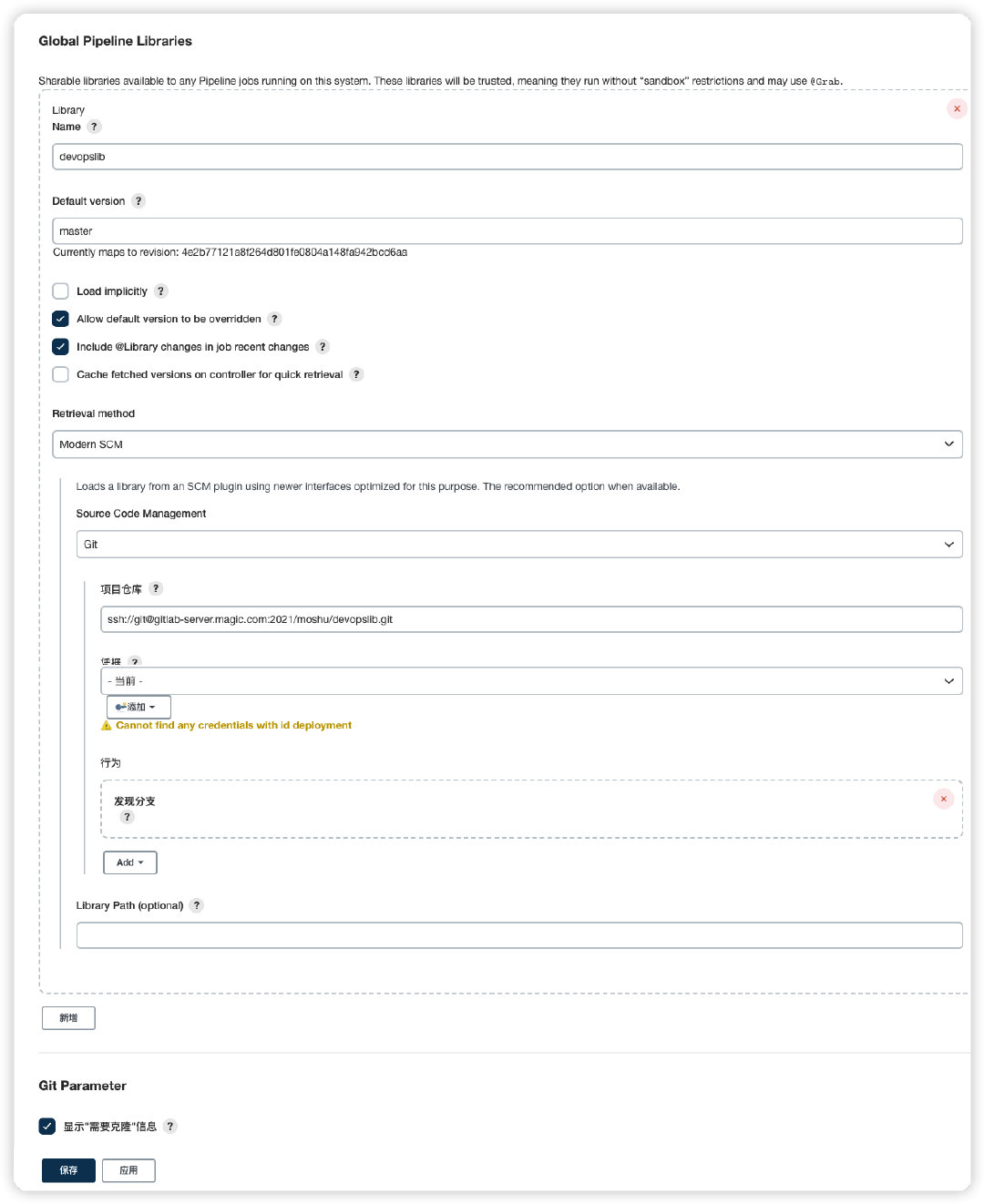
一、jenkins 配置Pipeline 二、新建共享库执行脚本 共享库可以是一个普通的gitlab项目,目录结构如下 三、添加到共享库 Jenkins Dashboard–>系统管理–>系统配置–>Global Pipeline Libraries Name: 共享库名称,自定义即可; Defa…...

【算法系列之动态规划III】背包问题
背包问题 01背包指的是物品只有1个,可以选也可以不选。完全背包是物品有无数个,可以选几个也可以不选。 二维数组01背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次&…...

MONAI-LayerFactory设计与实现
LayerFactory 用于创建图层的工厂对象,这使用给定的工厂函数来实际产生类型或构建可调用程序。这些函数是通过名称来参考的,可以在任何时候添加。 用到的关键技术点: 装饰器(Decorators), 例如:property装饰器,创建…...

Thinkphp 6.0路由的定义
本节课我们来了解一下路由方面的知识,然后简单的使用一下路由的功能。 一.路由简介 1. 路由的作用就是让 URL 地址更加的规范和优雅,或者说更加简洁; 2. 设置路由对 URL 的检测、验证等一系列操作提供了极大的便利性; …...

Kafka系列之:深入理解Kafka集群调优
Kafka系列之:深入理解Kafka集群调优 一、Kafka硬件配置选择二、Kafka内存选择三、CPU选择四、网络选择五、生产者调优六、broker调优七、消费者调优八、Kafka总体调优一、Kafka硬件配置选择 服务器台数选择: 2 * (生产者峰值生产速率 * 副本数 / 100) + 1磁盘选择: Kafka…...

creator-泄漏检测之资源篇
title: creator-泄漏检测之资源篇 categories: Cocos2dx tags: [creator, 优化, 泄漏, 内存] date: 2023-03-29 14:48:48 comments: false mathjax: true toc: true creator-泄漏检测之资源篇 前篇 资源释放 - https://docs.cocos.com/creator/manual/zh/asset/release-manager…...
)
【DevOps】Jenkins 运行任务时遇到 FATAL:Unable to produce a script file 报错(已解决)
文章目录一、问题描述二、定位原因三、解决方案四、其他方案五、总结关键词: Jenkins、Unable to produce a script file、UnmappableCharacterException、IOException: Failed to create a temp file on一、问题描述 由于使用的 Jenkins 存在安全漏洞(…...

Web前端
WEB前端 HTMLCSSJavaScriptjQuery(js框架)Bootstrap(CSS框架)AJAXJSON 文章目录 WEB前端WEB前端三大核心技术Web开发工具文本编辑器集成开发环境(IDE)浏览器选择HTML什么是 HTML?HTML版本变迁HTML-HelloWorldHTML 文档 = 网页HTML 标签属性(Attribute)HTML 常用标签...
资源操作:Resources
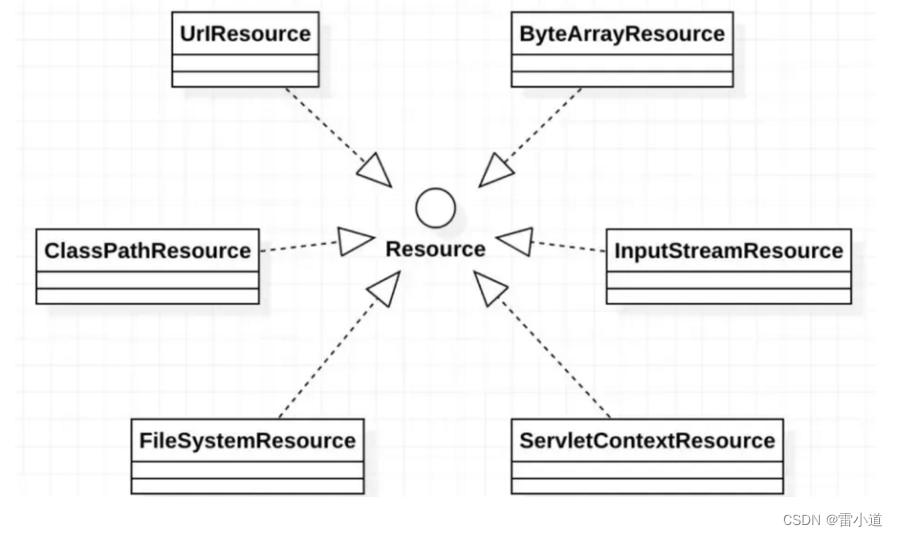
文章目录1. Spring Resources概述1.2 Resource 接口1.3 Resource的实现类1.3.1 UrlResource访问网络资源1.3.2 ClassPathResource访问类路径下资源1.3.3 FileSystemResource访问文件系统资源1.3.4 ServletContextResource1.3.5、InputStreamResource1.3.6、ByteArrayResource1.…...
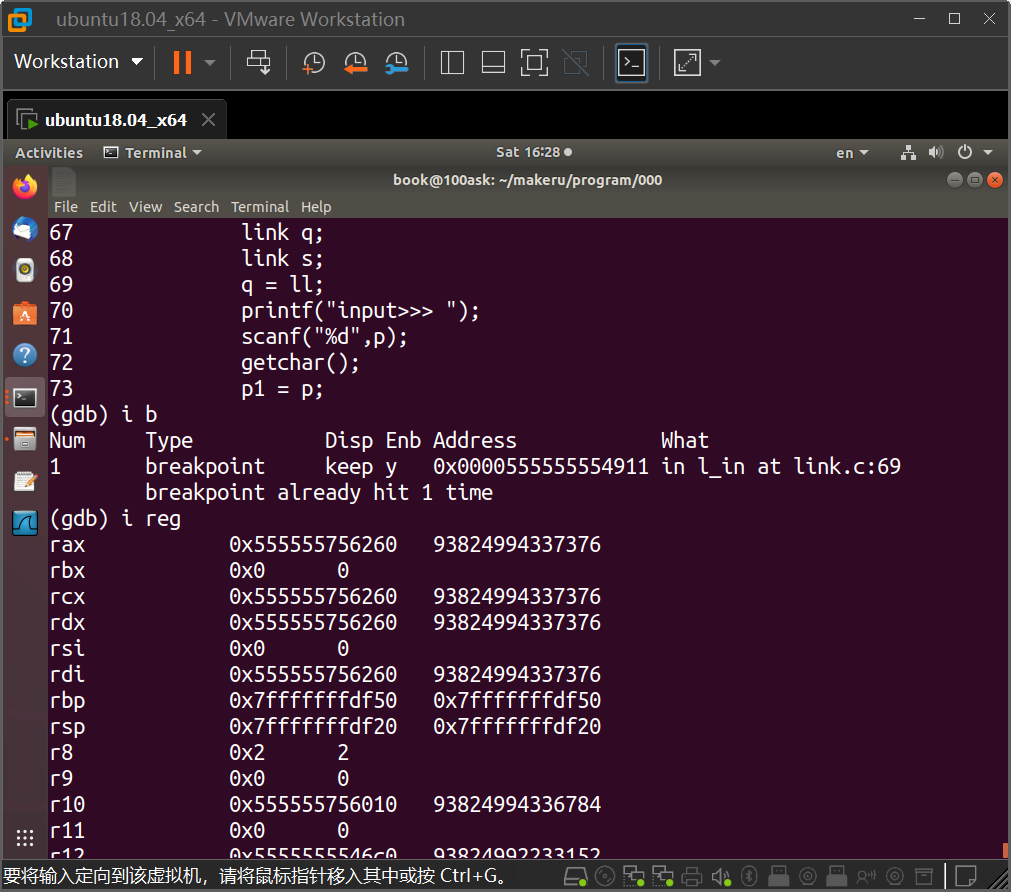
GDB调试的学习
很早就想在好好学一学gdb了,正好最近学算法(以前一直以为干硬件不需要什么特别厉害的算法,结果现在卷起来了。大厂面试题也有复杂一些的算法了) 下面的这些命令是别的博主总结的 GDB 调试过程_gdb调试过程_麷飞花的博客-CSDN博客…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
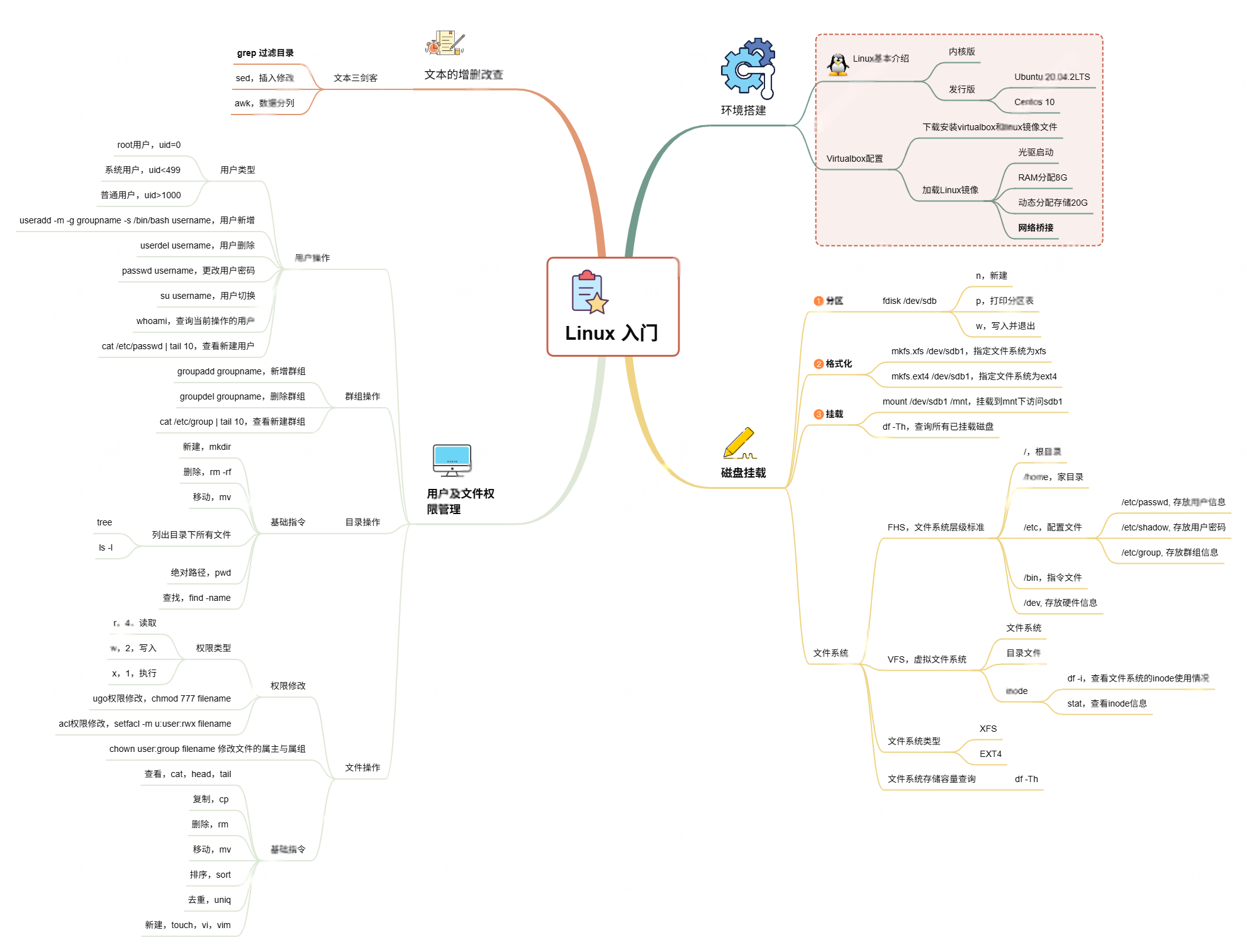
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...
