leetcode重点题目分类别记录(二)基本算法:二分,位图,回溯,动态规划,图论基础,拓扑排序
layout: post
title: leetcode重点题目分类别记录(二)基本算法:二分,位图,回溯,动态规划,拓扑排序
description: leetcode重点题目分类别记录(二)基本算法:二分,位图,回溯,动态规划,拓扑排序
tag: 数据结构与算法
基本算法:二分,位图,回溯,动态规划,图搜索,拓扑排序
- 二分查找
- 搜索插入位置
- 搜索旋转数组
- 前缀和
- 一维
- 二维
- 差分数组
- 题目应用
- 回溯
- 组合
- 排列
- 分割问题
- 分割回文串
- 复原ip地址
- 子集问题
- 子集2
- 递增子序列
- 子集2的另一种去重方法
- 暴力搜索
- 动态规划
- 背包问题
- 01背包
- 完全背包
- 打家劫舍
- 股票系列
- 子序列类
- 数位dp
- 图搜索
- 广度优先搜索bfs
- 迷宫最近的出口
- 解开密码锁的最少次数
- 双向bfs优化
- 深度优先搜素dfs
- 图论基础及其遍历算法
- 基本概念
- 邻接表和邻接矩阵
- 度
- 加权图
- 无向图
- 图的遍历
- 题目应用
- 可能的路径
- 二分图判断算法
- 概念
- 二分图判断思路
- 题目应用
- 拓扑排序
部分内容来自拉不拉东的算法小抄
二分查找
搜索插入位置
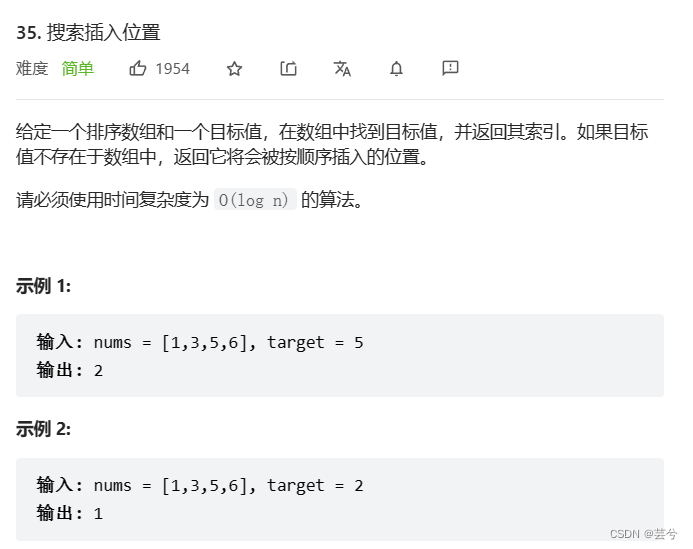
二分查找本质上是排除法的思路,不断将搜索空间缩减为原来的一半,因此整体的时间复杂度为O(LogN),不同的题目需要注意ans的候选位置。
例如本题搜索插入位置,返回插入位置的索引:
如果mid处等于目标值,那么直接返回mid
如果mid处大于目标值,说明目标值应该插在mid左边,那么ans候选位置就是mid;
如果mid处小于目标值,说明目标值应该插入mid右边,那么ans候选位置就是mid+1;
int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1, ans = left;while (left <= right) {int mid = left + ((right - left) >> 1);if (nums[mid] == target) return mid;if (nums[mid] > target) {// target在左边,更新右边界,mid处为可能的插入位置ans = mid;right = mid - 1;} else {// target 在右边,更新左边界,mid + 1处为可能的插入位置left = mid + 1;ans = left;}}return ans;}
搜索旋转数组
基础版:没有重复元素
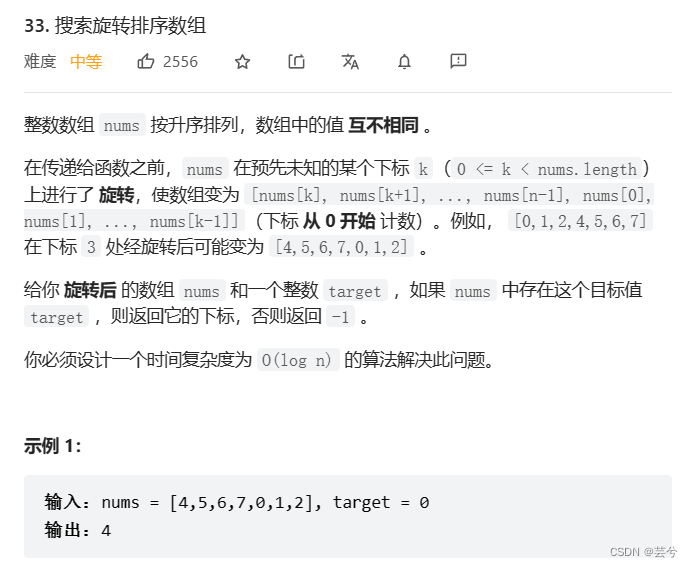
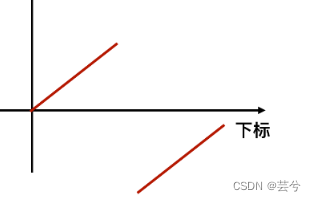
int search(vector<int>& nums, int target) {int left = 0, n = nums.size(), right = n - 1;while (left <= right) {int mid = left + ((right - left) >> 1);if (nums[mid] == target) return mid;if (nums[mid] >= nums[0]) { // 通过与nums[0]比较判断nums[mid]的落点在断点左边或右边// 在断点左边这部分有序区间二分if (target >= nums[0] && target < nums[mid]) right = mid - 1; // 如果目标值与中间值在同一部分有序区间,可以排除一半,并进入有序空间的排序else left = mid + 1; // 即使不在同一部分,也可以缩减搜索整个区间的范围} else {// 在断点右边这部分有序区间二分if (target > nums[mid] && target <= nums[right]) left = mid + 1;else right = mid - 1;}}return -1;}
前缀和
前缀和适用于很快的求解某个区间的累计和
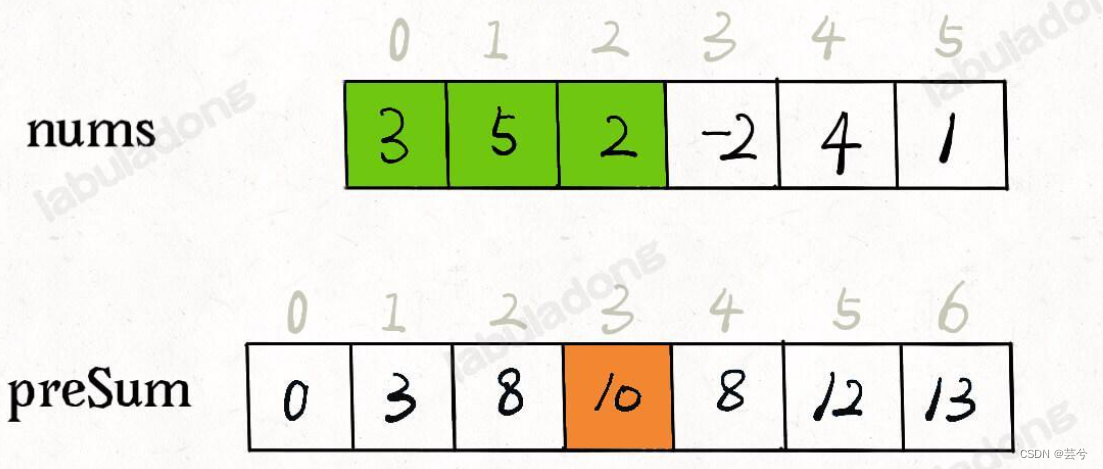
一维
preSum[i]记录前i个数的累计和,i从0开始,那么
preSum[right] - preSum[left] 就是左闭右开区间[left, right)的nums子数组和。
二维

仿照一维的思路,用pre[i + 1][j + 1]表示从左上角到下标(i,j)位置表示的右下角位置间区域的累计和。
那么任意一个矩形区间的累计和可标记为:
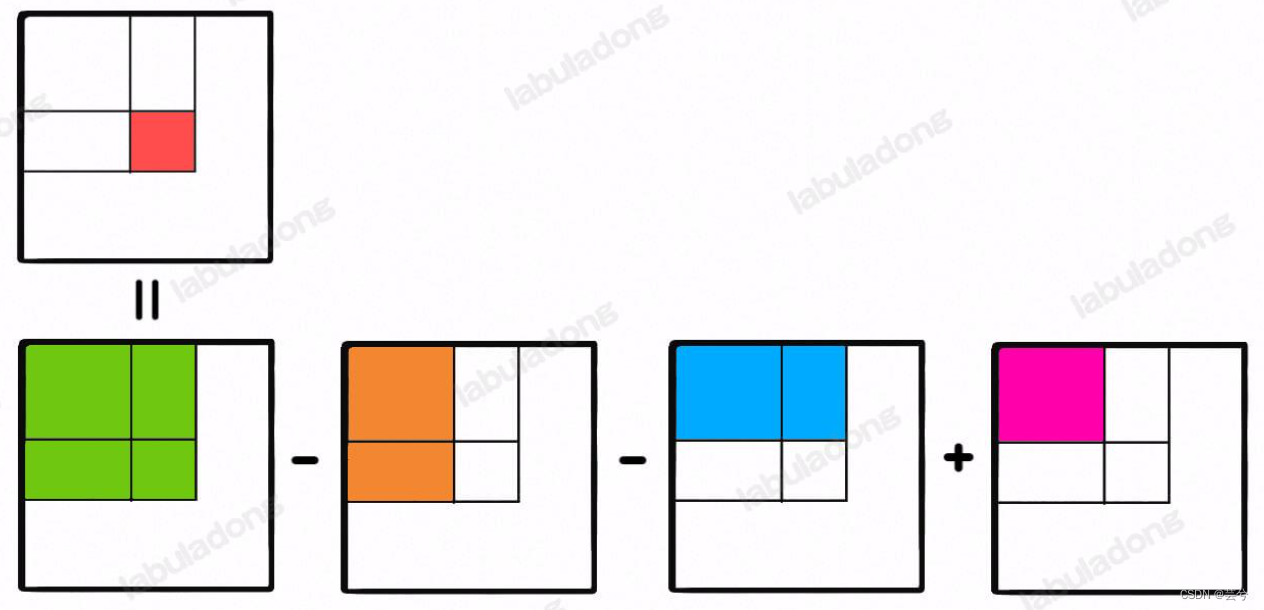
注意:在下边的代码中,在计算累加时的方法为:
presum[i + 1][j + 1] = presum[i + 1][j] + presum[i][j + 1] + matrix[i][j] - presum[i][j];
左上角部分加了两次,要减去
而计算区间时,左上角部分减了两次要加回来:
presum[row2 + 1][col2 + 1] + presum[row1][col1] - presum[row1][col2 + 1] - presum[row2 + 1][col1];
class NumMatrix {
public:vector<vector<int>> presum;NumMatrix(vector<vector<int>>& matrix) {int m = matrix.size(), n = matrix[0].size();presum = vector<vector<int>>(m + 1, vector<int>(n + 1));for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {presum[i + 1][j + 1] = presum[i + 1][j] + presum[i][j + 1] + matrix[i][j] - presum[i][j];}}}int sumRegion(int row1, int col1, int row2, int col2) {return presum[row2 + 1][col2 + 1] + presum[row1][col1] - presum[row1][col2 + 1] - presum[row2 + 1][col1]; }
};
差分数组
差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
差分数组的求法:
第一个数与nums[0],后边每个数等于该处下标 减去 前一个下标。
后减去前,第一个位置前面没有,故是本身
diff[0] = nums[0];
diff[i] = nums[i] - nums[i - 1];
可以发现,根据差分数组diff可以还原出nums数组,具体做法就是对差分数组diff求累计和
因为是求累计和,所以假定我们给diff数组i位置处增减一个元素值,那么它后边位置处都会增减该元素值。
具体的,假定你要让左闭右开区间[left, right)上的元素都加上k, 那么只需令差分数组diff[left] += k,diff[right] -= k;
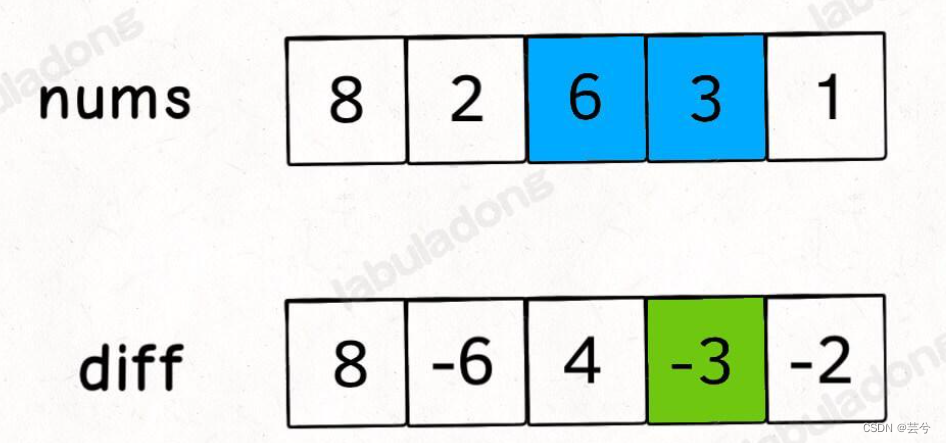
我们可以将上述过程写成一个封装的类,输入一个nums数组,设置increament方法。
特别需要注意的是:
构建差分数组diff[]时,需要右减左,而恢复时是需要累加。
class Difference {public:vector<int> diff;Difference(const vector<int> &nums){diff = nums;for (int i = 1; i < nums.size(); ++i) {diff[i] -= nums[i - 1]; }}// 给左闭右开区间[i, j) 增加val,val可以是负数void increment(int i, int j, int val) {diff[i] += val;if (j < diff.size()) diff[j] -= val;}vector<int> getResult() {vector<int> res(diff);for (int i = 1; i < res.size(); ++i) {res[i] += res[i - 1];}return res;}
};
题目应用
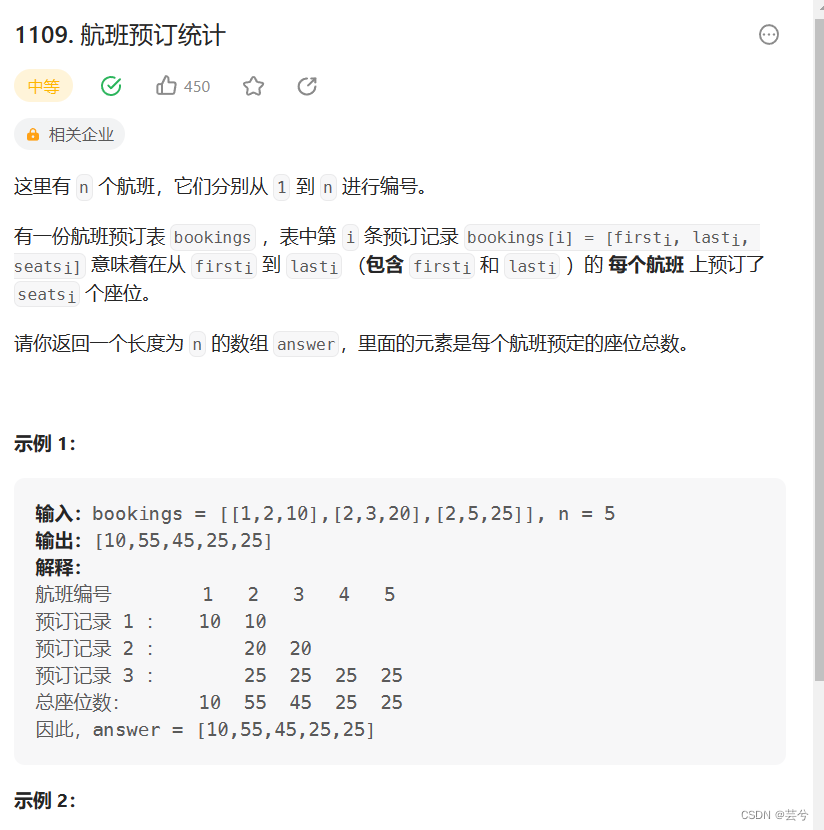
分析题意,其实就是初始answer都是0,根据bookings,将对应区间都加上座位数。
可以直接利用上边写的差分数组类:
注意我们写的时候,是对左必右开区间,同时增加。
而题目的意思是左右闭区间,此外航班序号比索引号大1.
vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {vector<int> nums(n);Difference d(nums);for (int i = 0; i < bookings.size(); ++i) {int x = bookings[i][0] - 1, y = bookings[i][1], val = bookings[i][2];d.increment(x, y, val);}return d.getResult();}
回溯
组合
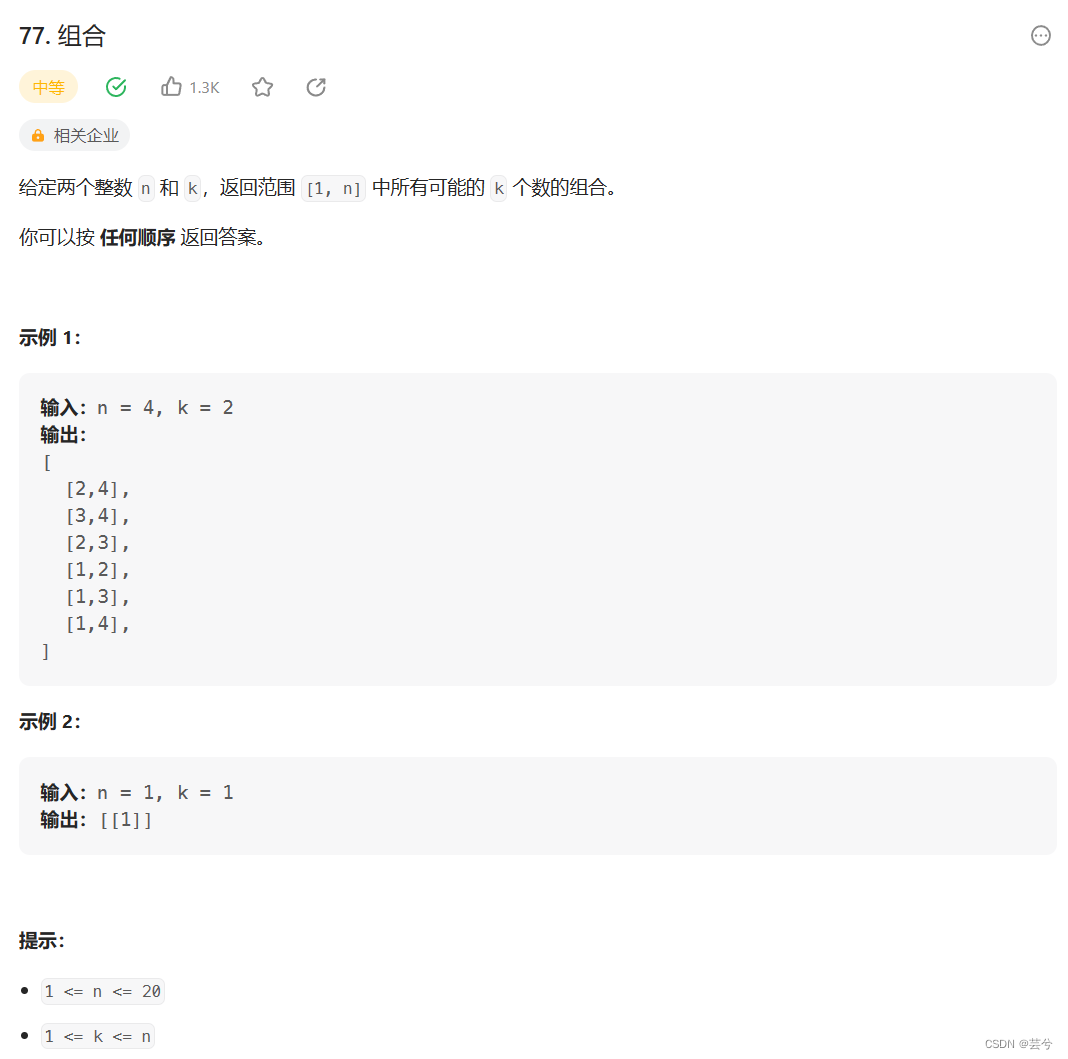
注意剪枝:
当前可选的数据范围为[i, n] 有 n - i + 1个
还需要的数据个数为 k - path.size();
可选范围必须大于等于所需的元素。
vector<vector<int>> combine(int n, int k) {vector<vector<int>> ans;vector<int> path;function<void(int)> backtracking = [&](int index) {if (path.size() == k) {ans.push_back(path);return;}for (int i = index; i <= n && path.size() + n - i + 1 >= k; ++i) {path.push_back(i);backtracking(i + 1);path.pop_back();}};backtracking(1);return ans;}
排列
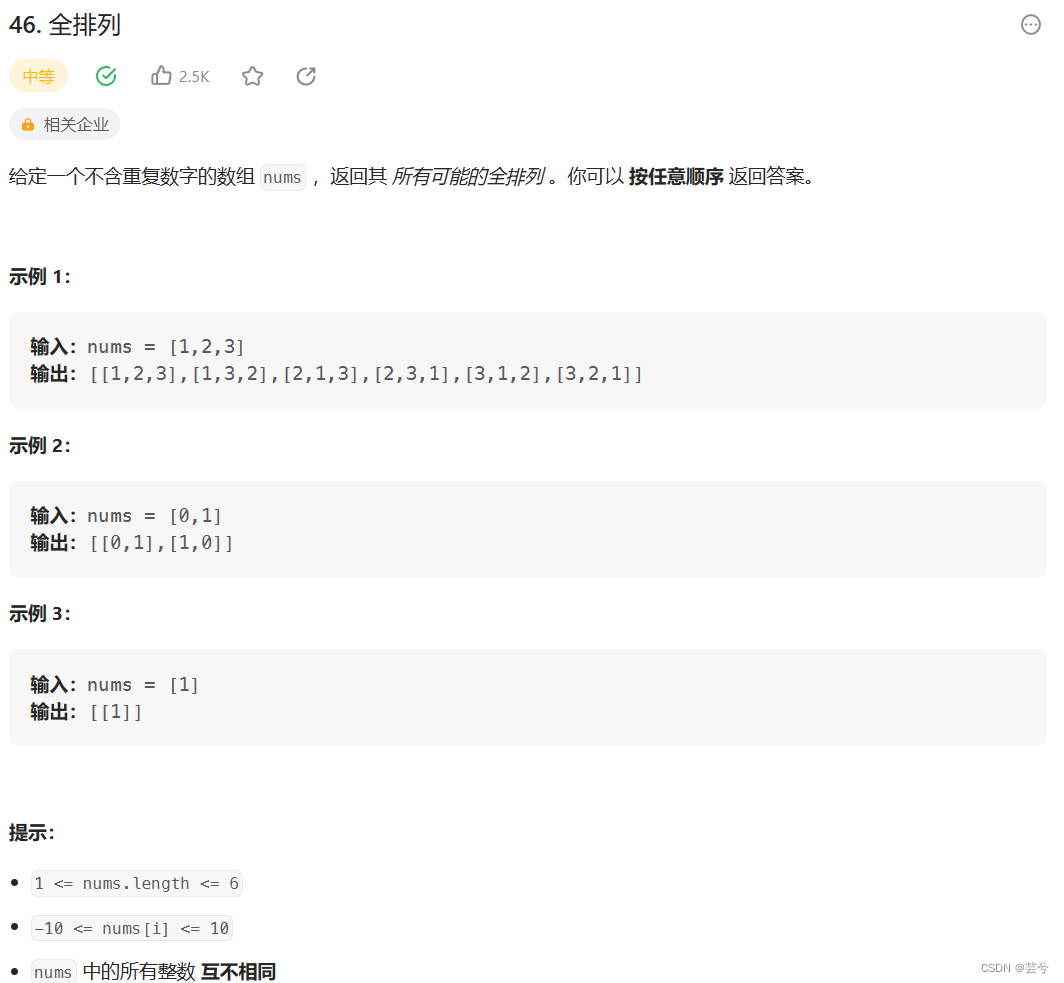
排序问题与组合问题最大的区别在于,前边的选择是否影响后边的选择
比如:1,2,3
如果第一步选择了2,那么后边可选的只剩下3
而排列中,第一步选择了2,后边还是可以选择1或3
对应在代码中,组合问题一般回溯到下一层传递的是 i + 1,i是当前选择的位置,而排序则是index + 1,按照 index即层序来更新,而非当前选择的位置i。
vector<vector<int>> permute(vector<int>& nums) {vector<vector<int>> ans;function<void(int)> dfs = [&] (int index) {if (index == nums.size()) {ans.push_back(nums);return;}for (int i = index; i < nums.size(); ++i) {swap(nums[i], nums[index]);dfs(index + 1);swap(nums[i], nums[index]);}};dfs(0);return ans;}
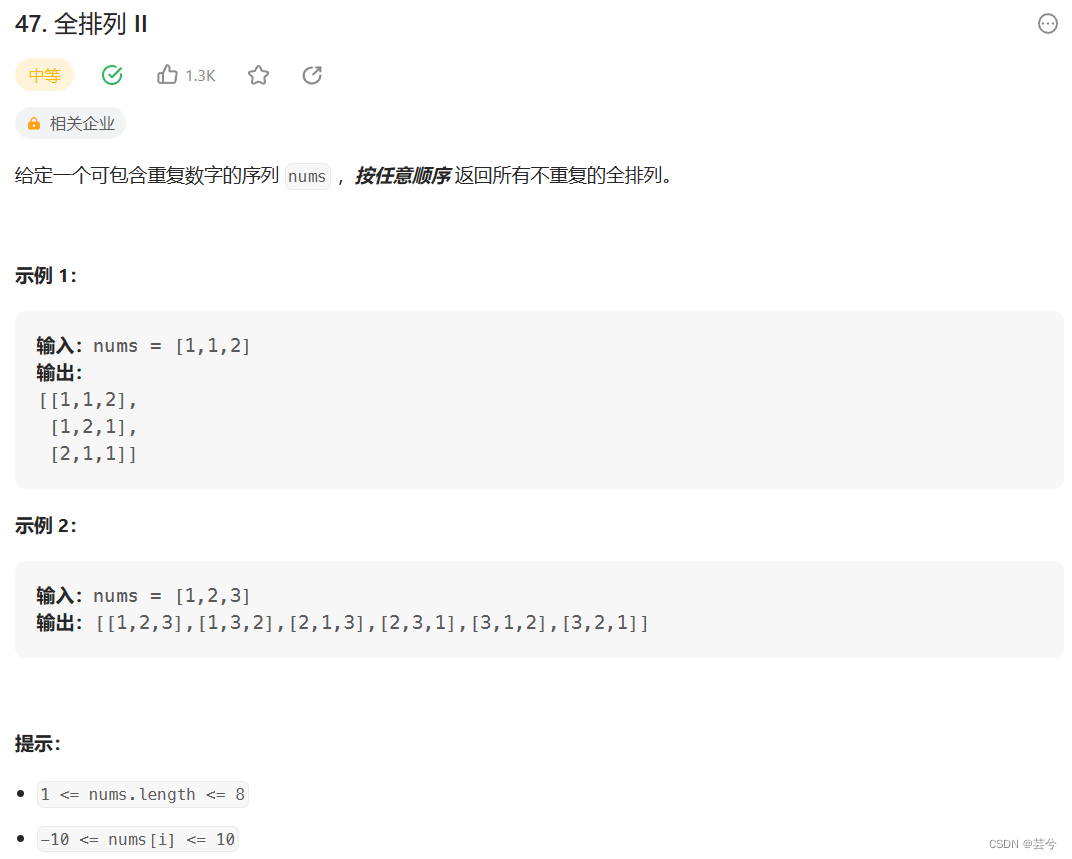
有重复情况下的排列去重逻辑与组合一样。与组合不同的地方在于,每个位置都有可能添加到当前path的末尾,因此需要一个used数组,然后每次遍历整个nums。
vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(), nums.end());vector<vector<int>> ans;vector<int> path;vector<bool> used(nums.size(), false);function<void()> dfs = [&] () {if (path.size() == nums.size()) {ans.push_back(path);return;}for (int i = 0; i < nums.size(); ++i) {if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;if (used[i] == false) {path.push_back(nums[i]);used[i] = true;dfs();path.pop_back();used[i] = false;}}};dfs();return ans;}
分割问题
分割回文串
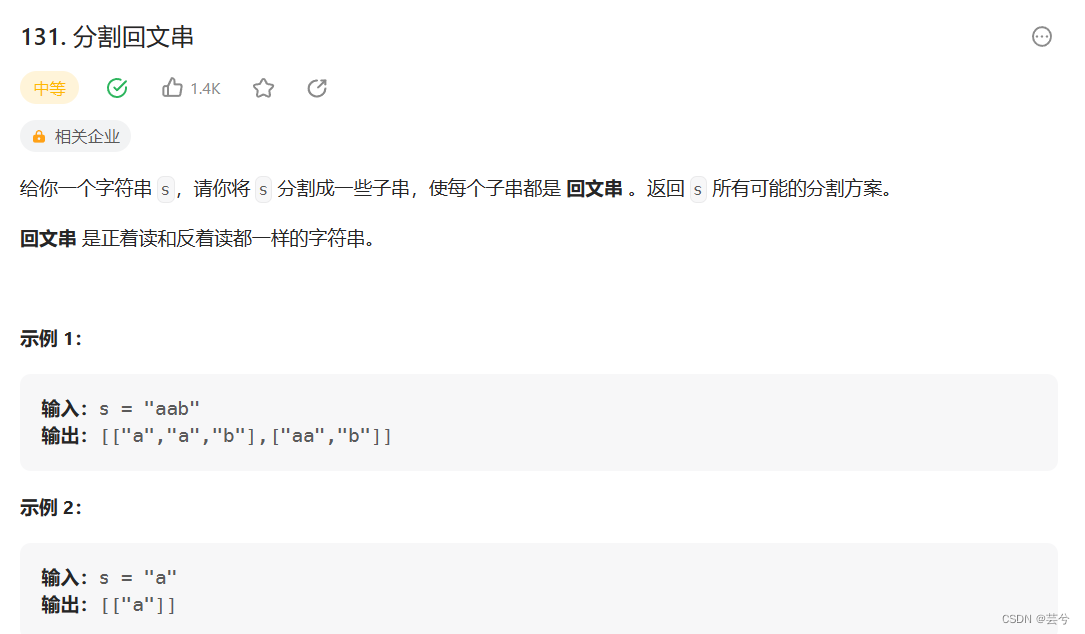
分割问题的本质为确定分割线的位置可能;
根据一个起始的分割点,枚举所有可能的下一个分割点,如果当前分割出了回文串,进入更深层次的搜索。
class Solution {
public:vector<vector<string>> partition(string s) {vector<vector<string>> ans;vector<string> path;function<void(int)> dfs = [&](int index) {if (index == s.size()) {ans.push_back(path);return;}for (int i = index; i < s.size(); ++i) {string str = s.substr(index, i - index + 1);if (isValid(str)) {path.push_back(str);dfs(i + 1);path.pop_back();}}};dfs(0);return ans;}bool isValid(const string &str) {for (int i = 0, j = str.size() - 1; i <= j; ++i, --j) {if (str[i] != str[j]) return false;}return true;}
};
复原ip地址
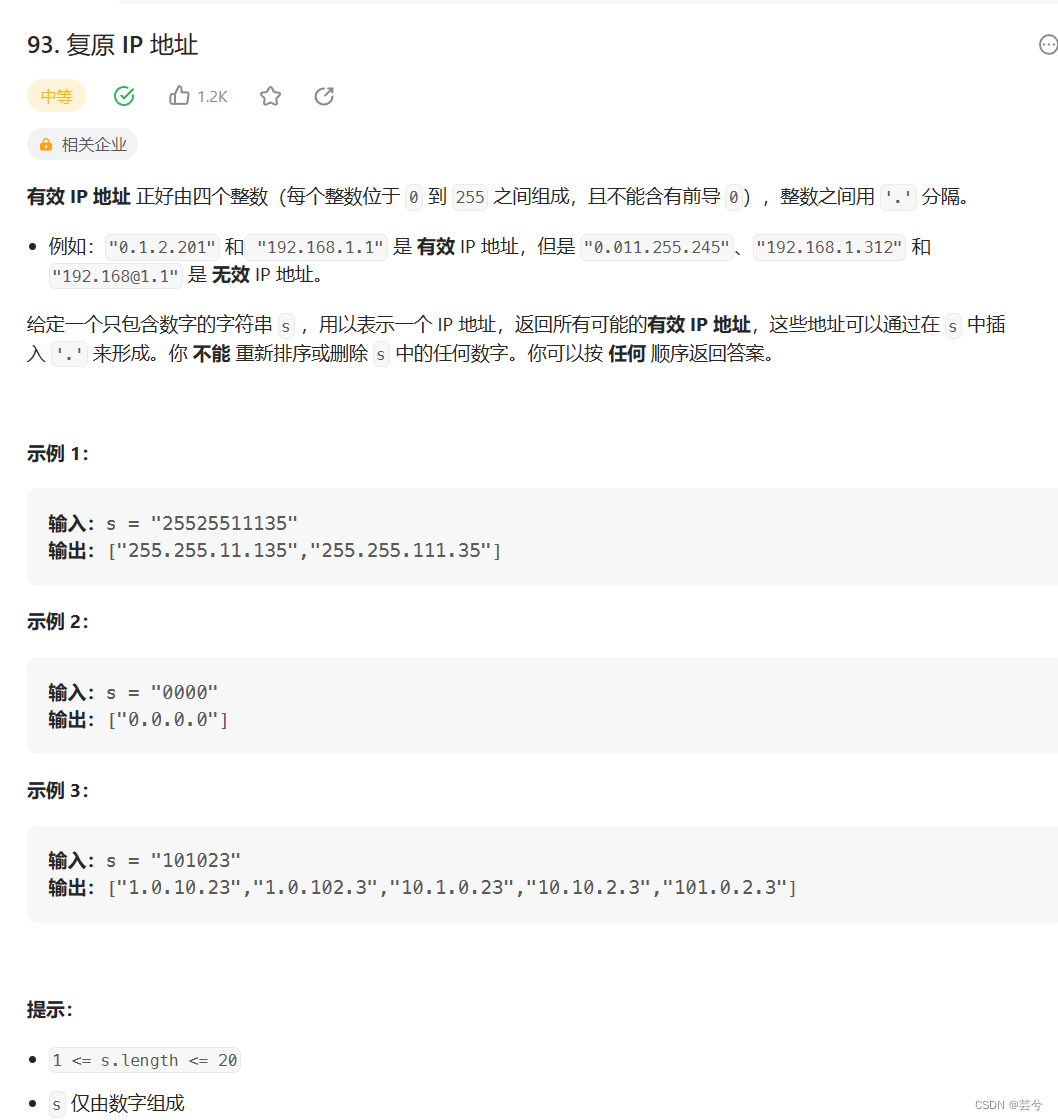
复原ip地址问题,同样是确定分割点,这里比较复杂的地方在于剪枝。
class Solution {
public:vector<string> restoreIpAddresses(string s) {vector<string> ans;vector<string> path;if (s.size() < 4 || s.size() > 12) return ans;function<void(int)> dfs = [&](int index) {// 根据当前位置和剩余的字符确定剩余部分是否能够构成一个有效的部分int leftPart = 4 - path.size(), leftChar = s.size() - index;if (leftChar < leftPart || leftChar > 3 * leftPart) return;if (path.size() == 3) {string leftStr = s.substr(index, leftChar);if (isValid(leftStr)) {string res;for (string str : path) res += str + ".";res += leftStr;ans.push_back(res);}return;}// i < index + 3 保证了分割出的子串长度小于等于3for (int i = index; i < s.size() && i < index + 3; ++i) {string str = s.substr(index, i - index + 1);if (isValid(str)) {path.push_back(str);dfs(i + 1);path.pop_back();}}};dfs(0);return ans;}bool isValid(const string &str) {if (str.size() == 1) return true;if (str[0] == '0') return false;int num = 0;for (char c : str) num = num * 10 + (c - '0');return num <= 255;}
};
子集问题
子集2
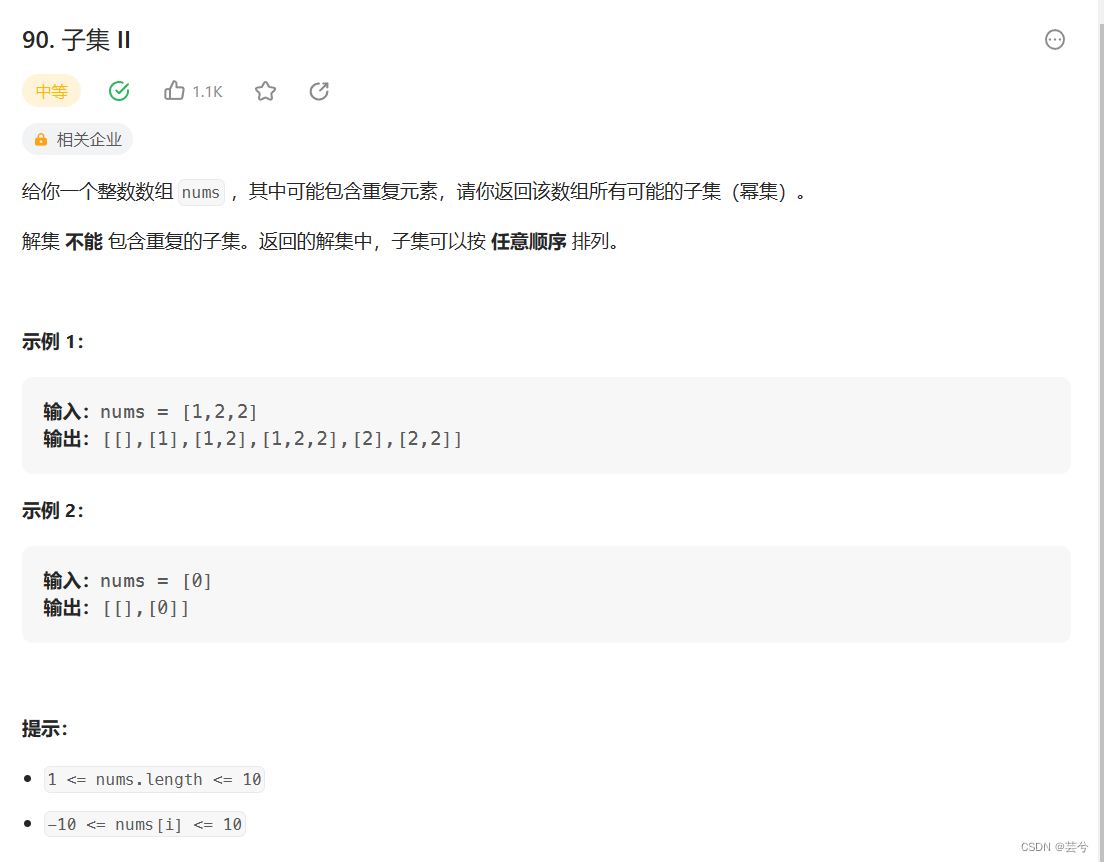
子集问题与回溯中其他问题最大的区别在于,不需要设置回溯的终点,因为回溯路径上每一个节点都是最终所需的一个path;因此上来就需要将当前path加入到ans中,且不能return,选或者不选都是一种子集可能的情况。
vector<vector<int>> subsetsWithDup(vector<int>& nums) {vector<vector<int>> ans;vector<int> path;sort(nums.begin(), nums.end());vector<bool> used(nums.size(), false);function<void(int)> dfs = [&] (int index) {ans.push_back(path);for (int i = index; i < nums.size(); ++i) {if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;path.push_back(nums[i]);used[i] = true;dfs(i + 1);path.pop_back();used[i] = false;}};dfs(0);return ans;}
递增子序列
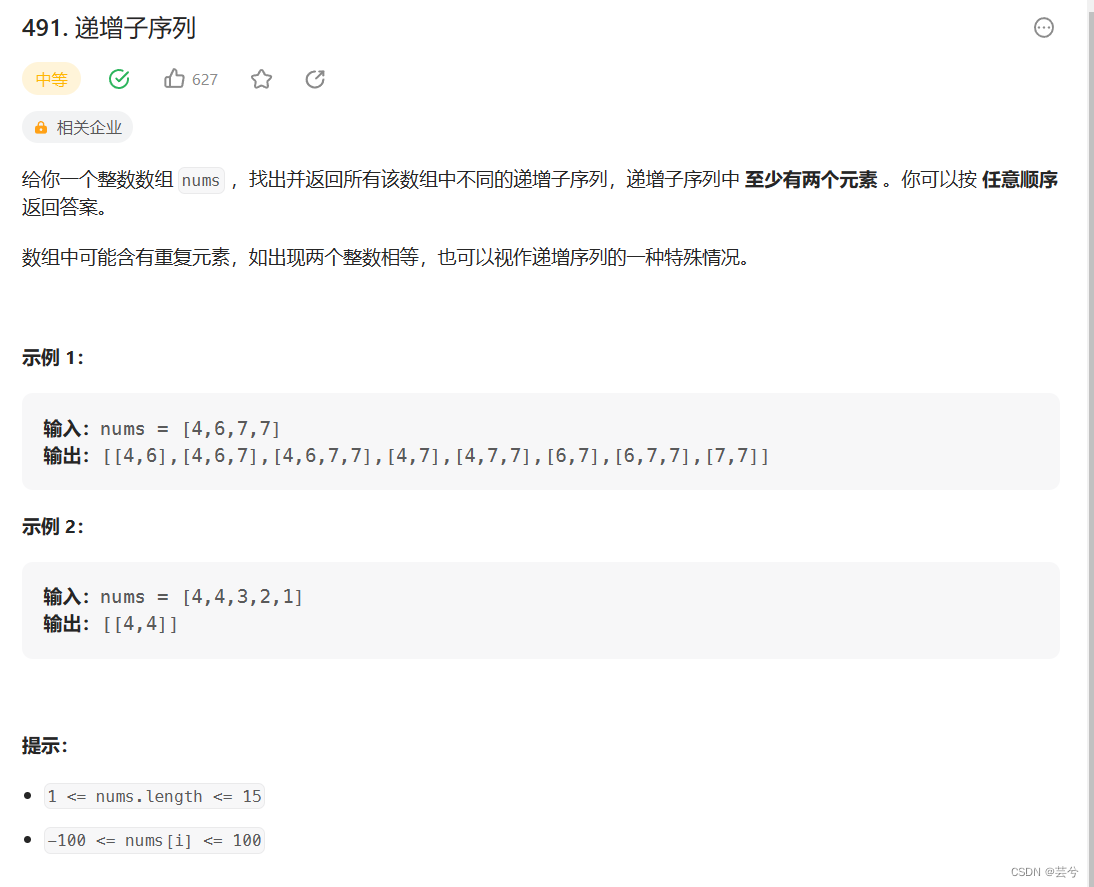
该题与子集2有相似的地方:每次需要取路径树上的节点,即选或者不选都是一种可能,回溯开始就考虑是否将path添加到ans中;
另一个相似的地方在于需要去重。
这一题去重的逻辑比子集稍微复杂一些,首先它也是在当前层去重,当前层如果已经选择了某个元素,当前层的后边节点就不可以在使用。
但是子集2中,不要求输出顺序,因此可以对其进行排序,把重复元素堆在一块儿。
这里则不行,需要使用一个单独的hash表来记录当前层使用了哪些元素。注意这里的hash表只对当前回溯过程中当前层使用,与used数组不同!!!
vector<vector<int>> findSubsequences(vector<int>& nums) {vector<vector<int>> ans;vector<int> path;int n = nums.size();function<void(int)> dfs = [&] (int index) {if (path.size() > 1) ans.push_back(path);int hash[201] = {0};for (int i = index; i < n; ++i) {if ((!path.empty() && path.back() > nums[i]) || hash[nums[i] + 100] == 1) continue;path.push_back(nums[i]);hash[nums[i] + 100] = 1;dfs(i + 1);path.pop_back();}};dfs(0);return ans;}
子集2的另一种去重方法
子集问题实际上也可以使用上边这种在单层使用hash表记录的形式。
并且我认为这种形式实际上更加直观易懂!!!
vector<vector<int>> subsetsWithDup(vector<int>& nums) {vector<vector<int>> ans;vector<int> path;sort(nums.begin(), nums.end());function<void(int)> dfs = [&] (int index) {ans.push_back(path);int hash[21] = {0};for (int i = index; i < nums.size(); ++i) {if (hash[nums[i] + 10] == 1) continue;path.push_back(nums[i]);hash[nums[i] + 10] = 1;dfs(i + 1);path.pop_back();}};dfs(0);return ans;}
暴力搜索
动态规划
背包问题
01背包
完全背包
打家劫舍
股票系列
子序列类
数位dp
图搜索
广度优先搜索bfs
广度优先搜索最经典的题目就是二叉树的层序遍历。
广度优先搜索的问题的本质就是让你在一幅图中找到从起点start到终点target的最近距离。
迷宫最近的出口

思路:每次有四个方向可以选择,使用bfs搜索,将非墙的位置加入到队列中。为了避免走重复的路,在加入队列后,将相应位置标记为墙。当来到边界位置处,边是最近的出口。为了记录距离,可以把位置距离起点的距离同时记录到队列中的节点。
int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {int m = maze.size(), n = maze[0].size();const int dx[4] = {1, -1, 0 , 0}, dy[4] = {0, 0, 1, -1}; // 偏移量数组queue<tuple<int, int, int>> que; // 包含位置x,y和距离起点距离的节点队列que.emplace(entrance[0], entrance[1], 0); maze[entrance[0]][entrance[1]] = '+'; // 每次加入队列后,将位置改为墙,避免重复while (!que.empty()) {auto [x, y, d] = que.front();que.pop();for (int i = 0; i < 4; ++i) {int cx = x + dx[i], cy = y + dy[i];if (cx >= 0 && cx < m && cy >= 0 && cy < n && maze[cx][cy] == '.') { // 只有相邻位置可走才进行判断与加入队列的操作if (cx == 0 || cx == m - 1 || cy == 0 || cy == n - 1) return d + 1; // 如果其中一个有效相邻位置为边缘处,说明找到出口了que.emplace(cx, cy, d + 1);maze[cx][cy] = '+'; // 每次加入队列后,将位置改为墙,避免重复}}}return -1;}
解开密码锁的最少次数

class Solution {
public:// 将i位置数字加一string plusone(string s, int i) {if (s[i] == '9') {s[i] = '0';return s;}++s[i];return s;}// 将i位置数字减一string minusone(string s, int i) {if (s[i] == '0') {s[i] = '9';return s;}--s[i];return s;}int openLock(vector<string>& deadends, string target) {const string root = "0000";if (target == root) return 0; // 如果目标值就是当前值,直接返回unordered_set<string> visited;for (string &str : deadends) visited.insert(str); // 死亡数字相当于已经访问过,不能再访问queue<string> que;if (!visited.count(root)) { // 只有非访问过的节点才能加入队列,入队即访问que.push(root);visited.insert(root);}int ans = 0;while (!que.empty()) {int sz = que.size();for (int i = 0; i < sz; ++i) {string cur = que.front();que.pop();for (int j = 0; j < 4; ++j) { // 四个数字轮流上下转动string plus = plusone(cur, j);if (plus == target) return ans + 1; // 如果转到target,返回ans + 1if (!visited.count(plus)) { // 只有非访问过的节点才能加入队列,入队即访问que.push(plus);visited.insert(plus);}string minus = minusone(cur, j);if (minus == target) return ans + 1;if (!visited.count(minus)) { // 只有非访问过的节点才能加入队列,入队即访问que.push(minus);visited.insert(minus);}}}++ans;}return -1;}
};
双向bfs优化
传统的 BFS 框架就是从起点开始向四周扩散,遇到终点时停止;而双向 BFS 则是从起点和终点同时开始扩散,当两边有交集的时候停止。
因为双向bfs需要从两头开始扩散,因此必须指定目标点位置!
传统bfs是从起点位置不断向周围扩散,直至扩散至目标处。
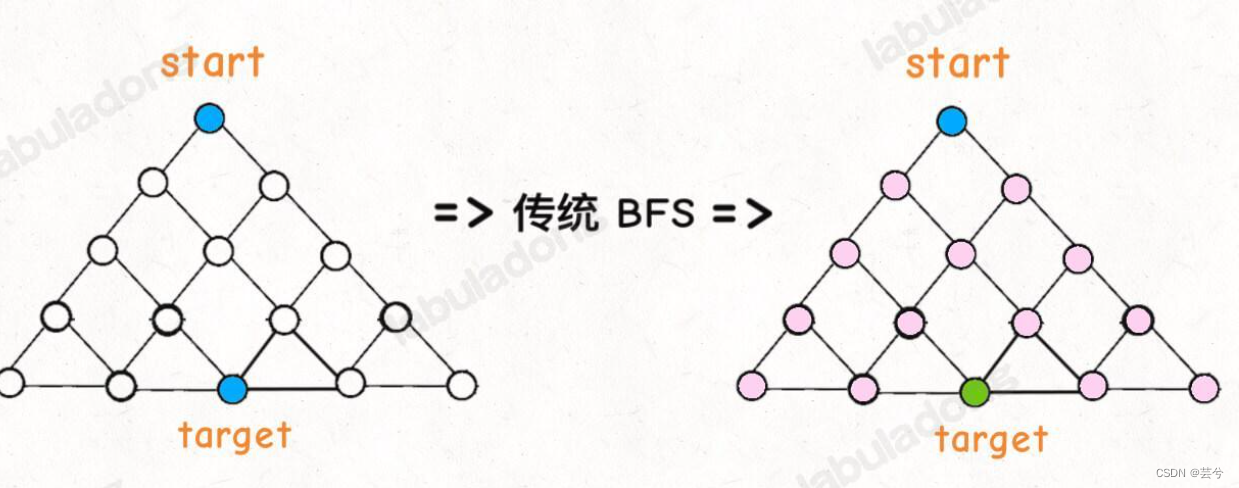
双向bfs从起点和终点两头扩散,看最终是否能够有交集。
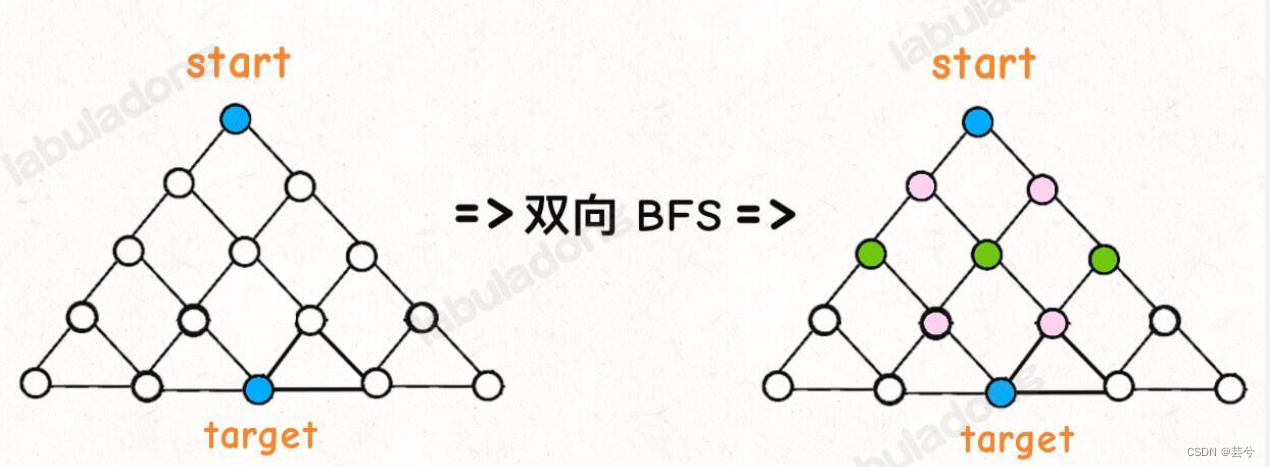
深度优先搜素dfs
图论基础及其遍历算法
基本概念
邻接表和邻接矩阵
邻接表和邻接矩阵是存储图结构的两种主要的方式方式:
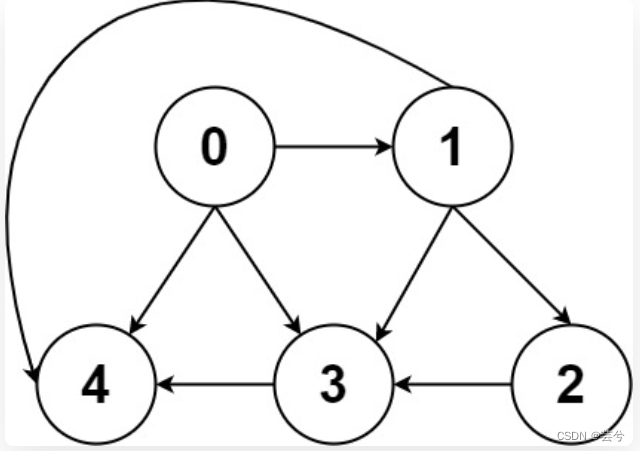
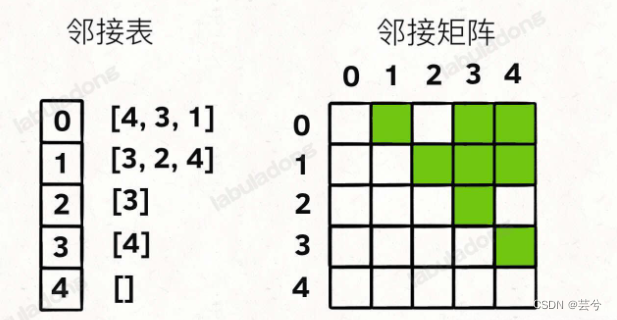
邻接表很直观,把每个节点x的邻居都存到一个列表里,然后把x和这个列表关联起来,这样就可以通过一个节点x找到它的所有相邻节点。
邻接矩阵则是一个二维布尔数组,我们权且称为matrix,如果节点x和y是相连的,那么就把matrix[x][y]设为true,如果想找节点x的邻居,那么遍历一遍matrix[x][…]就够了。
代码形式如下:
// 邻接表
// graph[x] 存储 x 的所有邻居节点
vector<int> graph[];// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
bool matrix[][];邻接表的优点在于占用空间少,因为邻接矩阵有很多空余空间浪费。但是邻接表无法快速判断两个节点是否相邻,而临界矩阵却可以。因此两种形式各有利弊,使用时需结合具体情况。
度
在无向图中,度就是每个节点相连的边的条数,由于有向图的边是有方向的,因此每个节点的度又被细分为出度和入度。
加权图
有时图中还需要存储每个节点与相邻节点间的权重(距离),对于这种加权图:
如果采用邻接表的形式存储,在储存邻居点标号的同时,还需记录对应的权重;
如果采用邻接矩阵,那么matrix[x][y]不再是布尔值,而是一个int值,0表示没有连接,其他值表示权重。
代码形式如下:
vector<pair<int, int>> graph[];// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重,0 表示不相邻
vector<vector<int>> matrix;
无向图
如果是无向图,其实等同于每个相邻节点是双向的。
如果连接无向图中的节点 x 和 y,把 matrix[x][y] 和 matrix[y][x] 都变成 true 不就行了;邻接表也是类似的操作,在 x 的邻居列表里添加 y,同时在 y 的邻居列表里添加 x。
把上面的技巧合起来,就变成了无向加权图。
图的遍历
图的遍历与多叉树是类似的,使用dfs遍历图可能是包含环的,为了避免重复遍历,需要一个visited数组进行辅助,如果题目告诉了不包含环,那么可以去掉visited数组
void traverse(TreeNode root) {if (root == null) return;for (TreeNode child : root.children) {printf("进入节点 %s", child);traverse(child);printf("离开节点 %s", child);}
}
如果执行上边的遍历算法,会发现这种方式会把根节点遗漏,为了避免遗漏,我们应该将打印时机放在for循环外部:
void traverse(TreeNode root) {if (root == null) return;printf("进入节点 %s", root);for (TreeNode child : root.children) {traverse(child);}printf("离开节点 %s", root);
}
题目应用
可能的路径
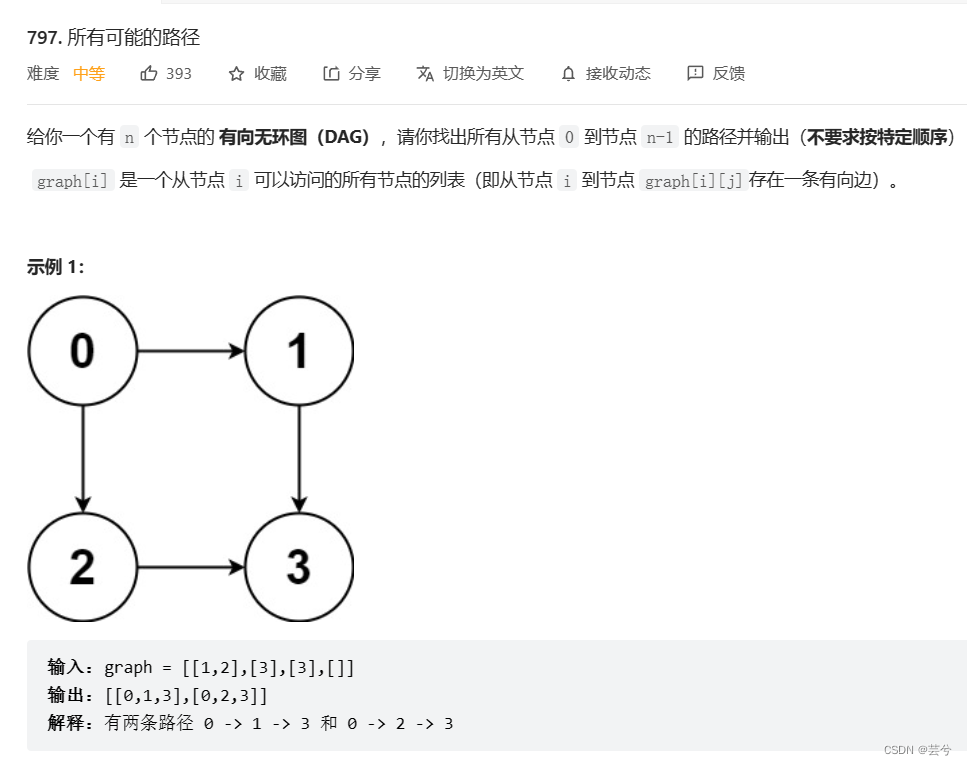
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {vector<vector<int>> ans;vector<int> path;int n = graph.size();// 根据遍历起始点,搜索下一步可以到达的位置function<void(int)> traverse = [&] (int cur) {// 记录path.push_back(cur);if (cur == n - 1) {ans.push_back(path);}for (int c : graph[cur]) traverse(c);// 撤销当前的记录path.pop_back();};traverse(0);return ans;}
二分图判断算法
概念
二分图的定义:
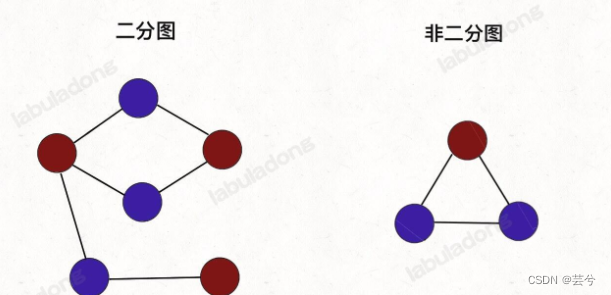
二分图的顶点集可分割为两个互不相交的子集,图中每条边依附的两个顶点都分属于这两个子集,且两个子集内的顶点不相邻。
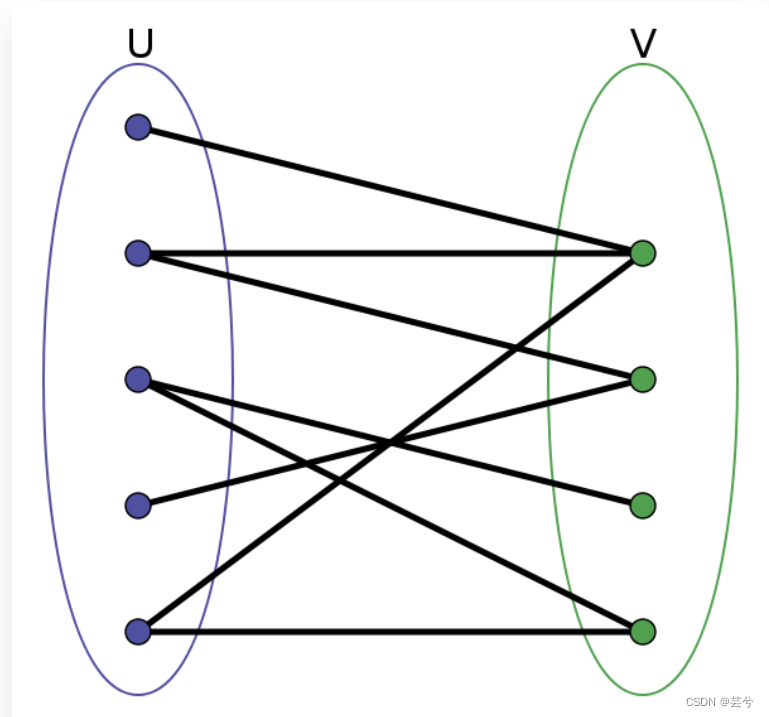
从定义上不太好理解,但可以用双色问题来等同于二分图问题。
给你一幅「图」,请你用两种颜色将图中的所有顶点着色,且使得任意一条边的两个端点的颜色都不相同,你能做到吗?
如果能,那么这幅图就是二分图,反之则不是。
从简单实用的角度来看,二分图结构在某些场景可以更高效地存储数据。
比如说我们需要一种数据结构来储存电影和演员之间的关系:某一部电影肯定是由多位演员出演的,且某一位演员可能会出演多部电影。
既然是存储映射关系,最简单的不就是使用哈希表嘛,我们可以使用一个 HashMap<String, List> 来存储电影到演员列表的映射,如果给一部电影的名字,就能快速得到出演该电影的演员。
但是如果给出一个演员的名字,我们想快速得到该演员演出的所有电影,怎么办呢?这就需要「反向索引」,对之前的哈希表进行一些操作,新建另一个哈希表,把演员作为键,把电影列表作为值。
显然,如果用哈希表存储,需要两个哈希表分别存储「每个演员到电影列表」的映射和「每部电影到演员列表」的映射。但如果用「图」结构存储,将电影和参演的演员连接,很自然地就成为了一幅二分图:
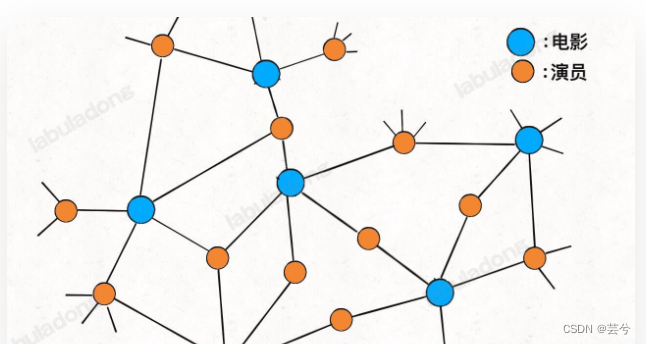
每个电影节点的相邻节点就是参演该电影的所有演员,每个演员的相邻节点就是该演员参演过的所有电影,非常方便直观。
其实生活中不少实体的关系都能自然地形成二分图结构,所以在某些场景下图结构也可以作为存储键值对的数据结构(符号表)。
二分图判断思路
判定二分图的算法很简单,就是用代码解决「双色问题」。
说白了就是遍历一遍图,一边遍历一边染色,看看能不能用两种颜色给所有节点染色,且相邻节点的颜色都不相同。
// 二叉树遍历框架
void traverse(TreeNode* root) {if (root == nullptr) return;traverse(root->left);traverse(root->right);
}// 多叉树遍历框架
void traverse(Node* root) {if (root == nullptr) return;for (Node* child : root->children)traverse(child);
}// 图遍历框架
vector<bool> visited;
void traverse(Graph* graph, int v) {// 防止走回头路进入死循环if (visited[v]) return;// 前序遍历位置,标记节点 v 已访问visited[v] = true;for (Vertex neighbor : graph->neighbors(v))traverse(graph, neighbor);
}因为图中可能存在环,所以用 visited 数组防止走回头路。
这里可以看到我习惯把 return 语句都放在函数开头,因为一般 return 语句都是 base case,集中放在一起可以让算法结构更清晰。
回顾一下二分图怎么判断,其实就是让 traverse 函数一边遍历节点,一边给节点染色,尝试让每对相邻节点的颜色都不一样。
所以,判定二分图的代码逻辑可以这样写:
// 图遍历框架
void traverse(Graph graph, bool visited[], int v) {visited[v] = true;// 遍历节点 v 的所有相邻节点 neighborfor (int neighbor : graph.neighbors(v)) {if (!visited[neighbor]) {// 相邻节点 neighbor 没有被访问过// 那么应该给节点 neighbor 涂上和节点 v 不同的颜色traverse(graph, visited, neighbor);} else {// 相邻节点 neighbor 已经被访问过// 那么应该比较节点 neighbor 和节点 v 的颜色// 若相同,则此图不是二分图}}
}题目应用
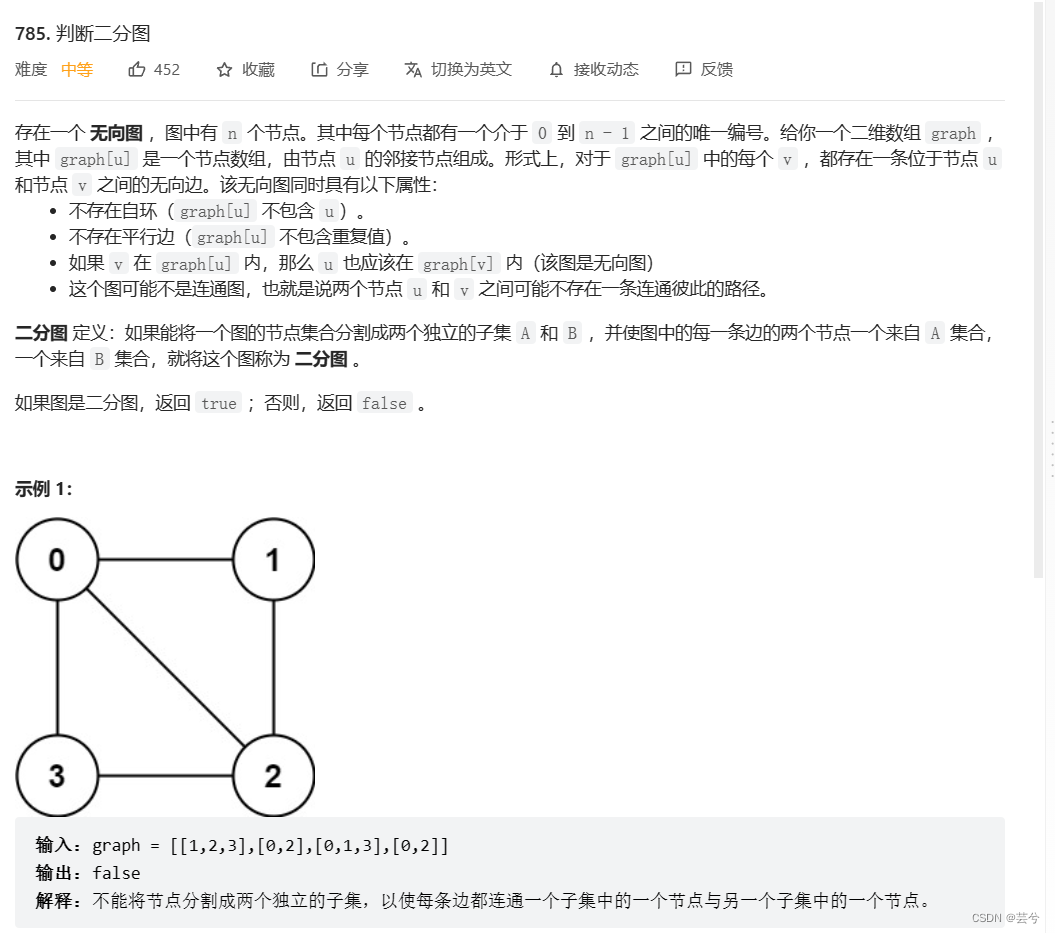
bool isBipartite(vector<vector<int>>& graph) {int n = graph.size();vector<bool> visit(n, false), color(n, false);bool ans = true;function<void(int)> dfs = [&](int cur) {if (!ans) return; // 如果已经非二分图了,直接返回,不需要再遍历了if (visit[cur]) return; // 遍历过的跳过,避免环路重复遍历visit[cur] = true;for (int nb : graph[cur]) {if (!visit[nb]) {// 如果相邻节点没有被访问过,那么给neighbor涂上与cur不一样的颜色color[nb] = !color[cur];dfs(nb); // 接着遍历} else {// 如果相邻节点访问过了,判断它与cur是否颜色不一样,如果一样说明不是二分图if (color[cur] == color[nb]) {ans = false;return;}}}};// 因为图不一定是连通的,可能存在多个子图,所以要把每个节点都作为起点进行一次遍历,如果任意一个子图不是二分图,整个图都不算是二分图for (int v = 0; v < n; ++v) {if (!visit[v]) {dfs(v);}if (!ans) return false; // 如果从某个节点处开始遍历,发现已经出现非二分图了,直接返回false}return true;}
拓扑排序
相关文章:

leetcode重点题目分类别记录(二)基本算法:二分,位图,回溯,动态规划,图论基础,拓扑排序
layout: post title: leetcode重点题目分类别记录(二)基本算法:二分,位图,回溯,动态规划,拓扑排序 description: leetcode重点题目分类别记录(二)基本算法:二…...

【JaveEE】多线程之定时器(Timer)
目录 1.定时器的定义 2.标准库中的定时器 2.1构造方法 2.2成员方法 3.模拟实现一个定时器 schedule()方法 构造方法 4.MyTimer完整代码 1.定时器的定义 定时器也是软件开发中的一个重要组件. 类似于一个 "闹钟". 达到一个设定的时间之后, 就执行某个指…...
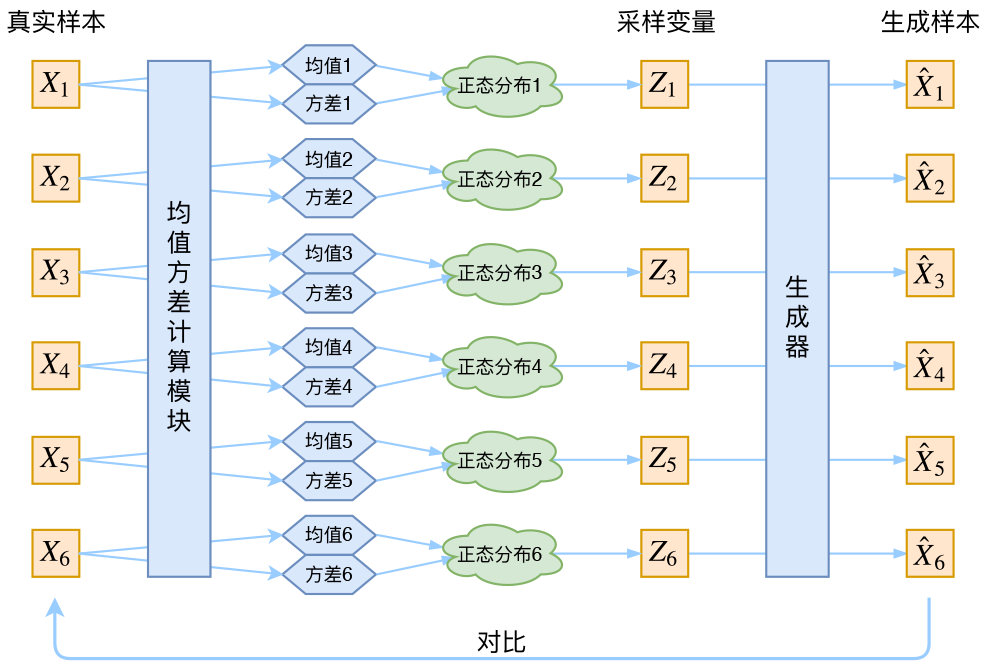
【理论推导】变分自动编码器 Variational AutoEncoder(VAE)
变分推断 (Variational Inference) 变分推断属于对隐变量模型 (Latent Variable Model) 处理的一种技巧,其概率图如下所示 我们将 X{x1,...xN}X\{ x_1,...x_N \}X{x1,...xN} 看作是每个样本可观测的一组数据,而将对应的 Z{z1,...,zN}Z\{z_1,...,z_N…...

【哈希表:哈希函数构造方法、哈希冲突的处理】
预测未来的最好方法就是创造它💦 目录 一、什么是Hash表 二、Hash冲突 三、Hash函数的构造方法 1. 直接定址法 2. 除余法 3. 基数转换法 4. 平方取中法 5. 折叠法 6. 移位法 7. 随机数法 四、处理冲突方法 1. 开放地址法 • 线性探测法 …...

HTML5 应用程序缓存
HTML5 应用程序缓存 使用 HTML5,通过创建 cache manifest 文件,可以轻松地创建 web 应用的离线版本。这意味着,你可以在没有网络连接的情况下进行访问。 什么是应用程序缓存(Application Cache)? HTML5 引…...

全国计算机等级考试三级网络技术选择题考点
目录 第一章 网络系统结构与设计的基本原则 第二章 中小型网络系统总体规划与设计方法 第三章 IP地址规划技术 第四章 路由设计基础 第五章 局域网技术基础应用 第六/七章 交换机/路由器及其配置 第八章 无线局域网技术 第九章 计算机网络信息服务系统的安装与…...

Python和VC代码实现希尔伯特变换(Hilbert transform)
文章目录前言一、希尔伯特变换是什么?二、VC中的实现原理及代码示例三、用Python代码实现总结前言 在数学和信号处理中,**希尔伯特变换(Hilbert transform)**是一个对函数产生定义域相同的函数的线性算子。 希尔伯特变换在信号处…...

嵌入式C语言语法概述
1.gcc概述 GCC全称是GUN C Compiler 随着时代的发展GCC支持的语言越来越多,它的名称变成了GNU Compiler Collection gcc的作用相当于翻译官,把程序设计语言翻译成计算机能理解的机器语言。 (1)gcc -o gcc -o (其…...
蓝桥杯第19天(Python)(疯狂刷题第3天)
题型: 1.思维题/杂题:数学公式,分析题意,找规律 2.BFS/DFS:广搜(递归实现),深搜(deque实现) 3.简单数论:模,素数(只需要…...
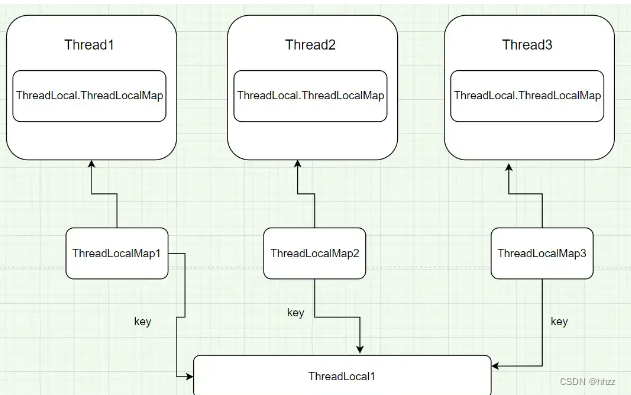
【数据库连接,线程,ThreadLocal三者之间的关系】
一、数据库连接与线程的关系 在实际项目中,数据库连接是很宝贵的资源,以MySQL为例,一台MySQL服务器最大连接数默认是100, 最大可以达到16384。但现实中最多是到200,再多MySQL服务器就承受不住了。因为mysql连接用的是tcp协议&…...
java 虚拟股票交易系统Myeclipse开发mysql数据库web结构jsp编程计算机网页项目
一、源码特点 JSP 虚拟股票交易系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统采用serlvetdaobean,系统具有完整的源代码和数据库,系统主要采用 B/S模式开发。 java 虚拟股票交易系统Myeclips…...

spring如何开启允许循环依赖
如何解决spring循环依赖 在Spring框架中,allowCircularReferences属性是用于控制Bean之间的循环依赖的。循环依赖是指两个或多个Bean之间相互依赖的情况,其中一个Bean依赖于另一个Bean,同时另一个Bean又依赖于第一个Bean。 allowCircularRe…...
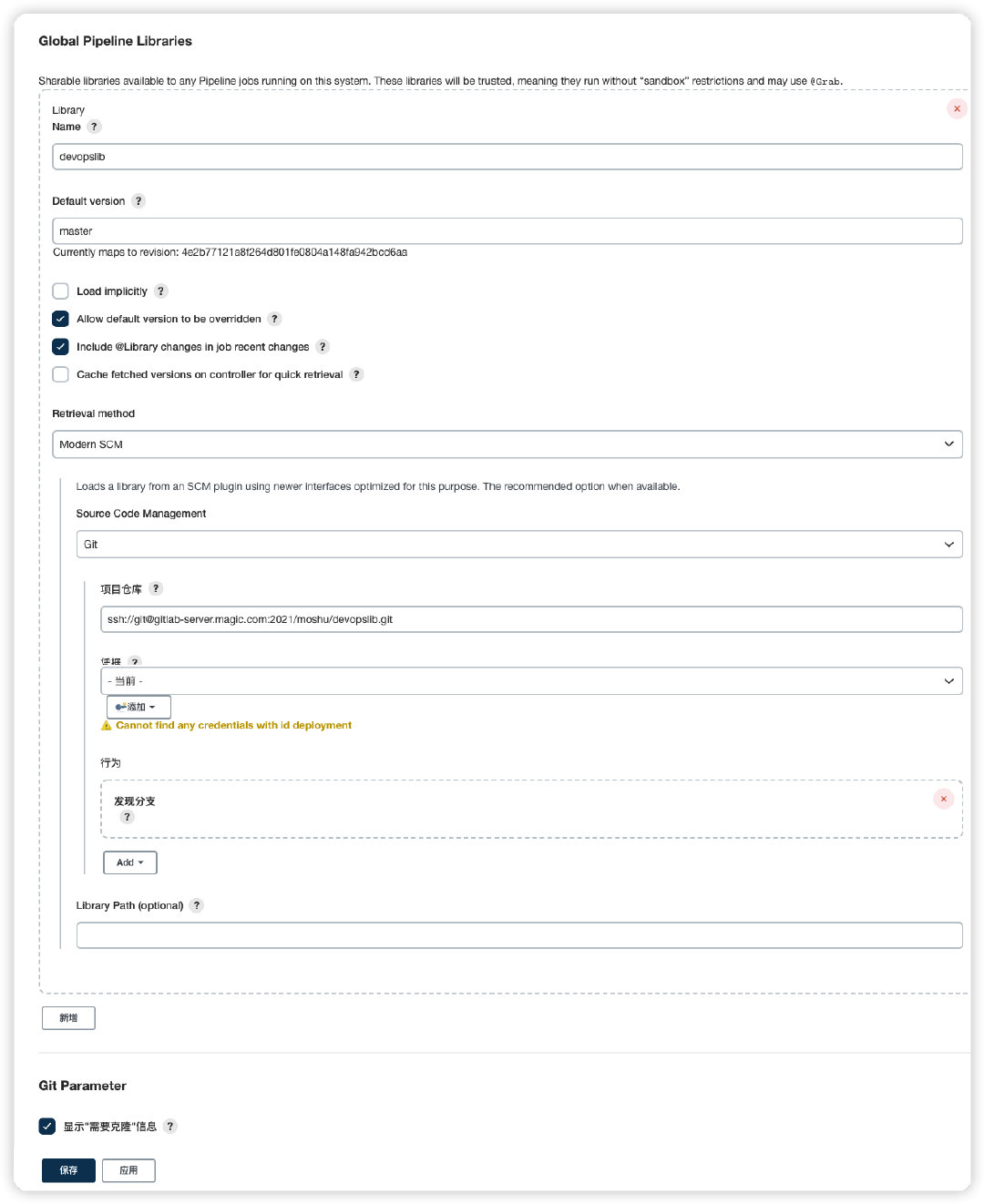
jenkins+sonarqube+自动部署服务
一、jenkins 配置Pipeline 二、新建共享库执行脚本 共享库可以是一个普通的gitlab项目,目录结构如下 三、添加到共享库 Jenkins Dashboard–>系统管理–>系统配置–>Global Pipeline Libraries Name: 共享库名称,自定义即可; Defa…...

【算法系列之动态规划III】背包问题
背包问题 01背包指的是物品只有1个,可以选也可以不选。完全背包是物品有无数个,可以选几个也可以不选。 二维数组01背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次&…...

MONAI-LayerFactory设计与实现
LayerFactory 用于创建图层的工厂对象,这使用给定的工厂函数来实际产生类型或构建可调用程序。这些函数是通过名称来参考的,可以在任何时候添加。 用到的关键技术点: 装饰器(Decorators), 例如:property装饰器,创建…...

Thinkphp 6.0路由的定义
本节课我们来了解一下路由方面的知识,然后简单的使用一下路由的功能。 一.路由简介 1. 路由的作用就是让 URL 地址更加的规范和优雅,或者说更加简洁; 2. 设置路由对 URL 的检测、验证等一系列操作提供了极大的便利性; …...

Kafka系列之:深入理解Kafka集群调优
Kafka系列之:深入理解Kafka集群调优 一、Kafka硬件配置选择二、Kafka内存选择三、CPU选择四、网络选择五、生产者调优六、broker调优七、消费者调优八、Kafka总体调优一、Kafka硬件配置选择 服务器台数选择: 2 * (生产者峰值生产速率 * 副本数 / 100) + 1磁盘选择: Kafka…...

creator-泄漏检测之资源篇
title: creator-泄漏检测之资源篇 categories: Cocos2dx tags: [creator, 优化, 泄漏, 内存] date: 2023-03-29 14:48:48 comments: false mathjax: true toc: true creator-泄漏检测之资源篇 前篇 资源释放 - https://docs.cocos.com/creator/manual/zh/asset/release-manager…...
)
【DevOps】Jenkins 运行任务时遇到 FATAL:Unable to produce a script file 报错(已解决)
文章目录一、问题描述二、定位原因三、解决方案四、其他方案五、总结关键词: Jenkins、Unable to produce a script file、UnmappableCharacterException、IOException: Failed to create a temp file on一、问题描述 由于使用的 Jenkins 存在安全漏洞(…...

Web前端
WEB前端 HTMLCSSJavaScriptjQuery(js框架)Bootstrap(CSS框架)AJAXJSON 文章目录 WEB前端WEB前端三大核心技术Web开发工具文本编辑器集成开发环境(IDE)浏览器选择HTML什么是 HTML?HTML版本变迁HTML-HelloWorldHTML 文档 = 网页HTML 标签属性(Attribute)HTML 常用标签...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
