选择很重要,骑友,怎么挑选骑行装备?
骑行装备的重要性,已经不用多说了,大家也都知道。但是如何挑选,如何选择适合自己的骑行装备呢?今天我来和大家聊一聊这个问题。
首先我们需要了解一个概念:骑行装备分为两大类:骑行服和骑行鞋。对于公路车来说,骑行服可以理解为“外套”,主要目的是为了保暖;而骑行鞋则是“鞋子”,主要作用是为了保护脚。
 另外还有一个概念也要知道:就是头盔,这个对于速度有一定要求的车手来说非常重要,因为在你在高速行驶的过程中,如果不戴头盔的话,头部很容易受到伤害。头盔对于车手来说是非常重要的存在,一定要选择适合自己的头盔。
另外还有一个概念也要知道:就是头盔,这个对于速度有一定要求的车手来说非常重要,因为在你在高速行驶的过程中,如果不戴头盔的话,头部很容易受到伤害。头盔对于车手来说是非常重要的存在,一定要选择适合自己的头盔。
好了,我们知道了骑行服和骑行鞋是为了保暖,那么对于公路车来说,又该如何挑选合适的骑行装备呢?主要是要看车手的身高、体重、腿长、手臂长度等各种数据,根据这些数据选择合适的骑行装备。
 1、身高
1、身高
身高是骑行装备中最重要的数据,也是很多车手都很在意的。很多车手都会关注自己的身高,毕竟穿上合适的装备,骑起来才会更加舒服。但是不能盲目的去追求高,因为我们要知道,我们并不是一天就能长大的。
在骑行时,需要根据自身的情况来选择合适自己的装备,不能一味地去追求高。身高和体重对于骑行装备来说是影响最大的两个数据。虽然身高也可以通过后期锻炼来改变,但是这个过程会非常漫长。所以如果你是一名新手车手,我建议你先从身高入手。
2、体重
对于大多数的公路车车手来说,他们的身高大约在170-180 cm之间,体重在70-75 kg之间,所以我们可以看到公路车的头盔一般都是根据体重来定制的。
对于那些身高较高、体重较大的车手来说,他们需要选择更大尺寸的头盔,以确保头部能够有足够的空间来容纳。
如果你是一位体重在80 kg左右的车手,那么你可能就需要选择一些比较小尺寸的头盔了,以确保头部不会受到过多的挤压。
通常情况下,这个尺寸要比你身高中最小的数字大一到两个码左右。
 3、腿长
3、腿长
腿长主要指的是车手的腿长,需要根据自己的腿长来选择合适的骑行装备。当然了,这个数据不能直接反映你腿的长度,所以最好是在专业人士的指导下进行测量。不过,如果你平时很少骑车,那就不用考虑腿长了。
在选择骑行装备时,要尽量选择大一号的骑行鞋和骑行服,这样会更舒服一些。
4、手臂长度
其实这个是非常重要的数据,很多人会忽略这个。其实对于大部分的车手来说,手臂长度都是一个“硬伤”,因为你的手臂长度是固定的,但是你的身高不同,所以这个数据也是不同的。
一般来讲,如果你身高较高,手臂比较长的话,那么选择一个短款的骑行服就可以了;而如果你身高不高,但是手臂比较长的话,那么你就需要选择一个长款的骑行服了。另外还需要注意一点:就是在买骑行服时不要买大了一码,不然会影响到你骑行时身体的稳定性。
 5、骑行服和骑行鞋的选择
5、骑行服和骑行鞋的选择
最后就是最重要的问题,如何选择适合自己的骑行服和骑行鞋?这一点其实和身高、体重、腿长、手臂长度等数据有关系,也是最重要的,因为你没有办法通过测量数据来确定自己的身体情况。但如果你在选装备方面有什么不明白的话,可以找专业人士来帮你选择,这也是一种方法。
相关文章:

选择很重要,骑友,怎么挑选骑行装备?
骑行装备的重要性,已经不用多说了,大家也都知道。但是如何挑选,如何选择适合自己的骑行装备呢?今天我来和大家聊一聊这个问题。首先我们需要了解一个概念:骑行装备分为两大类:骑行服和骑行鞋。对于公路车来…...

【JUC面试题】Java并发编程面试题
Java并发编程 基础知识 1. 为什么要使用并发编程? 提升多核系统的CPU利用率一般来说一台主机上的会有多个CPU核心,我们可以创建多个线程,理论 上讲操作系统可以将多个线程分配给不同的CPU去执行,每个CPU执行一个线程,…...

spark笔记
spark笔记 1. 概述 Spark是一种基于内存的快速、通用、可扩展的大数据分析计算引擎;Spark提供内存计算,将计算结果直接放在内存中,减少了迭代计算的IO开销,有更高效的运算效率。 1.1 Spark核心模块 Spark Core:提供S…...
丢失了packet.dll原因和解决方法全面指南
packet.dll是Windows操作系统中的一个重要文件,它主要用于网络通信,如果丢失了这个文件,可能会导致网络连接问题。本文将探讨packet.dll文件丢失的原因,并提供相应的解决方法。 一、丢失packet.dll文件的原因 1. 病毒感染&#x…...
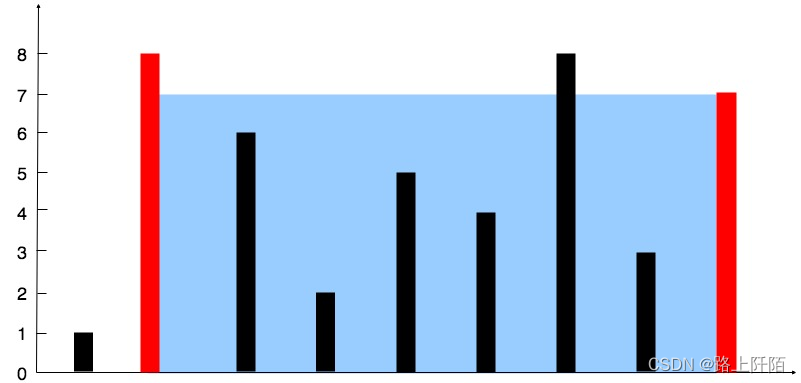
算法练习随记(三)
1.全排列 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示例 2: 输入&#x…...
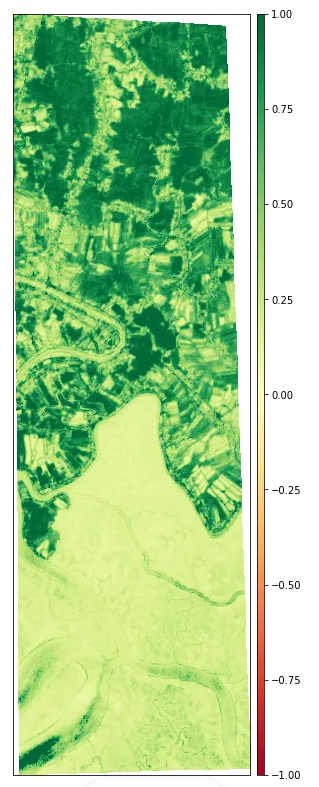
基于Python 进行卫星图像多种指数分析
一、前言本文帮助读者更好地了解卫星数据以及使用 Python 探索和分析哨兵2卫星数号数据在Sundarbans地区的不同方法。二、Sundarbans研究区孙德尔本斯(Sundarbans)是恒河、雅鲁藏布江和梅克纳河在孟加拉湾汇合形成的三角洲中最大的红树林区之一。 孙德尔…...
综合复习(C++,字符串,数学))
(Week 15)综合复习(C++,字符串,数学)
文章目录T1 [Daimayuan]删删(C,字符串)输入格式输出格式样例输入样例输出数据规模解题思路T2 [Daimayuan]快快变大(C,区间DP)输入格式输出格式样例输入样例输出数据规模解题思路T3 [Daimayuan]饿饿 饭饭2&a…...

迪赛智慧数——柱状图(正负条形图):“光棍”排行榜TOP10省份
效果图 中国单身男女最多的省份是广东,广东的人口是全国最多的。人口多了,单身的人也会多,单身女性324万,男性498万。全国第二的省份是四川省,单身女性256万,单身男性296万。 数据源:静态数据…...

IDEA集成chatGTP让你编码如虎添翼
第一步,打开您的IDEA, 打开首选项(Preference) -> 插件(Plugin) 在插件市场搜索 chatGPT, 点击安装 安装完毕后会提示您重启IDE, 重启IDEA. 重启后您会发现窗口,右边条上 竖着挂着个chatGPT按钮了。 第二步、配置APIkey或accessToken(二选一,推荐accessToken无费用…...
 方法、Python3 File readline() 方法)
Python3 os.close() 方法、Python3 File readline() 方法
Python3 os.close() 方法 概述 os.close() 方法用于关闭指定的文件描述符 fd。 语法 close()方法语法格式如下: os.close(fd);参数 fd -- 文件描述符。 返回值 该方法没有返回值。 实例 以下实例演示了 close() 方法的使用: #!/usr/bin/python3…...
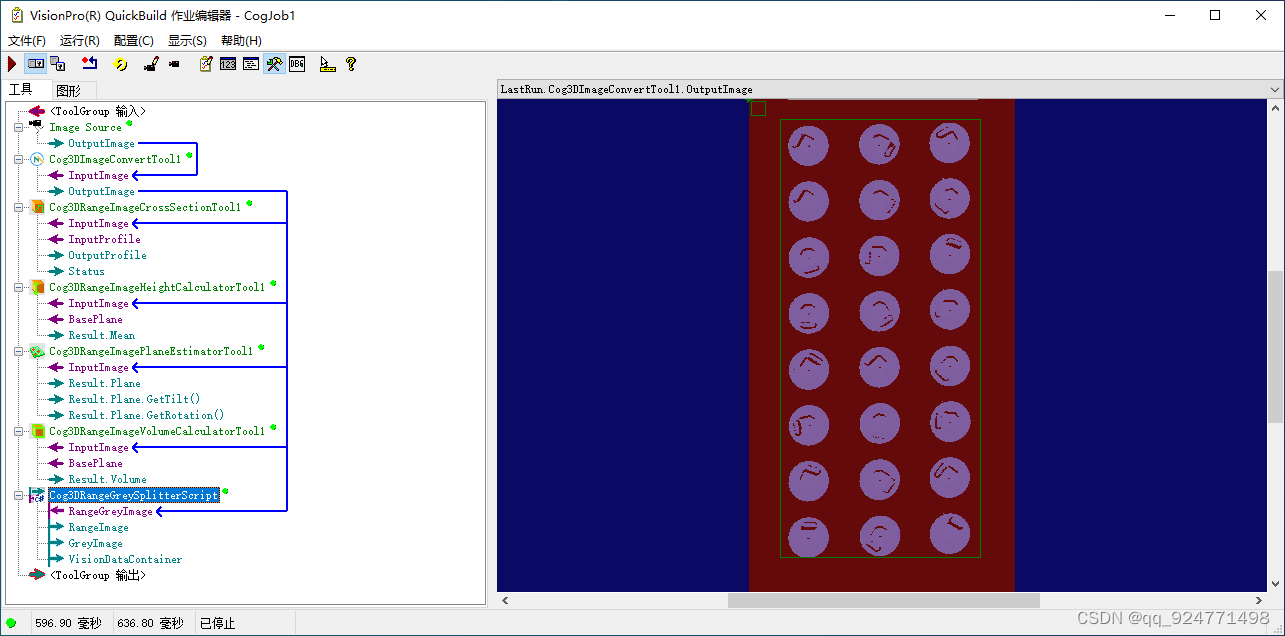
Vision Pro 自己写的一些自定义工具(c#)
目录前言一、保存图片工具1、展示2、源码下载地址二、3D图片格式转化1、展示2、源码下载地址三、所有工具汇总下载地址前言 自己用c#写的一些visionPro自定义工具,便于使用的时候直接拿出来,后续会不断添加新的工具。 想看怎么使用c#写visionPro自定义…...

ARM/FPGA/DSP板卡选型大全,总有一款适合您
创龙科技ARM/FPGA/DSP嵌入式板卡选型大全2023.2版本正式发布!接下来,跟着我们一起看看有哪些亮点吧! 6大主流工业处理器原厂 创龙科技现有30多条产品线,覆盖工业自动化、能源电力、仪器仪表、通信、医疗、安防等工业领域,与6大主流工业处理器原厂强强联合,包括德州仪器…...

【C语言蓝桥杯每日一题】—— 既约分数
【C语言蓝桥杯每日一题】—— 既约分数😎前言🙌既约分数🙌递归版解题代码:😍非递归版解题代码:😍总结撒花💞既约分数😎)😎博客昵称:博客小梦 &…...
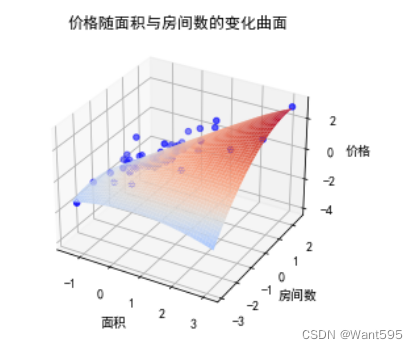
【机器学习】线性回归
文章目录前言一、单变量线性回归1.导入必要的库2.读取数据3.绘制散点图4.划分数据5.定义模型函数6.定义损失函数7.求权重向量w7.1 梯度下降函数7.2 最小二乘法8.训练模型9.绘制预测曲线10.试试正则化11.绘制预测曲线12.试试sklearn库二、多变量线性回归1.导入库2.读取数据3.划分…...

用ChatGPT学习多传感器融合中的基础知识
困惑与解答: 问题:匈牙利算法中的增广矩阵路径是什么意思 解答: 匈牙利算法是解决二分图最大匹配的经典算法之一。其中的增广矩阵路径指的是在当前匹配下,从一个未匹配节点开始,沿着交替路(交替路是指依次…...

PyCharm2020介绍
PyCharm2020PyCharm2020安装过程PyCharm2020安装包1、PyCharm2020介绍2、PyCharm2020特点3、PyCharm2020特点4、PyCharm2020PyCharm2020安装过程 PyCharm2020安装过程安装步骤点击此链接。 PyCharm2020安装包 链接:https://pan.baidu.com/s/19R3nJx6wMyNBU9oY4N4n…...
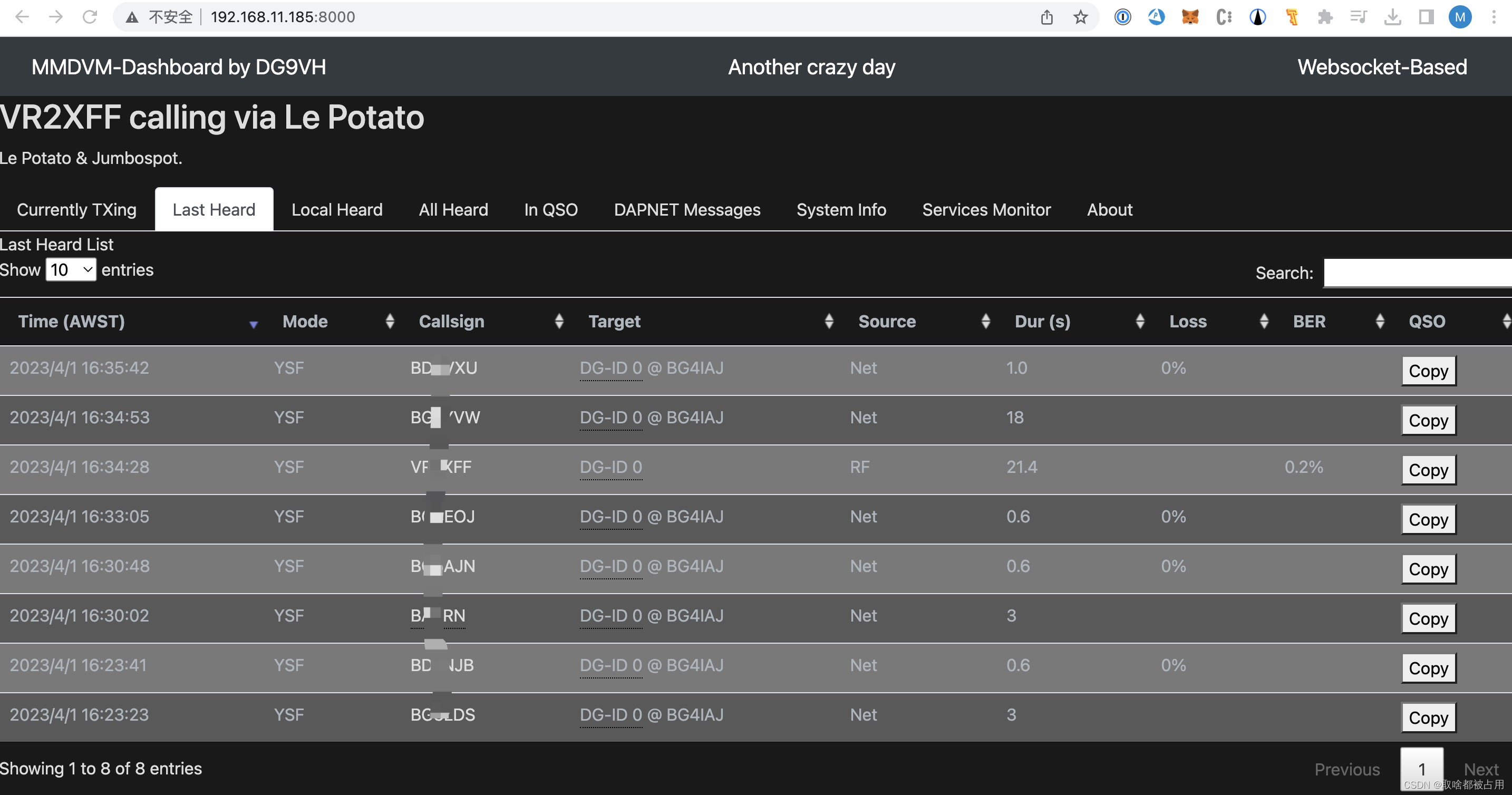
Le Potato + Jumbospot MMDVM热点盒子
最近才留意到,树莓派受到编程圈一定瞩目之后,智慧的同胞早已悄咪咪的搞了一堆xx派出来,本来对于香橙派,苹果派,土豆派和香蕉派是不感冒的,但是因为最近树莓派夸张的二级市场价格和断供,终于还是…...
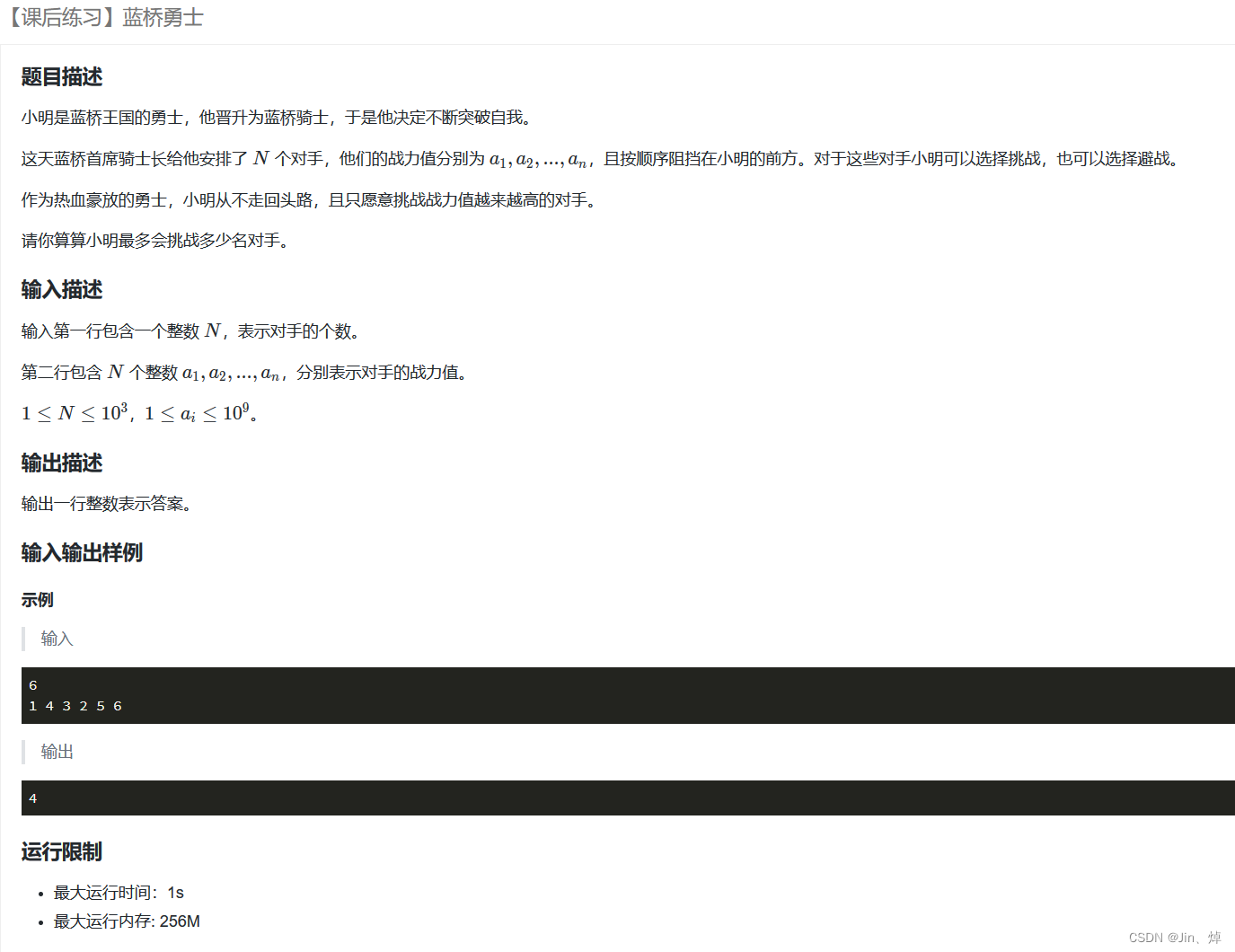
蓝桥杯第19天(Python)(疯狂刷题第2天)
题型: 1.思维题/杂题:数学公式,分析题意,找规律 2.BFS/DFS:广搜(递归实现),深搜(deque实现) 3.简单数论:模,素数(只需要…...
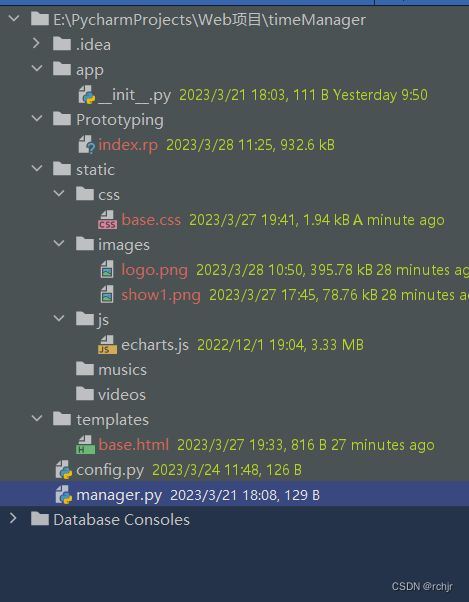
(五)手把手带你搭建精美简洁的个人时间管理网站—基于Axure的首页原型设计
🌟所属专栏:献给榕榕🐔作者简介:rchjr——五带信管菜只因一枚 😮前言:该专栏系为女友准备的,里面会不定时发一些讨好她的技术作品,感兴趣的小伙伴可以关注一下~👉文章简介…...

阿里面试:为什么MySQL不建议使用delete删除数据?
MySQL是一种关系型数据库管理系统,它的数据存储是基于磁盘上的文件系统实现的。MySQL将数据存储在表中,每个表由一系列的行和列组成。每一行表示一个记录,每一列表示一个字段。表的结构由其列名、数据类型、索引等信息组成。 MySQL的数据存储…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
