【机器学习】线性回归
文章目录
- 前言
- 一、单变量线性回归
- 1.导入必要的库
- 2.读取数据
- 3.绘制散点图
- 4.划分数据
- 5.定义模型函数
- 6.定义损失函数
- 7.求权重向量w
- 7.1 梯度下降函数
- 7.2 最小二乘法
- 8.训练模型
- 9.绘制预测曲线
- 10.试试正则化
- 11.绘制预测曲线
- 12.试试sklearn库
- 二、多变量线性回归
- 1.导入库
- 2.读取数据
- 3.划分数据
- 4.定义假设函数
- 5.定义损失函数
- 6.定义梯度下降函数
- 7.训练模型
- 8.运用sklearn绘图
- 总结
前言
线性回归:是一种通过属性的线性组合来进行预测的线性模型
其目的是找到一条直线或者一个平面或者更高维的超平面,使得预测值与真实值之间的误差最小化。
一、单变量线性回归
1.导入必要的库
导入pandas、numpy和matplotlib.pyplot库
import pandas as pd #导入pandas库
import numpy as np #导入numpy库
import matplotlib.pyplot as plt #导入matplotlib.pyplot库
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
2.读取数据
使用pandas库的read_csv()函数读取数据文件,数据文件中包含了人口和收益两列数据
data=pd.read_csv(r"d:线性回归/regress_data1.csv") #读取数据
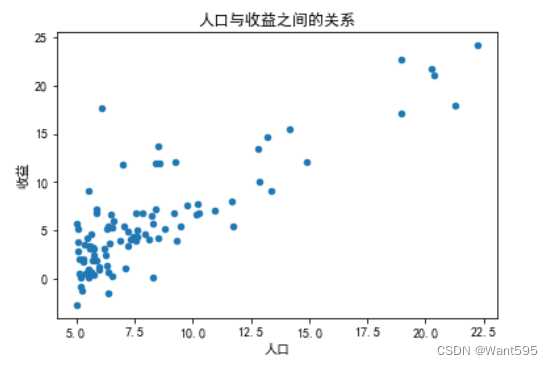
3.绘制散点图
使用data.plot()函数绘制散点图,展示人口与收益之间的关系
data.plot(kind="scatter",x="人口",y="收益") #绘制散点图
plt.xlabel("人口",fontsize=10) #横坐标
plt.ylabel("收益",fontsize=10) #纵坐标
plt.title("人口与收益之间的关系") #标题
plt.show() #画图
4.划分数据
这里是为了方便后面计算,将一列全为1的列插入到数据中
将数据分为训练集和测试集,这里只使用了训练集
data.insert(0,"ones",1) #插入列,便于后面计算
col_num=data.shape[1] #训练特征个数
m=data.shape[0] #训练标签个数
X=data.iloc[:,:col_num-1].values #训练集的特征
y=data.iloc[:,col_num-1].values #训练集的标签
y=y.reshape((m,1))
5.定义模型函数
定义h(X,w)函数用来计算模型预测值,这里采用的是线性模型
def h(X,w):return X@w
6.定义损失函数
定义cost(X,y,w)函数用来计算模型误差
def cost(X,y,w):return np.sum(np.power(h(X,w)-y,2))/(2*m)
7.求权重向量w
7.1 梯度下降函数
定义函数gradient_descent(X,y,w,n,a)用来执行梯度下降算法,更新权重向量w,并返回最终的权重向量和误差列表
def gradient_descent(X,y,w,n,a):t=wcost_lst=[]for i in range(n):error=h(X,w)-yfor j in range(col_num-1):t[j][0]=w[j][0]-((a/m)*np.sum(error.ravel()*X[:,j].ravel()))w=tcost_lst.append(cost(X,y,w))return w,cost_lst
7.2 最小二乘法
定义函数least_square(X,y)用来执行最小二乘法,直接求出权重向量w,但是当n>10000时由于时间复杂度太大将导致程序运行超时
def least_square(X,y):w=np.linalg.inv(X.T@X)@X.T@yreturn w
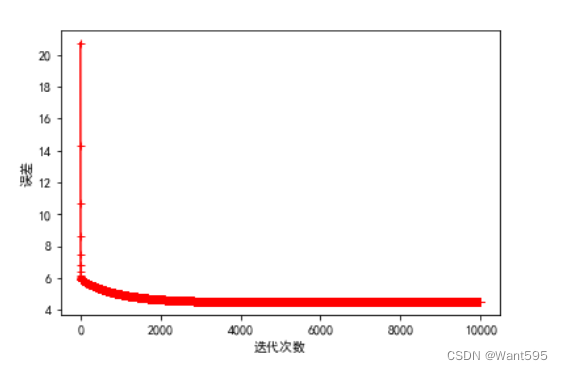
8.训练模型
调用gradient_descent()函数训练模型,并输出误差随迭代次数变化的图像,用来观察模型的学习效果
其中,迭代次数越大,训练效果越好,学习率适中,既不可太大,也不可过小
n=10000 #迭代次数越多越好
a=0.003 #学习率适中,不能太大,也不能太小
w=np.zeros((col_num-1,1)) #初始化权重向量
w,cost_lst=gradient_descent(X,y,w,n,a) #调用梯度下降函数
plt.plot(range(n),cost_lst,"r-+")
plt.xlabel("迭代次数")
plt.ylabel("误差")
plt.show()
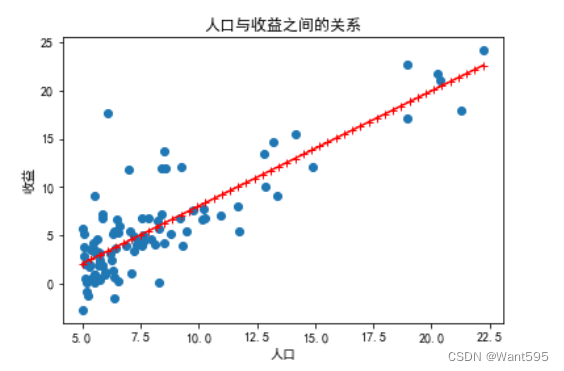
9.绘制预测曲线
使用训练好的权重向量w绘制预测曲线,并将其与原始数据一起绘制在图像上,用来观察模型的预测效果
x=np.linspace(data["人口"].min(),data["人口"].max(),50) #预测特征
y1=w[0,0]*1+w[1,0]*x #预测标签
plt.scatter(data["人口"],data["收益"], label='训练数据') #训练集
plt.plot(x,y1,"r-+",label="预测线") #预测集
plt.xlabel("人口",fontsize=10)
plt.ylabel("收益",fontsize=10)
plt.title("人口与收益之间的关系")
plt.show()
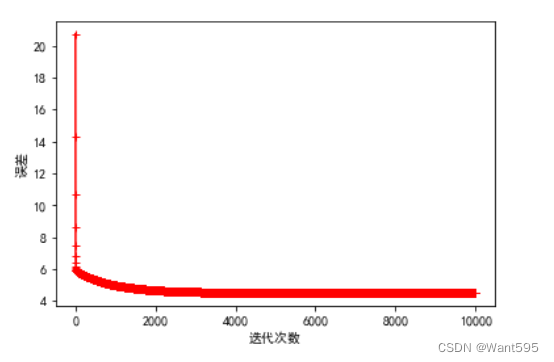
10.试试正则化
使用L2正则化(岭回归)防止过拟合
def gradient_descents(X,y,w,n,a,l):t=wcost_lst=[]for i in range(n):error=h(X,w)-yfor j in range(col_num-1):t[j][0]=w[j][0]-((a/m)*(np.sum(error.ravel()*X[:,j].ravel())+2*l*w[j,0]))w=tcost_lst.append(cost(X,y,w))return w,cost_lst
n=10000 #迭代次数越多越好
a=0.003 #学习率适中,不能太大,也不能太小
l=1 #λ
w=np.zeros((col_num-1,1))
w,cost_lst=gradient_descents(X,y,w,n,a,l)
plt.plot(range(n),cost_lst,"r-+")
plt.xlabel("迭代次数")
plt.ylabel("误差")
plt.show()
11.绘制预测曲线
使用训练好的权重向量w绘制预测曲线,并将其与原始数据一起绘制在图像上,用来观察模型的预测效果
x=np.linspace(data["人口"].min(),data["人口"].max(),50)
y1=w[0,0]*1+w[1,0]*x
plt.scatter(data["人口"],data["收益"], label='训练数据')
plt.plot(x,y1,"r-+",label="预测线")
plt.xlabel("人口",fontsize=10)
plt.ylabel("收益",fontsize=10)
plt.title("人口与收益之间的关系")
plt.show()
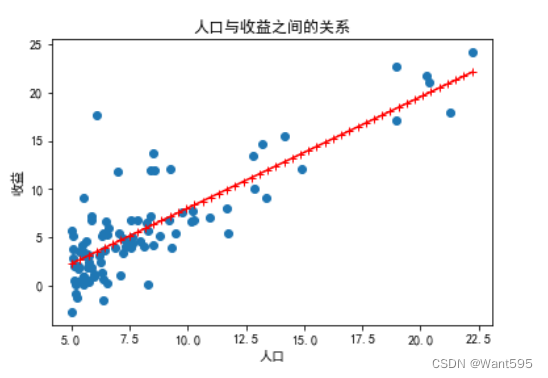
12.试试sklearn库
import pandas as pd #导入pandas库
import numpy as np #导入numpy库
import matplotlib.pyplot as plt #导入matplotlib.pyplot库
import sklearn #导入sklearn库
from sklearn import linear_model
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
# 2.读取数据:使用pandas库的read_csv()函数读取数据文件。数据文件中包含了人口和收益两列数据。
data=pd.read_csv(r"d:线性回归/regress_data1.csv") #读取数据
data.insert(0,"ones",1) #插入列
col_num=data.shape[1] #列数
m=data.shape[0] #行数
# 5.划分数据:将数据分为训练集和测试集,这里只使用了训练集。
X=data.iloc[:,:col_num-1].values #训练集的特征
y=data.iloc[:,col_num-1].values #训练集的标签
y.reshape((m,1))
mod=linear_model.LinearRegression()
mod.fit(X,y)
Y=mod.predict(X)
plt.scatter(X[:,1],y,marker='o',color='b')
plt.plot(X,Y,marker='+',color='r')
plt.xlabel("人口")
plt.ylabel("收益")
plt.show()
二、多变量线性回归
1.导入库
import pandas as pd #导入pandas库
import numpy as np #导入numpy库
import matplotlib.pyplot as plt #导入matplotlib.pyplot库
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
2.读取数据
datas=pd.read_csv(r"d:/线性回归/regress_data2.csv") #读取数据
datas=(datas-datas.mean())/datas.std() #正则化
3.划分数据
datas.insert(0,'ones',1) #插入列
col_num=datas.shape[1] #训练特征个数
m=datas.shape[0] #训练标签
X=datas.iloc[:,:col_num-1].values #训练特征
y=datas.iloc[:,col_num-1].values #训练标签
y=y.reshape((m,1))
4.定义假设函数
def h(X,w):return X@w
5.定义损失函数
def cost(X,y,w):return np.sum(np.power(h(X,w)-y,2))/(2*m)
6.定义梯度下降函数
def gradient_descent(X,y,w,n,a):t=wcost_lst=[]for i in range(n):error=h(X,w)-yfor j in range(col_num-1):t[j,0]=w[j,0]-((a/m)*np.sum(error.ravel()*X[:,j].ravel()))w=tcost_lst.append(cost(X,y,w))return w,cost_lst
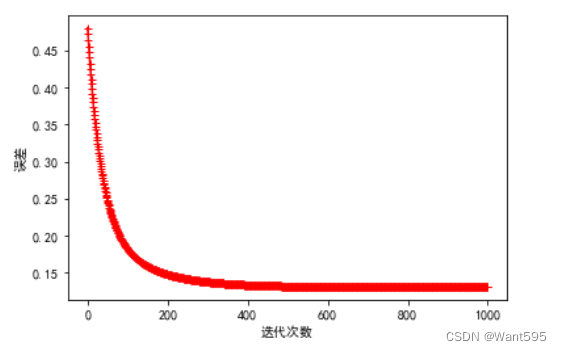
7.训练模型
n=1000 #迭代次数
a=0.01 #学习率
w=np.zeros((col_num-1,1)) #初始化特征向量w
w,cost_lst=gradient_descent(X,y,w,n,a)
plt.plot(range(n),cost_lst,'r+-')
plt.xlabel("迭代次数")
plt.ylabel("误差")
plt.show()
8.运用sklearn绘图
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取数据
datas = pd.read_csv(r"d:线性回归/regress_data2.csv")
datas = (datas - datas.mean()) / datas.std()
X = datas.iloc[:, :-1].values
y = datas.iloc[:, -1].values.reshape(-1, 1)
# 多项式回归
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
mod = linear_model.LinearRegression()
mod.fit(X_poly, y)
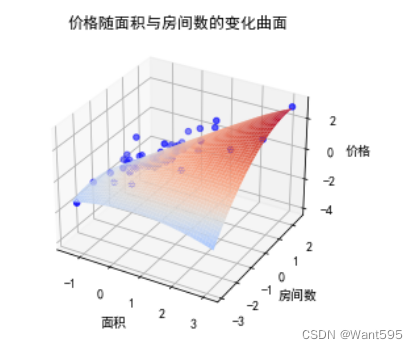
# 绘制拟合曲线
x1 = np.linspace(datas["面积"].min(), datas["面积"].max(), 50)
x2 = np.linspace(datas["房间数"].min(), datas["房间数"].max(), 50)
x1, x2 = np.meshgrid(x1, x2)
X_grid = np.column_stack((x1.flatten(), x2.flatten()))
X_grid_poly = poly.fit_transform(X_grid)
y_pred = mod.predict(X_grid_poly)
fig=plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(X[:,0], X[:,1], y, marker='o', color='b')
ax.plot_surface(x1, x2, y_pred.reshape(x1.shape), cmap='coolwarm')
ax.set_title("价格随面积与房间数的变化曲面")
ax.set_xlabel("面积")
ax.set_ylabel("房间数")
ax.set_zlabel("价格")
plt.show()
总结
线性回归三大要素
- 假设函数 h(X,w)
- 损失函数 cost(X,y,w)
- 梯度下降/最小二乘函数(求解权重向量w的函数)
普通线性回归步骤
- 导入库
- 读取数据
- 划分数据
- 假设函数(模型函数)
- 损失函数
- 梯度下降/最小二乘
- 训练模型
- 绘图预测
调用sklearn库进行线性回归的步骤
- 导入库
- 读取数据
- 调用sklearn库
- 绘图
相关文章:

【机器学习】线性回归
文章目录前言一、单变量线性回归1.导入必要的库2.读取数据3.绘制散点图4.划分数据5.定义模型函数6.定义损失函数7.求权重向量w7.1 梯度下降函数7.2 最小二乘法8.训练模型9.绘制预测曲线10.试试正则化11.绘制预测曲线12.试试sklearn库二、多变量线性回归1.导入库2.读取数据3.划分…...

用ChatGPT学习多传感器融合中的基础知识
困惑与解答: 问题:匈牙利算法中的增广矩阵路径是什么意思 解答: 匈牙利算法是解决二分图最大匹配的经典算法之一。其中的增广矩阵路径指的是在当前匹配下,从一个未匹配节点开始,沿着交替路(交替路是指依次…...

PyCharm2020介绍
PyCharm2020PyCharm2020安装过程PyCharm2020安装包1、PyCharm2020介绍2、PyCharm2020特点3、PyCharm2020特点4、PyCharm2020PyCharm2020安装过程 PyCharm2020安装过程安装步骤点击此链接。 PyCharm2020安装包 链接:https://pan.baidu.com/s/19R3nJx6wMyNBU9oY4N4n…...
Le Potato + Jumbospot MMDVM热点盒子
最近才留意到,树莓派受到编程圈一定瞩目之后,智慧的同胞早已悄咪咪的搞了一堆xx派出来,本来对于香橙派,苹果派,土豆派和香蕉派是不感冒的,但是因为最近树莓派夸张的二级市场价格和断供,终于还是…...
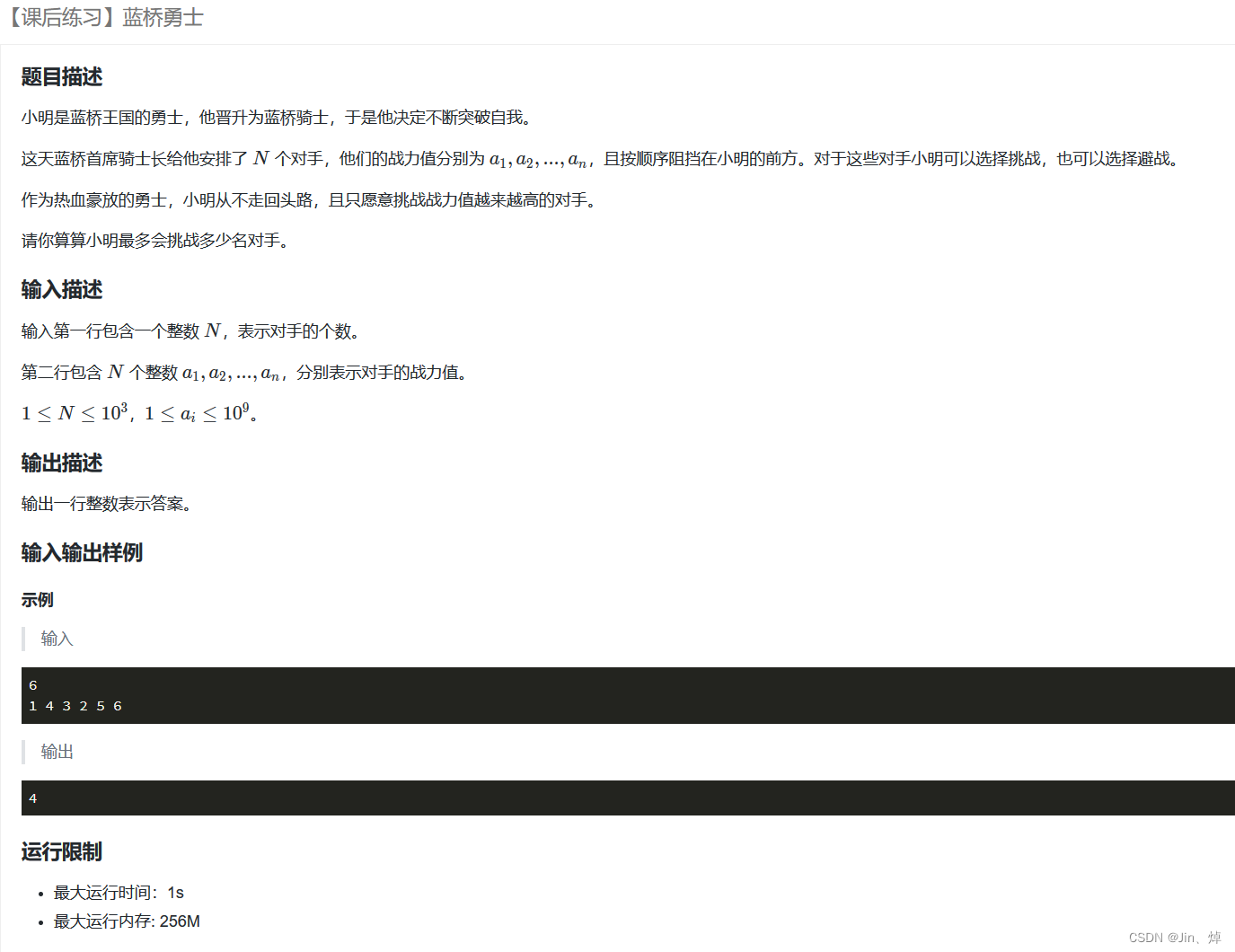
蓝桥杯第19天(Python)(疯狂刷题第2天)
题型: 1.思维题/杂题:数学公式,分析题意,找规律 2.BFS/DFS:广搜(递归实现),深搜(deque实现) 3.简单数论:模,素数(只需要…...
(五)手把手带你搭建精美简洁的个人时间管理网站—基于Axure的首页原型设计
🌟所属专栏:献给榕榕🐔作者简介:rchjr——五带信管菜只因一枚 😮前言:该专栏系为女友准备的,里面会不定时发一些讨好她的技术作品,感兴趣的小伙伴可以关注一下~👉文章简介…...

阿里面试:为什么MySQL不建议使用delete删除数据?
MySQL是一种关系型数据库管理系统,它的数据存储是基于磁盘上的文件系统实现的。MySQL将数据存储在表中,每个表由一系列的行和列组成。每一行表示一个记录,每一列表示一个字段。表的结构由其列名、数据类型、索引等信息组成。 MySQL的数据存储…...

低代码开发公司:用科技强力开启产业分工新时代!
实现办公自动化,是不少企业的共同追求。低代码开发公司会遵循时代发展规律,注入强劲的科技新生力量,在低代码开发市场厚积爆发、努力奋斗,推动企业数字化转型升级,为每一个企业的办公自动化升级创新贡献应有的力量。 一…...
)
参考mfa官方文档实践笔记(亲测)
按顺序执行以下指令: conda create -n aligner -c conda-forge montreal-forced-alignerconda config --add channels conda-forgeconda activate alignerconda install pytorch torchvision torchaudio pytorch-cuda11.7 -c pytorch -c nvidia 如果报错࿱…...

【 第六章 拦截器,注解配置springMVC,springMVC执行流程】
第六章 拦截器,注解配置springMVC,springMVC执行流程 1.拦截器: ①springMVC中的拦截器用于拦截控制器方法的执行。 ②springMVC的拦截器需要实现HandlerInterceptor或者继承HandlerInterceptorAdapter类。 ③springMVC的拦截器必须在spring…...
一种编译器视角下的python性能优化
“Life is short,You need python”!老码农很喜欢python的优雅,然而,在生产环境中,Python这样的没有优先考虑性能构建优化的动态语言特性可能是危险的,因此,流行的高性能库如TensorFlow 或PyTor…...

太逼真!这个韩国虚拟女团你追不追?
“她们看上去太像真人了”, 韩国虚拟女团MAVE的首支MV和打歌舞台引发网友阵阵惊呼。现在,她们的舞蹈已经有真人在挑战了。 这一组虚拟人的“逼真”倒不在脸,主要是MAVE女团的舞台动作接近自然,不放近景看,基本可以达到…...

安全与道路测试:自动驾驶系统安全性探究
随着自动驾驶技术的迅速发展,如何确保自动驾驶系统的安全性已成为业界关注的焦点。本文将探讨自动驾驶系统的潜在风险、安全设计原则和道路测试要求。 潜在风险 自动驾驶系统在改善交通安全和提高出行效率方面具有巨大潜力,但其安全性仍面临许多挑战&a…...

chatGPT学英语,真香!!!
文章目录学习目标学习内容目标方式过程学习时间学习产出学习目标 能够在三个月的练习后,和真人外教比较流畅的沟通! 最近chatGPT实在是太火了,各种事情都能干,能改论文、写代码和翻译。 看到B站很多教程教我们直接用chatGPT进行…...

12 Cache Memory
内存的层次结构 计算机内存的层级结构是一种将不同类型的存储设备按照速度、容量和访问时间组织起来的方式。这种层级结构提高了计算机的性能,使得处理器能够高效地访问数据。通常,内存层级结构可分为以下几个层次: 寄存器:寄存器…...

【CSS系列】第一章 · CSS基础
写在前面 Hello大家好, 我是【麟-小白】,一位软件工程专业的学生,喜好计算机知识。希望大家能够一起学习进步呀!本人是一名在读大学生,专业水平有限,如发现错误或不足之处,请多多指正࿰…...

【Java代码审计】表达式注入
1 前置知识 1.1 EL表达式 EL表达式主要功能: 获取数据:可以从JSP四大作用域中获取数据执行运算:执行一些关系运算,逻辑运算,算术运算获取web开发常用对象:通过内置 的11个隐式对象获取想要的数据调用jav…...
Python-GEE遥感云大数据分析、管理与可视化
Python-GEE遥感云大数据分析、管理与可视化近年来遥感技术得到了突飞猛进的发展,航天、航空、临近空间等多遥感平台不断增加,数据的空间、时间、光谱分辨率不断提高,数据量猛增,遥感数据已经越来越具有大数据特征。遥感大数据的出…...
 | 洛谷 P2731 [USACO3.3]骑马修栅栏 Riding the Fences)
信息学奥赛一本通 1375:骑马修栅栏(fence) | 洛谷 P2731 [USACO3.3]骑马修栅栏 Riding the Fences
【题目链接】 ybt 1375:骑马修栅栏(fence) 洛谷 P2731 [USACO3.3]骑马修栅栏 Riding the Fences 【题目考点】 1. 图论:欧拉回路 欧拉回路存在的条件:图中所有顶点的度都是偶数欧拉路径存在的条件:图中只有两个度为奇数的顶点…...
Spring Boot 应用的打包和发布
1. 创建项目(example-fast) 基于 Spring Boot 创建一个 WEB 项目 example-fast。 2. 编译打包 2.1 采用 IDEA 集成的 Maven 环境来对 Spring Boot 项目编译打包,可谓是超级 easy 2.2 mvn 命令打包 # mvn clean 清理编译 # install 打包 #…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
