DAY17||654.最大二叉树 |617.合并二叉树 |700.二叉搜索树中的搜索 |

654.最大二叉树

题目：654. 最大二叉树 - 力扣（LeetCode）

给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：

• 二叉树的根是数组中的最大元素。
• 左子树是通过数组中最大值左边部分构造出的最大二叉树。
• 右子树是通过数组中最大值右边部分构造出的最大二叉树。

通过给定的数组构建最大二叉树，并且输出这个树的根节点。

示例 ：

构造二叉树一定要前序遍历，因为要先找到中，才能分割左右子树。

本题图解思路：

 

 

class Solution {
public:TreeNode* constructMaximumBinaryTree(vector<int>& nums) {TreeNode*node=new TreeNode(0);//如果数组只有一个元素的情况if(nums.size()==1){node->val=nums[0];return node;}//找到中int maxValue=0;int maxValueIndex=0;for(int i=0;i<nums.size();i++){if(nums[i]>maxValue){maxValueIndex=i;maxValue=nums[i];}}node->val=maxValue;//分割左右子树//递归构建左子树，新建一个数组if(maxValueIndex>0)//保证数组元素大于1,如果不写if的话就要另开一个函数，空的情况返回{vector<int>leftvec(nums.begin(),nums.begin()+maxValueIndex);//左开右闭写法node->left=constructMaximumBinaryTree(leftvec);}//递归构建右子树if(maxValueIndex<nums.size()-1){vector<int>rightvec(nums.begin()+maxValueIndex+1,nums.end());node->right=constructMaximumBinaryTree(rightvec);}return node;}
};

本题做过上一题构建数组确实变得容易很多。代码优化方向有，不用每次找左右子树的时候构建新的数组的话效率就会高很多。（即直接用下标索引直接在原数组上操作）

关于加不加if的问题，如果允许空节点进入递归，就不加。

617.合并二叉树

题目：617. 合并二叉树 - 力扣（LeetCode）

 

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例 1:

注意: 合并必须从两个树的根节点开始

哪种遍历方式都可以。其实就是同时遍历两颗二叉树，相同位置上的元素合并，如果一方有一方没有的情况，就把2的节点加到1中去就可以了。

前序遍历例子：

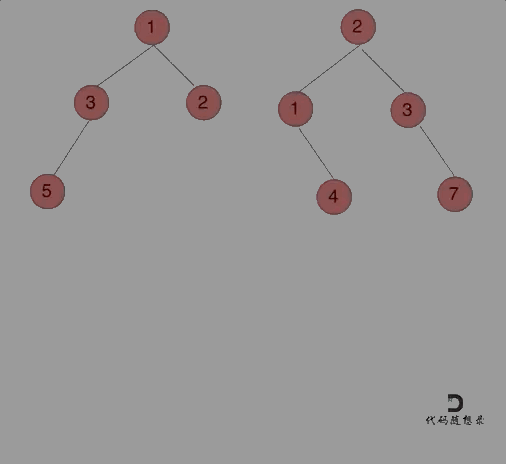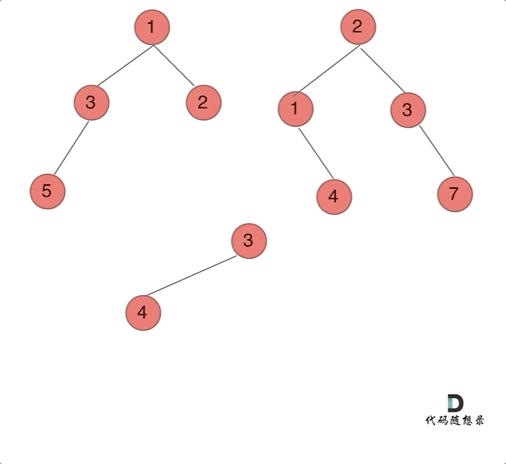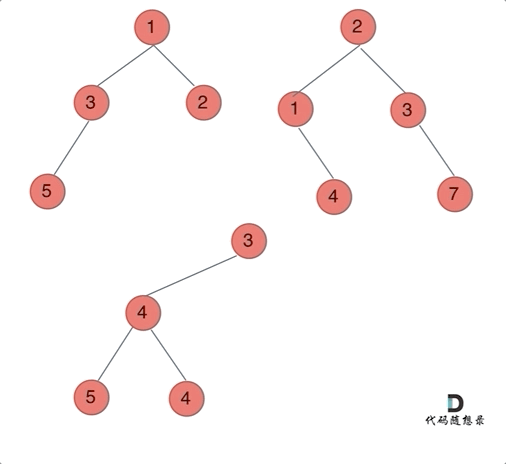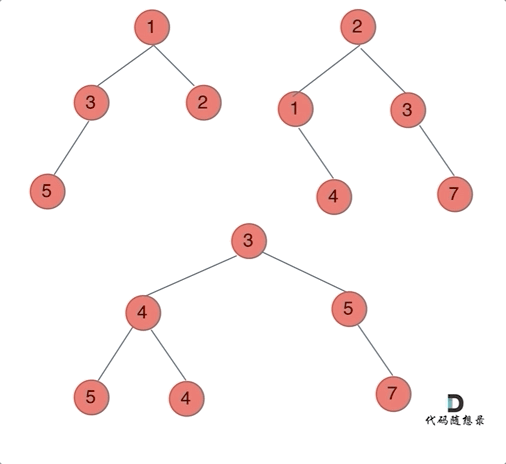
前中后序的区别只是左中右的顺序调换而已。

前序遍历（递归） 

class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if(root1==NULL)return root2;//如果t1为空，返回t2的值。如果两个都为空，那么其实返回的就是NULL了if(root2==NULL)return root1;root1->val+=root2->val;//合并root1->left=mergeTrees(root1->left,root2->left);root1->right=mergeTrees(root1->right,root2->right);return root1;}
};

迭代法（层序遍历） 

使用队列来其实这个写法最好理解思路。

同时遍历，入队列。

需要注意的是节点的左右子树入列的时候，当左子树不为空，右子树为空的情况其实已经被左子树的值加上右子树的值 处理过了

class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if(root1==NULL)return root2;if(root2==NULL)return root1;queue<TreeNode*>que;//一定都不为空入列que.push(root1);que.push(root2);while(!que.empty()){TreeNode*node1=que.front();que.pop();TreeNode*node2=que.front();que.pop();node1->val+=node2->val;//合并步骤if(node1->left&&node2->left)//两棵树的左子树都在，入列{que.push(node1->left);que.push(node2->left);}if(node1->right&&node2->right)//两棵树的右子树都在，入列{que.push(node1->right);que.push(node2->right);}if(!node1->left&&node2->left)//如果1的左空，2的不空，就把2的赋值过去{node1->left=node2->left;}if(!node1->right&&node2->right)//如果1的左空，2的不空，就把2的赋值过去{node1->right=node2->right;}}return root1;//这里返回的是root1而不是node1的原因是，node1只是一个指针，它操作的对象是入了队列的root数}
};

其实，定义的node1和node2是一个指针，它指向指针root1和root2.

700.二叉搜索树中的搜索

题目700. 二叉搜索树中的搜索 - 力扣（LeetCode） 

给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。

例如，

在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。

 

二叉搜索树是一个有序树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉搜索树

因为二叉搜索树的节点是有序的，所以可以有方向的去搜索。

如果root->val > val，搜索左子树，如果root->val < val，就搜索右子树，最后如果都没有搜索到，就返回NULL。

递归法

class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if(root==NULL||root->val==val)return root;//如果为空或者找到了值，就返回//找左子树if(root->val>val)return searchBST(root->left,val);//找右子树if(root->val<val)return searchBST(root->right,val);return NULL;}
};

迭代法

对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。

而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。

class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {while(root){if(root->val>val)root=root->left;else if(root->val<val)root=root->right;else return root;}return NULL;}
};

 本题真的非常简单。因为二叉搜索树的有序性，所以不需要回溯写法。

98.验证二叉搜索树

题目：98. 验证二叉搜索树 - 力扣（LeetCode）

本题看似简单，陷阱挺多的。

我们要比较的是 左子树所有节点小于中间节点，右子树所有节点大于中间节点。

递归法

1.可以中序遍历，把所有节点元素放入一个数组，然后在逐个比较数组是否是递增的。（个人觉得好理解）

class Solution {private:vector<int>vec;void traversal(TreeNode*root){if(root==NULL)return;if(root->left)traversal(root->left);vec.push_back(root->val);if(root->right)traversal(root->right);}
public:bool isValidBST(TreeNode* root) {vec.clear();traversal(root);for(int i=1;i<vec.size();i++){if(vec[i]<=vec[i-1])return false;}return true;}
};

2.当然也可以直接在递归遍历时比较节点大小

只有寻找某一条边（或者一个节点）的时候，递归函数会有bool类型的返回值。

其实本题是同样的道理，我们在寻找一个不符合条件的节点，如果没有找到这个节点就遍历了整个树，如果找到不符合的节点了，立刻返回。

class Solution {
public:long long maxVal = LONG_MIN; // 因为后台测试数据中有int最小值bool isValidBST(TreeNode* root) {if(root==NULL)return true;//空二叉树（即没有任何节点的二叉树）被认为是一个有效的二叉搜索树（BST）。bool right=isValidBST(root->left);//左//中。遍历整棵树，其实如果遇到不是递增的情况就返回false了。if(maxVal<root->val)maxVal=root->val;else return false;bool left=isValidBST(root->right);//右，不需要加if条件判断节点是否为空，因为空节点直接返回truereturn left&&right;}
};

maxVal 是一个用于记录当前遍历到的节点值的变量。初始化为 LONG_MIN 是为了确保无论二叉树的节点值多小，它们最初都比这个值大。这是因为二叉搜索树的性质要求，左子树中的所有节点值都小于根节点值。

最终返回值是左子树（right）和右子树（left）验证结果的 逻辑与（&&），只有当左右子树都为 BST 时，整棵树才是 BST。

迭代法 

使用栈模拟中序遍历。其实就是双指针法的。一个指针指向树节点，另一个指针指向NULL。当中序遍历走的过程，两指针同步移动，pre一定指向cur的上一个指向的节点。（好理解）

class Solution {
public:bool isValidBST(TreeNode* root) {stack<TreeNode*>st;TreeNode*cur=root;TreeNode*pre=NULL;while(cur!=NULL||!st.empty()){if(cur!=NULL){st.push(cur);cur=cur->left;//左子树入栈，按栈的存储结构和中序遍历特性，只要左树一直不为空，就入栈，反正出栈顺序就是中序遍历的顺序！}else//如果当前节点为空但栈不为空，就遍历右子树，并且比较是否符合二叉搜索树特性{cur=st.top();//中st.pop();//出栈if(pre!=NULL&&cur->val<=pre->val)return false;//错误情况pre=cur;//保存上一个数cur=cur->right;//右}}return true;  }
};