Unity3D 创建一个人物,实现人物的移动
1,创建项目
首先打开我们的Unity Hub

在我们的编译器下面新建项目,选择3D模板,更改一下我们的项目名称,选择一下路径,然后点击创建项目

等待项目创建。。。。。。

我们在项目里先创建一个plane,这样有点视觉体验

点击Wnidows --> Asset Store。搜索:Character Pack: Free Sample
点击添加至我的资源,在Unity中打开
回到我们的Unity就会弹出一个模态框,点击import
(因为我之前就已经下载过这个,你们应该会有一个DownLoad,点击下载即可,如果下载出现问题就重新再下载一遍就好了)

点击import

我们就可以看到我们Assets里面就出现我们下载的包

跟随我的目录找到人物模型
![]()
我们将人物拖拽到Scene界面即可

开始添加人物动画
在Assets界面右键鼠标,选择Create,选择Animation,更改一下名字为Move
将创建好的动画控制器Animation,添加到我们人物上面
点击状态机界面,就会有我们刚才创建的了

在Assets界面右键鼠标,选择Create,选择C# Script,我们将这个代码名字命名为Move

点击刚刚创建好的人物,把我们创建好的C#代码拖拽进去

跟随我的目录,找到资源动画
![]()
这个Idle就是人物待机动画,这个Run就是我们人物跑起来时的动画

我们将Idle 和 Run拖拽到我们的状态机里面,把我们刚才的Move删除,右键 idle,选择Make Transition,连接到我们的run,同理右键run,连接到idle

选择一下我们要配置的参数,选择bool类型,更改一下名字为isRun

点击我们idle到run的小箭头,改成我这个样子(从idle到run是true)

同理点击run到idle的箭头,更改一下属性(从run到idle是false)

点击动画控制器,将控制器拖拽到Controller上面


双击我们创建好的C#代码,将这串代码复制上去。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;public class CharacterControl : MonoBehaviour
{private CharacterControl _character;private Animator animator;// Start is called before the first frame updatevoid Start(){_character = GetComponent<CharacterControl>();animator = GetComponent<Animator>();}// Update is called once per framevoid Update(){float horizontal = Input.GetAxis("Horizontal");float vertical = Input.GetAxis("Vertical");Vector3 dir = new Vector3(horizontal, 0, vertical);if (dir != Vector3.zero){transform.rotation = Quaternion.LookRotation(dir);animator.SetBool("isRun", true);transform.Translate(Vector3.forward * 2 * Time.deltaTime);}else{animator.SetBool("isRun", false);}}
}
运行!
相关文章:

Unity3D 创建一个人物,实现人物的移动
1,创建项目 首先打开我们的Unity Hub 在我们的编译器下面新建项目,选择3D模板,更改一下我们的项目名称,选择一下路径,然后点击创建项目 等待项目创建。。。。。。 我们在项目里先创建一个plane,这样有点视…...

【笔记】数据结构12
文章目录 2013年408应用题41方法一方法二 看到的社区的一个知识总结,这里记录一下。 知识点汇总 2013年408应用题41 解决方法: 方法一 (1)算法思想 算法的策略是从前向后扫描数组元素,标记出一个可能成为主元素的元…...

django的URL配置
1 django如何处理一个请求 首先Django要使用根URLconf模块,通过setting.py配置文件的ROOT_URLCONF来设置。 加载该模块后并查找变量 urlpatterns。这是一个Python的django.conf.urls.url()实例列表。 Django按顺序运行每个URL模式,并在匹配所请求的…...

精华帖分享 | 因子构建思考1
本文来源于量化小论坛股票量化板块精华帖,作者为z-coffee。 以下为精华帖正文: 一段时间没写帖子,其实一直在研究策略,只是从不同的角度去思考而已。熟悉我的老板其实清楚,我的炉子水平一般,基本不太依托…...
)
kubernetes笔记(四)
一、Pod调度策略 1.基于节点的调度 spec->nodeName [rootmaster ~]# vim myhttp.yaml --- kind: Pod apiVersion: v1 metadata:name: myhttp spec:nodeName: node-0001 # 基于节点名称进行调度containers:- name: apacheimage: myos:httpd[rootmaster ~]# kubectl a…...

通信工程学习:什么是SNMP简单网络管理协议
SNMP:简单网络管理协议 SNMP(Simple Network Management Protocol,简单网络管理协议)是一种用于在计算机网络中管理网络节点(如服务器、工作站、路由器、交换机等)的标准协议。它属于OSI模型的应用层&#…...

ubuntu20.04系统下,c++图形库Matplot++配置
linux下安装c图形库Matplot,使得c可以可视化编程;安装Matplot之前,需要先安装一个gnuplot,因为Matplot是依赖于此库 gnuplot下载链接: http://www.gnuplot.info/ 一、gnuplot下载与安装(可以跳过,下面源码…...

[激光原理与应用-126]:南京科耐激光-激光焊接 - 焊中无损检测技术 - 智能制程监测系统IPM介绍 - 26- 频域分析法
目录 一、什么是频域分析法 1、定义 2、基本原理 3、分析步骤 4、应用领域 5、优缺点 二、频域分析法在激光焊接故障监测中的应用 2.1 概述 1、应用背景 2、频域分析法的应用 3、应用优势 4、应用实例 2.2 激光焊接故障检测中光电信号的频谱特征 1、光电信号分类…...
:功能、应用与最佳实践)
深入理解 Solidity 修饰符(Modifier):功能、应用与最佳实践
1. 什么是修饰符(Modifier)? 1.1 修饰符的定义 在 Solidity 中,修饰符(Modifier)是一种用于更改函数行为的关键字。它们可以用于控制函数的执行条件、添加前置检查、简化重复逻辑等。修饰符在函数执行之前…...

YOLO11项目实战1:道路缺陷检测系统设计【Python源码+数据集+运行演示】
一、项目背景 随着城市化进程的加速和交通网络的不断扩展,道路维护成为城市管理中的一个重要环节。道路缺陷(如裂缝、坑洞、路面破损等)不仅影响行车安全,还会增加车辆的磨损和维修成本。传统的道路缺陷检测方法主要依赖人工巡检…...

怎么屏蔽统计系统统计到的虚假ip
屏蔽统计系统中的虚假IP是保护网站分析数据准确性的重要措施。以下是一些有效的策略和步骤,可以帮助您过滤掉虚假IP: 1. 识别虚假IP的特征 了解虚假IP的常见特征可以帮助您识别和屏蔽它们: 短时间内高频率访问:虚假IP可能会在短…...

前端开发设计模式——策略模式
目录 一、策略模式的定义和特点 1.定义: 2.特点: 二、策略模式的实现方式 1.定义策略接口: 2.创建具体策略类: 3.定义上下文类: 三、策略模式的应用场景 1.表单验证场景: 2.动画效果切换场景&…...
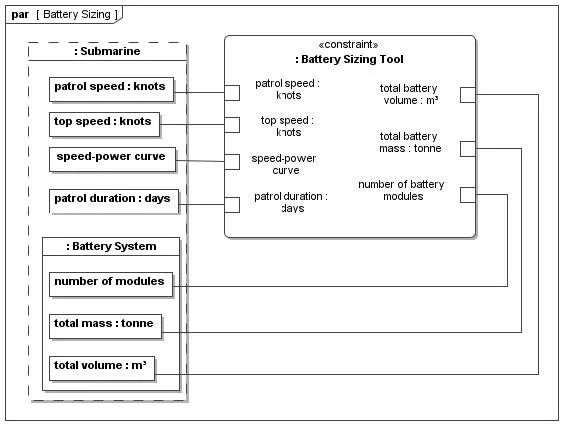
SysML案例-潜艇
DDD领域驱动设计批评文集>> 《软件方法》强化自测题集>> 《软件方法》各章合集>>...

车辆重识别(2020NIPS去噪扩散概率模型)论文阅读2024/9/27
[2] Denoising Diffusion Probabilistic Models 作者:Jonathan Ho Ajay Jain Pieter Abbeel 单位:加州大学伯克利分校 摘要: 我们提出了高质量的图像合成结果使用扩散概率模型,一类潜变量模型从非平衡热力学的考虑启发。我们的最…...

基于深度学习的任务序列中的快速适应
基于深度学习的任务序列中的快速适应是指模型在接连处理不同任务时,能够迅速调整和优化自身以适应新任务的能力。这种能力在动态环境和多任务学习中尤为重要,旨在减少训练时间和资源需求。以下是这一主题的关键要素: 1. 快速适应的背景 动态…...

虚拟机三种网络模式详解
在电脑里开一台虚拟机,是再常见不过的操作了。无论是用虚拟机玩只有旧版本系统能运行的游戏,还是用来学习Linux、跑跑应用程序都是很好的。而这其中,虚拟机网络是绝对绕不过去的。本篇文章通俗易懂的介绍了常见的虚拟网络提供的三种网络链接模…...

[leetcode]674_最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。 连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l < i < r,都有 nums[i] < nums[i 1] &am…...

【无人机设计与技术】四旋翼无人机,UAV仿真,轨迹跟踪PID控制
摘要 本文探讨了四旋翼无人机(UAV)在轨迹跟踪中的PID控制仿真方法。通过设计三轴方向的PID控制器,调节无人机的姿态与位置,使其能够准确跟踪预设轨迹。本文使用MATLAB/Simulink进行了建模与仿真,验证了PID控制算法在无…...

回归预测|基于卷积神经网络-支持向量机的数据回归预测Matlab程序CNN-SVM 卷积提取特征与原始特征进行融合预测
回归预测|基于卷积神经网络-支持向量机的数据回归预测Matlab程序CNN-SVM 卷积提取特征与原始特征进行融合预测 文章目录 一、基本原理原理流程总结 二、实验结果三、核心代码四、代码获取五、总结 回归预测|基于卷积神经网络-支持向量机的数据回归预测Matlab程序CNN-SVM 卷积提…...

javaScript基础知识汇总
一、基础语法 1、区分大小写:无论是变量、函数名还是操作符,都区分大小写。 2、标识符:就是变量、函数、属性或函数参数的名称。标识符可以由一个或多个字符构成,但需要满足以下条件: 第一个字符必须是一个字母、下…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
