信息学奥赛一本通 1416:【17NOIP普及组】棋盘 | 洛谷 P3956 [NOIP2017 普及组] 棋盘
【题目链接】
洛谷 P3956 [NOIP2017 普及组] 棋盘
ybt 1416:【17NOIP普及组】棋盘
【题目考点】
1. 深搜:深搜回溯
2. 深搜剪枝:最优化剪枝
【解题思路】
搜索从左上角到右下角的所有走法中花费金币最少的走法。
需要使用深搜回溯,搜索从一点出发到另一点的所有路径。
设二维数组mp记录每个格子的颜色,如果无色记为-1,1是黄色,0是红色。
在某次搜索时,当前位置为(sx, sy),下一个要访问的位置为(x, y),已经使用金币coin。
如果当前位置(sx,sy)是有色的
- 如果下一个位置(x,y)是有色的
- 如果二者颜色相同,到下个位置时花的金币数coin不变
- 如果颜色不同,到下个位置花的金币数coin加1。
- 如果下一个位置(x,y)是无色的
- 将下一个位置通过魔法变为与(sx, sy)同色,到下个位置的金币数coin加2,
如果当前位置(sx, sy)是无色的,但是变成了col色。那么下个位置(x, y)不可以是无色的。
如果下个位置(x,y)是有色的,那么
- 如果(x,y)位置的颜色和col相同,那么到下个位置时花的金币数coin不变
- 如果(x,y)位置的颜色和col不同,到下个位置花的金币数coin加1。
设二维数组mc,mc[i][j]表示到达(i, j)位置时花的最少金币数。
最优性剪枝:如果到(sx, sy)位置花的钱数coin比已知的一种到(sx, sy)位置的走法花钱mc[sx][sy]相等或更多,则没必要再搜索了,直接返回。
这里必须进行最优性剪枝,否则搜索会超时。
【题解代码】
解法1:深搜
#include<bits/stdc++.h>
using namespace std;
#define N 105
#define INF 0x3f3f3f3f
int m, n, mp[N][N], minCoin = INF, mc[N][N];//mp[i][j]:为1代表黄色,0代表红色,-1代表无色 mc[i][j],到i,j的最小钱数
int dir[4][2] = {{0,1},{0,-1},{-1,0},{1,0}};
bool vis[N][N];
void dfs(int sx, int sy, int coin, int col)//col:如果(sx,sy)本来是无色,col为(sx,sy)通过魔法变化后的颜色
{if(coin >= mc[sx][sy])//最优化剪枝,如果到当前位置花的钱数比已知的一种到当前位置的走法花钱更多,则没必要再搜索了。 return;elsemc[sx][sy] = coin;if(sx == m && sy == m)//到达终点点 return; for(int i = 0; i < 4; ++i){int x = sx + dir[i][0], y = sy + dir[i][1];//x,y是sx,sy周围的位置 if(x >= 1 && x <= m && y >= 1 && y <= m && !vis[x][y]){vis[x][y] = true;if(mp[sx][sy] == 1 || mp[sx][sy] == 0)//如(sx, sy)是红黄 {if(mp[x][y] == -1)//如果下一个位置无色 dfs(x, y, coin + 2, mp[sx][sy]);//变成与出发点相同的颜色 else if(mp[x][y] == mp[sx][sy])//颜色相同 dfs(x, y, coin, -1);else//颜色不同 dfs(x, y, coin + 1, -1);}else if(mp[sx][sy] == -1 && mp[x][y] != -1)//如(sx, sy)是无色 {//如果无色的下一个格子还是无色,则不访问 if(mp[x][y] == col)//颜色相同 dfs(x, y, coin, -1); else//颜色不同 dfs(x, y, coin + 1, -1);}vis[x][y] = false;}}
}
int main()
{int x, y, c;memset(mp, -1, sizeof(mp));cin >> m >> n;for(int i = 1; i <= n; ++i){cin >> x >> y >> c;mp[x][y] = c;}memset(mc, 0x3f, sizeof(mc));dfs(1, 1, 0, -1);if(mc[m][m] == INF)cout << -1;elsecout << mc[m][m];return 0;
}
相关文章:

信息学奥赛一本通 1416:【17NOIP普及组】棋盘 | 洛谷 P3956 [NOIP2017 普及组] 棋盘
【题目链接】 洛谷 P3956 [NOIP2017 普及组] 棋盘 ybt 1416:【17NOIP普及组】棋盘 【题目考点】 1. 深搜:深搜回溯 2. 深搜剪枝:最优化剪枝 【解题思路】 搜索从左上角到右下角的所有走法中花费金币最少的走法。 需要使用深搜回溯&…...
UE4完整教程 UE4简介 UE4学习攻略及文件格式
开头附上工作招聘面试必备问题噢~~包括综合面试题、无领导小组面试题资源文件免费!全文干货。 UE4简介学习攻略UE4Demo代码面试内容资源-CSDN文库https://download.csdn.net/download/m0_72216164/89825102 工作招聘无领导小组面试全攻略最常见面试题(第一部分)共有17章+可…...

JVM内存回收机制
目录 1.JVM运行时数据区 2.JVM类加载过程 3.双清委派模型 4.垃圾回收机制(GC) 找出谁是垃圾方案一:引用计数 找出谁是垃圾:方案二,可达性分析 释放垃圾的内存空间 判断垃圾:jvm依据对象的年龄对 对象…...

中国身份证号码校验
题目描述 第二届河南省最美教师评选开始了,每一位同学都可以投票选出你支持的人选,但是为了防止刷票,必须通过身份验证才可投票。负责投票平台后台的老大爷希望你能帮他验证身份证号的合法性,防止那些熊孩子随意刷票,…...

【Kubernetes】常见面试题汇总(五十四)
目录 120.创建 init C 容器后,其状态不正常? 特别说明: 题目 1-68 属于【Kubernetes】的常规概念题,即 “ 汇总(一)~(二十二)” 。 题目 69-113 属于【Kubernetes】的生产…...

不懂外语也能无障碍交流?探索4款超好用中英翻译工具
嘿,各位外贸流程的小伙伴们,今儿咱们来聊聊那些翻译神器,看看它们在中英文互译这条路上,是怎么给我们这些天天跟洋文打交道的哥们儿姐们儿减轻负担的。我亲身体验了福昕翻译在线、福昕翻译大师、海鲸AI翻译还有腾讯翻译君…...

C++ WebDriver扩展
概述 WebDriver协议基于HTTP,使用JSON进行数据传输,定义了client与driver之间的通信标准。无论client的实现语言(如Java或C#),都能通过协议中的endpoints准确指示driver执行各种操作,覆盖了Selenium的所有功…...

WeChat_DevTools 断点调试方法总结
新建工程,以小程序 login 调试为例,代码如下: // 登录wx.login({success: res > {// 发送 res.code 到后台换取 openId, sessionKey, unionIddebugger;resThis this;wx.showModal({title: 登录成功,content: res.code res.code,comple…...
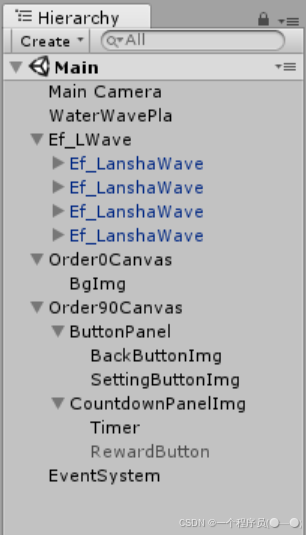
水波荡漾效果+渲染顺序+简单UI绘制
创建场景及布置 创建新场景Main,在Main场景中创建一个plane物体,命名为WaterWavePla,具体数值及层级面板排布如下: 编写脚本 创建一个文件夹,用于存放脚本,命名Scripts,创建一个子文件夹Effect,存放特效相关脚本,创建…...

深度学习中的结构化概率模型 - 使用图来描述模型结构篇
序言 在深度学习的探索之路上,结构化概率模型以其独特的视角和强大的表达能力,成为了研究复杂数据关系的重要工具。这一模型的核心在于其巧妙地利用图来描述模型结构,将随机变量间的复杂交互关系可视化、结构化。图的引入,不仅为…...

C语言中的栈帧
------------------------ | 局部变量区 | | (根据变量声明而变化) | ------------------------ | 参数区 | | (根据函数原型而变化) | ------------------------ | (可选) 保存寄存器区 | | (编译器/架构特定) | -…...

vue数组根据某些条件进行二次切割
原本的一个一维数组首先 1.根据depnm和bed的不同会分成不同的数组 2.在条件1的基础上分割出来的数组如果存在里面有isBgn1的会进行二次分割 比如原数组是[{depnm:1,bed:2,isBgn:0},{}……] 根据条件一会组成一个二维数组得到 [ [①depnm值一致的一个一维数组], [②bed值一…...

Yolov8改进轻量级网络Ghostnetv2
1,理论部分 轻量级卷积神经网络 (CNN) 专为移动设备上的应用程序而设计,具有更快的推理速度。卷积运算只能捕获窗口区域中的局部信息,这会阻止性能进一步提高。将自我注意引入卷积可以很好地捕获全局信息,但会在很大程度上阻碍实际速度。在本文中,我们提出了一种硬件友好…...
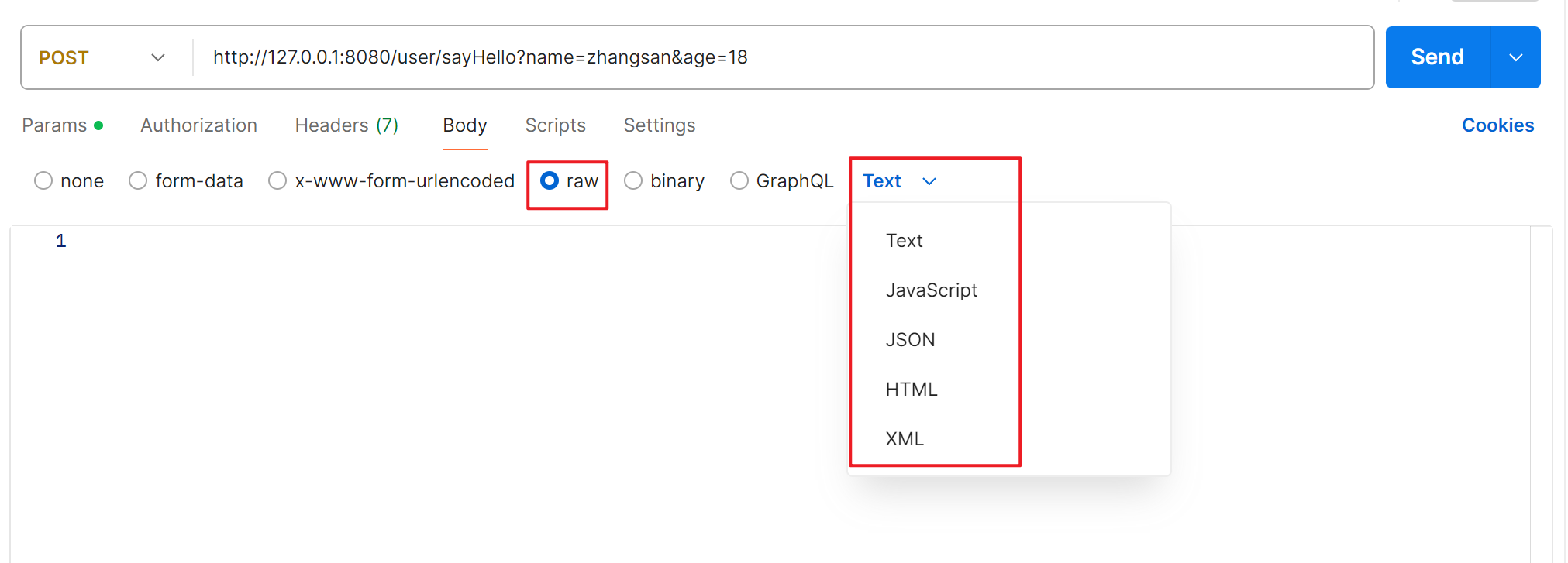
【Spring】@RequestMapping、@RestController和Postman
文章目录 1.RequestMapping 注解介绍2. RequestMapping 使用3. RequestMapping 是 GET 还是 POST 请求?GET 请求POST 请求指定 GET/POST 方法类型 2. Postman 介绍1. 创建请求2. 传参介绍1. 普通传参2. form-data3. x-www-form-urlencoded form 表单,对应…...
详细理解并附实现代码。)
【深度学习基础模型】回声状态网络(Echo State Networks, ESN)详细理解并附实现代码。
【深度学习基础模型】回声状态网络(Echo State Networks, ESN)详细理解并附实现代码。 【深度学习基础模型】回声状态网络(Echo State Networks, ESN)详细理解并附实现代码。 文章目录 【深度学习基础模型】回声状态网络…...

Redis的基础认识与在ubuntu上的安装教程
来自Redis的自我介绍 我是Redis,一个中间件,职责是把数据存储在内存上,因此可以作为数据库、缓存、消息队列等场景使用。由于可以把数据存储在内存上,因此江湖人称快枪手 1.redis的功能特性 (1)数据在内存…...

鸿蒙harmonyos next flutter混合开发之ohos工程引用 har 文件
创建鸿蒙原生工程MyApplication。创建flutter module,生成har文件,并且将flutter module中.ohos文件entryability/EntryAbility.ets、pages/Index.ets分别替换MyApplication中的。 # 1. 创建 flutter子模块工程 flutter create -t module my_flutter_…...

react-问卷星项目(5)
实战 路由 路由设计,网址和页面的关系,就是从业务上分析需要哪些页面哪些页面内容可以抽离,业务流程要有入有出增加页面和Layout模版,模版就是抽离页面公共部分,比如都有顶部或者左侧导航,直接上代码&…...

08.useInterval
在 React 应用中,实现定时器功能通常需要使用 setInterval() 和 clearInterval(),这可能会导致代码复杂和难以维护。useInterval 钩子提供了一种声明式的方法来实现定时器功能,使得定时器的管理更加简单和直观。这个自定义钩子不仅简化了定时器的使用,还解决了一些常见的定…...

【Android 源码分析】Activity生命周期之onDestroy
忽然有一天,我想要做一件事:去代码中去验证那些曾经被“灌输”的理论。 – 服装…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

Python爬虫(52)Scrapy-Redis分布式爬虫架构实战:IP代理池深度集成与跨地域数据采集
目录 一、引言:当爬虫遭遇"地域封锁"二、背景解析:分布式爬虫的两大技术挑战1. 传统Scrapy架构的局限性2. 地域限制的三种典型表现 三、架构设计:Scrapy-Redis 代理池的协同机制1. 分布式架构拓扑图2. 核心组件协同流程 四、技术实…...
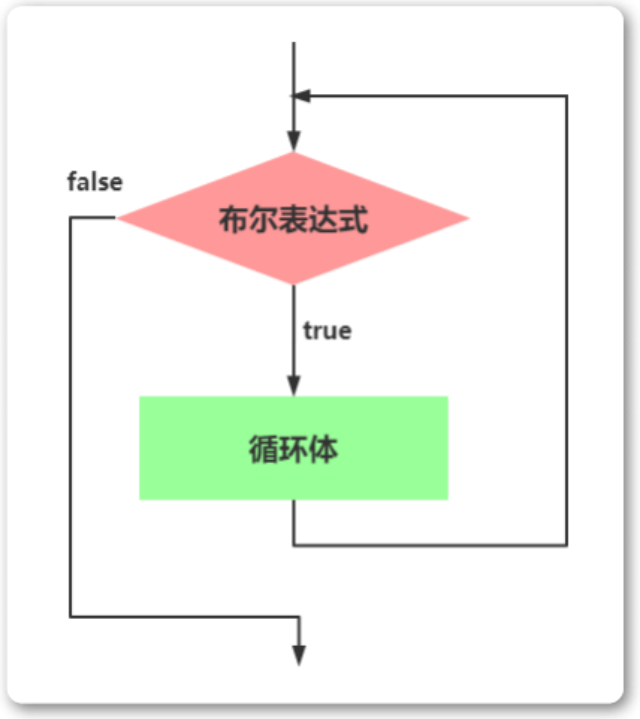
循环语句之while
While语句包括一个循环条件和一段代码块,只要条件为真,就不断 循环执行代码块。 1 2 3 while (条件) { 语句 ; } var i 0; while (i < 100) {console.log(i 当前为: i); i i 1; } 下面的例子是一个无限循环,因…...
