代码随想录 | Day26 | 二叉树：二叉搜索树中的插入操作删除二叉搜索树中的节点修剪二叉搜索树

代码随想录 | Day26 | 二叉树：二叉搜索树中的插入操作&&删除二叉搜索树中的节点&&修剪二叉搜索树

主要学习内容：
二叉搜索树的插入删除操作

701.二叉搜索树中的插入操作

701. 二叉搜索树中的插入操作 - 力扣（LeetCode）

解法思路：

本质就是二叉搜索树的查找，找到插入的地方就行

val比本层结点t的值大，去右子树，小，去左子树，如果左子树或者右子树为空，直接把val赋值给它就完事。

1.函数参数和返回值

void tra(TreeNode *t,int val)

t当前节点，val是插入值

2.终止条件

本题只要赋值操作结束就是终止条件

3.本层代码逻辑

		//比本层小，去左子树if(t->val>val)if(t->left)tra(t->left,val);//左子树为空，直接赋值返回else{t->left=new TreeNode(val);return;}//比本层大，去右子树elseif(t->right)tra(t->right,val);//右子树为空，直接赋值返回else{t->right=new TreeNode(val);return;}

完整代码：

class Solution {
public:void tra(TreeNode *t,int val){if(t->val>val)if(t->left)tra(t->left,val);else{t->left=new TreeNode(val);return;}elseif(t->right)tra(t->right,val);else{t->right=new TreeNode(val);return;}}TreeNode* insertIntoBST(TreeNode* root, int val) {if(root==nullptr){root=new TreeNode(val);return root;}tra(root,val);return root;}
};

注意一下检查root是否为空就行

代码随想录做法

class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if (root == NULL) {TreeNode* node = new TreeNode(val);return node;}if (root->val > val) root->left = insertIntoBST(root->left, val);if (root->val < val) root->right = insertIntoBST(root->right, val);return root;}
}

搜索过程：

if (root->val > val) root->left = insertIntoBST(root->left, val);
if (root->val < val) root->right = insertIntoBST(root->right, val);

赋值过程：

        if (root == NULL) {TreeNode* node = new TreeNode(val);return node;}

比自己写的要简洁很多，特殊情况也涵盖了进去

450.删除二叉搜索树中的节点

450. 删除二叉搜索树中的节点 - 力扣（LeetCode）

思路：

先分情况讨论，没找到就不说啦，找到的话可以大致分为3种情况

1.删除的是叶子结点，直接删

2.删的结点只有一个孩子，左或者右，那就让孩子直接继承到结点所在的位置即可

3.删的结点左右都有，这个比较麻烦，我选择的策略是把当前结点的左孩子接到右孩子上面。而这样的话，我们就要找到当前结点右孩子的最左边的左孩子，让当前结点的左孩子接上去，因为这里是只比当前结点大一点点的数，比当前结点的其他数都要小，只有在这里才符合二叉搜索树定义。

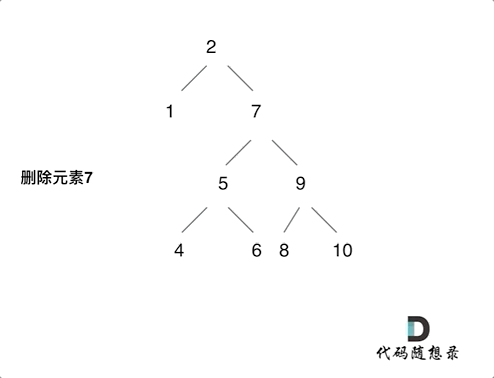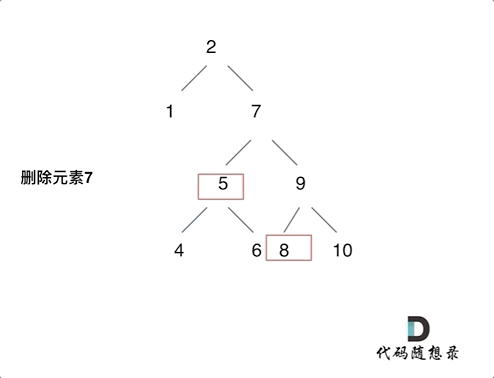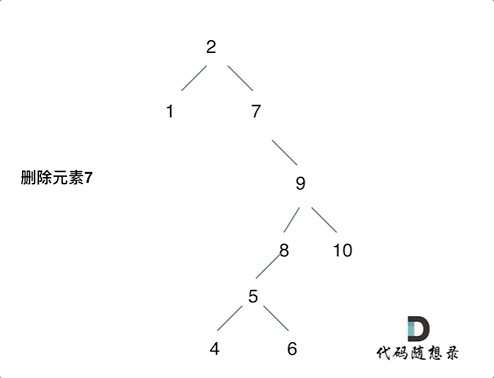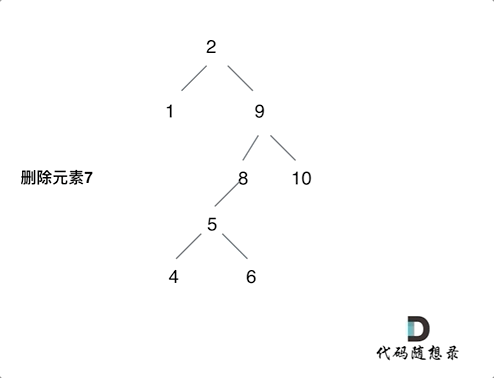
例如删除7的过程，就是如上。如果没有8的话，那5也是直接去8的位置。

接下来看具体的代码实现

1.函数返回值和参数

TreeNode* deleteNode(TreeNode* root, int key) 

我们直接就返回的是删除完以后的当前结点，可能是当前结点被删，也有可能是左子树或者右子树中的结点被删掉，然后一层一层往上返回。

2.本层逻辑

if(root->val>key)  root->left=deleteNode(root->left,key);
if(root->val<key) root->right=deleteNode(root->right,key);
return root;

左子树不为空，遍历左子树，用当前结点的左子树承接修改完以后的左子树根结点

右子树不为空，遍历右子树，用当前结点的右子树承接修改完以后的右子树根结点

左右子树处理完以后返回当前结点

如果删除的是本层结点的话，会在终止条件中处理

3.终止条件（其实我觉得也算是本层处理逻辑了）

步骤：

1.为空那就返回null

2.如果没找到那就跳到本层逻辑去继续递归左右子树

3.找到了的话就是进入下面这个if

​ 3.1 叶子结点 直接删

​ 3.2 左为空或者右为空 直接让孩子继承当前结点的位置，左不为空就返回左孩子，这里是通过本层逻辑里面的root->left承接住了这个返回值，右孩子同理

​ 3.3 左右都不为空

TreeNode *t=root->right;
while(t->left) t=t->left;
t->left=root->left;
return root->right;  

1.保存一下右孩子，因为我们的策略是让左孩子接到右孩子上面。

2.找到右子树中最左边的位置，即一直循环，循环到空为止

3.将当前结点左孩子移动到右子树最左边

4.返回新的子树的根结点，即当前结点的右子树

完整的本层逻辑代码：

if(root==nullptr)return nullptr;
if(root->val==key)
{if(root->left==nullptr&&root->right==nullptr)return nullptr;else if(root->left!=nullptr&&root->right==nullptr)return root->left;else if(root->left==nullptr&&root->right!=nullptr)return root->right;else{TreeNode *t=root->right;while(t->left) t=t->left;t->left=root->left;return root->right;  } 
}

完整代码：

class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if(root==nullptr)return nullptr;if(root->val==key){if(root->left==nullptr&&root->right==nullptr)return nullptr;else if(root->left!=nullptr&&root->right==nullptr)return root->left;else if(root->left==nullptr&&root->right!=nullptr)return root->right;else{TreeNode *t=root->right;while(t->left) t=t->left;t->left=root->left;return root->right;  } }if(root->val>key)  root->left=deleteNode(root->left,key);if(root->val<key) root->right=deleteNode(root->right,key);return root;}
};

注意我们这里是逻辑上的修改，物理上还需要手动释放内存，这里不过多赘述，大家自行注意。

代码随想录有释放内存的完整版：

class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root; // 第一种情况：没找到删除的节点，遍历到空节点直接返回了if (root->val == key) {// 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点if (root->left == nullptr && root->right == nullptr) {///! 内存释放delete root;return nullptr;}// 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点else if (root->left == nullptr) {auto retNode = root->right;///! 内存释放delete root;return retNode;}// 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点else if (root->right == nullptr) {auto retNode = root->left;///! 内存释放delete root;return retNode;}// 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置// 并返回删除节点右孩子为新的根节点。else {TreeNode* cur = root->right; // 找右子树最左面的节点while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要删除的节点（root）左子树放在cur的左孩子的位置TreeNode* tmp = root;   // 把root节点保存一下，下面来删除root = root->right;     // 返回旧root的右孩子作为新rootdelete tmp;             // 释放节点内存（这里不写也可以，但C++最好手动释放一下吧）return root;}}if (root->val > key) root->left = deleteNode(root->left, key);if (root->val < key) root->right = deleteNode(root->right, key);return root;}
};

669.修剪二叉搜索树

669. 修剪二叉搜索树 - 力扣（LeetCode）

思路1：上一套题的后序遍历

上一道题是判断等不等于，这道题是判断是否在一个区间没错就改一个if条件就好。

哈哈其实没有那么简单，上一套道题本质上是一个前序遍历，我们找到一个符合的值，删掉了就直接return了，没管它的子树上的值有没有在区间内，所以我们这次要换成后序遍历，这样就是从最底下开始遍历，每一个节点都不会错过。

class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if(root==nullptr)return nullptr;//左if(root->left)  root->left=trimBST(root->left,low,high);//右if(root->right) root->right=trimBST(root->right,low,high);//中if(root->val>high || root->val<low){if(root->left==nullptr&&root->right==nullptr)return nullptr;else if(root->left!=nullptr&&root->right==nullptr)return root->left;else if(root->left==nullptr&&root->right!=nullptr)return root->right;else{TreeNode *t=root->right;while(t->left) t=t->left;t->left=root->left;return root->right;  } }return root;}
};

思路2：后序遍历

class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if(root==nullptr)return nullptr;root->left=trimBST(root->left,low,high);root->right=trimBST(root->right,low,high);if(root->val<low)return root->right;if(root->val>high)return root->left;return root;}
};

后序遍历，本层逻辑是如果遇到小于low的直接返回右孩子，大于high的直接返回左孩子。

有人可能疑惑这样的话不就不知道右孩子和左孩子是否全都符合区间了嘛？

其实后序遍历就避免了这个问题，我们看一个例子

我们是后序遍历，所以先遍历到1发现1是，再到2，再到0发现0小于low，就返回右孩子，遍历4,4大于high，返回左孩子。

你会发现我们用后序遍历，左子树或者右子树的结点全是已经验证过的，留下的都是在区间内的。

思路3：（复习的时候再看一遍）

对根结点 root 进行深度优先遍历。对于当前访问的结点，如果结点为空结点，直接返回空结点；如果结点的值小于 low，那么说明该结点及它的左子树都不符合要求，我们返回对它的右结点进行修剪后的结果；如果结点的值大于 high，那么说明该结点及它的右子树都不符合要求，我们返回对它的左子树进行修剪后的结果；如果结点的值位于区间 [low,high]，我们将结点的左结点设为对它的左子树修剪后的结果，右结点设为对它的右子树进行修剪后的结果。

class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (root == nullptr) {return nullptr;}if (root->val < low) {return trimBST(root->right, low, high);} else if (root->val > high) {return trimBST(root->left, low, high);} else {root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);return root;}}
};