堆排序算法的原理与应用
堆排序(Heap Sort)是一种基于堆数据结构的比较排序算法。它具有时间复杂度为 O(n log n) 的优点,并且空间复杂度为 O(1),是一种不稳定的排序算法。本文将详细介绍堆排序的工作原理、步骤以及它的应用场景。
一、堆排序的基本概念
堆是一种特殊的二叉树数据结构,具有以下两个重要特性:
- 完全二叉树:所有的层都是满的,除了最后一层,且最后一层的节点从左到右依次排列。
- 堆的性质:
- 最大堆:对于每个非叶子节点,父节点的值都大于或等于其子节点的值。
- 最小堆:对于每个非叶子节点,父节点的值都小于或等于其子节点的值。
堆排序的核心思想是:利用堆这种结构,每次将堆顶元素(最大或最小)取出,然后调整剩余的堆,直到所有元素都被排好序。
1. 堆排序的流程
堆排序的基本过程可以分为以下几个步骤:
- 构建最大堆:将无序数组调整为一个符合最大堆性质的结构。
- 取出堆顶元素:将最大堆的根节点(即最大值)与最后一个节点交换,并把最大值放在数组末尾。此时,最大值已在正确的位置。
- 重新调整堆:去掉已排好的元素,重新调整剩下的部分,使其再次成为一个最大堆。
- 重复步骤 2 和 3:直到堆中只剩下一个元素,排序完成。
二、堆排序的详细步骤
接下来,我们具体看看如何实现堆排序。以下是堆排序的步骤说明:
1. 构建最大堆
将一个无序数组变成一个最大堆的过程称为堆化。堆化的过程是从最后一个非叶子节点开始,自底向上依次调整每个节点,使其符合最大堆的性质。堆化的时间复杂度为 O(n)。
2. 取出堆顶元素
最大堆的堆顶元素是整个数组的最大值。将这个值与数组的最后一个元素交换,并缩小堆的范围(忽略已排好序的部分)。这时,堆顶可能不再是最大值,需要通过堆调整重新恢复最大堆的性质。
3. 堆调整
堆调整是保持堆的性质的核心操作。每次调整时,将新的堆顶元素下沉到合适的位置,确保每个父节点都大于等于它的子节点。堆调整的时间复杂度是 O(log n),因为树的高度是 log n。
4. 重复构建和调整
重复取出堆顶元素和堆调整,直到所有元素排序完毕。由于每次取出一个元素都需要堆调整,因此总的时间复杂度为 O(n log n)。
代码示例
为了让读者更直观理解堆排序的实现,下面是堆排序的伪代码描述:
# 堆排序主函数
def heap_sort(arr):n = len(arr)# 1. 构建最大堆for i in range(n // 2 - 1, -1, -1):heapify(arr, n, i)# 2. 取出堆顶元素并重新调整堆for i in range(n - 1, 0, -1):arr[i], arr[0] = arr[0], arr[i] # 交换堆顶与最后一个元素heapify(arr, i, 0) # 重新调整堆# 堆调整函数
def heapify(arr, n, i):largest = i # 初始化当前节点为最大left = 2 * i + 1 # 左子节点right = 2 * i + 2 # 右子节点# 如果左子节点存在且大于父节点if left < n and arr[left] > arr[largest]:largest = left# 如果右子节点存在且大于父节点if right < n and arr[right] > arr[largest]:largest = right# 如果最大值不是父节点,则进行交换,并继续调整if largest != i:arr[i], arr[largest] = arr[largest], arr[i]heapify(arr, n, largest)
在上面的代码中,heap_sort 函数是堆排序的主函数,而 heapify 函数负责维护最大堆的性质。每次调整完堆后,最大的元素会被移到数组的末尾,剩下的部分继续调整直到整个数组有序。
三、堆排序的优缺点
优点
- 时间复杂度稳定:堆排序的时间复杂度始终为 O(n log n),无论输入数据的有序程度如何。
- 空间复杂度为 O(1):堆排序是一种原地排序算法,不需要额外的辅助空间。
- 不受输入数据影响:堆排序的效率不依赖于输入数据是否有序,在最坏、最好和平均情况下的时间复杂度都为 O(n log n)。
缺点
- 不稳定:堆排序是一种不稳定排序算法,也就是说,相同的元素在排序前后可能会改变相对顺序。
- 常数开销大:尽管时间复杂度为 O(n log n),但由于堆的调整操作涉及较多次的交换,导致实际性能可能不如其他 O(n log n) 的排序算法(如归并排序和快速排序)。
四、堆排序的应用场景
堆排序由于其 O(n log n) 的时间复杂度和 O(1) 的空间复杂度,适合用于内存有限且需要稳定性能的场景。例如:
- 大数据量排序:在大数据量排序中,堆排序表现较为稳定,并且由于其空间复杂度低,适合在内存有限的设备上进行排序任务。
- 优先级队列:堆排序常用于实现优先级队列。通过最大堆或最小堆,可以快速找到队列中最大或最小的元素。
- 实时排序系统:堆排序适合在需要随时调整数据顺序的系统中,如实时交易系统、调度系统等。
五、总结与讨论
堆排序作为一种高效且节省空间的排序算法,在许多大数据和系统应用中都有其独特的优势。尽管它在实际应用中的普及程度不如快速排序,但在某些特殊场景下,它凭借稳定的时间复杂度和原地排序的特性,仍然是一个有力的选择。你在实际开发中有没有遇到过需要选择堆排序的情况?相比其他排序算法,你认为它在哪些应用场景下表现更好?欢迎分享你的经验和看法!
相关文章:

堆排序算法的原理与应用
堆排序(Heap Sort)是一种基于堆数据结构的比较排序算法。它具有时间复杂度为 O(n log n) 的优点,并且空间复杂度为 O(1),是一种不稳定的排序算法。本文将详细介绍堆排序的工作原理、步骤以及它的应用场景。 一、堆排序的基本概念…...

【2024版本】Mac/Windows IDEA安装教程
IDEA 2024版本真的很强大,此外JDK发布了最新稳定版 JDK21 ,只有新版本支持JDK 21、JDK22。原来数据库插件不支持redis等一些NoSql的数据库的连接,如果要使用需要自己单独装收费的插件。直接打开idea就很吃内存了,再打开其他一大堆…...

Oracle bbed编译安装及配置
1. 什么是bbed ? Oracle Block Brower and EDitor Tool,是一个可以对oracle data block进行查看,编辑修改的内置工具。对于bbed,oracle本身是不提供支持的。 2. 如何编译bbed环境? 10g版本: 1) 编译bbed cd $ORACL…...

MindSearch 部署到Github Codespace 和 Hugging Face Space
conda init后需要重开终端,不然一键复制会导致后续pip install会安装错环境 还是报错 ImportError: cannot import name AutoRegister from class_registry (/opt/conda/envs/mindsearch/lib/python3.10/site-packages/class_registry/__init__.py)pip install --…...
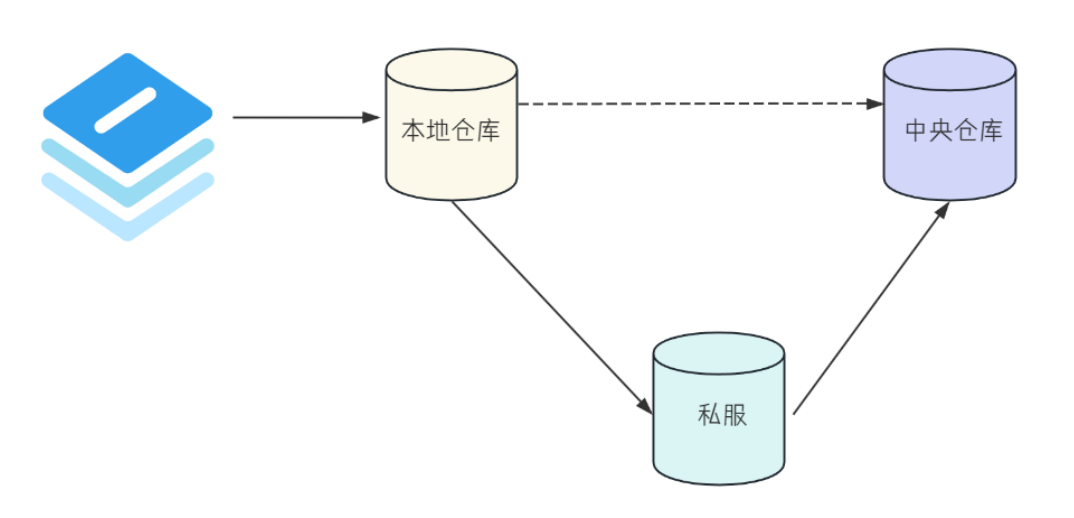
【Maven】依赖管理,Maven仓库,Maven核心功能
Maven 是一个项目管理工具,基于 POM(Project Object Model,项目对象模型)的概念,Maven 可以通过一小段描述信息来管理项目的构建,报告和文档的项目管理工具软件 大白话:Maven 是一个项目管理工…...

Android wifi信号和漫游信号设置
1.wifi信号 /packages/modules/Wifi/framework/java/android/net/wifi/WifiManager.java Deprecated public static int calculateSignalLevel(int rssi, int numLevels) { if (rssi < MIN_RSSI) { //*/update wifi signal return 1;…...

检查cuda和显卡的可用性
检查cuda和显卡的可用性 import torch device_gpu torch.device(cuda if torch.cuda.is_available() else cpu) print(device_gpu) print(torch.cuda.is_available())...

Kotlin:2.0.20 的新特性
一、概述 Kotlin 2.0.20英文版官方文档 Kotlin 2.0.20发布了!这个版本包括对Kotlin 2.0.0的性能改进和bug修复,我们在其中宣布Kotlin K2编译器为Stable。以下是本次发布的一些亮点: 数据类复制函数将具有与构造函数相同的可见性来自默认目标层次结构的源集的静态访…...

Python内存管理与泄漏排查实战
Python内存管理与泄漏排查实战 Python作为一种高级编程语言,因其易读性和丰富的标准库而备受开发者青睐。然而,随着项目的复杂度增加,内存管理问题可能会影响程序的性能,甚至导致内存泄漏。为了构建健壮且高效的应用程序…...

828华为云征文|华为云Flexus云服务器X实例搭建部署H5美妆护肤分销商城、前端uniapp
准备国庆之际,客户要搭个 H5 商城系统,这系统好不容易开发好啦,就差选个合适的服务器上线。那可真是挑花了眼,不知道哪款性价比高呀!就像在琳琅满目的选择前。最终慧眼识珠,选择了华为云 Flexus X。至于为什…...

初学51单片机之I2C总线与E2PROM二
总结下上篇博文的结论: 1:ACK信号在SCL为高电平期间会一直保持。 2:在字节数据传输过程中如果发送电平跳变,那么电平信号就会变成重复起始或者结束的信号。(上篇博文的测试方法还是不能够明确证明这个结论࿰…...
Kafka学习笔记(一)Kafka基准测试、幂等性和事务、Java编程操作Kafka
文章目录 前言4 Kafka基准测试4.1 基于1个分区1个副本的基准测试4.2 基于3个分区1个副本的基准测试4.3 基于1个分区3个副本的基准测试 5 Java编程操作Kafka5.1 引入依赖5.2 向Kafka发送消息5.3 从Kafka消费消息5.4 异步使用带有回调函数的生产消息 6 幂等性6.1 幂等性介绍6.2 K…...

结合vueuse实现图片懒加载
介绍 为什么要有懒加载? 在一个网页中如果有很多张图片,那么用户初进这个页面的时候不必一次性把所有图片都加载出来,否则容易造成卡顿和浪费。应该是,用户的视图页面滑到该图片的位置,然后再把该图片加载出来。 前置…...

Mysql数据库--聚合查询、分组查询、联合查询(不同的连接方式)
文章目录 1.查询的进阶版1.1查询搭配插入进行使用1.2聚合查询1.3group by分组查询1.4联合查询之笛卡尔积1.5左外连接,右外连接介绍join on1.6自连表 1.查询的进阶版 1.1查询搭配插入进行使用 我们首先创建两张表,一个叫做student,一个叫做student2,两个…...
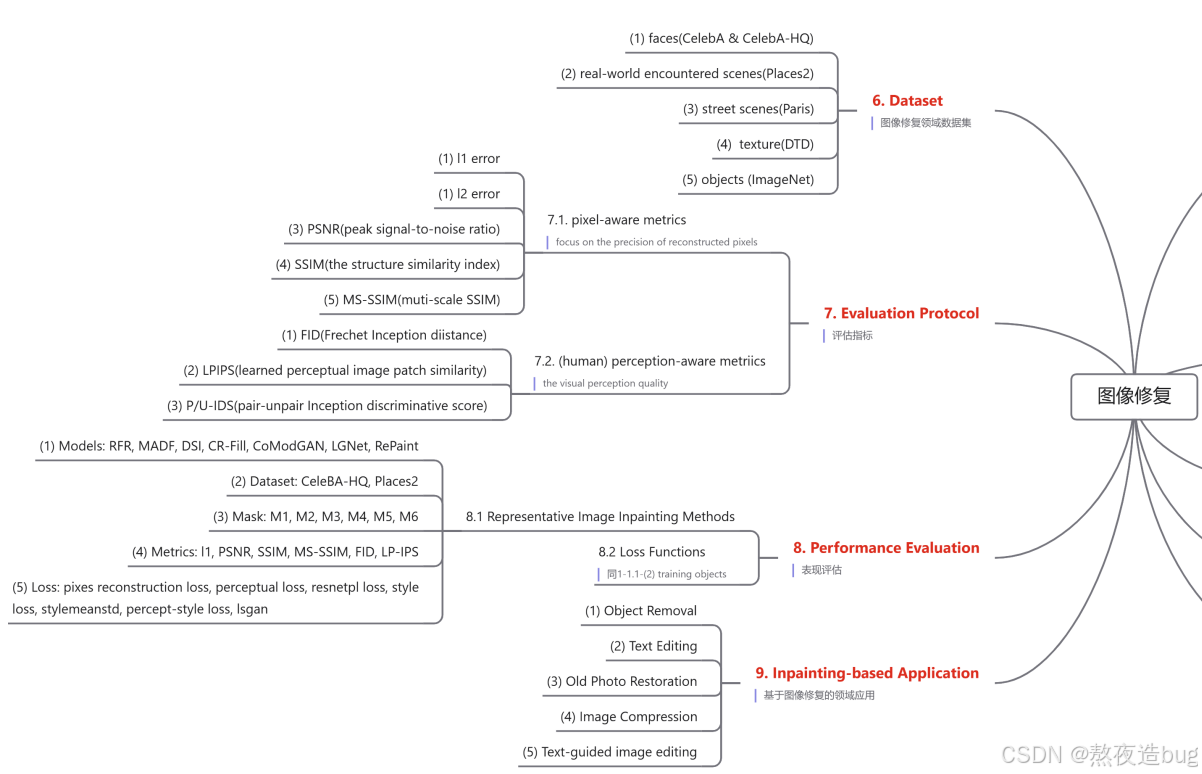
计算机视觉——图像修复综述篇
目录 1. Deterministic Image Inpainting 判别器图像修复 1.1. sigle-shot framework (1) Generators (2) training objects / Loss Functions 1.2. two-stage framework 2. Stochastic Image Inpainting 随机图像修复 2.1. VAE-based methods 2.2. GAN-based methods …...

集中式架构和分布式架构
数据是企业的核心资产和战略资源。面对爆炸性的数据增长,如何有效地组织、管理和利用数据成为企业的重大挑战。数据架构作为企业数据管理的蓝图和框架,发挥重要作用。本文就来详细说下当下主流的两种数据架构的类型。 首先明确数据架构定义:…...

Redis: 集群高可用之故障转移和集群迁移
故障转移 故障转移,包括自动故障转移和手动故障转移 1 )自动故障转移 Redis 集群,主节点挂了,从节点可以顶上来继续提供服务常用制造故障的两种方式 第一,对其中一个节点进行 SHUTDOWN 操作第二,kill 掉…...

记账软件在线、会计记账网站、财务记账官网、记账云、云记账、在线免费做账以及易舟云财务软件
记账软件在线、会计记账网站、财务记账官网、记账云、云记账、在线免费做账以及易舟云财务软件,以下是一些详细的介绍和推荐: 一、记账软件在线与会计记账网站 记账软件和会计记账网站是现代财务管理中不可或缺的工具,它们能够帮助企业或个人…...

Elasticsearch基础_3.基础操作
文章目录 一、索引操作1.1、创建索引1.2、删除索引 二、映射操作2.1、查看映射2.2、扩展映射 三、文档操作3.1、单条写入文档3.2、更新单条文档3.3、查看单条文档3.4、删除单条文档3.5、根据条件删除文档 一、索引操作 1.1、创建索引 PUT /${index_name} {"settings&quo…...

PHP永久性Cookie的含义
PHP中的永久性Cookie(也称为持久性Cookie)是指在用户的计算机上存储的一种持久性的HTTP Cookie。与常规的临时Cookie不同,永久性Cookie在浏览器关闭后依然保留,并且可以在用户下次访问该网站时被读取和使用。 主要特点 持久存储…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
