【蓝桥杯集训·每日一题】 AcWing 3996. 涂色
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- 区间DP
- Unique函数
一、题目
1、原题链接
3996. 涂色
2、题目描述
有 n 个砖块排成一排,从左到右编号为 1∼n。
其中,第 i 个砖块的初始颜色为 ci。
我们规定,如果编号范围 [i,j] 内的所有砖块的颜色都相同,且当第 i−1 和 第 j+1 个砖块存在时,这两个砖块的颜色和区间 [i,j] 的颜色均不同, 则砖块 i 和 j 属于同一个连通块。
例如,[3,3,3] 有 1 个连通块,[5,2,4,4] 有 3 个连通块。
现在,要对砖块进行涂色操作。
开始所有操作之前,你需要任选一个砖块作为起始砖块。
每次操作:
- 任选一种颜色。
- 将最开始选定的起始砖块所在连通块中包含的所有砖块都涂为选定颜色,
请问,至少需要多少次操作,才能使所有砖块都具有同一种颜色。
输入格式
第一行包含整数 n。
第二行包含 n 个整数 c1,c2,…,cn。
输出格式
一个整数,表示所需要的最少操作次数。
数据范围
前六个测试点满足,1≤n≤20。
所有测试点满足,1≤n≤5000,1≤ci≤5000。输入样例1:
4 5 2 2 1输出样例1:
2输入样例2:
8 4 5 2 2 1 3 5 5输出样例2:
4输入样例3:
1 4输出样例3:
0输入样例4:
5 1 3 1 2 1输出样例4:
3样例4解释
注意,每次染色操作所涉及的连通块必须包含所有操作开始前选定的起始砖块。
因此,答案是 3,而不是 2。
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总yyds
(1)因为每次都是改变起始点所在的连通块,所以颜色相同的砖块一定是一起改变的,所以我们可以先将原序列中颜色相同的砖块简化成一个砖块。
(2)
-
dp[i][j]表示所有在[i,j]中选择起点,并且将[i,j]的所有砖块染成同一种颜色的所有方案数中的最小操作次数。 -
根据第
i个砖块和第j个砖块颜色是否相同进行划分:①第
i个砖块和第j个砖块颜色不同:- 最后染色的为
i:即先求出[i+1,j]染成相同颜色的最小操作次数即dp[i+1][j],再加一次即将i染成与[i+1,j]相同的颜色,最小操作次数即为dp[i+1][j]+1。 - 最后染色的砖块为
j:同理,最小操作次数为dp[i][j-1]+1。
②第
i个砖块和第j个砖块颜色相同:- 先将
[i,j-2]染成相同颜色,再将j-1和[i,j-2]染成相同颜色,最后将j和[i,j-1]染成相同颜色:由于该方案是在dp[i][j-1]中的某些方案,也就是其子集,所以将[i,j-1]染成相同颜色的操作数是大于等于dp[i][j-1]。即总操作次数大于等于dp[i][j-1]+1。 - 先将
[i+1,j-1]染成相同颜色,再将i和[i+1,j-1]染成相同颜色,最后将j和[i,j-1]染成相同颜色(即i,j最后染色):即总操作次数为dp[i+1][j-1]+1。 - 由于第二种情况操作的区间比第一种情况操作的区间要短,所以可知,上述两种情况的最小操作次数为
dp[i+1][j-1]+1。
- 最后染色的为
-
综合上面三种情况,即第
i个砖块和第j个砖块颜色不同时dp[i][j]=min(dp[i+1][j]+1,dp[i][j-1]+1,否则第i个砖块和第j个砖块颜色相同时,dp[i][j]=dp[i+1][j-1]+1。
(3)利用上述思路,输出dp[1][n]即为答案。
2、时间复杂度
时间复杂度为O(n2)
3、代码详解
#include <iostream>
#include <algorithm>
using namespace std;
const int N=5010;
int c[N],dp[N][N];
int n;
int main(){cin>>n;for(int i=1;i<=n;i++) cin>>c[i];n=unique(c+1,c+n+1)-(c+1); //对数组去重,即合并颜色相同的砖块//枚举所有可能的区间长度for(int len=2;len<=n;len++){for(int i=1;i+len-1<=n;i++){int j=i+len-1;//i和j颜色不同时的转移方程if(c[i]!=c[j]) dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1;//i和j颜色相同时的转移方程else dp[i][j]=dp[i+1][j-1]+1;}}cout<<dp[1][n];return 0;
}
三、知识风暴
区间DP
Unique函数
- 在头文件
#include <algorithm>中包含。- 作用:对数组的相邻重复元素去重,并返回去重之后数组的尾地址(一般用
unique的返回值减去数组的首地址来求去重后数组的元素个数),如果重复元素不相邻的话一般要先对原数组进行排序操作。
相关文章:

【蓝桥杯集训·每日一题】 AcWing 3996. 涂色
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴区间DPUnique函数一、题目 1、原题链接 3996. 涂色 2、题目描述 有 n 个砖块排成一排,从左到右编号为 1∼n。 其中,第 i 个砖块的初始颜色为 ci。 …...

人工智能中的Web端编程
Java是当前的主流编程语言之一,常年稳居TIOBE编程语言排行榜前五。Java的使用领域非常广泛,包括了桌面端编程、Web端编程、移动端编程等几乎所有的编程领域。Java是Web端编程使用最广泛的编程语言之一。要学习Web端编程,需要了解Java语言的知…...
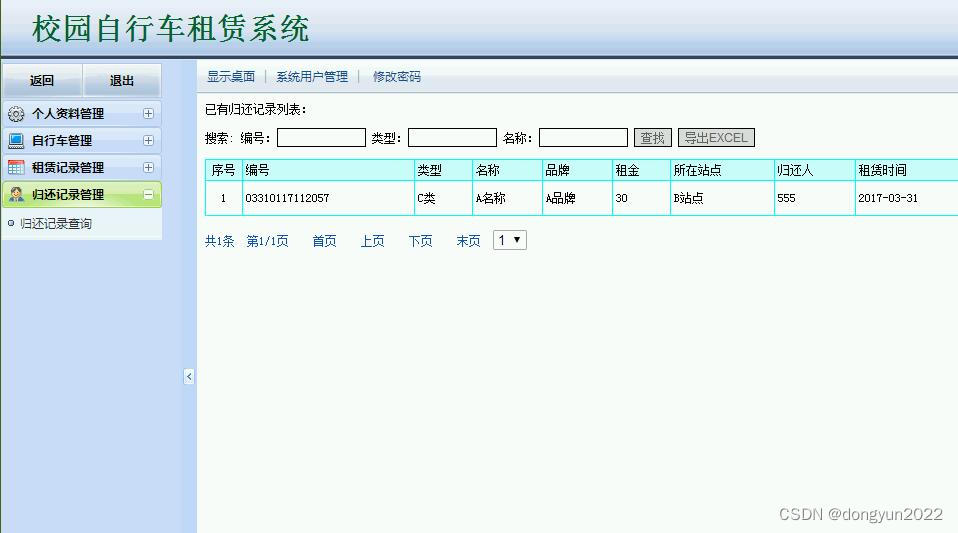
jsp+mysql+J2EE校园自行车租赁系统cdA1A2程序
本系统的具体功能有以下六项: 1、用户信息管理模块:用户需要注册成为本网站的用户,同时修改自己的用户资料,在必要时修改自己的登陆密码。 2、车辆查询模块:用户可以根据自己的要求,按照不同的查询方式来查询自己想要的…...

当营养遇上肠道菌群:探究其对儿童健康的影响
谷禾健康 越来越多的证据表明,肠道菌群定植紊乱和微生物多样性减少与全球非传染性疾病 (NCD) 的增加有关。影响儿童和青少年的非传染性疾病包括肥胖及其相关合并症、自身免疫性疾病、过敏性疾病和哮喘。饮食变化也与非传染性疾病的发病机制有关,并且由于…...

vue尚品汇商城项目-day01【4.完成非路由组件Header与Footer业务】
文章目录4.完成非路由组件Header与Footer业务4.1使用组件的步骤(非路由组件)本人其他相关文章链接4.完成非路由组件Header与Footer业务 在咱们项目开发中,不在以HTML CSS 为主,主要搞业务、逻辑 开发项目的流程: (1)…...

IDEA安装教程(图文详解,一步搞定)
文章目录第一步:官网下载IDEA第二步:卸载旧的IDEA(没有则跳过)第二步:安装IDEA第一步:官网下载IDEA 地址:https://www.jetbrains.com/idea/download/other.html 第二步:卸载旧的I…...

【01 DualCam Porting】
1、配置camera_custom_stero_setting.h a、增加sensor配置 /vendor/mediatek/proprietary/custom/mt6765/hal/camera/camera_custom_stereo_setting.h注意: 1)IMGOYUV Size:在有FOV crop的情况下,不能配置为sensor full size,建议比full size 小或者配置为fov crop的值…...

redis --- string类型的使用
目录 一、string类型使用 1.1、set key value参数解析 1.2、同时设置/获取多个键值 1.3、获取/设置指定区间范围内的值 1.4、数值增减 1.5、获取字符串长度和内容追加 1.6、分布式锁 1.7、getset(先get再set) 一、string类型使用 1.1、set key value参数解析 SET key v…...
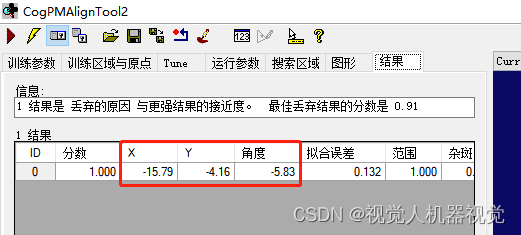
康耐视visionpro-机器视觉定位引导-经验总结-来自视觉人粉丝分享
1、机器人吸取电路板,移动到拍照位置,并在电路板上找一个标记点,并且,通过机器人示教把当前电路板能够准确的放入到目标位置。 2、机器人吸取电路板吸取电路板,在x,y方向进行移动,总共移动4个位置ÿ…...

包管理工具npm
一:package.json 在某个文件路径下,执行 npm init。就会生成package.json文件。大致如下: {"name": "test","version": "1.0.0","description": "测试","main": &q…...

ChatGPT正进军各行各业,抓住机遇,拥有无限的可能性。
每一个新技术的出现都会对各行各业产生冲击,但关键在于如何抓住这个机遇。ChatGPT是一项非常具有前途的技术,它可以在许多领域为人们提供更好的服务和体验。这项技术的优势之一是它可以快速而准确地理解和解释自然语言,从而使人们可以更轻松地…...
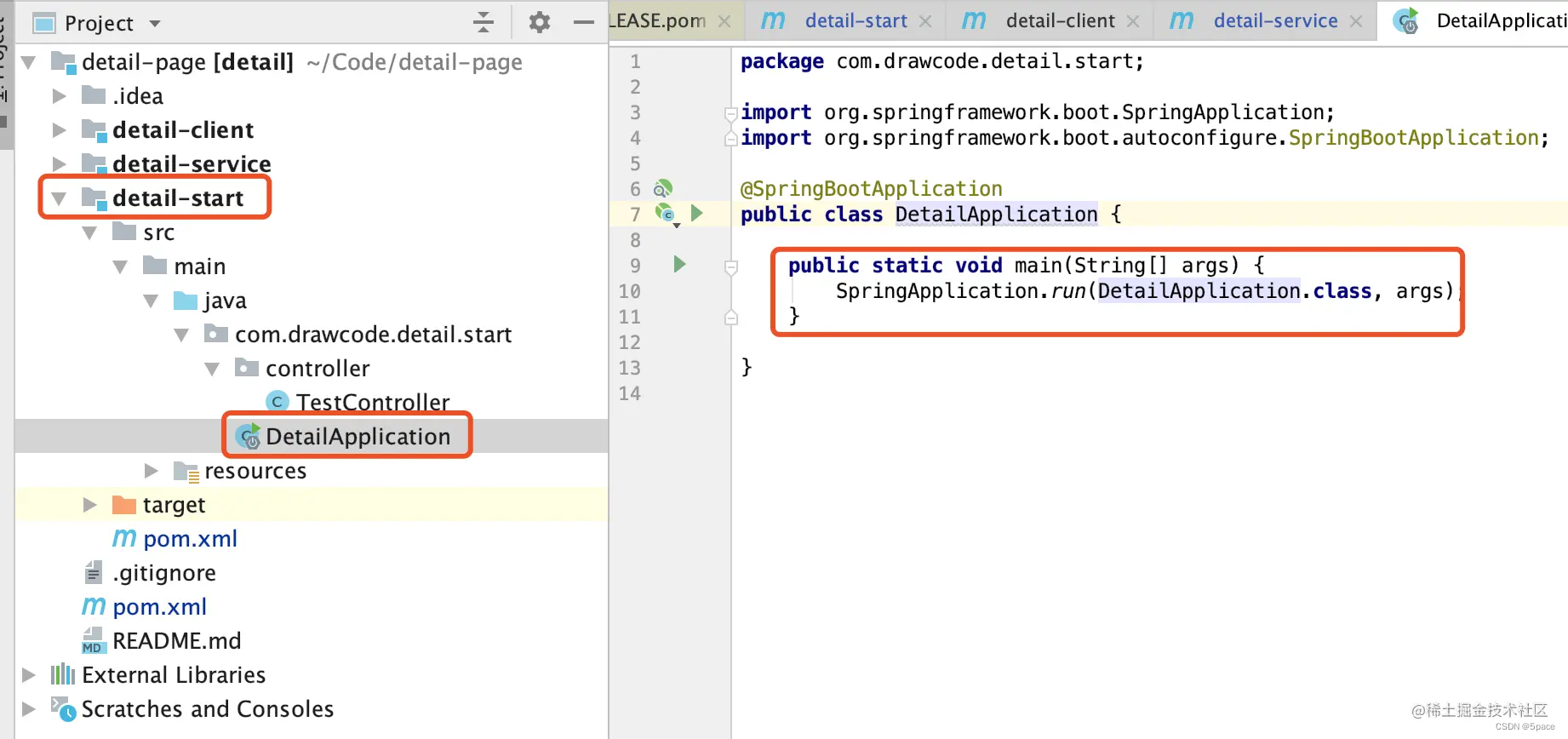
Maven 多模块管理
多模块管理简单地理解就是一个 Java 工程项目中不止有一个 pom.xml 文件,会在不同的目录中有多个这样的文件,进而实现 Maven 的多模块管理 在多人使用Maven协作开发项目时,尤其是稍微上点规模的项目,每个RD的工作都细分到具体功能…...

crash 内核调试工具 ps 指令 显示的进程状态 RU, IN, UN, ZO, ST, TR, DE, SW, WA, PA 什么意思
crash> help ps | grep "the task state" 5. the task state (RU, IN, UN, ZO ,ST, TR, DE, SW, WA, PA, ID, NE) 参考linux-4.19.113内核源码(include/linux/sched.h),有如下定义 /** Task state bitmask. NOTE! These bits…...

Spring《二》bean的实例化与生命周期
🍎道阻且长,行则将至。🍓 上一篇:Spring《一》快速入门 下一篇:Spring《三》DI依赖注入 目录一、bean实例化🍍1.构造方法 ***2.静态工厂 *使用工厂创建对象实例化bean3.实例工厂 ***使用示例工厂创建对象实…...

java与kotlin 写法区别
原文链接:https://gitcode.net/mirrors/mindorksopensource/from-java-to-kotlin?utm_sourcecsdn_github_accelerator#assigning-the-null-value Print to Console 打印到控制台 Java System.out.print("Amit Shekhar"); System.out.println("Amit…...

服务器运行深度学习代码使用指南
该内容配置均在九天毕昇下配置。 当前系统使用的linux版本为:Ubuntu 18.04 LTS。 当前版本安装的是:cuda10.1。 九天毕昇平台:https://jiutian.10086.cn/edu/#/home 一、linux下运行python的操作 ls 为列出当前目录中的文件 cd 文件名 进入…...
计算机组成原理 - 2. 数据的表示和运算
整理自天勤高分笔记,购书链接: 24 天勤高分笔记 要记住的几个数字 📓: 215327682^{15} 3276821532768 216655362^{16} 6553621665536 23121474836482^{31} 21474836482312147483648 23242949672962^{32} 4294967296232429496…...

【js】基础知识点--语句,break和continue,switch,with,for..in,do-while,while
一、break和continue语句,常用 break 语句会立即退出循环,强制继续执行循环后面的语句。而 continue 语句虽然也是立即退出循环,但退出循环后会从循环的顶部继续执行 var num 0; for (var i1; i < 10; i) {if (i % 5 0) {break;}num; …...
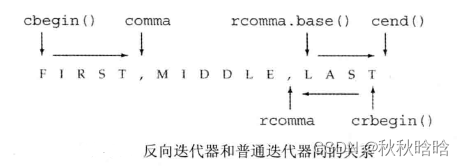
【C++】迭代器
内容来自《C Primer(第5版)》9.2.1 迭代器、9.2.3 begin和end成员、9.3.6 容器操作可能使迭代器失效、10.4.3 反向迭代器 目录 1. 迭代器 1.1 迭代器范围 1.2 使用左闭合范围蕴含的编程假定 2. begin和end成员 3. 容器操作可能使迭代器失效 3.1 编…...

数据可视化在前端中的应用
前端开发中,数据可视化是一种非常重要的技术。它可以将复杂的数据以图形化的方式展示出来,让用户更容易理解和分析数据。在前端中,VUE是一种非常流行的JavaScript框架,可以用来实现各种数据可视化效果。 首先,让我们来看看一些常见的数据可视化方式: 表格:表格是数据可…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
