图的遍历算法
图的遍历
- 1.连通图的深度优先搜索
- 1.1. 递归
- 1.2.非递归
- 2.连通图的广度优先遍历
- 3. 非连通图的深度(广度)优先遍历
1.连通图的深度优先搜索
算法思想:从图中某个顶点vi出发,访问此顶点,然后依次从v1的各个未被访问的邻接点出发进行深度优先搜索来遍历图,直至所有与v1所有路径想通的顶点都被访问到为止。
【算法描述】
- 访问顶点v
- 从v的未被访问的邻接点中选取一个顶点w,从w出发进行深度优先遍历,如此深入下去,当某个顶点的所有邻接点都被访问过时,返回上一层,继续上一层中未被访问的顶点进行深度优先遍历,直至图中所有和v有路径想通的顶点都被访问为止
1.1. 递归
【深度遍历递归】
//基于邻接矩阵的连通图的深度优先遍历递归算法
void df_traver_MGraph(const MGraph* G, int v, int visited[])
{//G的存储结构为矩阵,v为出发编号,标志数组已经初始化为0printf("%d ", G->vexs[v]);//访问出发结点visited[v] = 1;//做已访问标记for (int w = 0; w < G->vexNum; w++){//查找和结点v有邻接关系的结点wif (G->arcs[v][w] != 0 && visited[w] == 0)df_traver_MGraph(G, w, visited);}
}
//基于邻接表的连通图的深度优先遍历递归算法
void df_traver_ALGraph(const ALGraph* G, int v, int visited[])
{//G的存储结构为邻接表,v为出发点编号,标记数组已经初始化为0printf("%d ", G->adjlist[v].vertex);//访问出发结点visited[v] = 1;//做已访问标记ArcNode* p = G->adjlist[v].firstArc;//得到边链表的头指针while (p)//查找与v有邻接关系的邻接点{int w = p->adjvex;//w是v的邻接点if (visited[w] == 0)df_traver_ALGraph(G, w, visited);//递归调用p = p->nextArc;}
}
对于先访问的顶点,其深度优先遍历后结束;后访问的顶点,其深度优先遍历先结束。所以,深度优先遍历可以用栈的结构来进行非递归遍历。
关键:是要找进行深度优先遍历的下一个邻接结点的位置。
1.2.非递归
//基于邻接矩阵的连通图的深度优先遍历非递归算法
void df_traver_no_MGraph(const MGraph* G, int v)
{//MGraph是图的邻接矩阵数据类型,从顶点v出发,深度优先遍历连通图Gassert(G);Stack S; StackInit(&S);//创建栈int visited[20] = { 0 };//标记数组,判断结点是否被访问过//初始化标记数组for (int i = 0; i < 20; i++)visited[i] = 0;//访问出发标号为v的结点printf("%d ", G->vexs[v-1]);//设置标号为v的结点已经被访问visited[v] = 1;//出发结点进栈StackPush(&S, v);//寻找v的第一个邻接结点标号int w = FirstAdjVex_MGraph(G, v);while (!StackEmpty(&S))//栈为空的时候,说明所有结点访问{if (w != 0 && visited[w] == 0)//w存在且,标号为w的结点没有被访问过{printf("%d ", G->vexs[w - 1]);visited[w] = 1;StackPush(&S, w);//编号w进栈}else if(w==0)//栈顶出栈{if (StackEmpty(&S))break;v = StackTop(&S);StackPop(&S);w = FirstAdjVex_MGraph(G, v);continue;}w = NextAdjVex_MGraph(G, v, w);//找v的下一个邻接点编号}//销毁栈StackDestroy(&S);
}
/****************************************************/
//基于邻接表的连通图的深度优先遍历非递归算法
void df_traver_no_AlGraph(const ALGraph* G, int v)
{//ALGraph是图的邻接表数据类型,从顶点v出发,深度优先遍历连通图Gassert(G);Stack S; StackInit(&S);//创建栈int visited[20] = { 0 };//标记数组,判断结点是否被访问过//初始化标记数组for (int i = 0; i < 20; i++)visited[i] = 0;//访问出发标号为v的结点printf("%d ", G->adjlist[v-1].vertex);//设置标号为v的结点已经被访问visited[v] = 1;//出发结点进栈StackPush(&S, v);//寻找v的第一个邻接结点标号int w = FirstAdjVex_ALGraph(G, v);while (!StackEmpty(&S))//栈为空的时候,说明所有结点访问{if (w != 0 && visited[w] == 0)//w存在且,标号为w的结点没有被访问过{printf("%d ", G->adjlist[w - 1].vertex);visited[w] = 1;StackPush(&S, w);//编号w进栈}else if (w == 0)//栈顶出栈{if (StackEmpty(&S))break;v = StackTop(&S);StackPop(&S);w = FirstAdjVex_ALGraph(G, v);continue;}w = NextAdjVex_ALGraph(G, v, w);//找v的下一个邻接点编号}//销毁栈StackDestroy(&S);
}//基于领接矩阵,寻找顶点v第一个领接顶点w标号
int FirstAdjVex_MGraph(const MGraph* G, int v)
{assert(G);int j = 0;for (j = 0; j < G->vexNum; j++){if (G->arcs[v - 1][j] != 0)//坐标为第一个非0,说明顶点v和j+1的顶点有联系return j + 1;//返回第一个与顶点v有联系的邻接结点编号,下标+1}return 0;//不存在则返回0
}
//基于邻接矩阵,寻找顶点v的下一个邻接顶点编号
int NextAdjVex_MGraph(const MGraph* G, int v, int w)
{assert(G);int j = 0;for (j = w; j < G->vexNum; j++)//从一个邻接结点编号的下一个编号开始寻找{if (G->arcs[v - 1][j] != 0)//坐标为下一个非0,说明顶点v和j+1的顶点有联系return j + 1;//返回第一个与顶点v有联系的邻接结点编号,下标+1}return 0;//不存在则返回0
}
//基于邻接表,寻找顶点v第一个领接顶点w
int FirstAdjVex_ALGraph(const ALGraph* G, int v)
{assert(G);if (G->adjlist[v - 1].firstArc != NULL){return G->adjlist[v - 1].firstArc->adjvex+1;}return 0;
}
//基于邻接表,寻找顶点v的下一个邻接顶点编号
int NextAdjVex_ALGraph(const ALGraph* G, int v, int w)
{assert(G);ArcNode* p = G->adjlist[v - 1].firstArc;while (p){if (p->adjvex + 1 == w)//找到存放编号为w的边结点break;p = p->nextArc;}if (!p || !p->nextArc)return 0;//没有找到w的下一个邻结点编号else{return p->nextArc->adjvex;}
}
2.连通图的广度优先遍历
算法思想:从图中的某个顶点出发,访问此顶点之后,依次访问v的所有未被访问过的邻接点,之后按这些顶点被访问的先后依次访问它们的邻接结点。
【算法描述】
- 访问初始顶点,并将其顶点编号入队列。
- 队列不为空,则队头顶点编号出队列;依次访问它的每一个未访问过的邻接点,并将其顶点编号入队列。
- 重复2,直至队列为空,遍历结束。
【算法实现】
//基于邻接矩阵的连通图的广度优先遍历算法
void bf_traver_MGraph(const MGraph* G, int v)
{int visited[10] = { 0 };//队列Q存放已经访问过的顶点编号,v为出发点编号Queue Q; QueueInit(&Q);//访问出发结点,将出发结点编号进队列printf("%d ", G->vexs[v - 1]);visited[v] = 1;QueuePush(&Q, v);while (!QueueEmpty(&Q)){int u = QueueFront(&Q); QueuePop(&Q);for (int w = 0; w < G->vexNum; w++)//找出u的所有邻接结点{if (G->arcs[u - 1][w] != 0 && visited[w+1] == 0){printf("%d ", G->vexs[w]);visited[w+1] = 1;QueuePush(&Q, w);}}}
}
//基于邻表的连通图的广度优先遍历算法
void bf_traver_ALGraph(const ALGraph* G, int v)
{int visited[10] = { 0 };//队列Q存放已经访问过的顶点编号,v为出发点编号Queue Q; QueueInit(&Q);//访问出发结点,将出发结点编号进队列printf("%d ", G->adjlist[v - 1].vertex);visited[v] = 1;QueuePush(&Q, v);while (!QueueEmpty(&Q)){int u = QueueFront(&Q); QueuePop(&Q);ArcNode* p = G->adjlist[u - 1].firstArc;while (p != NULL)//找出u的所有邻接点{int w = p->adjvex;//取邻接点编号if (visited[w + 1] == 0){printf("%d ", G->adjlist[w].vertex);visited[w + 1] = 1;QueuePush(&Q, w + 1);}p = p->nextArc;}}
}
3. 非连通图的深度(广度)优先遍历
对每一个未被访问过的顶点进行深度(广度)优先遍历
【算法实现】
//非连通图的深度(广度)优先遍历
void traver(const MGraph* G)
{assert(G);int visited[10] = { 0 };for (int i = 0; i < G->vexNum; i++){if (visited[i] == 0)df_traver_MGraph(G, i, visited);//深度//bf_traver_MGraph(&G, i + 1);广度}
}
相关文章:

图的遍历算法
图的遍历1.连通图的深度优先搜索1.1. 递归1.2.非递归2.连通图的广度优先遍历3. 非连通图的深度(广度)优先遍历1.连通图的深度优先搜索 算法思想:从图中某个顶点vi出发,访问此顶点,然后依次从v1的各个未被访问的邻接点…...

【蓝桥杯集训·每日一题】 AcWing 3996. 涂色
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴区间DPUnique函数一、题目 1、原题链接 3996. 涂色 2、题目描述 有 n 个砖块排成一排,从左到右编号为 1∼n。 其中,第 i 个砖块的初始颜色为 ci。 …...

人工智能中的Web端编程
Java是当前的主流编程语言之一,常年稳居TIOBE编程语言排行榜前五。Java的使用领域非常广泛,包括了桌面端编程、Web端编程、移动端编程等几乎所有的编程领域。Java是Web端编程使用最广泛的编程语言之一。要学习Web端编程,需要了解Java语言的知…...
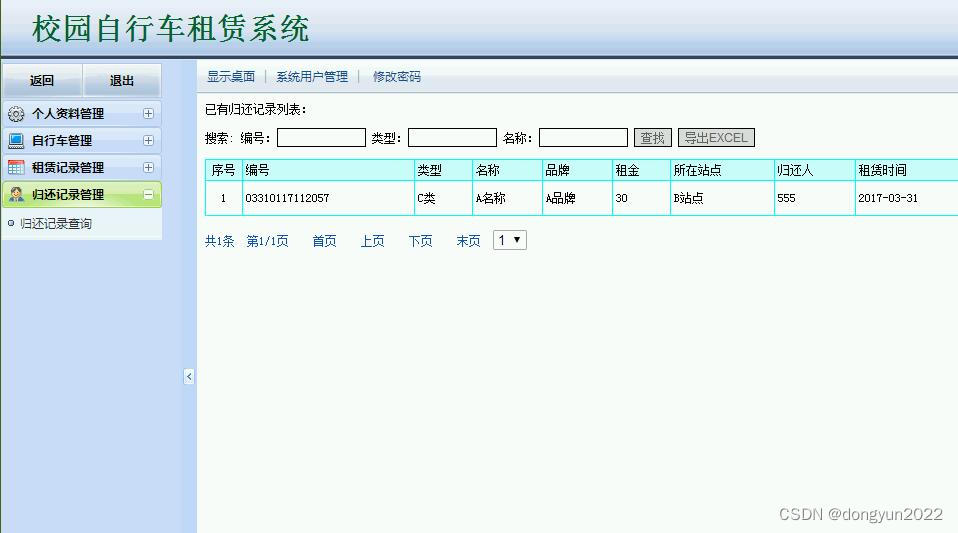
jsp+mysql+J2EE校园自行车租赁系统cdA1A2程序
本系统的具体功能有以下六项: 1、用户信息管理模块:用户需要注册成为本网站的用户,同时修改自己的用户资料,在必要时修改自己的登陆密码。 2、车辆查询模块:用户可以根据自己的要求,按照不同的查询方式来查询自己想要的…...

当营养遇上肠道菌群:探究其对儿童健康的影响
谷禾健康 越来越多的证据表明,肠道菌群定植紊乱和微生物多样性减少与全球非传染性疾病 (NCD) 的增加有关。影响儿童和青少年的非传染性疾病包括肥胖及其相关合并症、自身免疫性疾病、过敏性疾病和哮喘。饮食变化也与非传染性疾病的发病机制有关,并且由于…...

vue尚品汇商城项目-day01【4.完成非路由组件Header与Footer业务】
文章目录4.完成非路由组件Header与Footer业务4.1使用组件的步骤(非路由组件)本人其他相关文章链接4.完成非路由组件Header与Footer业务 在咱们项目开发中,不在以HTML CSS 为主,主要搞业务、逻辑 开发项目的流程: (1)…...

IDEA安装教程(图文详解,一步搞定)
文章目录第一步:官网下载IDEA第二步:卸载旧的IDEA(没有则跳过)第二步:安装IDEA第一步:官网下载IDEA 地址:https://www.jetbrains.com/idea/download/other.html 第二步:卸载旧的I…...

【01 DualCam Porting】
1、配置camera_custom_stero_setting.h a、增加sensor配置 /vendor/mediatek/proprietary/custom/mt6765/hal/camera/camera_custom_stereo_setting.h注意: 1)IMGOYUV Size:在有FOV crop的情况下,不能配置为sensor full size,建议比full size 小或者配置为fov crop的值…...

redis --- string类型的使用
目录 一、string类型使用 1.1、set key value参数解析 1.2、同时设置/获取多个键值 1.3、获取/设置指定区间范围内的值 1.4、数值增减 1.5、获取字符串长度和内容追加 1.6、分布式锁 1.7、getset(先get再set) 一、string类型使用 1.1、set key value参数解析 SET key v…...
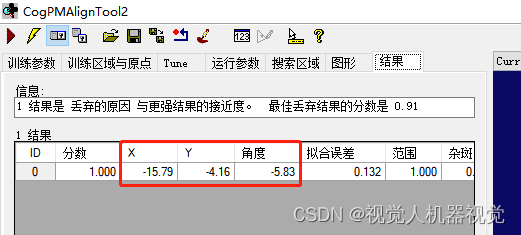
康耐视visionpro-机器视觉定位引导-经验总结-来自视觉人粉丝分享
1、机器人吸取电路板,移动到拍照位置,并在电路板上找一个标记点,并且,通过机器人示教把当前电路板能够准确的放入到目标位置。 2、机器人吸取电路板吸取电路板,在x,y方向进行移动,总共移动4个位置ÿ…...

包管理工具npm
一:package.json 在某个文件路径下,执行 npm init。就会生成package.json文件。大致如下: {"name": "test","version": "1.0.0","description": "测试","main": &q…...

ChatGPT正进军各行各业,抓住机遇,拥有无限的可能性。
每一个新技术的出现都会对各行各业产生冲击,但关键在于如何抓住这个机遇。ChatGPT是一项非常具有前途的技术,它可以在许多领域为人们提供更好的服务和体验。这项技术的优势之一是它可以快速而准确地理解和解释自然语言,从而使人们可以更轻松地…...
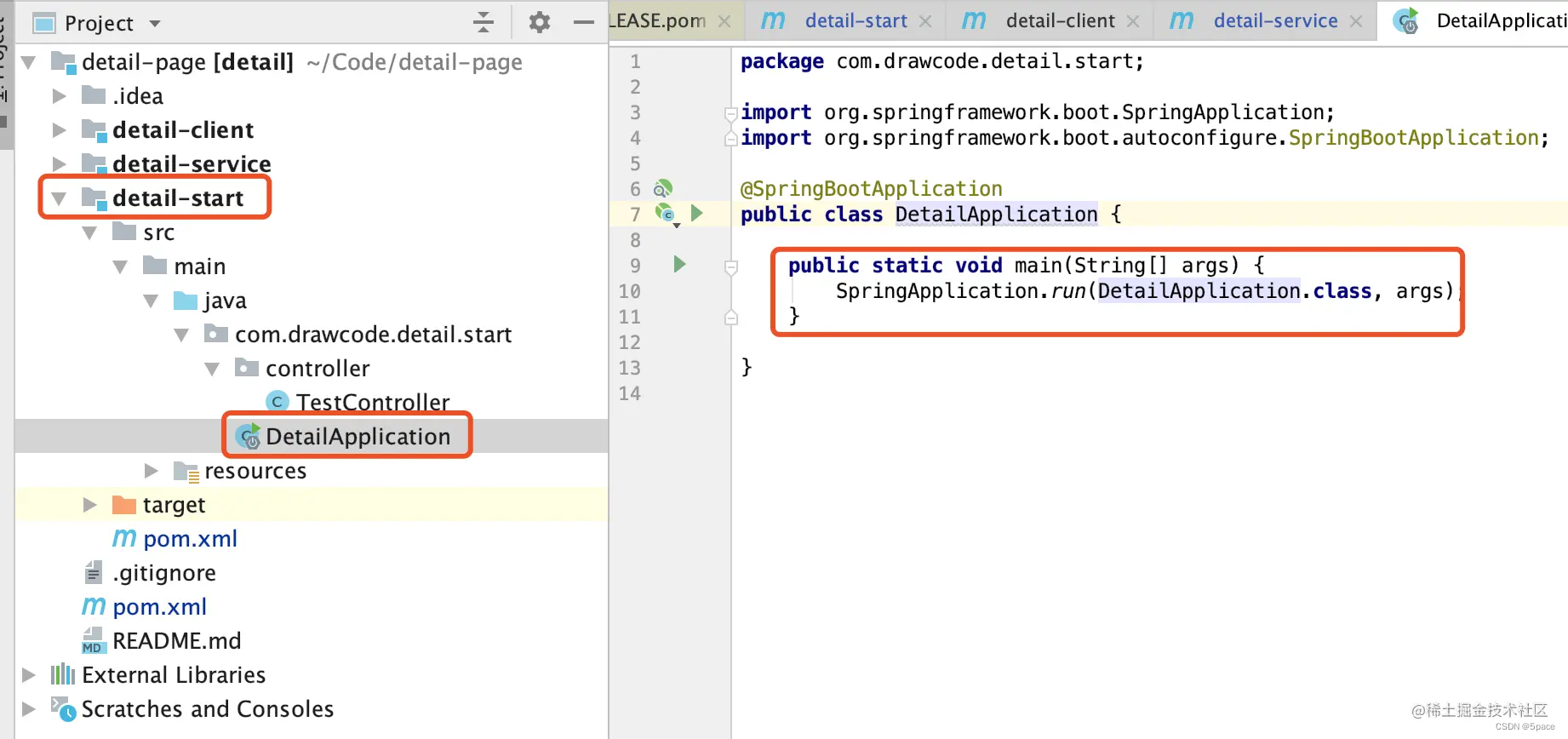
Maven 多模块管理
多模块管理简单地理解就是一个 Java 工程项目中不止有一个 pom.xml 文件,会在不同的目录中有多个这样的文件,进而实现 Maven 的多模块管理 在多人使用Maven协作开发项目时,尤其是稍微上点规模的项目,每个RD的工作都细分到具体功能…...

crash 内核调试工具 ps 指令 显示的进程状态 RU, IN, UN, ZO, ST, TR, DE, SW, WA, PA 什么意思
crash> help ps | grep "the task state" 5. the task state (RU, IN, UN, ZO ,ST, TR, DE, SW, WA, PA, ID, NE) 参考linux-4.19.113内核源码(include/linux/sched.h),有如下定义 /** Task state bitmask. NOTE! These bits…...

Spring《二》bean的实例化与生命周期
🍎道阻且长,行则将至。🍓 上一篇:Spring《一》快速入门 下一篇:Spring《三》DI依赖注入 目录一、bean实例化🍍1.构造方法 ***2.静态工厂 *使用工厂创建对象实例化bean3.实例工厂 ***使用示例工厂创建对象实…...

java与kotlin 写法区别
原文链接:https://gitcode.net/mirrors/mindorksopensource/from-java-to-kotlin?utm_sourcecsdn_github_accelerator#assigning-the-null-value Print to Console 打印到控制台 Java System.out.print("Amit Shekhar"); System.out.println("Amit…...

服务器运行深度学习代码使用指南
该内容配置均在九天毕昇下配置。 当前系统使用的linux版本为:Ubuntu 18.04 LTS。 当前版本安装的是:cuda10.1。 九天毕昇平台:https://jiutian.10086.cn/edu/#/home 一、linux下运行python的操作 ls 为列出当前目录中的文件 cd 文件名 进入…...
计算机组成原理 - 2. 数据的表示和运算
整理自天勤高分笔记,购书链接: 24 天勤高分笔记 要记住的几个数字 📓: 215327682^{15} 3276821532768 216655362^{16} 6553621665536 23121474836482^{31} 21474836482312147483648 23242949672962^{32} 4294967296232429496…...

【js】基础知识点--语句,break和continue,switch,with,for..in,do-while,while
一、break和continue语句,常用 break 语句会立即退出循环,强制继续执行循环后面的语句。而 continue 语句虽然也是立即退出循环,但退出循环后会从循环的顶部继续执行 var num 0; for (var i1; i < 10; i) {if (i % 5 0) {break;}num; …...
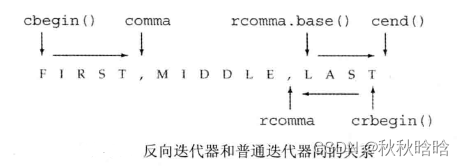
【C++】迭代器
内容来自《C Primer(第5版)》9.2.1 迭代器、9.2.3 begin和end成员、9.3.6 容器操作可能使迭代器失效、10.4.3 反向迭代器 目录 1. 迭代器 1.1 迭代器范围 1.2 使用左闭合范围蕴含的编程假定 2. begin和end成员 3. 容器操作可能使迭代器失效 3.1 编…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
