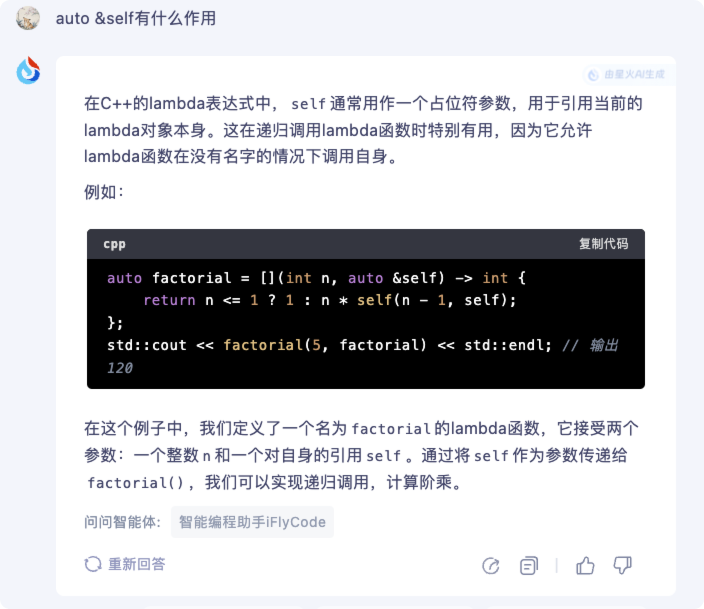
atcoder-374(a-e)
atcoder-374
文章目录
- atcoder-374
- A
- B
- C
- 简洁的写法
- 正解
- D
- 正解
- E
A
#include<bits/stdc++.h>using namespace std;signed main()
{string s;cin>>s;string str=s.substr(s.size()-3);if(str =="san") puts("Yes");else puts("No");return 0;
}
B
#include<bits/stdc++.h>using namespace std;signed main()
{string s,t;cin>>s>>t;int slen=s.size();int tlen=t.size();if(slen>tlen){swap(s,t);swap(slen,tlen);}int flag=1;if(s==t) puts("0");else{for(int i=0;i<s.size();i++){if(s[i]!=t[i]){cout<<i+1<<endl;flag=0;return 0;}}if(flag&&tlen!=slen){cout<<slen+1<<endl;}}return 0;
}
C
#include<bits/stdc++.h>using namespace std;signed main()
{int n;cin>>n;vector<int> k(n);int ans=0;for(int i=0;i<n;i++){cin>>k[i];ans+=k[i];}sort(k.begin(),k.end());int mid=0;for(int i=0;i<n;i++){mid+=k[i];if(mid>=ans/2){break;}}cout<<mid<<endl;return 0;
}
找到离中间值最近的组合
n最大也就20,搜索算法即可
#include<bits/stdc++.h>using namespace std;
typedef long long ll;
const int N=25;
ll k[N];
int v[N];
int n;
ll ans=0;
ll res=1e18;void dfs(int u,ll cnt)
{if(cnt<=res&&cnt>=ans/2ll){res=cnt;}for(int i=1;i<n;i++){if(!v[i]){v[i]=1;dfs(i,cnt+k[i]);v[i]=0;}}
}signed main()
{cin>>n;for(int i=0;i<n;i++){cin>>k[i];ans+=k[i];}
// cout<<ans<<endl;dfs(0,0ll);cout<<res<<endl;return 0;
}
为什么正着做不行
#include<bits/stdc++.h>using namespace std;
typedef long long ll;
const int N=25;
ll k[N];
int v[N];
int n;
ll ans=0;
ll res=0;void dfs(int u,ll cnt)
{if(cnt<=ans/2ll&&res<=cnt){res=cnt;}for(int i=u;i<n;i++){if(!v[i]){v[i]=1;dfs(i,cnt+k[i]);v[i]=0;}}
}signed main()
{cin>>n;for(int i=0;i<n;i++){cin>>k[i];ans+=k[i];}
// cout<<ans<<endl;dfs(0,0);cout<<ans-res<<endl;return 0;
}
简洁的写法
因为N最大为20,2的20次方也就1e6的复杂度,那直接暴力枚举就可以求解
但是用二进制表示选或者不选,怎么去做判断呢
#include<bits/stdc++.h>using namespace std;signed main()
{int n;cin>>n;vector<int> a(n+1);for(int i=1;i<=n;i++) cin>>a[i];int ans=0;for(int i=0;i< (1<<n+1);i++){int s = i;for(int j=0;j<32;j++){if(i>>j&1) ans+=a[i];}if(ans) }return 0;
}
正解
jianly的状态求和有点像前缀和
#include<bits/stdc++.h>using namespace std;signed main()
{int n;cin>>n;vector<int> k(n+1);for(int i=1;i<=n;i++) cin>>k[i];int tot = accumulate(k.begin()+1,k.end(),0);
// cout<<tot<<endl;vector<int> sum(1<<n);int ans=1e9;for(int i=0; i<(1<<n); i++){if(i>0){int u = __builtin_ctz(i);sum[i]=k[u]+sum[i^(1<<u)];}ans = min(ans,max(sum[i],tot-sum[i]));}cout<<ans<<endl;return 0;
}
D
那两条线近就先走哪两段
就是最短路
其实是最小生成树
#include<bits/stdc++.h>using namespace std;signed main()
{ios::sync_with_stdio(false);cin.tie(0);int n,s,t;cin>>n>>s>>t;vector<int> a(n+1),b(n+1),c(n+1),d(n+1);vector<bool> v(n+1);for(int i=1;i<=n;i++) cin>>a[i]>>b[i]>>c[i]>>d[i];double res=1e9;auto dfs = [&](auto &self,int x,int y,double ans=0.0,int cnt=0){if(cnt==n){res=min(ans,res);return ;}for(int i=1;i<=n;i++){if(v[i]) continue;double dis0=hypot(a[i]-x,b[i]-y);double dis1=hypot(c[i]-x,b[i]-y);double dis =hypot(a[i]-c[i],b[i]-d[i]);cout<<dis<<endl;v[i]=1;self(self,a[i],b[i],ans+dis,cnt+1);self(self,c[i],d[i],ans+dis,cnt+1);v[i]=0;}};dfs(dfs,0,0);return 0;
}
现在需要解决的是,如何输出样例那么长的小数,以及当两条线段重合时的距离需要重新计算
#include<bits/stdc++.h>using namespace std;
typedef long long ll;
const int N=10,M=2*N;
int pa[N];
int n;
double s,t;struct xian{int a,b;int c,d;double dis=0;
}xs[N];struct node{int a,b;double dis;bool operator<(const node &M)const{return dis<M.dis;}
}ns[M];double dist(double x,double y,double xx,double yy){return sqrt((x-xx)*(x-xx)+(y-yy)*(y-yy));
}int find(int x){if(x!=pa[x]) pa[x]=find(pa[x]);return pa[x];
}signed main()
{cin>>n>>s>>t;double ans=0;for(int i=1;i<=n;i++){cin>>xs[i].a>>xs[i].b>>xs[i].c>>xs[i].d;xs[i].dis=dist(xs[i].a,xs[i].b,xs[i].c,xs[i].d);ans+=xs[i].dis/t;// cout<<xs[i].a<<' '<<xs[i].b<<' '<<xs[i].c<<' '<<xs[i].d<<' '<<xs[i].dis<<endl;}
// cout<<ans<<endl;int cnt=1;for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){auto &u=xs[i],&v=xs[j];double dis=1e9;dis=min(dist(u.a,u.b,v.a,v.b),dis);dis=min(dist(u.a,u.b,v.c,v.d),dis);dis=min(dist(u.c,u.d,v.a,v.b),dis);dis=min(dist(u.c,u.d,v.c,v.d),dis);ns[cnt++]={i,j,dis};}}sort(ns+1,ns+cnt+1);for(int i=1;i<=n;i++) pa[i]=i;for(int i=1;i<=cnt;i++){int a=ns[i].a;int b=ns[i].b;double dis=ns[i].dis;a=find(a),b=find(b);if(a!=b){// cout<<a<<' '<<b<<' '<<dis<<endl; pa[a]=b;ans+=dis/s;}}printf("%lf",ans);return 0;
}
#include<bits/stdc++.h>using namespace std;
typedef long long ll;
const int N=10,M=2*N;
int pa[N];
int n;
double s,t;struct xian{int a,b;int c,d;double dis=0;
}xs[N];struct node{int a,b;double dis;bool operator<(const node &M)const{return dis<M.dis;}
}ns[M];double dist(double x,double y,double xx,double yy){return sqrt((x-xx)*(x-xx)+(y-yy)*(y-yy));
}int find(int x){if(x!=pa[x]) pa[x]=find(pa[x]);return pa[x];
}signed main()
{cin>>n>>s>>t;double ans=0;for(int i=1;i<=n;i++){cin>>xs[i].a>>xs[i].b>>xs[i].c>>xs[i].d;xs[i].dis=dist(xs[i].a,xs[i].b,xs[i].c,xs[i].d);ans+=xs[i].dis/t;// cout<<xs[i].a<<' '<<xs[i].b<<' '<<xs[i].c<<' '<<xs[i].d<<' '<<xs[i].dis<<endl;}
// cout<<ans<<endl;int cnt=1;for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){auto &u=xs[i],&v=xs[j];double dis=1e9;dis=min(dist(u.a,u.b,v.a,v.b),dis);dis=min(dist(u.a,u.b,v.c,v.d),dis);dis=min(dist(u.c,u.d,v.a,v.b),dis);dis=min(dist(u.c,u.d,v.c,v.d),dis);ns[cnt++]={i,j,dis};}}sort(ns+1,ns+cnt+1);for(int i=1;i<=n;i++) pa[i]=i;for(int i=1;i<=cnt;i++){int a=ns[i].a;int b=ns[i].b;double dis=ns[i].dis;a=find(a),b=find(b);if(a!=b){// cout<<a<<' '<<b<<' '<<dis<<endl; pa[a]=b;ans+=dis/s;}}printf("%lf",ans);return 0;
}

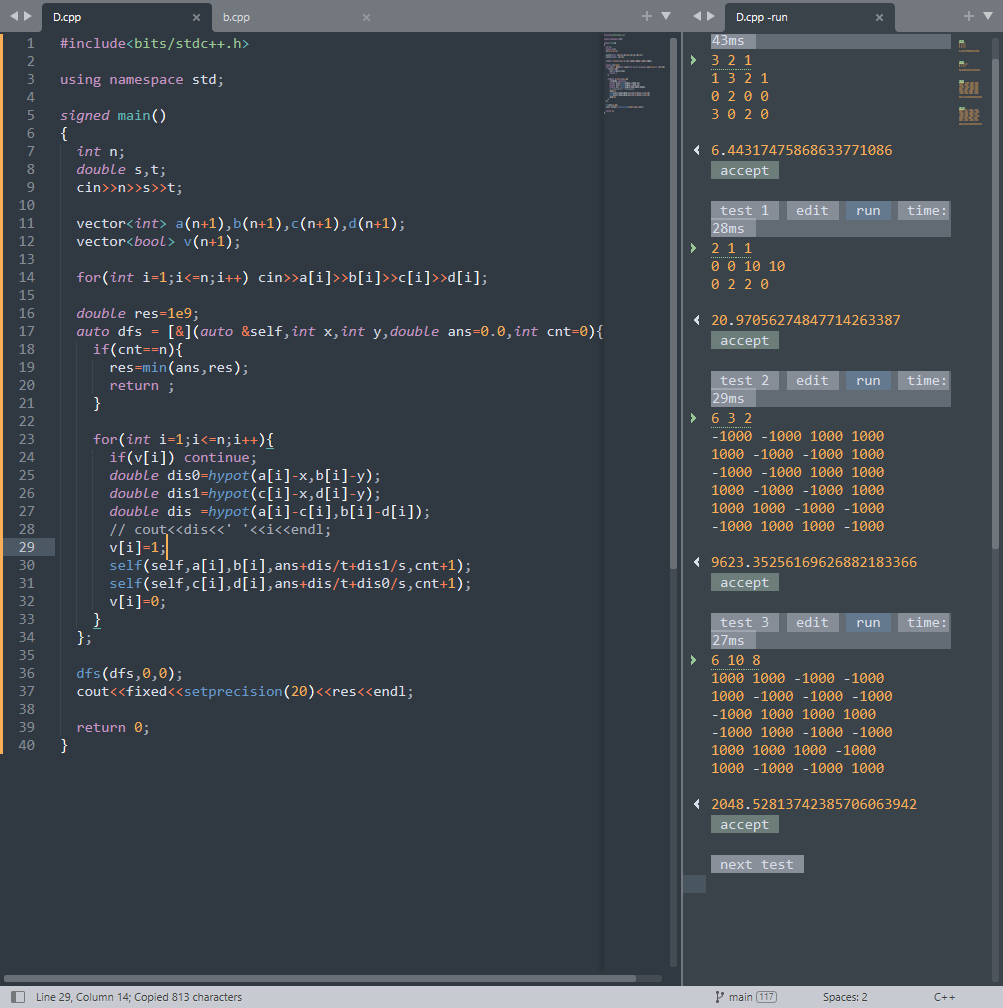
打印开始,坐标位于0,0.。。。。。。。。
佩服,我是理解错了,如果用最小生成树,那么还得建其实坐标到所有边的两个端点的边
#include<bits/stdc++.h>using namespace std;
typedef long long ll;
const int N=10,M=2*N;
int pa[N];
int n;
double s,t;struct xian{int a,b;int c,d;double dis=0;
}xs[N];struct node{int a,b;double dis;bool operator<(const node &M)const{return dis<M.dis;}
}ns[M];double dist(double x,double y,double xx,double yy){return sqrt((x-xx)*(x-xx)+(y-yy)*(y-yy));
}int find(int x){if(x!=pa[x]) pa[x]=find(pa[x]);return pa[x];
}signed main()
{cin>>n>>s>>t;double ans=0;for(int i=1;i<=n;i++){cin>>xs[i].a>>xs[i].b>>xs[i].c>>xs[i].d;xs[i].dis=dist(xs[i].a,xs[i].b,xs[i].c,xs[i].d);ans+=xs[i].dis/t;// cout<<xs[i].a<<' '<<xs[i].b<<' '<<xs[i].c<<' '<<xs[i].d<<' '<<xs[i].dis<<endl;}
// cout<<ans<<endl;int cnt=1;for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){auto &u=xs[i],&v=xs[j];double dis=1e9;dis=min(dist(u.a,u.b,v.a,v.b),dis);dis=min(dist(u.a,u.b,v.c,v.d),dis);dis=min(dist(u.c,u.d,v.a,v.b),dis);dis=min(dist(u.c,u.d,v.c,v.d),dis);ns[cnt++]={i,j,dis};}}for(int i=1;i<=n;i++){auto &u = xs[i];double dis=1e9;dis=min(dis,dist(u.a,u.b,0,0));dis=min(dis,dist(u.c,u.d,0,0));ns[cnt++]={0,i,dis};}sort(ns+1,ns+cnt+1);for(int i=1;i<=n;i++) pa[i]=i;for(int i=1;i<=cnt;i++){int a=ns[i].a;int b=ns[i].b;double dis=ns[i].dis;a=find(a),b=find(b);if(a!=b){// cout<<a<<' '<<b<<' '<<dis<<endl; pa[a]=b;ans+=dis/s;}}printf("%lf",ans);return 0;
}

样例2,还是不行,因为对于0到其他的点,不可能再从0出发,那样会浪费时间
还是老老实实的搜索吧
#include<bits/stdc++.h>using namespace std;signed main()
{int n,s,t;cin>>n>>s>>t;vector<int> a(n+1),b(n+1),c(n+1),d(n+1);vector<bool> v(n+1);for(int i=1;i<=n;i++) cin>>a[i]>>b[i]>>c[i]>>d[i];double res=1e9;auto dfs = [&](auto &self,int x,int y,double ans=0.0,int cnt=0){if(cnt==n){res=min(ans,res);return ;}for(int i=1;i<=n;i++){if(v[i]) continue;double dis0=hypot(a[i]-x,b[i]-y);double dis1=hypot(c[i]-x,b[i]-y);double dis =hypot(a[i]-c[i],b[i]-d[i]);cout<<dis<<endl;v[i]=1;self(self,a[i],b[i],ans+dis,cnt+1);self(self,c[i],d[i],ans+dis,cnt+1);v[i]=0;}};dfs(dfs,0,0);return 0;
}
正解
学会用sublime简直是令人赏心悦目
#include<bits/stdc++.h>using namespace std;signed main()
{int n;double s,t;cin>>n>>s>>t;vector<int> a(n+1),b(n+1),c(n+1),d(n+1);vector<bool> v(n+1);for(int i=1;i<=n;i++) cin>>a[i]>>b[i]>>c[i]>>d[i];double res=1e9;auto dfs = [&](auto &self,int x,int y,double ans=0.0,int cnt=0){if(cnt==n){res=min(ans,res);return ;}for(int i=1;i<=n;i++){if(v[i]) continue;double dis0=hypot(a[i]-x,b[i]-y);double dis1=hypot(c[i]-x,d[i]-y);double dis =hypot(a[i]-c[i],b[i]-d[i]);// cout<<dis<<' '<<i<<endl;v[i]=1;self(self,a[i],b[i],ans+dis/t+dis1/s,cnt+1);self(self,c[i],d[i],ans+dis/t+dis0/s,cnt+1);v[i]=0;}};dfs(dfs,0,0);cout<<fixed<<setprecision(20)<<res<<endl;return 0;
}
E
赛时连看都没有机会看
简单读了题目之后,是求最大值
关于生产力的定义是,每道工序在哪一天可以加工的最少产品
不知道怎么个搜法
因为如果像上一题一样有不同的线段,这一题则是有不同的商品,但是每个商品可以选择的个数不定受限制于总预算X
#include<bits/stdc++.h>using namespace std;signed main()
{return 0;
}
jiangly用到了二分答案的做法,关于上面的问题,因为能处理的数量不超过100
所以直接枚举数量到100,计算所产生的总成本,如果成本不超过二分的那个值,那么就可以计算出最小生产力
讲解得还不错的视频
#include<bits/stdc++.h>using namespace std;
typedef long long ll;signed main()
{ios::sync_with_stdio(false);cin.tie(0);int n;ll x;cin>>n>>x;vector<int> a(n+1),p(n+1),b(n+1),q(n+1);// for(int i=1;i<=n;i++) cin>>a[i]>>p[i]>>b[i]>>q[i];for(int i=1;i<=n;i++){cin>>a[i]>>p[i]>>b[i]>>q[i];if(a[i]*q[i]<b[i]*p[i]){swap(a[i],b[i]);swap(q[i],p[i]);}}auto check = [&](int mid){ll ans = 0;for(int i=1;i<=n;i++){ll res = 1e18;for(int j=0;j<=100;j++){ll need = mid-b[i]*j;// mid-=b[i]*j;// 不能直接改变目标生产力// 因为要找到需要最合适的性价比低的物品的数量ll v=j*q[i];if(mid>0){v+=(1ll)*(need+a[i]-1)/a[i]*p[i];}res=min(res,v);}ans+=res;}return ans<=x;};ll l=0,r=1e9;// 这样还不会爆intwhile(l<r){ll mid=(l+r+1)>>1;if(check(mid)) l=mid;else r=mid-1;}cout<<r<<endl;return 0;
}
是有一点背包的感觉,还没有看官方题解
官方题解也是枚举+二分答案
相关文章:

atcoder-374(a-e)
atcoder-374 文章目录 atcoder-374ABC简洁的写法正解 D正解 E A #include<bits/stdc.h>using namespace std;signed main() {string s;cin>>s;string strs.substr(s.size()-3);if(str "san") puts("Yes");else puts("No");return 0…...
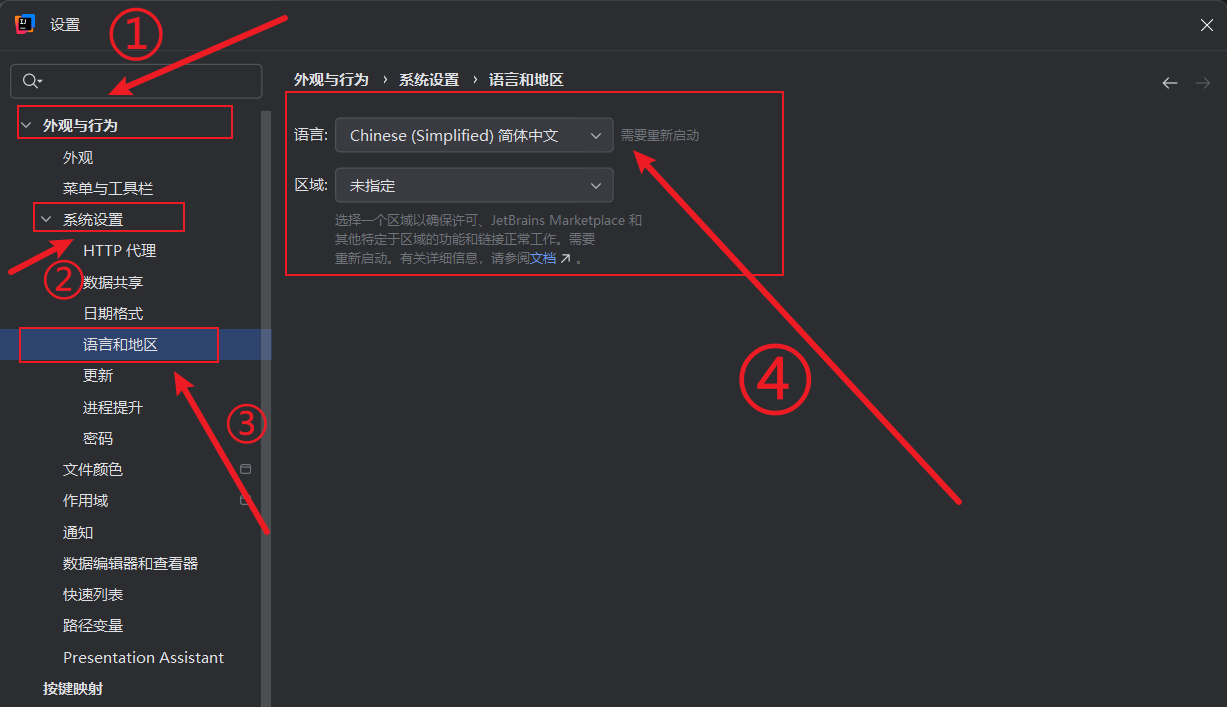
idea2024设置中文
今天下载idea2024.2版本,发现已经装过中文插件,但是还是不显示中文,找了半天原来还需要设置中文选项 方案一 点击文件 -> 关闭项目 点击自定义 -> 选择语言 方案二 点击文件 -> 设置 外观与行为 -> 系统设置 -> 语言和地区…...

跨境电商独立站轮询收款问题
想必做跨境电商独立站的小伙伴,对于PayPal是再熟悉不过了,PayPal是一个跨国际贸易的支付平台,对于做独立站的朋友来说跨境收款绝大部分都是依赖PayPal以及Stripe条纹了。简单来说PayPal跟国内的支付宝有点类似,但是PayPal它是跨国…...

[OS] 3.Insert and Remove Kernel Module
Insert and Remove Kernel Module 1. 切换到 root 账户 $ sudo su作用:Linux 内核模块的加载和卸载需要超级用户权限,因此你必须以 root 用户身份进行操作。sudo su 命令允许你从普通用户切换到 root 账户,从而获得系统的最高权限ÿ…...

updatedb命令:更新locate数据库
一、命令简介 updatedb 命令用于更新 locate 命令使用的文件数据库,以便 locate 命令能够快速定位文件。 二、命令参数 命令格式 updatedb [选项]选项 -l: 仅更新本地文件系统(默认行为)-U: 更新所有文件系统-o D…...

分布式共识算法ZAB
文章目录 概述一、ZAB算法概述二、ZAB算法的核心特性三、ZAB算法的工作流程四、ZAB算法的优势与局限 其他共识算法 概述 分布式共识算法ZAB,全称Zookeeper Atomic Broadcast(Zookeeper原子广播),是Zookeeper保证数据一致性的核心…...

程序化交易与非程序化交易者盈利能力孰优孰劣
炒股自动化:申请官方API接口,散户也可以 python炒股自动化(0),申请券商API接口 python炒股自动化(1),量化交易接口区别 Python炒股自动化(2):获取…...

【JavaEE】【多线程】进程与线程的概念
目录 进程系统管理进程系统操作进程进程控制块PCB关键属性cpu对进程的操作进程调度 线程线程与进程线程资源分配线程调度 线程与进程区别线程简单操作代码创建线程查看线程 进程 进程是操作系统对一个正在运行的程序的一种抽象,可以把进程看做程序的一次运行过程&a…...
)
LeetCode hot100---贪心算法专题(C++语言)
贪心算法 当前取最优,最终完成全局最优1、买卖股票的最佳时机 (1)题目描述以及输入输出 (1)题目描述: 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。(2)输入输出描述: 输入&…...

《PyTorch深度学习快速入门教程》学习笔记(第15周)
目录 摘要 Abstract 1. 安装Anaconda 2. 查看显卡驱动 3. 安装Pytorch 4. Pytorch加载数据 5. 常用数据集两种形式 6. 路径直接加载数据 7. Dataset加载数据 摘要 本周报的目的在于汇报《PyTorch深度学习快速入门教程》课程第一周的学习成果,主要聚焦于py…...
)
kubeadm部署k8s1.28.0主从集群(cri-dockerd)
1. kubernetes集群规划 主机IP主机名主机配置角色192.168.100.3master12C/4G管理节点192.168.100.4node12C/4G工作节点192.168.100.5node22C/4G工作节点 2. 集群前期环境准备 (1)初始化脚本 #!/bin/bash echo "——>>> 关闭防火墙与SE…...

C语言复习概要(四)
本文 1. 操作符的分类算术操作符关系操作符逻辑操作符 2. 二进制制和进制转换二进制与十六进制的表示进制转换算法 3. 原码、反码和补码原码反码补码 1. 操作符的分类 C语言中的操作符种类繁多,常用的主要操作符可以按照其功能进行如下分类: 算术操作符…...

【楚怡杯】职业院校技能大赛 “Python程序开发”数据清洗练习
题目: 将书名为‘一级建造师 2020教材 2020版一级建造师 建筑工程管理与实务’的作者(空值)改为 全国一级建造师执业资格考试用书编写委员会,‘出版日期’改为‘2020-05-01’将书名为‘中国共产党简史(32开࿰…...
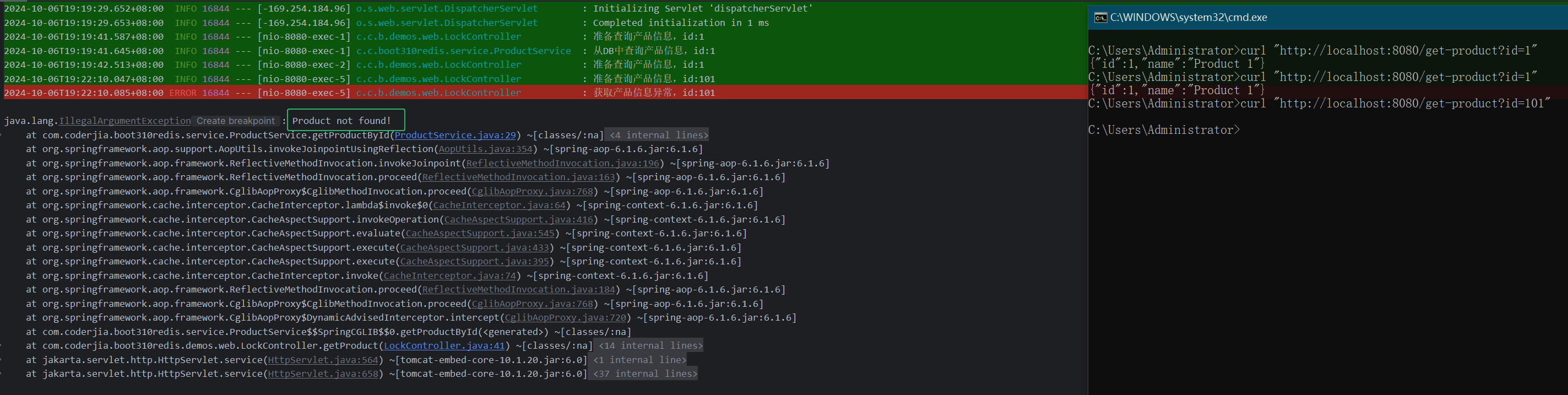
重学SpringBoot3-集成Redis(五)之布隆过滤器
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 重学SpringBoot3-集成Redis(五)之布隆过滤器 1. 什么是布隆过滤器?基本概念适用场景 2. 使用 Redis 实现布隆过滤器项目依赖Redis 配置…...

BGP路由原理详解
🐣个人主页 可惜已不在 🐤这篇在这个专栏 华为_可惜已不在的博客-CSDN博客 🐥有用的话就留下一个三连吧😼 目录 一. BGP简介: 二. BGP报文中的角色 BGP的报文 BGP处理过程 BGP有限状态机 BGP属性 三. BGP作用 四. BGP选路 …...

Pytorch实现心跳信号分类识别(支持LSTM,GRU,TCN模型)
Pytorch实现心跳信号分类识别(支持LSTM,GRU,TCN模型) 目录 Pytorch实现心跳信号分类识别(支持LSTM,GRU,TCN模型) 1. 项目说明 2. 数据说明 (1)心跳信号分类预测数据集 3. 模型训练 (1)项目安装 &am…...

AI股市预测的可参考价值有几何?
1. AI技术在股市预测中的应用 首先,AI技术在股市预测中的应用主要包括机器学习、深度学习、自然语言处理(NLP)和量化金融模型等。机器学习算法能够处理和分析大量的金融数据,从中寻找模式和规律。而深度学习特别是在处理复杂的非线…...

【大数据应用开发】2023年全国职业院校技能大赛赛题第02套
需要技能竞赛软件测试资料的同学们可s聊我,详细了解 目录 任务A:大数据平台搭建(容器环境)(15分) 任务B:离线数据处理(25分 任务C:数据挖掘(10分…...

2. 将GitHub上的开源项目导入(clone)到(Linux)服务器上——深度学习·科研实践·从0到1
目录 1. 在github上搜项目 (以OpenOcc为例) 2. 转移到码云Gitee上 3. 进入Linux服务器终端 (jupyter lab) 4. 常用Linux命令 5. 进入对应文件夹中导入项目(代码) 注意:系统盘和数据盘 1. 在github上搜项目 (以OpenOcc为例) 把链接复制下…...

毕业设计项目——基于transformer的中文医疗领域命名实体识别(论文/代码)
完整的论文代码见文章末尾 以下为核心内容 摘要 近年来,随着深度学习技术的发展,基于Transformer和BERT的模型在自然语言处理领域取得了显著进展。在中文医疗领域,命名实体识别(Named Entity Recognition, NER)是一项重要任务,旨…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
