C语言复习概要(四)

本文
- 1. 操作符的分类
- 算术操作符
- 关系操作符
- 逻辑操作符
- 2. 二进制制和进制转换
- 二进制与十六进制的表示
- 进制转换算法
- 3. 原码、反码和补码
- 原码
- 反码
- 补码
1. 操作符的分类
C语言中的操作符种类繁多,常用的主要操作符可以按照其功能进行如下分类:
- 算术操作符:用于基本的数学运算,例如加法、减法、乘法和除法。
- 关系操作符:用于比较两个操作数的关系,返回布尔值(真或假)。
- 逻辑操作符:用于逻辑运算,如与、或、非等,用于条件判断。
- 位操作符:按位操作符处理位级别的数据操作。
- 赋值操作符:将右侧的值赋给左侧变量。
- 条件操作符(三元运算符):对条件表达式进行判断,并根据条件返回不同的值。
- 逗号操作符:顺序执行多个表达式,并返回最后一个表达式的值。
- 其他操作符:包括取地址符号
&、指针解引用符*等。
算术操作符
算术操作符用于处理整数和浮点数的基本运算,它们包括加法(+)、减法(-)、乘法(*)、除法(/)和取模(%)。
代码示例:更复杂的算术操作
#include <stdio.h>int main() {int a = 15, b = 4;float x = 7.5, y = 2.0;// 整数算术操作printf("a + b = %d\n", a + b); // 加法printf("a - b = %d\n", a - b); // 减法printf("a * b = %d\n", a * b); // 乘法printf("a / b = %d\n", a / b); // 整数除法printf("a %% b = %d\n", a % b); // 取模操作// 浮点数算术操作printf("x + y = %.2f\n", x + y); // 浮点加法printf("x - y = %.2f\n", x - y); // 浮点减法printf("x * y = %.2f\n", x * y); // 浮点乘法printf("x / y = %.2f\n", x / y); // 浮点除法// 混合算术操作printf("a + x = %.2f\n", a + x); // 整数与浮点混合运算printf("b * y = %.2f\n", b * y);return 0;
}
在这个例子中,我们展示了整数与浮点数的加法、减法、乘法、除法和取模运算。整数运算和浮点数运算的区别是,整数除法会丢弃小数部分,而浮点运算会保留小数部分。
关系操作符
关系操作符用于比较两个值,并返回一个布尔结果。它们包括:
==:等于。!=:不等于。<:小于。>:大于。<=:小于等于。>=:大于等于。
代码示例:使用关系操作符进行比较
#include <stdio.h>int main() {int a = 10, b = 20;// 比较 a 和 bif (a == b) {printf("a 等于 b\n");} else {printf("a 不等于 b\n");}if (a < b) {printf("a 小于 b\n");} else {printf("a 不小于 b\n");}if (a >= 5) {printf("a 大于等于 5\n");}return 0;
}
通过使用关系操作符,可以轻松判断两个操作数之间的大小关系,从而在程序中做出条件判断。关系操作符的返回结果通常用于if语句或其他控制结构中。
逻辑操作符
逻辑操作符用于布尔逻辑运算,包括:
&&:逻辑与。如果两个操作数都为真,则结果为真。||:逻辑或。如果至少一个操作数为真,则结果为真。!:逻辑非。将真值转换为假,将假值转换为真。
代码示例:逻辑操作符在条件判断中的使用
#include <stdio.h>int main() {int a = 5, b = 10, c = 15;// 使用逻辑与操作符if (a < b && b < c) {printf("a 小于 b 且 b 小于 c\n");}// 使用逻辑或操作符if (a > b || b < c) {printf("a 大于 b 或者 b 小于 c\n");}// 使用逻辑非操作符if (!(a == b)) {printf("a 不等于 b\n");}return 0;
}
在这个示例中,逻辑与(&&)和逻辑或(||)用于复杂条件判断。逻辑非(!)通常用于反转条件的布尔值,便于简化条件表达式。
2. 二进制制和进制转换
二进制(binary)、八进制(octal)和十六进制(hexadecimal)在低层次的系统编程中非常常见。C语言提供了便捷的方法来表示不同进制的数值。理解二进制数对于掌握位操作符至关重要,而进制转换则是在二进制、十进制和十六进制之间切换。
二进制与十六进制的表示
在C语言中,二进制数通常以0b开头表示,而十六进制数则以0x开头表示。例如,0b1010代表二进制的数字10,而0xA表示十六进制的数字10。
代码示例:二进制、八进制和十六进制表示法
#include <stdio.h>int main() {int binaryNum = 0b1010; // 二进制 1010, 等于十进制 10int octalNum = 012; // 八进制 12, 等于十进制 10int hexNum = 0xA; // 十六进制 A, 等于十进制 10printf("二进制数 0b1010 = %d\n", binaryNum);printf("八进制数 012 = %d\n", octalNum);printf("十六进制数 0xA = %d\n", hexNum);return 0;
}
在上述代码中,我们使用了不同的进制表示方法,展示了如何在C语言中处理各种进制表示。printf函数中的%d会将数值转换为十进制输出。
进制转换算法
在实际开发中,我们经常需要将一个进制数转换为另一个进制数。下面我们展示如何手动实现二进制到十进制的转换。
代码示例:手动实现进制转换
#include <stdio.h>
#include <math.h>// 二进制转换为十进制
int binaryToDecimal(int binary) {int decimal = 0, i = 0, remainder;while (binary != 0) {remainder = binary % 10;binary /= 10;decimal += remainder * pow(2, i);++i;}return decimal;
}// 十进制转换为二进制
int decimalToBinary(int decimal) {int binary = 0, i = 1, remainder;while (decimal != 0) {remainder = decimal % 2;decimal /= 2;binary += remainder * i;i *= 10;}return binary;
}int main() {int binary = 1010;int decimal = 10;printf("二进制 %d 转换为十进制: %d\n", binary, binaryToDecimal(binary));printf("十进制 %d 转换为二进制: %d\n", decimal, decimalToBinary(decimal));return 0;
}
这个例子展示了如何手动将二进制转换为十进制,反之亦然。通过简单的算法,可以帮助理解进制转换的过程
。
3. 原码、反码和补码
原码、反码和补码是用于表示负数的不同方法,它们在底层编程中极其重要,特别是在涉及位操作时。C语言使用补码来表示负数,这是因为它可以简化硬件加减法操作。
原码
原码是最简单的表示方法,使用符号位来区分正负号。最高位为0表示正数,为1表示负数。例如:
+5的原码是:00000101-5的原码是:10000101
反码
反码是对原码的符号位保持不变,其余位按位取反。正数的反码与原码相同,而负数的反码则是在正数基础上按位取反。例如:
+5的反码是:00000101-5的反码是:11111010
补码
补码是计算机中最常用的表示负数的方法。负数的补码是反码加1。这样可以简化硬件中的加减法操作。例如:
+5的补码是:00000101-5的补码是:11111011
代码示例:理解补码的表示
#include <stdio.h>int main() {signed char a = 5; // 原码: 00000101signed char b = -5; // 补码: 11111011printf("5 的二进制补码: %d\n", a);printf("-5 的二进制补码: %d\n", b);return 0;
}
在上面的例子中,计算机内部存储负数的方式是通过补码完成的,理解补码对于进行位操作和低级编程非常重要。
相关文章:

C语言复习概要(四)
本文 1. 操作符的分类算术操作符关系操作符逻辑操作符 2. 二进制制和进制转换二进制与十六进制的表示进制转换算法 3. 原码、反码和补码原码反码补码 1. 操作符的分类 C语言中的操作符种类繁多,常用的主要操作符可以按照其功能进行如下分类: 算术操作符…...

【楚怡杯】职业院校技能大赛 “Python程序开发”数据清洗练习
题目: 将书名为‘一级建造师 2020教材 2020版一级建造师 建筑工程管理与实务’的作者(空值)改为 全国一级建造师执业资格考试用书编写委员会,‘出版日期’改为‘2020-05-01’将书名为‘中国共产党简史(32开࿰…...
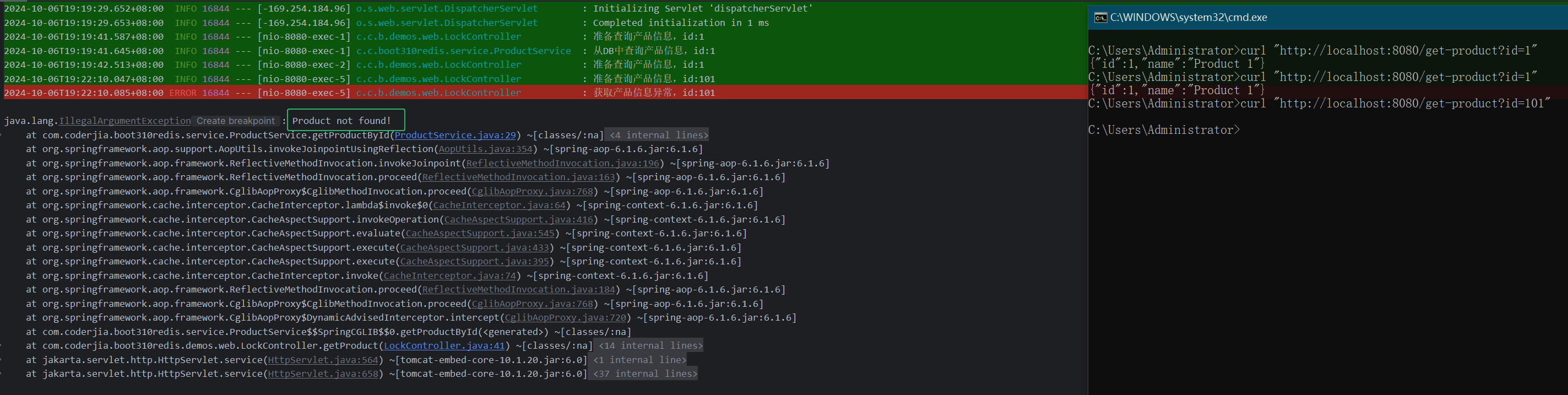
重学SpringBoot3-集成Redis(五)之布隆过滤器
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 重学SpringBoot3-集成Redis(五)之布隆过滤器 1. 什么是布隆过滤器?基本概念适用场景 2. 使用 Redis 实现布隆过滤器项目依赖Redis 配置…...

BGP路由原理详解
🐣个人主页 可惜已不在 🐤这篇在这个专栏 华为_可惜已不在的博客-CSDN博客 🐥有用的话就留下一个三连吧😼 目录 一. BGP简介: 二. BGP报文中的角色 BGP的报文 BGP处理过程 BGP有限状态机 BGP属性 三. BGP作用 四. BGP选路 …...

Pytorch实现心跳信号分类识别(支持LSTM,GRU,TCN模型)
Pytorch实现心跳信号分类识别(支持LSTM,GRU,TCN模型) 目录 Pytorch实现心跳信号分类识别(支持LSTM,GRU,TCN模型) 1. 项目说明 2. 数据说明 (1)心跳信号分类预测数据集 3. 模型训练 (1)项目安装 &am…...

AI股市预测的可参考价值有几何?
1. AI技术在股市预测中的应用 首先,AI技术在股市预测中的应用主要包括机器学习、深度学习、自然语言处理(NLP)和量化金融模型等。机器学习算法能够处理和分析大量的金融数据,从中寻找模式和规律。而深度学习特别是在处理复杂的非线…...

【大数据应用开发】2023年全国职业院校技能大赛赛题第02套
需要技能竞赛软件测试资料的同学们可s聊我,详细了解 目录 任务A:大数据平台搭建(容器环境)(15分) 任务B:离线数据处理(25分 任务C:数据挖掘(10分…...

2. 将GitHub上的开源项目导入(clone)到(Linux)服务器上——深度学习·科研实践·从0到1
目录 1. 在github上搜项目 (以OpenOcc为例) 2. 转移到码云Gitee上 3. 进入Linux服务器终端 (jupyter lab) 4. 常用Linux命令 5. 进入对应文件夹中导入项目(代码) 注意:系统盘和数据盘 1. 在github上搜项目 (以OpenOcc为例) 把链接复制下…...

毕业设计项目——基于transformer的中文医疗领域命名实体识别(论文/代码)
完整的论文代码见文章末尾 以下为核心内容 摘要 近年来,随着深度学习技术的发展,基于Transformer和BERT的模型在自然语言处理领域取得了显著进展。在中文医疗领域,命名实体识别(Named Entity Recognition, NER)是一项重要任务,旨…...
)
电子信息类专业技术学习及比赛路线总结(大一到大三)
本文主要是总结到目前为止电子信息类的专业技能、比赛路线,以后会持续更新,希望能为那些热爱电子技术或渴望学习课本之外知识的小伙伴们提供帮助,参加学科竞赛和找工作必备。(毕竟很多课本上的内容都没什么用 ) 1.单片…...
的所有输出保存到log/txt中?)
怎么将bash(sh)的所有输出保存到log/txt中?
tee 命令 这会将所有输出同时显示在屏幕上并追加到日志文件中。 bash your_script.sh 2>&1 | tee -a log_file.txt 其他方法不可用 只使用 >> 不会将除了print之外的所有保存 bash your_script.sh >> log_file.txt >> 和 2>&1一起只会保存在日…...

腾讯云服务器上使用Nginx部署的静态网站打开速度慢的原因分析及优化解决方案
目录 前言1. 网站打开速度慢的原因分析1.1 服务器配置不足1.2 网络延迟1.3 Nginx配置不合理1.4 静态资源未优化 2. 网站速度的测试与分析2.1 使用浏览器开发者工具分析2.2 在线工具测试 3. 网站优化的具体方法3.1 服务器配置优化3.2 CDN加速与DNS优化3.3 优化Nginx配置3.3.1 启…...
如何移除 iPhone 上的网络锁?本文筛选了一些适合您的工具
您是否对 iPhone 运营商的网络感到困惑?不用担心,我们将向您介绍 8 大免费 iPhone 解锁服务。这些工具可以帮助您移除 iPhone 上的网络锁,并使您能够永久在网络上使用您的设备。如果您想免费解锁 iPhone,请阅读本文并找到最适合您…...

深度学习:CycleGAN图像风格迁移转换
目录 基础概念 模型工作流程 循环一致性 几个基本概念 假图像(Fake Image) 重建图像(Reconstructed Image) 身份映射图像(Identity Mapping Image) CyclyGAN损失函数 对抗损失 身份鉴别损失 Cyc…...

pytorch和yolo区别
PyTorch与YOLO的区别:一个简明的科普 在深度学习的领域,有许多工具和框架帮助研究人员和开发者快速实现复杂的模型。其中,PyTorch与YOLO(You Only Look Once)是两个非常重要的名词。本文旨在探讨这两个技术之间的区别&…...
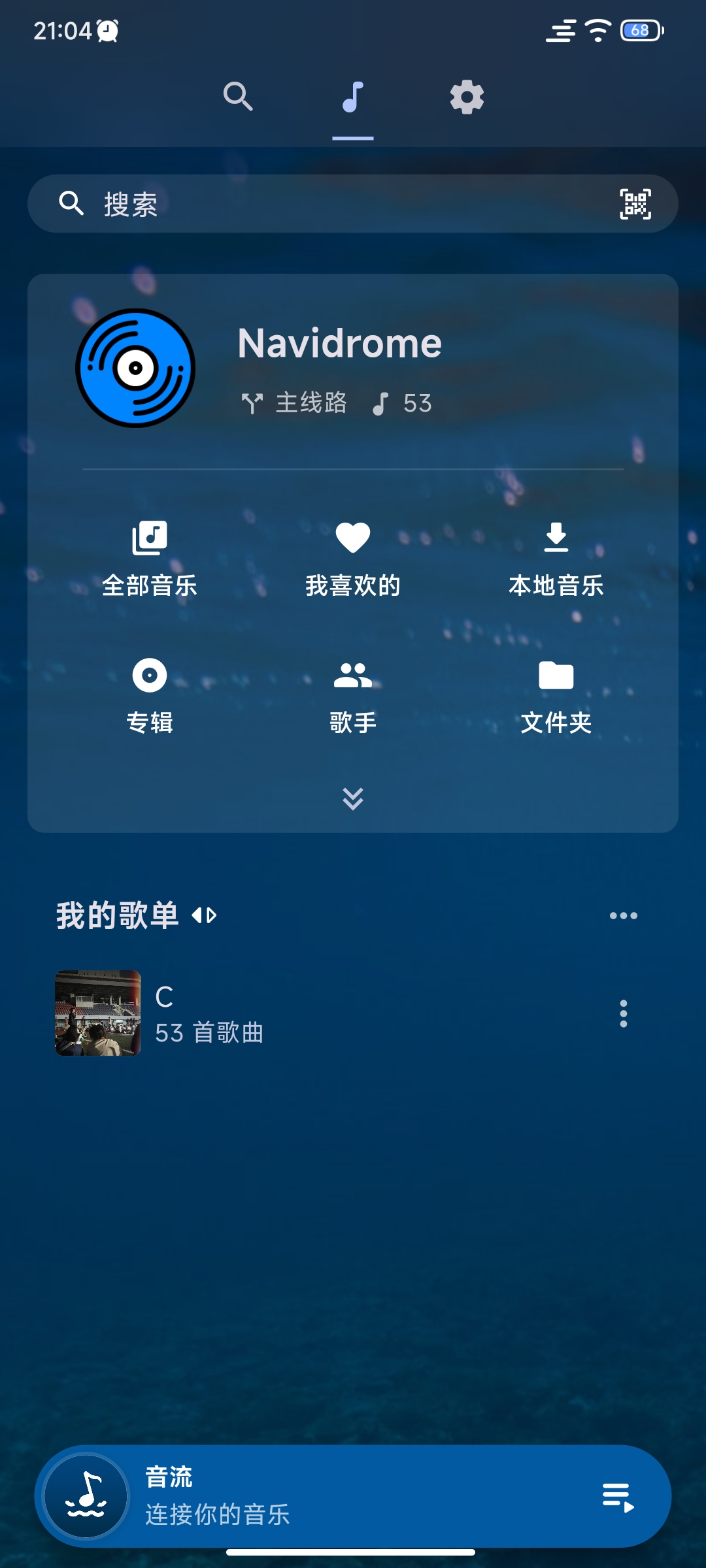
使用树莓派搭建音乐服务器
目录 引言一、搭建Navidrome二、服务穿透三、音流配置 引言 本人手机存储空间128G,网易云音乐6个G,本就不富裕的空间更是雪上加霜,而且重点是,我根本没有听几首歌,清除缓存后,整个软件都还是占用了5个G左右…...

单链表的分解
编写算法创建以整数为数据元素的单向链表,实现将其分解成两个链表,其中一个全部为奇数,另一个全部为偶数(尽量利用已知的存储空间)。 输入格式: 1 2 3 4 5 6 7 8 9 0 输出格式: 1 3 5 7 9 2 4 6 8 输入样例: …...

[OS] 4.Linux 内核
1. 下载 Linux 内核源代码 首先,你需要从官方站点或镜像站点下载 Linux 内核源代码。 官方源代码:The Linux Kernel Archives 清华大学镜像站点:Index of /kernel/v5.x/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 下载 .t…...

flutter_鸿蒙next_Dart基础③函数
目录 说在前面 1. 函数的基本定义 例子 代码解释 2. 函数的调用 代码解释 3. 可选参数与命名参数 可选参数 代码解释 调用示例 命名参数 代码解释 调用示例 4. 匿名函数与高阶函数 例子 代码解释 说在最后 说在前面 在 Dart 编程语言中,函数是构建…...

基于猎豹优化算法(The Cheetah Optimizer,CO)的多无人机协同三维路径规划(提供MATLAB代码)
一、猎豹优化算法 猎豹优化算法(The Cheetah Optimizer,CO)由MohammadAminAkbari等人于2022年提出,该算法性能高效,思路新颖。 参考文献: Akbari, M.A., Zare, M., Azizipanah-abarghooee, R. et al. The…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
