【C++】二叉搜索树+变身 = 红黑树


目录
- 前言
- 一、定义与性质
- 二、红黑树节点的定义
- 三、新增节点插入
- 四、验证红黑树
- 五、AVL树和红黑树比较
前言
本文仅适合了解二叉搜索树,但不了解红黑树底层原理的同学阅读哦。
本篇文章不会带你从头到尾实现红黑树,但会带你深入理解红黑树是怎么实现平衡的,怎么通过旋转变换实现保持平衡,以及实现平衡过程中的细节应该怎么处理等。
一、定义与性质
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。

- 根节点是黑色的
- 每个节点不是红色就是黑色
- 如果一个节点是红色的,则它的两个孩子一定是黑色的(没有连续的红色节点)
- 对每个节点,从该节点到其所有后代叶子结点的简单路径上,黑色节点数目相同
- 每个叶子节点都是黑色的(此处的叶子结点指的是空节点,通常是为了算路径)
其中第三点和第四点是控制红黑树平衡的关键,与AVL树不同的是,红黑树不再关注高度,只关注颜色,只要控制住了颜色就控制住了高度。
二、红黑树节点的定义
维持二叉搜索树的平衡,旋转处理是必要的,因此红黑树的节点也需要指向其父节点。
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv, colour col = RED):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(col){}
};
上面我们将节点的默认颜色设置为红色,为什么不是黑色呢?
新增节点默认设置为红色或黑色都可能会破坏红黑树的性质,默认为红色对红黑树的性质影响最小,就算修改也更为容易。另外红黑树主要还是以黑色节点为主,在红黑树中黑色节点通常都是通过变色而来的,而红色节点往往都是新增的。
三、新增节点插入
虽然新增节点默认为红色,但根节点必须是黑色。
bool Insert(const pair<K, V>& kv)
{Node* pcur = _root;Node* parent = nullptr;if (pcur == nullptr)//当前还没有节点{_root = new Node(kv);_root->_col = BLACK;//根节点必须是黑色的return true;}//...
}
插入一个红色节点,其父亲是红色时才需要处理, 当父亲是红色时其爷爷一定是黑色,不然在插入新节点之前红黑树就已经有问题了。
所以处理过程的关键是看叔叔,大体可以分为两种情况:
其中g表示grandfather,p表示parent,u表示uncle。a,b,c,d,e为红黑子树。
| 情况一:g为黑,p为红,u存在且为红
| 处理方法:变色,继续向上调整

上图中pcur可能为新增节点,也可能之前为黑,是经过变色而来的。
//当父节点存在且为红时需要调整
while (parent && parent->_col == RED)
{if (parent == grandfather->_left){uncle = grandfather->_right;}else{uncle = grandfather->_left;}if (uncle && uncle->_col == RED)//情况一:u存在且为红{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;if (grandfather->_parent == nullptr){grandfather->_col = BLACK;return true;}pcur = grandfather;parent = pcur->_parent;grandfather = parent->_parent;}//...
}
| 情况二:g为黑,p为红,u存在且为黑 / u不存在
| 处理方法:旋转 + 变色
单旋:

void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;subL->_right = parent;if (subLR){subLR->_parent = parent;}Node* parentparent = parent->_parent;parent->_parent = subL;if (parentparent == nullptr){_root = subL;}else{if (parent == parentparent->_left){parentparent->_left = subL;}else{parentparent->_right = subL;}}subL->_parent = parentparent;
}void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;Node* parentparent = parent->_parent;parent->_parent = subR;if (parentparent == nullptr){_root = subR;}else{if (parent == parentparent->_left){parentparent->_left = subR;}else{parentparent->_right = subR;}}subR->_parent = parentparent;
}
双旋:

//当父节点存在,且颜色为红,需要往上更新
while (parent && parent->_col == RED)
{if (parent == grandfather->_left){uncle = grandfather->_right;}else{uncle = grandfather->_left;}//情况一:u存在且为红else //情况二:u存在且为黑 / 情况三:u不存在{if (parent == grandfather->_left && pcur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else if (parent == grandfather->_left && pcur == parent->_right){RotateL(parent);RotateR(grandfather);pcur->_col = BLACK;grandfather->_col = RED;}else if (parent == grandfather->_right && pcur == parent->_left){RotateR(parent);RotateL(grandfather);pcur->_col = BLACK;grandfather->_col = RED;}else if (parent == grandfather->_right && pcur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_cocl = RED;}break;}
}
总结:
- 红黑树的插入主要以黑色节点为主,时刻维持黑色节点的数量
- 处理过程应尽量避免旋转,能变色就不旋转
- 黑色节点通常都是受限于红黑树的性质而不得不变色而来的,红色节点通常都是新增的
不管是变色还是旋转,始终都要保持插入新节点前后各路径上黑色节点的数量。
四、验证红黑树
- 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 检测其是否满足红黑树的性质
检测红黑树的性质,主要检测红黑树的根节点是否为黑色、任意一个红色节点的父节点不是红色、任意节点到根节点的路径上黑色节点的数量相等。
其中检测任意节点到根节点的路径上黑色节点数量相等可以用递归处理,先算出某条路径上黑色节点的数量,通过递归与每条路径上黑色节点的数量最对比,如果与某条路径上黑色节点的数量不相等则红黑树异常。
bool IsValidRBTree()
{Node* pRoot = _root;if (nullptr == pRoot){return true;}//检测根节点是否满足情况if (BLACK != pRoot->_col){cout << "违反性质二:根节点必须为黑色" << endl;return false;}//获取任意一条路径中黑色节点的个数size_t blackCount = 0;Node* pcur = pRoot;while (pcur){if (BLACK == pcur->_col)blackCount++;pcur = pcur->_left;}//检测是否满足红黑树的性质,k用来记录路径中黑色节点的个数size_t k = 0;return _IsValidRBTree(pRoot, k, blackCount);
}bool _IsValidRBTree(Node* pRoot, size_t k, const size_t blackCount)
{//走到nullptr后,判断k和black是否相等if (nullptr == pRoot){cout << k << endl; if (k != blackCount){cout << "违反性质四:每条路径中黑色节点的个数必须相同" << endl;return false;}return true;}//统计黑色节点的个数if (BLACK == pRoot->_col){k++;}//检测当前节点与其双亲是否都为红色Node* pParent = pRoot->_parent;if (pParent && RED == pParent->_col && RED == pRoot->_col){cout << "违反性质三:没有连在一起的红色节点" << endl;return false;}return _IsValidRBTree(pRoot->_left, k, blackCount) &&_IsValidRBTree(pRoot->_right, k, blackCount);
}
五、AVL树和红黑树比较
- 红黑树:
- 平衡机制基于颜色和一系列规则(如节点颜色、红色节点的子节点颜色、路径上黑色节点数量等)
- 允许节点之间的高度差超过1,但通过保证从根节点到叶节点的任意路径上黑色节点的数量相同来避免树的高度过大
- 在插入或删除节点时,可能需要通过变色和少量的旋转操作来维持平衡
- AVL树:
-
平衡机制基于每个节点的左子树高度和右子树高度之差
-
严格要求所有节点的平衡因子为-1、0或1,即左右子树高度差不超过1
-
在插入或删除节点时,可能需要通过多次旋转操作来维持平衡,并更新每个节点的平衡因子
-
红黑树相对AVL树并没有那么严格地要求平衡,仅通过颜色控制最长路径中节点个数不会超过最短路径节点个数的两倍就行。
当AVL树不平衡时仅通过旋转来处理,红黑树不平衡时可以变色、变色+旋转处理,显然红黑树插入、删除过程更有优势,而AVL树查找过程更有优势。而set和map底层、Linux内核等都使用红黑树实现。
本篇文章的分享就到这里了,如果您觉得在本文有所收获,还请留下您的三连支持哦~

相关文章:

【C++】二叉搜索树+变身 = 红黑树
🚀个人主页:小羊 🚀所属专栏:C 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 前言一、定义与性质二、红黑树节点的定义三、新增节点插入四、验证红黑树五、AVL树和红黑树比较 前言 本文仅适合了…...

万界星空科技MES数据集成平台
制造执行系统MES作为连接企业上层ERP系统和现场控制系统的桥梁,承担了实时数据采集、处理、分析和传递的重要任务。MES数据集成平台是一个集成各类数据源,将数据进行整合和统一管理的系统,通过提供标准化接口和协议,实现数据的无缝…...

Ajax和axios简单用法
Ajax Ajax(Asynchronous JavaScript And XML,异步的JavaScript和XML)。 作用是: 数据交换:通过Ajax可以给服务器发送请求,并获取服务器响应的数据。异步交互:可以在不重新加载整个页面的情况…...

Chillax2024.08.01 |免费的白噪音软件
支持多种声音叠加,单独调整音量,定时功能,完全免费。 大小:13.5M 百度网盘:https://pan.baidu.com/s/1dWpdYoO1bPCnHR1bXpTZEg?pwdolxt 夸克网盘:https://pan.quark.cn/s/89dc88c56e26 移动网盘ÿ…...

Python自动化办公:从Excel到PDF生成的全流程
解锁Python编程的无限可能:《奇妙的Python》带你漫游代码世界 在现代办公环境中,数据处理和报表生成是日常工作中非常重要的一环。Python作为一门灵活且功能强大的编程语言,能够通过一系列开源库实现办公自动化。本文将详细讲解如何使用Python实现从Excel数据处理到生成PDF…...

allegro 不同页面相同网路的连接
一、cadence学习笔记(1)-原理图库制作 绘制好各个界面 放置OFFPAGE 绘制好单个界面是这个样子的,并将剩下的界面进行相同的操作 所有界面完成后,进入设计界面 右键design1.dsn选择Annotate… 点击OK后可以看到WiFi界面OFFPAGE旁边…...

医院管理新趋势:Spring Boot技术引领
4系统概要设计 4.1概述 本系统采用B/S结构(Browser/Server,浏览器/服务器结构)和基于Web服务两种模式,是一个适用于Internet环境下的模型结构。只要用户能连上Internet,便可以在任何时间、任何地点使用。系统工作原理图如图4-1所示: 图4-1系统工作原理…...

Java 新手教程!面向对象设计一口气讲完![]~( ̄▽ ̄)~*(中)
目录 Java 内部类 Java面向对象的设计 - Java 内部类 什么是内部类? 例子 使用内部类的优点 访问局部变量的限制 内部类和继承 内部类中没有静态成员 生成的内部类的类文件 静态上下文中的内类 Java 内部类类型 Java面向对象设计 - Java内部类类型 成员内…...

驰骋低代码功能升级 - 实体功能权限控制
1. 权限控制升级概述 新增功能:对新建、保存、删除、归档、撤销归档等操作的按钮进行精细化的权限控制。展示位置:这些权限控制体现在查询页面和实体卡片页面的工具栏按钮上。 2. 权限控制方式 新建 0. 不控制:任何人都可以新建。1. 指定岗…...
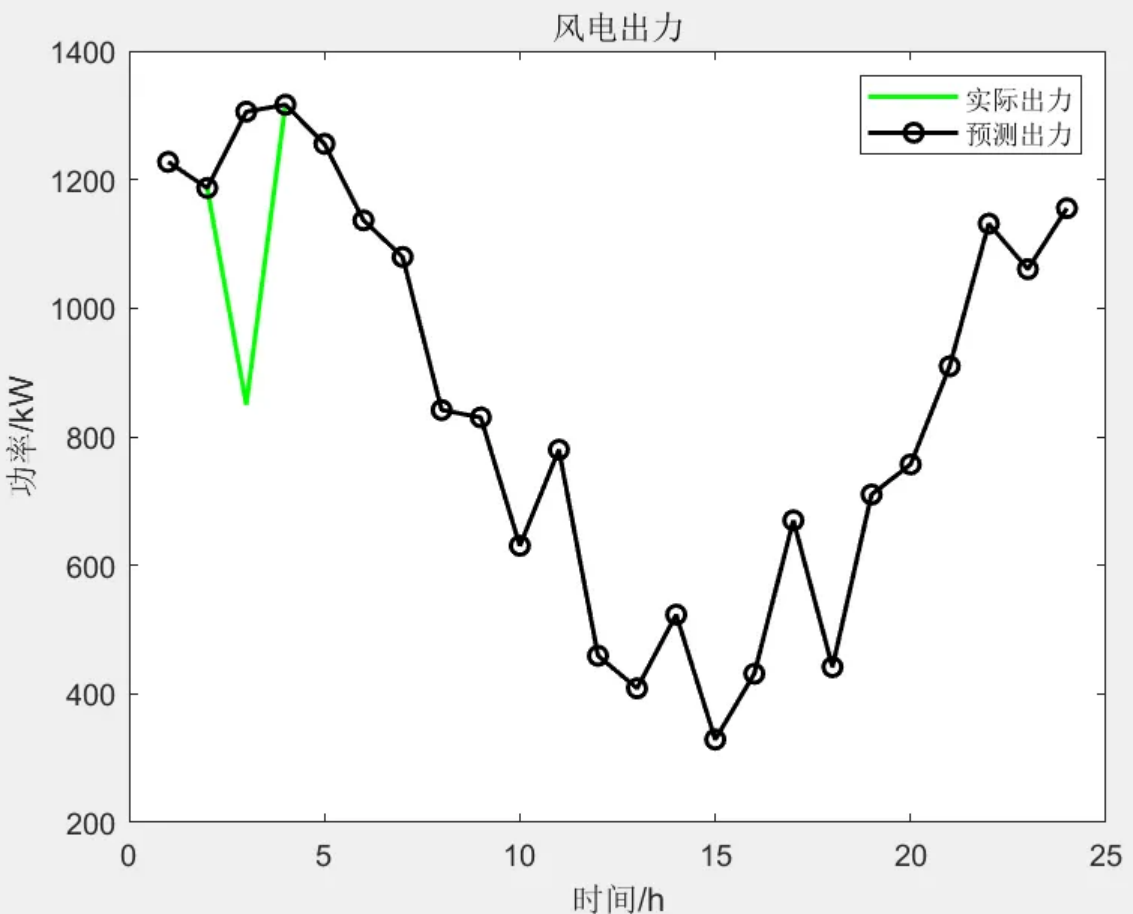
Matlab|考虑阶梯式碳交易机制与电制氢的综合能源系统热电优化
目录 1 主要内容 2 部分程序 3 程序结果 4 下载链接 1 主要内容 该程序复现《考虑阶梯式碳交易机制与电制氢的综合能源系统热电优化》,主要内容:“双碳”背景下,为提高能源利用率,优化设备的运行灵活性,进一步降低…...

Midjourney零基础学习
Midjourney学习笔记TOP01 什么是AI艺术 AI艺术指的是使用AI技术创作的艺术作品,包括AI诗歌、AI音乐、AI绘画等多种艺术表现形式;AI艺术可以被视为计算机程序与人类合作创作作品;除了Midjourney,比较流行的AI图像生成工具还有Stab…...
之Word2Vec、GloVe、FastText)
词嵌入(Word Embedding)之Word2Vec、GloVe、FastText
简介:个人学习分享,如有错误,欢迎批评指正。 词嵌入(Word Embedding)是一种将词语映射到低维稠密向量空间的技术,能够捕捉词与词之间的语义关系。Word2Vec、GloVe、FastText 是常见的词嵌入方法,…...

Vue82 路由器的两种工作模式 以及 node express 部署前端
笔记 对于一个url来说,什么是hash值?—— #及其后面的内容就是hash值。hash值不会包含在 HTTP 请求中,即:hash值不会带给服务器。hash模式: 地址中永远带着#号,不美观 。若以后将地址通过第三方手机app分享…...
[C#]使用纯opencvsharp部署yolov11-onnx图像分类模型
【官方框架地址】 https://github.com/ultralytics/ultralytics.git 【算法介绍】 使用纯OpenCvSharp部署YOLOv11-ONNX图像分类模型是一项复杂的任务,但可以通过以下步骤实现: 准备环境:首先,确保开发环境已安装OpenCvSharp和必…...

【机器学习-无监督学习】概率图模型
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈Python机器学习 ⌋ ⌋ ⌋ 机器学习是一门人工智能的分支学科,通过算法和模型让计算机从数据中学习,进行模型训练和优化,做出预测、分类和决策支持。Python成为机器学习的首选语言,…...

每日学习一个数据结构-AVL树
文章目录 概述一、定义与特性二、平衡因子三、基本操作四、旋转操作五、应用场景 Java代码实现 概述 AVL树是一种自平衡的二叉查找树,由两位俄罗斯数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明。想了解树的相关概念,请点击这里。以下是对AVL树的…...
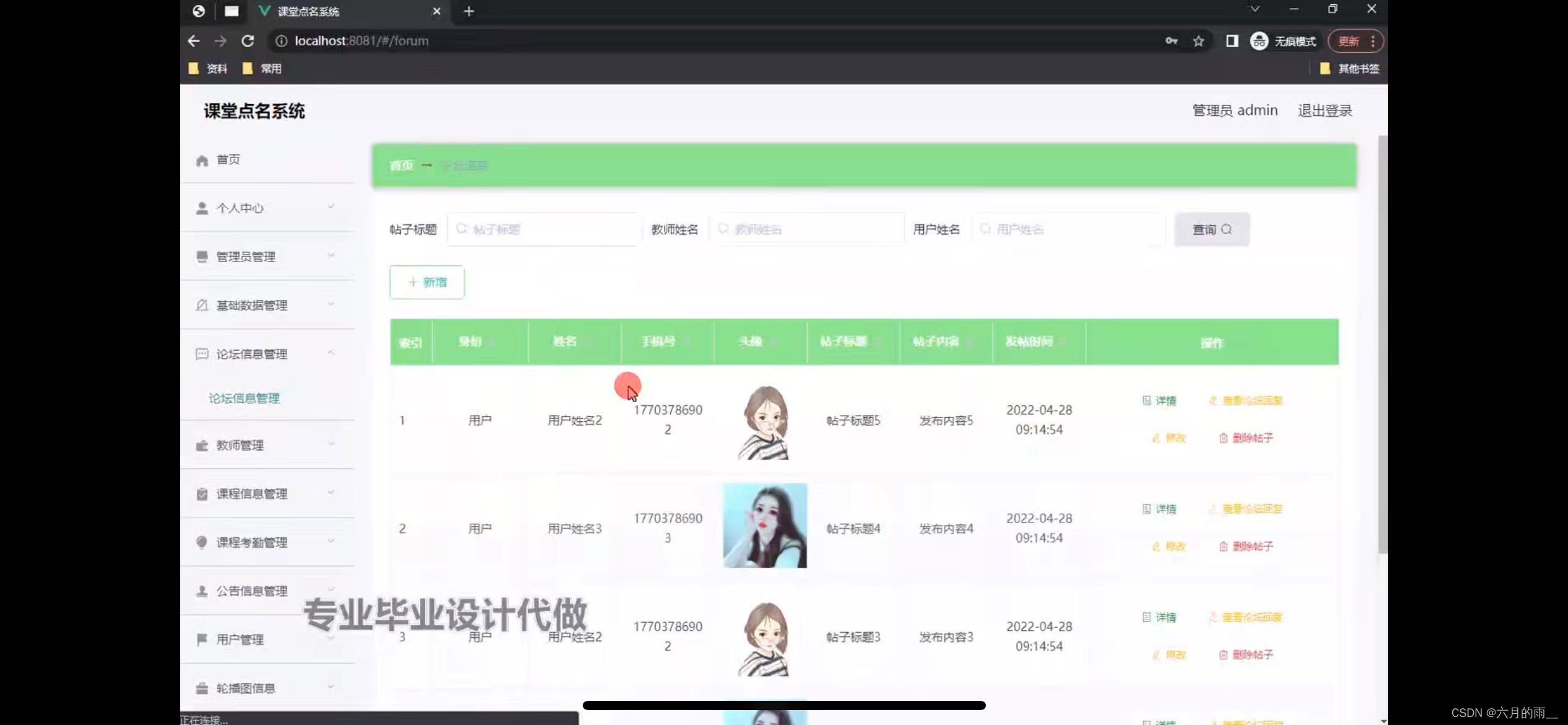
课堂点名系统小程序的设计
管理员账户功能包括:系统首页,个人中心,管理员管理,论坛信息管理,基础数据管理,课程信息管理,课程考勤管理,轮播图信息 微信端账号功能包括:系统首页,论坛信…...
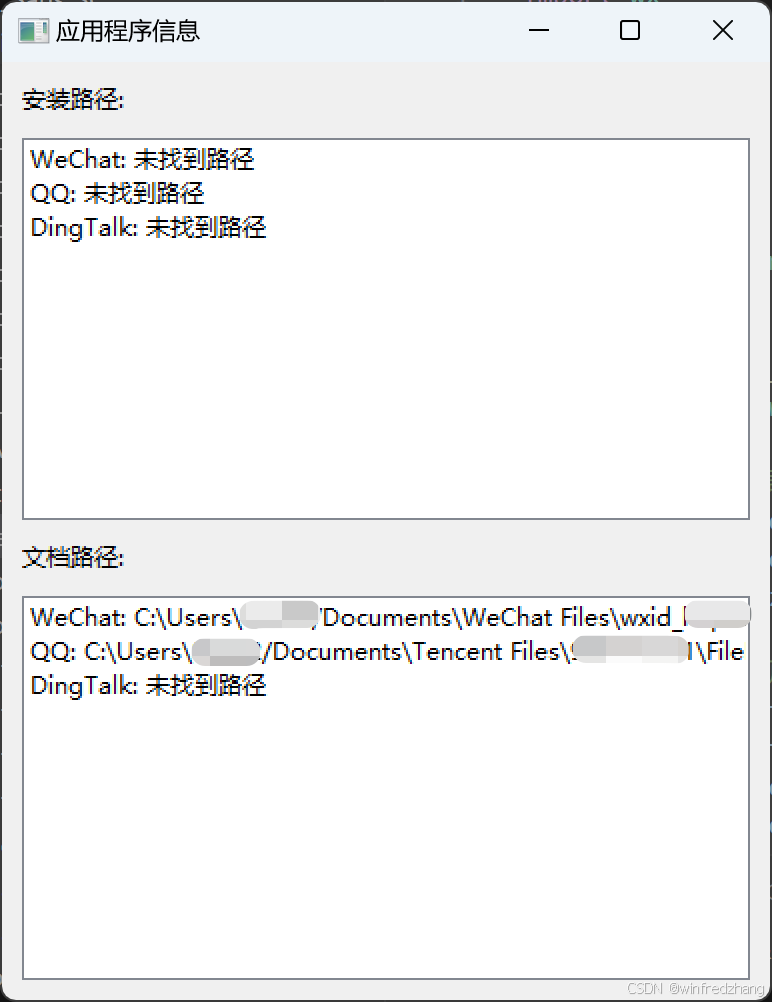
使用Python查找WeChat和QQ的安装路径和文档路径
在日常工作和生活中,我们经常需要查找某些应用程序的安装位置或者它们存储文件的位置。特别是对于像WeChat(微信)和QQ这样的即时通讯软件,了解它们的文件存储位置可以帮助我们更好地管理我们的聊天记录和共享文件。今天࿰…...

【AI大模型】深入Transformer架构:编码器部分的实现与解析(下)
目录 🍔 编码器介绍 🍔 前馈全连接层 2.1 前馈全连接层 2.2 前馈全连接层的代码分析 2.3 前馈全连接层总结 🍔 规范化层 3.1 规范化层的作用 3.2 规范化层的代码实现 3.3 规范化层总结 🍔 子层连接结构 4.1 子层连接结…...

【数据结构】【栈】算法汇总
一、顺序栈的操作 1.准备工作 #define STACK_INIT_SIZE 100 #define STACKINCREMENT 10 typedef struct{SElemType*base;SElemType*top;int stacksize; }SqStack; 2.栈的初始化 Status InitStack(SqStack &S){S.base(SElemType*)malloc(MAXSIZE*sizeof(SElemType));if(…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
